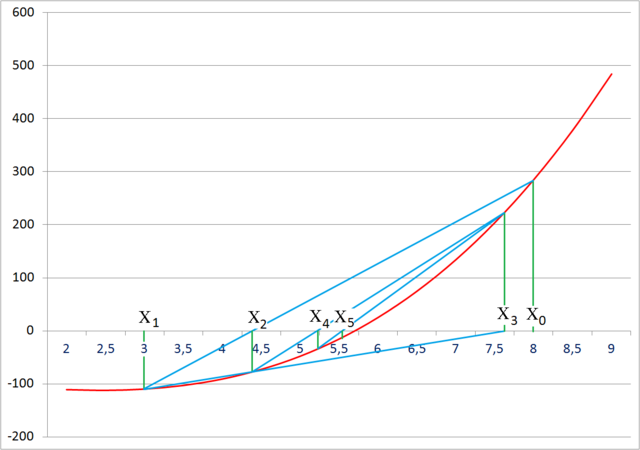
Найти корень уравнения методом секущих онлайн (2 видео)

Метод секущих

Метод секущих — итерационный численный метод приближённого нахождения корня уравнения.

Немного теории о методе секущих под калькулятором.

Содержание

Метод секущих
Метод секущих
Метод Ньютона онлайн
Другие полезные разделы:
Оставить свой комментарий:
Найти корень уравнения методом секущих онлайн
📸 Видео

Метод секущих

Метод секущих — модификация метода Ньютона, в котором производная (вычислять ее не всегда удобно) заменена на секущую.
Секущая — прямая, проходящая через две точки на графике функции. В данном методе процесс итераций состоит в том, что в качестве приближений корню уравнения принимаются последовательные значения точек пересечения секущей с осью абсцисс.

Положим, что у нас есть две точки, x0 и x1, в которых значения функции равны соответственно f(x0) и f(x1). Тогда уравнение прямой, проходящей через эти точки, будет

Для точки пересечения с осью абсцисс (у=0) получим уравнение

Это и есть наша итерационная формула. Графическое отображение метода — на рисунке ниже.

Метод работает и в случае, если начальные точки выбраны по одну и ту же сторону от корня (то есть, корня нет на отрезке между начальными приближениями), но при этом возможны случаи, когда метод не сходится.

Метод секущих является двухшаговым, то есть, новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.

В качестве критерия останова берут один из следующих:

— значение функции на данной итерации стало меньше заданого ε.

— изменение хk в результате итерации стало меньше заданого ε.

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод Ньютона онлайн

Данный онлайн калькулятор находит корень уравнения приближённо. В основе алгоритма его работы лежит метод Ньютона. Чтобы начать работу, необходимо ввести исходные данные своей задачи.

Методом Ньютона, найти корень (

максимальное кол-во итераций:

критерий останова вычислений:

Метод Ньютона является численным, т.е. корень уравнения находится приближенно. При этом можно заранее задать точность его нахождения.

Пусть нам дано уравнение

Формула для поиска корня уравнения выглядит следующим образом:

и — приближённые значения корня уравнения на -ой и ( )-ой итерациях соответственно, — значение функции в точке , — значение производной функции в точке .

Как видно, для того чтобы начать работу необходимо задать точку — начальное приближение для корня уравнения . От выбора точки зависит сойдётся ли алгоритм к решению или нет. Сходимость метода квадратичная, но она резко ухудшается если мы ищем кратный корень уравнения, т.е. если и одновременно , где — кратный корень уравнения .

Вычисления по приведённой выше формуле можно продолжать до бесконечности, соответственно на практике необходим некоторый критерий, который будет определять нужно ли нам продолжать вычисления или нет. Как правило, используется критерий останова вычислений на основе приращения или же на основе близости функции к нулю в некоторой точке .

Критерий останова вычислений на основе приращения задаётся следующей формулой:

т.е. различие (по модулю) между двумя последовательными приближениями к корню уравнения ( и ) должны быть меньше, некоторой наперёд заданной величины .

Критерий останова вычислений на основе близости функции к нулю определяется следующей формулой:

т.е. отличие (по модулю) между функцией в некоторой точке и нулём меньше .

В тоже время, если последовательность к корню не сходится, то критерии останова не сработают и процесс поиска корня будет продолжаться бесконечно. Чтобы предотвратить такую ситуацию, на практике вычисления прекращают после некоторого, заданного количества итераций.

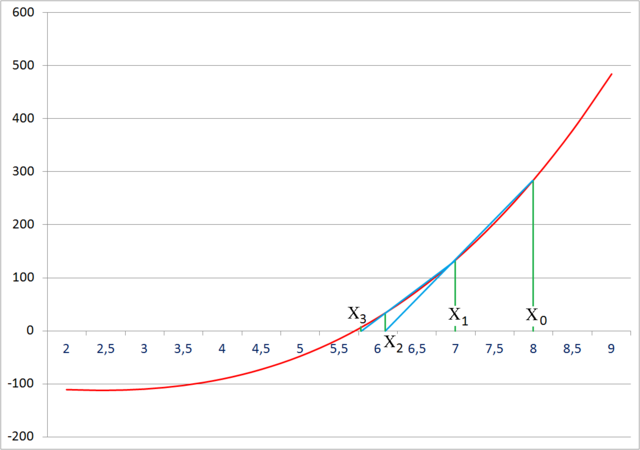
На рисунке ниже приведена геометрическая интерпретация процесса поиска корня уравнения методом Ньютона.

В точке мы строим касательную к графику функции . Уравнение касательной в этой точке имеет вид:

Находим точку пересечения полученной касательной с осью абсцисс, т.е. рассматриваем точку с координатами . Подставляя координаты указанной точки в уравнение касательной, получаем следующее соотношение:

Из данного уравнения находим :

Продолжая данный процесс, получим формулу метода Ньютона, приведенную выше. Из-за того, что на каждой итерации фактически происходит построение касательной, метод Ньютона также иногда называют методом касательных.

Видео:Метод секущихСкачать

Другие полезные разделы:

Видео:Численное решение уравнений, урок 3/5. Метод хордСкачать

Оставить свой комментарий:

Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме

Видео:Алгоритмы С#. Метод секущих(хорд)Скачать

Найти корень уравнения методом секущих онлайн

Нахождение знаменателя и первого члена целочисленной геометрической прогрессии по двум соседним членам.

Решение кубического уравнения по формуле Виета. Создан по запросу пользователя

Метод бисекции или метод деления отрезка пополам — простейший численный метод приближённого нахождения корня уравнения.

Метод секущих — итерационный численный метод приближённого нахождения корня уравнения.

Метод хорд — итерационный численный метод приближённого нахождения корня уравнения.

Калькулятор вычисляет обратный элемент по модулю

Решает квадратное уравнение, в том числе и с мнимыми корнями

Вычисление биссектрисы треугольника по длине трех сторон

Калькулятор вычисляет значения функции для заданных значений х

Строит график функции, заданной математической формулой.

Нахождение диагоналей параллелограмма по двум сторонам и углу между ними.

Вычисление длины стороны правильного многоугольника, если известна его площадь и число сторон

Вычисление длины стороны прямоугольного треугольника по двум другим с использованием теоремы Пифагора (создан по запросу пользователя)

Вычисление длины стороны треугольника по двум другим и углу между ними согласно теореме косинусов

Вычисление инволюты угла и нахождение угла по заданной инволюте

Вычисление площади поверхности и объема правильного, косого и усеченного конуса.

Формулы для круга

Вычисляет площадь сектора, длину дуги, периметр и центр масс кругового сектора

Вычисляет объем, площадь поверхности, радиус вписанной и описанной сферы.

Нахождение сторон треугольника по одной стороне и прилегающим углам. Создано по запросу пользователя

Нахождение углов треугольника по заданным сторонам с использованием теоремы косинусов

Вычисление обратных тригонометрических функций (арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс)

Рассчитывает объем геометрических фигур (куб, призма, пирамида, усеченная пирамида, конус, цилиндр, сфера, эллипсоид, тороид).

Расчет объема жидкости в цилиндрической таре, лежащей на боку (создано по запросу пользователя)

Вычисление объема цистерны по длине, диаметру и толщине стенок. Создано по запросу пользователя

Определение числа сторон и длины одной стороны правильного многоугольника, если задан радиус описанной и радиус вписанной окружности

Расчет площади многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники

Это простой калькулятор для вычисления площадьи трапеции. ВНИМАНИЕ. !Размеры вводить в САНТИМЕТРАХ!

Расчет площади четырехугольника по двум диагоналям и углу между ними. Описание процесса создания калькулятора

Подход к подсчету числа вложенных окружностей меньшего радиуса при известной длине описывающей окружности большего радиуса. Создано по запросу пользователя

Расчет параметров вписанной в правильный многоугольник и описанной вокруг него окружности

Калькулятор рассчитывает развертку (выкройку) на плоскости прямого кругового конуса и усеченного прямого кругового конуса

Калькулятор расcчитывает длину стропил, высоту и площадь кровли 4-х скатной крыши

Расчет площади прямоугольника при известном периметре и соотношении сторон

Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Два варианта расчета: 1) сегмент определен при помощи радиуса и угла 2) при помощи длины хорды и высоты

Вычисление площади поверхности и объема шарового сегмента или шарового слоя.

Построение синусоиды по параметрам пользователя

Расчет параметров вписанной в треугольник окружности

Расчет параметров описанной вокруг треугольника окружности

Онлайн калькулятор тригонометрических функций вычисляет синус ( sin ), косинус ( cos ), тангенс ( tg ), котангенс ( ctg ), секанс ( sec ), косеканс ( cosec ) для угла заданного в градусах, радианах, градах, минутах или секундах.

Калькуляторы рассчитвающие параметры по соотношениям между угловым размером тела, линейным размером тела и расстоянием до тела

Калькулятор рассчитывает глубину прогиба профиля трубогибом или гибочным станком для получения заданных параметров.

Вычисляет площадь поверхности и объем шарового сектора

Нахождение предела функции, по правилу Лопиталя, раскрывающий неопределённости вида 0/0 и ∞/∞.

Калькулятор вычисляет предел функции в заданной точке численным методом. Хорошо вычисляет предел функции, при х, приближающемуся к определенному значению. Не пригоден для вычисления пределов когда х, стремится к бесконечности.

Вычисляет производную заданной функции.