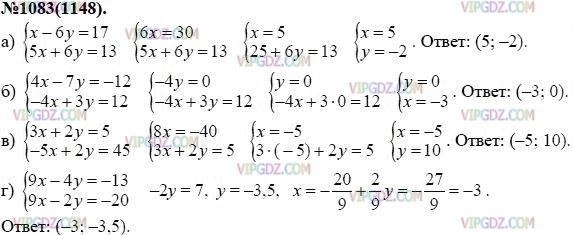Найдите решение системы уравнений x 6y 17 5x 6y 13 (6 видео)

Решение на Задание 1083 из ГДЗ по Алгебре за 7 класс: Макарычев Ю.Н.

Содержание

Условие
Решение 1
Решение 2
Популярные решебники
x-6*y=17 5*x+6*y=13
Решение
Решение задач по математике онлайн
Калькулятор онлайн. Решение системы двух линейных уравнений с двумя переменными. Метод подстановки и сложения.
Немного теории.
Решение систем линейных уравнений. Способ подстановки
Решение систем линейных уравнений способом сложения
Системы уравнений по-шагам
Результат
Примеры систем уравнений
Правила ввода
🎬 Видео

Условие

Решение 1

Решение 2

Поиск в решебнике

Видео:Решение систем уравнений методом подстановкиСкачать

x-6y=17 5x+6*y=13

Решение

Дана система ур-ний
$$x — 6 y = 17$$
$$5 x + 6 y = 13$$

Из 1-го ур-ния выразим y
$$x — 6 y = 17$$
Перенесем слагаемое с переменной x из левой части в правую со сменой знака
$$- 6 y = 17 — x$$
$$- 6 y = 17 — x$$
Разделим обе части ур-ния на множитель при y
$$frac = frac$$
$$y = frac — frac$$
Подставим найденное y в 2-е ур-ние
$$5 x + 6 y = 13$$
Получим:
$$5 x + 6 left(frac — fracright) = 13$$
$$6 x — 17 = 13$$
Перенесем свободное слагаемое -17 из левой части в правую со сменой знака
$$6 x = 13 + 17$$
$$6 x = 30$$
Разделим обе части ур-ния на множитель при x
$$frac = frac$$
$$x = 5$$
Т.к.
$$y = frac — frac$$
то
$$y = — frac + frac$$
$$y = -2$$

$$x — 6 y = 17$$
$$5 x + 6 y = 13$$

Приведём систему ур-ний к каноническому виду
$$x — 6 y = 17$$
$$5 x + 6 y = 13$$
Запишем систему линейных ур-ний в матричном виде
$$left[beginx_ — 6 x_\5 x_ + 6 x_endright] = left[begin17\13endright]$$
— это есть система уравнений, имеющая форму
A*x = B

Решение такого матричного ур-ния методом Крамера найдём так:

Т.к. определитель матрицы:
$$A = operatorname<left(left[begin1 & -6\5 & 6endright] right)> = 36$$
, то
Корень xi получается делением определителя матрицы Ai. на определитель матрицы A.
( Ai получаем заменой в матрице A i-го столбца на столбец B )
$$x_ = frac<operatorname<left(left[begin17 & -6\13 & 6endright] right)>> = 5$$
$$x_ = frac<operatorname<left(left[begin1 & 17\5 & 13endright] right)>> = -2$$

Дана система ур-ний
$$x — 6 y = 17$$
$$5 x + 6 y = 13$$

Приведём систему ур-ний к каноническому виду
$$x — 6 y = 17$$
$$5 x + 6 y = 13$$
Запишем систему линейных ур-ний в матричном виде
$$left[begin1 & -6 & 17\5 & 6 & 13endright]$$
В 1 ом столбце
$$left[begin1\5endright]$$
делаем так, чтобы все элементы, кроме
1 го элемента равнялись нулю.
— Для этого берём 1 ую строку
$$left[begin1 & -6 & 17endright]$$
,
и будем вычитать ее из других строк:
Из 2 ой строки вычитаем:
$$left[beginleft(-1right) 5 + 5 & 6 — — 30 & 13 — 5 cdot 17endright] = left[begin0 & 36 & -72endright]$$
получаем
$$left[begin1 & -6 & 17\0 & 36 & -72endright]$$
Во 2 ом столбце
$$left[begin-6\36endright]$$
делаем так, чтобы все элементы, кроме
2 го элемента равнялись нулю.
— Для этого берём 2 ую строку
$$left[begin0 & 36 & -72endright]$$
,
и будем вычитать ее из других строк:
Из 1 ой строки вычитаем:
$$left[begin1 — frac & -6 — frac & 17 — — -12endright] = left[begin1 & 0 & 5endright]$$
получаем
$$left[begin1 & 0 & 5\0 & 36 & -72endright]$$

Все почти готово — осталось только найти неизвестные, решая элементарные ур-ния:
$$x_ — 5 = 0$$
$$36 x_ + 72 = 0$$
Получаем ответ:
$$x_ = 5$$
$$x_ = -2$$

Видео:Система уравнений. Метод алгебраического сложенияСкачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Симметрические системы / Как решать по шаблону? x/y+y/x=13/6; x+y=5Скачать

Калькулятор онлайн.
Решение системы двух линейных уравнений с двумя переменными.
Метод подстановки и сложения.

С помощью данной математической программы вы можете решить систему двух линейных уравнений с двумя переменными методом подстановки и методом сложения.

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения двумя способами: методом подстановки и методом сложения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.

При вводе уравнений можно использовать скобки. При этом уравнения сначала упрощаются. Уравнения после упрощений должны быть линейными, т.е. вида ax+by+c=0 с точностью порядка следования элементов.
Например: 6x+1 = 5(x+y)+2

В уравнениях можно использовать не только целые, но также и дробные числа в виде десятичных и обыкновенных дробей.

Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например: 2.1n + 3,5m = 55

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &

Примеры.
-1&2/3y + 5/3x = 55
2.1p + 55 = -2/7(3,5p — 2&1/8q)

Решить систему уравнений

Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Немного теории.

Видео:Решение систем уравнений. Методом подстановки. Выразить YСкачать

Решение систем линейных уравнений. Способ подстановки

Последовательность действий при решении системы линейных уравнений способом подстановки:
1) выражают из какого-нибудь уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ left< begin 3x+y=7 \ -5x+2y=3 end right. $$

Выразим из первого уравнения y через x: y = 7-3x. Подставив во второе уравнение вместо y выражение 7-Зx, получим систему:
$$ left< begin y = 7—3x \ -5x+2(7-3x)=3 end right. $$

Нетрудно показать, что первая и вторая системы имеют одни и те же решения. Во второй системе второе уравнение содержит только одну переменную. Решим это уравнение:
$$ -5x+2(7-3x)=3 Rightarrow -5x+14-6x=3 Rightarrow -11x=-11 Rightarrow x=1 $$

Подставив в равенство y=7-3x вместо x число 1, найдем соответствующее значение y:
$$ y=7-3 cdot 1 Rightarrow y=4 $$

Пара (1;4) — решение системы

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы, не имеющие решений, также считают равносильными.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение систем линейных уравнений способом сложения

Рассмотрим еще один способ решения систем линейных уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Последовательность действий при решении системы линейных уравнений способом сложения:
1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ left< begin 2x+3y=-5 \ x-3y=38 end right. $$

В уравнениях этой системы коэффициенты при y являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной 3x=33. Заменим одно из уравнений системы, например первое, уравнением 3x=33. Получим систему
$$ left< begin 3x=33 \ x-3y=38 end right. $$

Из уравнения 3x=33 находим, что x=11. Подставив это значение x в уравнение ( x-3y=38 ) получим уравнение с переменной y: ( 11-3y=38 ). Решим это уравнение:
( -3y=27 Rightarrow y=-9 )

Таким образом мы нашли решение системмы уравнений способом сложения: ( x=11; y=-9 ) или ( (11; -9) )

Воспользовавшись тем, что в уравнениях системы коэффициенты при y являются противоположными числами, мы свели ее решение к решению равносильной системы (сумировав обе части каждого из уравнений исходной симтемы), в которой одно из уравнений содержит только одну переменную.

Видео:Решение системы уравнений методом ГауссаСкачать

Системы уравнений по-шагам

Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Результат

Примеры систем уравнений

Метод Гаусса
Метод Крамера
Прямой метод
Система нелинейных уравнений

Указанные выше примеры содержат также:

квадратные корни sqrt(x),
кубические корни cbrt(x)
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
показательные функции и экспоненты exp(x)
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
натуральные логарифмы ln(x),
десятичные логарифмы log(x)
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
обратные гиперболические функции:
asinh(x), acosh(x), atanh(x), actanh(x)
число Пи pi
комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте: