Видео:Квадратичная функция. Вершина параболы и нули функции. 8 класс.Скачать
Как найти вершину параболы: три формулы
Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.
Видео:Прямая y=7x-5 параллельна касательной к графику функции y=x^2+6x-8 Найдите абсциссу точки касания.Скачать
Нахождение вершины параболы: способы, примеры, советы
График функции y = ax 2 + bx + c, где a — первый коэффициент, b — второй коэффициент, c — свободный член, называется параболой. Но обратите внимание на тот факт, что a ≠0.
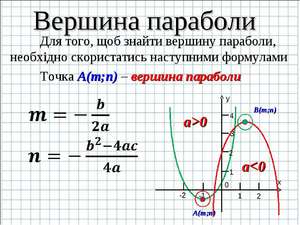
У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.
Первый способ
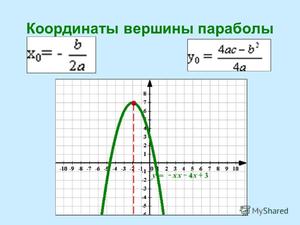
Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.
Например, y =x 2 –8 x +15;
находим первый, второй коэффициенты и свободный член;
подставляем значения a и b в формулу;
вычисляем значения y;
Значит, вершина находится в точке (4;-1).
Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n — корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.
Рассмотрим на примере y =x 2 –6x+5
1) Приравниваем к нулю:
2) Находим дискриминант, используя формулу: D = b 2 –4 ac:
3) Находим корни уравнения по формуле (-b±√ D)/2a:
- 1 — первый корень;
- 5 — второй корень.
Второй способ
Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.
1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x 2 + 8x = -10.
2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.
У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:
3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.
4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).
Третий способ
Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:
1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.
2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.
Рассмотрим этот способ подробнее.
Дана функция y = 4x²+16x-17;
- Записываем производную и приравниваем к нулю.
f'(x) = (4x²+16x-17)’ = 8x+16 =0
Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать
Построение параболы
Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.
Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2 +11 x -24 с вершиной в точке (5,5;-6,25).
1) Строим таблицу
| X | 5,5 |
| Y |
2) Заполняем таблицу
Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Видео:Задача 7 ЕГЭ по математике #2Скачать
Советы
Правильно находите коэффициенты.
Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.
Делайте всё поэтапно. Следуйте алгоритму.
Обратите ваше внимание на то, что:
- Нужно проверять правильно ли ваше решение.
- Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.
Видео:ЕГЭ задание 9 Точки перечечения параболСкачать
Видео
Это видео поможет вам научиться находить вершину параболы
Видео:Найти абсциссу второй точки пересечения параболы и прямойСкачать
Найдите абсциссу вершины параболы которая задается уравнением y 3×2 6x 5
Ответ:
а)координаты вершины параболы (0;6), нули функции: х₁=√6, х₂=-√6;
б) координаты вершины параболы (-10; 48), нули функции: х₁=-2, х₂=-8
Объяснение:
для вычисления координат вершины параболы можно воспользоваться формулами и :
чтобы найти нули функции, надо в уравнение графика подставить вместо у значение 0, иными словами, решить уравнение f(x)=0:
Видео:Парабола. Квадратичная функцияСкачать
Координаты вершины параболы онлайн
Парабола — это функция, заданная уравнением:
Её график имеет следующий вид:
Причем, в зависимости от знака коэффициента , ветви параболы направлены вверх (если ) или вниз (если ).
В школьном курсе алгебры возникает задача нахождения координат вершины параболы. Их можно найти по формулам:
Вершина параболы, отмечена оранжевой точкой на приведённом выше графике.
Наш онлайн калькулятор позволяет найти координаты вершины параболы с описанием подробного хода решения на русском языке. Для работы калькулятора, необходимо ввести уравнение параболы и указать её переменную. Уравнение параболы можно вводить в различных форматах, а коэффициентами могут быть не только числа или дроби, но и параметры. Нажмите на кнопку «Примеры», расположенную на панели калькулятора, чтобы посмотреть различные форматы ввода.
📽️ Видео
Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать
Прямая y=8x+11 параллельна касательной к графику функции y=x^2+7x-7. Найдите абсциссу точки касания.Скачать
10 задание. Все графики ЕГЭ по математике 2023Скачать
ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать
Прямая y=6х-5 касательная к графику функции y=3х^2+bх+7 Найдите b ( абсцисса точки касания больше 0)Скачать
Найдите вершину A параллелограмма ABCD, если B(3; −4; 7), C(−5; 3; −2) и D(1; 2; −3)Скачать
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
№ 40130 РешуЕгэ найти абсциссу точки, в которой касательная к графику функции параллельна прямойСкачать
Задание 11 (часть 1) | ЕГЭ 2024 Математика (профиль) | ГрафикиСкачать
Как найти абсциссу точки пересечения двух прямых?Скачать
Найти абсциссу точки пересечения графиков двух линейных функцийСкачать
Вершина параболы и ось симметрии. ПримерСкачать
Графики функций f(x)=5x+9 и g(x)=ax^2+bx+c пересекаются в точках A и B. Найдите абсциссу точки B.Скачать
