Напишите уравнения механической характеристики дпт нв и объясните физический смысл его слагаемых (6 видео)

Содержание

Уравнение механической характеристики ДПТ с НВ
Двигатель постоянного тока независимого возбуждения (ДПТ НВ)
Схема двигателя постоянного тока независимого возбуждения (ДПТ НВ)
Механическая характеристика двигателя постоянного тока независимого возбуждения (ДПТ НВ)
Механические характеристики двигателей постоянного тока
🎦 Видео

Видео:Электродвигатель постоянного тока. Принцип работы.Скачать

Уравнение механической характеристики ДПТ с НВ

С учетом третьего уравнения в системе (1.1) уравнение (1.2) можно переписать в виде зависимости со =ДМ), представляющей собой механическую характеристику ДПТ:

Данное уравнение определяет зависимость угловой скорости вращения от момента на валу двигателя. Поскольку в статике вращающий момент М равен моменту сопротивления М на валу ДПТ, то это уравнение определяет зависимость со от М.

Следует отметить, что величина электромагнитного момента М превышает выходной момент на валу на величину, соответствующую потерям в стали и механическим потерям от трения, но в большинстве практических расчетов указанными потерями можно пренебречь.

Коэффициент пропорциональности к • Ф можно считать постоянным для тех ДПТ с НВ, у которых имеются компенсационные обмотки, или в случае, когда можно пренебречь влиянием реакции якоря на величину Ф. В общем же случае влияние поперечной реакции якоря на величину магнитного потока Ф ведет к нарушению линейности механической характеристики по мере увеличения тока.

Видео:Урок 7. Механическое движение. Основные определения кинематики.Скачать

Двигатель постоянного тока независимого возбуждения (ДПТ НВ)

Двигатель постоянного тока независимого возбуждения (ДПТ НВ) В этом двигателе (рисунок 1) обмотка возбуждения подключена к отдельному источнику питания. В цепь обмотки возбуждения включен регулировочный реостат r_рег, а в цепь якоря — добавочный (пусковой) реостат R_п. Характерная особенность ДПТ НВ — его ток возбуждения I_в не зависит от тока якоря I_я так как питание обмотки возбуждения независимое.

Видео:Схема двигателя постоянного тока. Устройство и принцип работы.Скачать

Схема двигателя постоянного тока независимого возбуждения (ДПТ НВ)

Видео:Характиристики машин постоянного токаСкачать

Механическая характеристика двигателя постоянного тока независимого возбуждения (ДПТ НВ)

Уравнение механической характеристики двигателя постоянного тока независимого возбуждения имеет вид

где: n₀ — частота вращения вала двигателя при холостом ходе. Δn — изменение частоты вращения двигателя под действием механической нагрузки.

Из этого уравнения следует, что механические характеристики двигателя постоянного тока независимого возбуждения (ДПТ НВ) прямолинейны и пересекают ось ординат в точке холостого хода n₀ (рис 13.13 а), при этом изменение частоты вращения двигателя Δn, обусловленное изменением его механической нагрузки, пропорционально сопротивлению цепи якоря R_а =∑R + R_доб. Поэтому при наименьшем сопротивлении цепи якоря R_а = ∑R, когда R_доб = 0, соответствует наименьший перепад частоты вращения Δn. При этом механическая характеристика становится жесткой (график 1).

Механические характеристики двигателя, полученные при номинальных значениях напряжения на обмотках якоря и возбуждения и при отсутствии добавочных сопротивлений в цепи якоря, называют естественными рисунок 13.13, а (график 1 Rдоб = 0 ).

Если же хотя бы один из перечисленных параметров двигателя изменен (напряжение на обмотках якоря или возбуждения отличаются от номинальных значений, или же изменено сопротивление в цепи якоря введением R_доб), то механические характеристики называют искусственными .

Искусственные механические характеристики, полученные введением в цепь якоря добавочного сопротивления R_доб, называют также реостатными (графики 2 и 3).

При оценке регулировочных свойств двигателей постоянного тока наибольшее значение имеют механические характеристики n = f(M). При неизменном моменте нагрузки на валу двигателя с увеличением сопротивления резистора R_доб частота вращения уменьшается. Сопротивления резистора R_доб для получения искусственной механической характеристики, соответствующей требуемой частоте вращения n при заданной нагрузке (обычно номинальной) для двигателей независимого возбуждения:

где U — напряжение питания цепи якоря двигателя, В; I_я — ток якоря, соответствующий заданной нагрузке двигателя, А; n — требуемая частота вращения, об/мин; n₀ — частота вращения холостого хода, об/мин.

Частота вращения холостого хода n₀ представляет собой пограничную частоту вращения, при превышении которой двигатель переходит в генераторный режим. Эта частота вращения превышает номинальную n_ном на столько, на сколько номинальное напряжение U_ном подводимое к цепи якоря, превышает ЭДС якоря Е_{я ном} при номинальной нагрузки двигателя.

На форму механических характеристик двигателя влияет величина основного магнитного потока возбуждения Ф. При уменьшении Ф (при возрастании сопротивления резистора r_peг) увеличивается частота вращения холостого хода двигателя n₀ и перепад частоты вращения Δn. Это приводит к значительному изменению жесткости механической характеристики двигателя (рис. 13.13, б). Если же изменять напряжение на обмотке якоря U (при неизменных R_доб и R_рег), то меняется n₀, a Δn остается неизменным [см. (13.10)]. В итоге механические характеристики смещаются вдоль оси ординат, оставаясь параллельными друг другу (рис. 13.13, в). Это создает наиболее благоприятные условия при регулировании частоты вращения двигателей путем изменения напряжения U, подводимого к цепи якоря. Такой метод регулирования частоты вращения получил наибольшее распространение еще и благодаря разработке и широкому применению регулируемых тиристорных преобразователей напряжения.

Используемая литература: — Кацман М.М. Справочник по электрическим машинам

Видео:1) ТАУ (Теория автоматического управления) для чайников. Часть 1: основные понятия...Скачать

Механические характеристики двигателей постоянного тока

Аналитическое выражение механической характеристики двигателя постоянного тока можно получить из уравнения равновесия напряжений якорной цепи (при установившемся режиме)

Напишите уравнения механической характеристики дпт нв и объясните физический смысл его слагаемых

где U — напряжение на зажимах двигателя, В; 1_Я — ток в цепи якоря, A; R_я — сопротивление цепи якоря, Ом; Ф — магнитный поток двигателя, Вб; ω — угловая скорость якоря, рад/с; с_д — коэффициент, зависящий от конструктивных данных двигателя. Решив уравнение (3.1) относительно угловой скорости, получим уравнение скоростной характеристики двигателя

Электромагнитный вращающий момент двигателя (Н • м) пропорционален магнитному потоку и току якоря:

Из уравнения (3.3) ток якоря

Подставив в уравнение (3.2) значение тока, выраженное уравнением (3.4), получим уравнение механической характеристики двигателей постоянного тока независимо от способа возбуждения

Рассмотрим механические характеристики двигателей постоянного тока в зависимости от способа возбуждения.

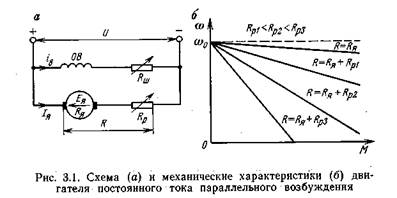
Двигатели постоянного тока параллельного возбуждения. Схема включения двигателя постоянного тока параллельного возбуждения приведена на рис. 3.1, а. Обмотка возбуждения ОВ может быть подключена к той же сети, что и якорь, или к отдельному источнику тока (независимое возбуждение). В том и другом случае ток возбуждения не зависит от процессов, происходящих в якоре двигателя и при постоянном напряжении сети магнитный поток можно считать постоянным Ф = const. Обозначив с_дФ=k_д и подставив его в уравнение (3.5), получим уравнение механической характеристики двигателя постоянного тока параллельного возбуждения

При М=0 угловая скорость якоря

называется скоростью идеального холостого хода.

Второй член уравнения (3.6) определяет изменение угловой скорости двигателя при изменении момента

Величина Δω зависит не только от момента, но и от сопротивления цепи якоря. С увеличением R_я величина Δω увеличивается. С учетом уравнений (3.7) и (3.8) уравнение (3.6) можно записать в виде

Из уравнений (3.6) и (3-.9) видно, что механическая характеристика двигателя параллельного возбуждения является прямой линией, тангенс угла наклона которой определяется величиной R_я/k_д 2

На рис. 3.1,6 приведены естественная и искусственные механические характеристики, полученные введением в цепь якоря реостата. Такие искусственные характеристики используются при пуске и торможении двигателя.

Двигатели постоянного тока последовательного возбуждения. Схема включения двигателя последовательного возбуждения приведена на рис. 3.2, а. Обмотка возбуждения ОВ включена последовательно с якорем и по ней протекает ток якоря. Следовательно, магнитный поток двигателя является функцией тока якоря. Эта зависимость выражается графически в виде кривой намагничивания, которая является нелинейной функцией и не имеет аналитического выражения. Поэтому нельзя получить аналитическую зависимость для механической характеристики.

Характерной особенностью двигателей последовательного возбуждения является то, что изменение магнитного потока с изменением тока якоря оказывает большое влияние на скорость двигателя. Это хорошо видно из уравнения скоростной характеристики

которое показывает, что с изменением магнитного потока скорость двигателя может изменяться в широких пределах.

Если для упрощения предположить, что магнитная цепь двигателя не насыщена и поток пропорционален току

то момент двигателя

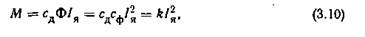Подставив в уравнение скоростной характеристики значение Ф = Сф/я, получим

где R — внутреннее сопротивление цепи якоря, равное сумме сопротивлений обмоток якоря и возбуждения (R_я + r_я).

Заменив в уравнении ток якоря его выражением из (3.10), получим уравнение механической характеристики

Уравнение (3.12) представляет собой уравнение кривой, для которой ось ординат является асимптотой. Подобная характеристика представлена на рис. 3.2,6. Уравнение (3.12) дает лишь общее представление о механической характеристике двигателя. При расчетах им пользоваться нельзя, так как аналитически учесть намагничивание стали невозможно. Как видно на рис. 3.2,6, механическая характеристика двигателя последовательного возбуждения — мягкая. При уменьшении нагрузки угловая скорость резко возрастает, а при М = 0 она стремится к бесконечности. В реальных двигателях ток при холостом ходе не может быть равен нулю вследствие потерь в стали и механических потерь, но угловая скорость может достигнуть опасных по условиям механической прочности значений, равных (5÷6)ω_ном. Поэтому холостой ход для двигателей последовательного возбуждения недопустим.

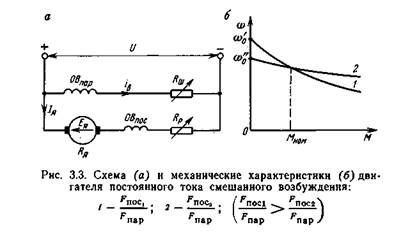
Двигатели постоянного тока смешанного возбуждения. Двигатели смешанного возбуждения имеют две обмотки возбуждения (рис. 3.3). Магнитный поток двигателя определяется суммой потоков параллельной ОВ_пар и последовательной ОВ_пос обмоток:

Вследствие нелинейной зависимости магнитного потока от тока якоря аналитическое выражение механической характеристики, так же как и для двигателя последовательного возбуждения, получить нельзя.

В зависимости от соотношения магнитных потоков обмоток возбуждения механические характеристики имеют различную жесткость. Чем больше доля магнитного потока последовательной обмотки, тем мягче характеристика. На рис. 3.3 приведены две естественные характеристики с различным соотношением магнитных потоков обмоток возбуждения. Обмотка параллельного возбуждения создает поток Ф_пар независимый от тока якоря, поэтому двигатель может работать вхолостую со скоростью