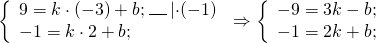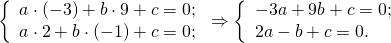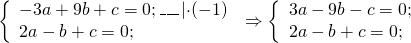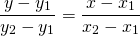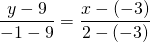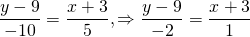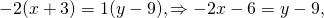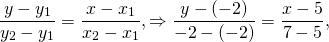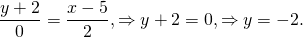Напишите уравнение прямой которая проходит через точку м 1 3 и середину отрезка ав

Геометрия | 5 — 9 классы

Напишите уравнение прямой, которая проходит через точку M(2 ; — 3) и середину отрезка AB, где A(4 ; 3) и B(6 ; — 9).

Координаты точки С — середины отрезка АВ :

Так как точки, через которые проходит прямая, имеют одинаковую ординату, то уравнение этой прямой

Видео:Составляем уравнение прямой по точкамСкачать

Прямая проходит через точки A (2 ; 1) и B(0 ; 3)?

Прямая проходит через точки A (2 ; 1) и B(0 ; 3).

Напишите уравнение прямой AB.

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Через середину C отрезок AB проведена прямая, перпендикулярная отрезку AB?

Через середину C отрезок AB проведена прямая, перпендикулярная отрезку AB.

Докажите , что каждая точка этой прямой удалена от точек A и B.

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Сделайте рисунок по описанию : а) прямая AB пересекает прямую MN в точке D ; б) прямая AB проходит через середину отрезка KL — точку O?

Сделайте рисунок по описанию : а) прямая AB пересекает прямую MN в точке D ; б) прямая AB проходит через середину отрезка KL — точку O.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Прямая а проходит через середину отрезка MN ?

Прямая а проходит через середину отрезка MN .

Докажите , что точки M и N находятся на одинаковом расстоянии от прямой а.

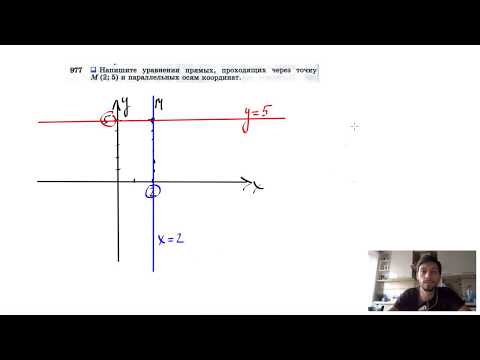
Видео:№977. Напишите уравнения прямых, проходящих через точку М (2; 5) и параллельных осям координат.Скачать

Составьте уравнение прямой которая проходит через середину ab и параллельна прямой y = 2x + 5 М(1 ; 3) — середина ab ОТДАЮ 90 баллов главное решите наконец ?

Составьте уравнение прямой которая проходит через середину ab и параллельна прямой y = 2x + 5 М(1 ; 3) — середина ab ОТДАЮ 90 баллов главное решите наконец !

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Через середину отрезка AB проведена прямая перпендикулярная прямой a b Докажите что каждая точка X этой прямой одинаково удалена от точки А и Б?

Через середину отрезка AB проведена прямая перпендикулярная прямой a b Докажите что каждая точка X этой прямой одинаково удалена от точки А и Б.

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Даны точки A( — 2 ; 0) и B(4 ; 6)?

Даны точки A( — 2 ; 0) и B(4 ; 6).

А)Запишите уравнение прямой AB.

Б)Составьте уравнение прямой, которая проходит через середину AB и параллельна прямой y = 2x + 5 / Напишите, пожалуста решение с пояснением!

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Отрезок AB = 16 см?

Отрезок AB = 16 см.

Точка M — середина отрезка AB, точка K — середина отрезка MB.

Найдите длину отрезка AK.

Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Даны точки A( — 2 ; 0) и B(4 ; 6) a) найдите расстояние между точками A и B б) запишите уравнение прямой AB в) составьте уравнение прямой, которая проходит через середину AB и параллельна прямой y = 2?

Даны точки A( — 2 ; 0) и B(4 ; 6) a) найдите расстояние между точками A и B б) запишите уравнение прямой AB в) составьте уравнение прямой, которая проходит через середину AB и параллельна прямой y = 2x + 5.

Видео:9 класс, 7 урок, Уравнение прямойСкачать

ОЧЕНЬ НУЖНО?

Даю 16б прямая n проходит через середину отрезка AB и перпендикулярна ему.

Докажите что каждая точка равноудаленная от точек A и B, лежит на прямой n.

На странице вопроса Напишите уравнение прямой, которая проходит через точку M(2 ; — 3) и середину отрезка AB, где A(4 ; 3) и B(6 ; — 9)? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

Нет условия задачи. Но если даны середины, то каждую середину нужно умножить на 2. Тогда можно будет узнать каждую сторону, и на основании этого построить треугольник.

(42 : 2) : 3 = 7 (ВС) 7×2 = 14 (АВ) Проверим : 14 : 2 = 7 получаем что АВ больше ВС в 2р Ищем S : S = АВ×ВС = 14×7 = 98 Рисунок не корректный. На нем АВ явно меньше ВС. А по условию наоборот, надо бы перерисовать)).

Видео:Уравнение окружности (1)Скачать

Интерактивный тест с автоматизированной проверкой ответа по теме «Прямая и окружность в координатах». Геометрия 9 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Описание презентации по отдельным слайдам:

Вариант 1 Вариант 2 Использован шаблон создания тестов в PowerPoint МКОУ «Погорельская СОШ» Кощеев М.М. Тест по теме: «Прямая и окружность в координатах»

Результат теста Верно: 14 Ошибки: 0 Отметка: 5 Время: 4 мин. 55 сек. ещё исправить

Вариант 1 в) 7 а) 3 б) -3 * 1. Найдите расстояние от начала координат до точки пересечения прямой 3х+7у+21=0 с осью абсцисс г) -7

Вариант 1 * б) б а) а в) д г) в, г д) а, б

Вариант 1 * 3. Дана точка М (6; -0,5). Среди прямых: а) 3х+4у-20=0 г) 3х-4у-20=0 б) 3х+4у+20=0 д) у=0,75х+6 в) 3х-4у+20=0 найдите все прямые, которые проходят через точку М. а) г б) б в) а, г г) г, д д) в

Вариант 1 * 4. Дана прямая 14х+13у-11=0. Среди точек М(-3;7), К(1;8), Р(-13;2), Е(0;7), Т(-13;0) найдите все такие точки, которые лежат с началом координат по одну сторону от данной прямой. д) Р, Т б) Р в) Е г) Е, Т а) М, К

Вариант 1 5. Напиши уравнение прямой , которая проходит через точку М(-1;3) и середину отрезка АВ, где А(2;17) и В(-11;-11). * в) у=3 б) у-х=4 д) 5х+3у-4=0 г) х=-1 а) х+у=2

Вариант 1 * г) 13у+5х=0 б) 13х-5у=0 в) 13у-5х=0 д) Такой прямой не существует а) 13х+5у=0

Вариант 1 * 7. Рассматриваются треугольники АВС, у которых вершина А(0;7)- общая , а вершины В и С расположены на прямой у=2х. Тогда средние линии всех таких треугольников лежат на прямой , уравнение которой имеет вид: б) 4х-2у+7=0 г) 4х-2у+3,5=0 в) 2х-4у+3,5=0 д) 2х+4у+14=0 а) 4х+2у+7=0

Вариант 1 * 8. Прямые у=3х-1, у=3х+5 и у=3х+7 пересекают прямую 47х+74у-11=0 соответственно в точках А, В и С. Найдите отношение длин отрезков АВ и ВС. а) 3:1 б) 7:5 в) 47:74 г) 2:1 д) невозможно определить

Вариант 1 * 9. Найти длину отрезка прямой 4х+3у=12, все точки которого имеют неотрицательные и абсциссы и ординаты. д) 5 б) 2 г) 4 а) 1

Вариант 1 * б) 15° д) 105° в) 30° г) 45° а) 10°

Вариант 1 11. Какие из перечисленных ниже прямых содержат биссектрису одного из углов, образованных прямыми у=5х-3 и у=-5х+17? * б) х=2 г) у=х+7 в) у=3 д) у=-3 а) х=0

Вариант 1 12. Окружность с центром (1;-2) и радиусом 3 задается уравнением: * д) (х-1)²+(у+2)²=9 г) (х+2)²+(у-1)²=9 в) (х-1)²+(у+2)²=3 б) (х-1)²+(у-2)²=9 а) (х+1)²+(у-2)²=9

Вариант 1 * 13. Множество всех точек, координаты которых удовлетворяют уравнению х²+3х=11-у², являются: б) окружностью г) гиперболой в) прямой д) параболой а) одной точкой

Вариант 1 * 14. Даны точки А(-1;1) и В(3;-3). Уравнение окружности с диаметром АВ имеет вид: а) (х-1)²+(у+1)²=8 г) (х+1)²+(у-1)²=8 в) (х-1)²+(у+1)²=32 б) (х-1)²+(у+1)²=2 д) (х-4)²+(у+4)²=16

Вариант 2 а) 3 в) 7 б) -3 * 1. Найдите расстояние от начала координат до точки пересечения прямой 3х+7у-21=0 с осью ординат. г) -7

Вариант 2 * а) а б) б в) д г) в, г д) а, б

Вариант 2 * 3. Дана точка М (7; -0,25). Среди прямых: а) 3х+4у-20=0 г) 3х-4у-20=0 б) 3х+4у+20=0 д) у=0,75х+6 в) 3х-4у+20=0 найдите все прямые, которые проходят через точку М. в) а б) б, г а) г г) г, д д) в

Вариант 2 * 4. Дана прямая 14х+12у-9=0. Среди точек М(3;7), К(1;8), Р(-13;2), Е(0;7), Т(0;-13) найдите все такие точки, которые лежат с началом координат по одну сторону от данной прямой. г) Р, Т б) Р в) Е д) Е, Т а) М, К

Вариант 2 5. Напиши уравнение прямой , которая проходит через точку М(-2;3) и середину отрезка АВ, где А(4; 3) и В(-8; 9). * г) х=-2 б) у-х=4 д) 5х+3у-4=0 в) у=3 а) х+у=2

Вариант 2 * б) 13х-4у=0 г) 13у+4х=0 в) 13у-4х=0 д) Такой прямой не существует а) 13х+4у=0

Вариант 2 * 7. Рассматриваются треугольники АВС, у которых вершина А(0;-8)- общая , а вершины В и С расположены на прямой у=3х. Тогда средние линии всех таких треугольников лежат на прямой , уравнение которой имеет вид: д) 3х-у-4=0 г) 3х+4у+14=0 в) 3х-4у+4=0 б) 4х-у+4=0 а) 3х+у+4=0

Вариант 2 * 8. Прямые у=-3х+1, у=-3х-5 и у=-3х-7 пересекают прямую 27х+72у-11=0 соответственно в точках С, В и А. Найдите отношение длин отрезков АС и ВС. г) 4:3 б) 7:2 в) 27:72 а) 3:4 д) невозможно определить

Вариант 2 * 9. Найти длину отрезка прямой 12х-5у+60=0, все точки которого имеют неположительные абсциссы и неотрицательные ординаты. б) 13 д) 5 г) 14 а) 11

Вариант 2 * д) 15° б) 105° в) 30° г) 45° а) 10°

Вариант 2 11. Какие из перечисленных ниже прямых содержат биссектрису одного из углов, образованных прямыми у=3х-5 и у=-3х+19? * в) у=7 г) у=х+7 б) х=2 д) у=-3 а) х=0

Вариант 2 12. Окружность с центром (-2; 1) и радиусом 3 задается уравнением: * г) (х+2)²+(у-1)²=9 д) (х-1)²+(у+2)²=9 в) (х-1)²+(у+2)²=3 б) (х-1)²+(у-2)²=9 а) (х+1)²+(у-2)²=9

Вариант 2 * 13. Множество всех точек, координаты которых удовлетворяют уравнению х²+9=6у-у², являются: д) одной точкой г) гиперболой в) прямой б) окружностью а) параболой

Вариант 2 * 14. Даны точки А(-1;-1) и В(3;3). Уравнение окружности с диаметром АВ имеет вид: б) (х-1)²+(у-1)²=8 г) (х+1)²+(у-1)²=8 в) (х-1)²+(у+1)²=32 а) (х-1)²+(у+1)²=8 д) (х-4)²+(у+4)²=16

Ключи к тесту: «Прямая и окружность в координатах». * Литература Л.И. Звавич, Е,В. Потоскуев Тесты по геометрии 9 класс к учебнику Л.С. Атанасяна и др. М. : издательство «Экзамен» 2013г.- 128с. 1 вариант1234567891011121314 Отв.вбадвгбадббдба 2 вариант1234567891011121314 Отв.аавггбдгбдвгдб

Краткое описание документа:

Вариант 1 Вариант 2 Использован шаблон создания тестов в PowerPoint МКОУ «Погорельская СОШ» Кощеев М.М. Тест по теме: «Прямая и окружность в координатах» Результат теста Верно: 14 Ошибки: 0 Отметка: 5 Время: 4 мин. 55 сек. ещё исправить Вариант 1 в) 7 а) 3 б) -3 * 1. Найдите расстояние от начала координат до точки пересечения прямой 3х+7у+21=0 с осью абсцисс г) -7 Вариант 1 * б) б а) а в) д г) в, г д) а, б Вариант 1 * 3. Дана точка М (6; -0,5). Среди прямых: а) 3х+4у-20=0 г) 3х-4у-20=0 б) 3х+4у+20=0 д) у=0,75х+6 в) 3х-4у+20=0 найдите все прямые, которые проходят через точку М. а) г б) б в) а, г г) г, д д) в Вариант 1 * 4. Дана прямая 14х+13у-11=0. Среди точек М(-3;7), К(1;8), Р(-13;2), Е(0;7), Т(-13;0) найдите все такие точки, которые лежат с началом координат по одну сторону от данной прямой. д) Р, Т б) Р в) Е г) Е, Т а) М, К Вариант 1 5. Напиши уравнение прямой , которая проходит через точку М(-1;3) и середину отрезка АВ, где А(2;17) и В(-11;-11). * в) у=3 б) у-х=4 д) 5х+3у-4=0 г) х=-1 а) х+у=2 Вариант 1 * г) 13у+5х=0 б) 13х-5у=0 в) 13у-5х=0 д) Такой прямой не существует а) 13х+5у=0 Вариант 1 * 7. Рассматриваются треугольники АВС, у которых вершина А(0;7)- общая , а вершины В и С расположены на прямой у=2х. Тогда средние линии всех таких треугольников лежат на прямой , уравнение которой имеет вид: б) 4х-2у+7=0 г) 4х-2у+3,5=0 в) 2х-4у+3,5=0 д) 2х+4у+14=0 а) 4х+2у+7=0 Вариант 1 * 8. Прямые у=3х-1, у=3х+5 и у=3х+7 пересекают прямую 47х+74у-11=0 соответственно в точках А, В и С. Найдите отношение длин отрезков АВ и ВС. а) 3:1 б) 7:5 в) 47:74 г) 2:1 д) невозможно определить Вариант 1 * 9. Найти длину отрезка прямой 4х+3у=12, все точки которого имеют неотрицательные и абсциссы и ординаты. д) 5 б) 2 г) 4 а) 1 Вариант 1 * б) 15° д) 105° в) 30° г) 45° а) 10° Вариант 1 11. Какие из перечисленных ниже прямых содержат биссектрису одного из углов, образованных прямыми у=5х-3 и у=-5х+17? * б) х=2 г) у=х+7 в) у=3 д) у=-3 а) х=0 Вариант 1 12. Окружность с центром (1;-2) и радиусом 3 задается уравнением: * д) (х-1)²+(у+2)²=9 г) (х+2)²+(у-1)²=9 в) (х-1)²+(у+2)²=3 б) (х-1)²+(у-2)²=9 а) (х+1)²+(у-2)²=9 Вариант 1 * 13. Множество всех точек, координаты которых удовлетворяют уравнению х²+3х=11-у², являются: б) окружностью г) гиперболой в) прямой д) параболой а) одной точкой Вариант 1 * 14. Даны точки А(-1;1) и В(3;-3). Уравнение окружности с диаметром АВ имеет вид: а) (х-1)²+(у+1)²=8 г) (х+1)²+(у-1)²=8 в) (х-1)²+(у+1)²=32 б) (х-1)²+(у+1)²=2 д) (х-4)²+(у+4)²=16 Вариант 2 а) 3 в) 7 б) -3 * 1. Найдите расстояние от начала координат до точки пересечения прямой 3х+7у-21=0 с осью ординат. г) -7 Вариант 2 * а) а б) б в) д г) в, г д) а, б Вариант 2 * 3. Дана точка М (7; -0,25). Среди прямых: а) 3х+4у-20=0 г) 3х-4у-20=0 б) 3х+4у+20=0 д) у=0,75х+6 в) 3х-4у+20=0 найдите все прямые, которые проходят через точку М. в) а б) б, г а) г г) г, д д) в Вариант 2 * 4. Дана прямая 14х+12у-9=0. Среди точек М(3;7), К(1;8), Р(-13;2), Е(0;7), Т(0;-13) найдите все такие точки, которые лежат с началом координат по одну сторону от данной прямой. г) Р, Т б) Р в) Е д) Е, Т а) М, К Вариант 2 5. Напиши уравнение прямой , которая проходит через точку М(-2;3) и середину отрезка АВ, где А(4; 3) и В(-8; 9). * г) х=-2 б) у-х=4 д) 5х+3у-4=0 в) у=3 а) х+у=2 Вариант 2 * б) 13х-4у=0 г) 13у+4х=0 в) 13у-4х=0 д) Такой прямой не существует а) 13х+4у=0 Вариант 2 * 7. Рассматриваются треугольники АВС, у которых вершина А(0;-8)- общая , а вершины В и С расположены на прямой у=3х. Тогда средние линии всех таких треугольников лежат на прямой , уравнение которой имеет вид: д) 3х-у-4=0 г) 3х+4у+14=0 в) 3х-4у+4=0 б) 4х-у+4=0 а) 3х+у+4=0 Вариант 2 * 8. Прямые у=-3х+1, у=-3х-5 и у=-3х-7 пересекают прямую 27х+72у-11=0 соответственно в точках С, В и А. Найдите отношение длин отрезков АС и ВС. г) 4:3 б) 7:2 в) 27:72 а) 3:4 д) невозможно определить Вариант 2 * 9. Найти длину отрезка прямой 12х-5у+60=0, все точки которого имеют неположительные абсциссы и неотрицательные ординаты. б) 13 д) 5 г) 14 а) 11 Вариант 2 * д) 15° б) 105° в) 30° г) 45° а) 10° Вариант 2 11. Какие из перечисленных ниже прямых содержат биссектрису одного из углов, образованных прямыми у=3х-5 и у=-3х+19? * в) у=7 г) у=х+7 б) х=2 д) у=-3 а) х=0 Вариант 2 12. Окружность с центром (-2; 1) и радиусом 3 задается уравнением: * г) (х+2)²+(у-1)²=9 д) (х-1)²+(у+2)²=9 в) (х-1)²+(у+2)²=3 б) (х-1)²+(у-2)²=9 а) (х+1)²+(у-2)²=9 Вариант 2 * 13. Множество всех точек, координаты которых удовлетворяют уравнению х²+9=6у-у², являются: д) одной точкой г) гиперболой в) прямой б) окружностью а) параболой Вариант 2 * 14. Даны точки А(-1;-1) и В(3;3). Уравнение окружности с диаметром АВ имеет вид: б) (х-1)²+(у-1)²=8 г) (х+1)²+(у-1)²=8 в) (х-1)²+(у+1)²=32 а) (х-1)²+(у+1)²=8 д) (х-4)²+(у+4)²=16 Ключи к тесту: «Прямая и окружность в координатах». * Литература Л.И. Звавич, Е,В. Потоскуев Тесты по геометрии 9 класс к учебнику Л.С. Атанасяна и др. М. : издательство «Экзамен» 2013г.- 128с. 1 вариант 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Отв. в б а д в г б а д б б д б а 2 вариант 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Отв. а а в г г б д г б д в г д б

Видео:Уравнение прямой, проходящей через две точкиСкачать

Составить уравнение прямой, проходящей через две точки

Рассмотрим, как составить уравнение прямой, проходящей через две точки, на примерах.

Составить уравнение прямой, проходящей через точки A(-3; 9) и B(2;-1).

1 способ — составим уравнение прямой с угловым коэффициентом.

Уравнение прямой с угловым коэффициентом имеет вид y=kx+b. Подставив координаты точек A и B в уравнение прямой (x= -3 и y=9 — в первом случае, x=2 и y= -1 — во втором), получаем систему уравнений, из которой находим значения k и b:

Сложив почленно 1-е и 2-е уравнения, получим: -10=5k, откуда k= -2. Подставив во второе уравнение k= -2, найдём b: -1=2·(-2)+b, b=3.

Таким образом, y= -2x+3 — искомое уравнение.

2 способ — составим общее уравнение прямой.

Общее уравнение прямой имеет вид ax+by+c=0. Подставив координаты точек A и B в уравнение, получаем систему:

Поскольку количество неизвестных больше количества уравнений, система не разрешима. Но можно все переменные выразить через одну. Например, через b.

Умножив первое уравнение системы на -1 и сложив почленно со вторым:

получим: 5a-10b=0. Отсюда a=2b.

Подставим полученное выражение во второе уравнение: 2·2b -b+c=0; 3b+c=0; c= -3b.
Подставляем a=2b, c= -3b в уравнение ax+by+c=0:

2bx+by-3b=0. Осталось разделить обе части на b:

Общее уравнение прямой легко приводится к уравнению прямой с угловым коэффициентом:

3 способ — составим уравнение прямой, проходящей через 2 точки.

Уравнение прямой, проходящей через две точки, имеет вид:

Подставим в это уравнение координаты точек A(-3; 9) и B(2;-1)

В школьном курсе чаще всего используется уравнение прямой с угловым коэффициентом. Но самый простой способ — вывести и использовать формулу уравнения прямой, проходящей через две точки.

Если при подстановке координат заданных точек один из знаменателей уравнения

окажется равным нулю, то искомое уравнение получается приравниваем к нулю соответствующего числителя.

Составить уравнение прямой, проходящей через две точки C(5; -2) и D(7;-2).

Подставляем в уравнение прямой, проходящей через 2 точки, координаты точек C и D:

Составить уравнение прямой, проходящей через точки M (7; 3) и N (7; 11).

💡 Видео

№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать

№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

12. Уравнения прямой в пространстве Решение задачСкачать

Уравнение параллельной прямойСкачать

Уравнение прямой, проходящей через точку параллельно OX, OY или через начало координат. Урок 5. 8 клСкачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Координаты середины отрезкаСкачать

Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать