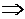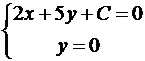Написать уравнение прямой проходящей через точку параллельно вектору (8 видео)

Уравнения прямой в пространстве векторное, общее, канонические, параметрические (Таблица)

Способ задания прямой в пространстве

Вид уравнения прямой

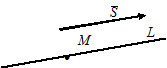
Векторное уравнение прямой, проходящей через точку М параллельно заданному вектору s .

s — направляющий вектор прямой

где t — скалярный множитель (параметр)

Канонические уравнения прямой, проходящей через точку M₀(x₀,y₀,z₀) и параллельно вектору s =

Написать уравнение прямой проходящей через точку параллельно вектору

Параметрические уравнения прямой, проходящей через точку (x₀,y₀,z₀) параллельно вектору s = <m,n,p]

Прямая как линия пересечения двух непараллельных плоскостей (общие уравнения прямой)

Содержание

Математический портал
Nav view search
Navigation
Search
Прямая в пространстве, всевозможные уравнения.
Уравнение параллельной прямой
📹 Видео

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Математический портал

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Nav view search

Search

Вы здесь:
Home
Аналитическая геометрия
Прямая в пространстве.

Видео:12. Уравнения прямой в пространстве Решение задачСкачать

Прямая в пространстве, всевозможные уравнения.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Существуют такие формы записи уравнения прямой в пространстве:

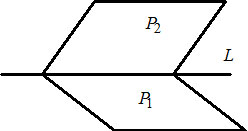
1) $left<beginA_1x+B_1y+C_1z+D_1=0quad (P_1)\ A_2x+B_2y+C_2z+D_2=0quad (P_2)endright. — $ общее уравнение прямой $L$ в пространстве, как линии пересечения двух плоскостей $P_1$ и $P_2.$

2) $frac=frac=frac

-$ каноническое уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0, z_0)$ параллельно вектору $overline~~=(m, n, p).$ Вектор $overline S$ является направляющим вектором прямой $L.$~~

~~3) $frac=frac=frac -$ уравнение прямой, которая проходит через две точки $A(x_1, y_1, z_1)$ и $B(x_2, y_2, z_2).$~~

4) Приравнивая каждую из частей канонического уравнения 2 к прараметру $t,$ получаем параметрическое уравнение прямой:

~~Расположение двух прямых в пространстве.~~

Условие параллельности двух прямых: Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $overline~~_1paralleloverline~~_2Leftrightarrow$ $frac=frac=frac~~~~

Условие перпендикулярности двух прямых: $L_1perp L_2Leftrightarrow$ $overline~~_1perpoverline~~_2Leftrightarrow$ $cdot+cdot+p_1cdot p_2=0.$~~~~

~~Угол между прямыми:~~

Расстояние от точки до прямой равно длине перпендикуляра, опущенного из точки на данную прямую.

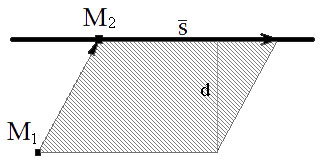
~~Пусть прямая $L$ задана уравнением $frac=frac=frac~~

,$ следовательно $overline S=(m, n, p).$ Пусть также $M_2=(x_2, y_2, z_2) -$ произвольная точка, принадлежащая прямой $L.$ Тогда расстояние от точки $M_1=(x_1, y_1, z_1)$ до прямой $L$ можно найти по формуле: $$d(M_1, L)=frac<|[overline, overline S]|>.$$

~~Примеры.~~

2.198. Написать каноническое уравнение прямой, проходящей через точку $M_0(2, 0, -3)$ параллельно:

~~а) вектору $q(2, -3, 5);$~~

~~е) прямой $x=-2+t, y=2t, z=1-fract.$~~

~~Решение.~~

~~а) Воспользуемся формулой (2) уравнения прямой в пространстве:~~

~~$frac=frac=frac~~

-$ каноническое уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0, z_0)$ параллельно вектору $overline~~=(m, n, p).$~~

~~По условию $M_0(2, 0, -3)$ и $overline~~=q(2,-3,5).$~~~~

б) Прямая, параллельная заданной прямой, должна быть параллельна ее направляющему вектору. Направляющий вектор прямой $frac=frac=frac$ имеет координаты $overline S(5, 2, -1).$ Далее, находим уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(5, 2, -1)$ как и в пункте а):

в) ось OX имеет направляющий вектор $i=(1, 0, 0).$ Таким образом, ищем уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $i(1, 0, 0):$

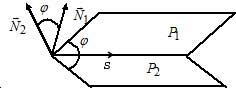
д) Прямая, заданная как пересечение двух плоскостей перпендикулярна нормалям обеих плоскостей , поэтому Направляющий вектор прямой

~~$left<begin3x-y+2z-7=0,\ x+3y-2z-3=0; endright.$ можно найти как векторное произведение нормалей заданных плоскостей.~~

~~Для плоскости $P_1:$ $3x-y+2z-7=0$ нормальный вектор имеет координаты $N_1(3, -1, 2);$~~

~~для плосости $P_2:$ $x+3y-2z-3,$ нормальный вектор имеет координаты $N_2(1, 3, -2).$~~

~~Находим векторное произведение:~~

~~Таким образом, направляющий вектор прямой $left<begin3x-y+2z-7=0,\ x+3y-2z-3=0; endright.$ имеет координаты $overline S (-4, 8, 10).$~~

~~Далее нам необходимо найти уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(-4, 8, 10):$~~

е) Найдем направляющий вектор прямой $x=-2+t, y=2t, z=1-fract.$ Для этого запишем уравнение этой прямой в каноническом виде:

Отсюда находим направляющий вектор $overline Sleft(1, 2, -fracright).$ Умножим координаты направляющего вектора на 2 (чтобы избавиться от дроби): $overline S_1(2, 4, -1).$

~~Далее нам необходимо найти уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(2, 4, -1):$~~

2.199(a). Написать уравнение прямой, проходящей через две заданные точки $M_1 (1, -2, 1)$ и $M_2(3, 1, -1).$

~~Решение.~~

~~Воспользуемся формулой (3) уравнения прямой в пространстве:~~

~~$frac=frac=frac -$ уравнение прямой, которая проходит через две точки $A(x_1, y_1, z_1)$ и $B(x_2, y_2, z_2).$~~

~~Подставляем заданные точки:~~

2.204. Найти расстояние между параллельными прямыми

~~Решение.~~

Расстояние между параллельными прямыми $L_1$ и $L_2$ равно расстоянию от произвольной точки прямой $L_1$ до прямой $L_2.$ Следовательно, его можно найти по формуле $$d(L_1, L_2)=d(M_1, L_2)=frac<|[overline, overline S]|>,$$ где $M_1-$ произвольная точка прямой $L_1,$ $M_2 — $произвольная точка прямой $L_2,$ $overline S -$ направляющий вектор прямой $L_2.$

~~Из канонических уравнений прямых берем точки $M_1=(2, -1, 0)in L_1,$ $M_2=(7, 1, 3)in L_2,$ $overline S=(3, 4, 2). $~~

~~Отсюда находим $overline=(7-2, 1-(-1),3-0)=(5, 2, 3);$~~

Ответ: 3.

~~2.205 (а). Найти расстояние от точки $A(2, 3, -1)$ до заданной прямой $L:$ $left<begin2x-2y+z+3=0,\ 3x-2y+2z+17=0 endright.$~~

~~Решение.~~

Для того, чтобы найти расстояние от точки $A$ до прямой $L,$ нам необходимо выбрать произвольную точку $M,$ принадлежащую прямой $L$ и найти направляющий вектор этой прямой.

~~Выбираем точку $M.$ Пусть координата $z=0.$ Подставим это значение в данную систему:~~

~~Таким образом, $M=(-14, -frac, 0)$~~

~~Направляющий вектор найдем, как векторное произведение нормалей заданных плоскостей:~~

~~Для плоскости $P_1:$ $2x-2y+z+3=0$ нормальный вектор имеет координаты $N_1(2, -2, 1);$~~

~~для плосости $P_2:$ $3x+2y+2z+17=0,$ нормальный вектор имеет координаты $N_2(3, -2, 2).$~~

~~Находим векторное произведение:~~

~~Таким образом, направляющий вектор прямой $left<begin2x-2y+z+3=0,\ 3x-2y+2z+17=0 endright.$~~

~~имеет координаты $overline S (-2, -1, 2).$~~

~~Теперь можно воспользоваться формулой $$d(A, L)=frac<|[overline, overline S]|>.$$~~

~~$overline=left(2-(-14),3-left(-fracright),-1-0right)=left(16, 15frac, -1right)$~~

Ответ: $d(A, L)=15.$

2.212. Написать каноническое уравнение прямой, которая проходит через точку $M_0(3, -2, -4)$ параллельно плоскости $P: 3x-2y-3z-7=0$ и пересекает прямую $L: frac=frac=frac.$

~~Решение.~~

~~Запишем уравнение плоскости $P_1,$ которая проходит через точку $M_0(3, -2, -4)$ параллельно плоскости $3x-2y-3z-7=0:$~~

$P: 3x-2y-3z-7=0Rightarrow overline N=(3; -2; -3).$ Искомая плоскость проходит через точку $M_0(3, -2, -4)$ перпендикулярно вектору $overline N(3, -2, -3).$

~~$P_1: 3x-9-2y-4-3z-12=0 Rightarrow$~~

Далее найдем точку пересечения плоскости $P_1$ и прямой $L.$ Для этого запишем уравнение прямой $L$ в параметрической форме:

Далее, подставим значения $x, y$ и $z,$ выраженные через $t$ в уравнение плоскости $P_1,$ и из полученного уравнения выразм $t:$

~~Подставляя найденное занчение $t$ в уравнение прямой $L,$ найдем координаты точки пересечения:~~

~~Таким образом, прямая $L$ и плоскость $P_1$ пересекаются в точке $M_1(8, -8, 5).$~~

Теперь запишем уравнение прямой, проходящей через точки $M_0(3, -2. -4)$ и $M_1(8, -8, 5)$— это и будет искомая прямая. Воспользуемся формулой ( 3) $frac=frac=frac :$

~~2.199.~~

~~б) Написать уравнение прямой, проходящей через две заданные точки $M_1 (3, -1, 0)$ и $M_2(1, 0, -3).$~~

~~б) Найти расстояние от точки $A(2, 3, -1)$ до заданной прямой $ L:$ $left<beginx=3t+5,\ y=2t,\z=-2t-25. endright.$~~

2.206. Доказать, что прямые $L_1: left<begin2x+2y-z-10=0,\ x-y-z-22=0, endright.$ и $L_2: frac=frac=frac.$ параллельны и найти расстояние $rho(L_1, L_2)$

2.207. Составить уравнения прямой, проходящей через точки пересечения плоскости $x-3y+2z+1=0$ с прямыми $frac=frac=frac$ и $frac=frac=frac.$

2.211. Написать уравнение прямой, проходящей через точку $M_0(7, 1, 0)$ параллельно плоскости $2x+3y-z-15=0$ и пересекающей прямую $frac=frac=frac.$

~~Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать~~

Уравнение параллельной прямой

Альтернативная формула:
Прямая, проходящая через точку M₁(x₁; y₁) и параллельная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения параллельной прямой (см. также как составить уравнение перпендикулярной прямой).

Пример №2 . Написать уравнение прямой, параллельной прямой 2x + 5y = 0 и образующей вместе с осями координат треугольник, площадь которого равна 5.
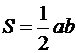
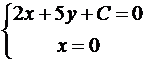
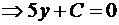
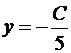
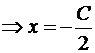
Решение. Так как прямые параллельны, то уравнение искомой прямой 2x + 5y + C = 0. Площадь прямоугольного треугольника , где a и b его катеты. Найдем точки пересечения искомой прямой с осями координат:
;
.
Итак, A(-C/2,0), B(0,-C/5). Подставим в формулу для площади: 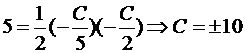. Получаем два решения: 2x + 5y + 10 = 0 и 2x + 5y – 10 = 0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-2; 5) и параллельной прямой 5x-7y-4=0 .
Решение. Данную прямую можно представить уравнением y = 5 /₇x – 4 /₇ (здесь a = 5 /₇). Уравнение искомой прямой есть y – 5 = 5 / 7(x – (-2)), т.е. 7(y-5)=5(x+2) или 5x-7y+45=0 .

~~Пример №4 . Решив пример 3 (A=5, B=-7) по формуле (2), найдем 5(x+2)-7(y-5)=0.~~

Пример №5 . Составить уравнение прямой, проходящей через точку (-2;5) и параллельной прямой 7x+10=0.
Решение. Здесь A=7, B=0. Формула (2) дает 7(x+2)=0, т.е. x+2=0. Формула (1) неприменима, так как данное уравнение нельзя разрешить относительно y (данная прямая параллельна оси ординат).