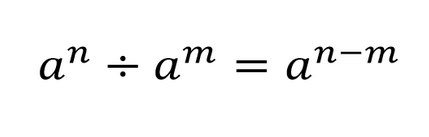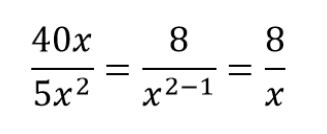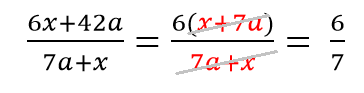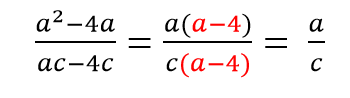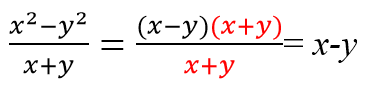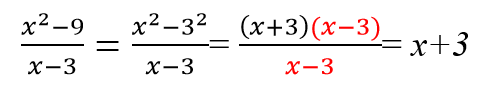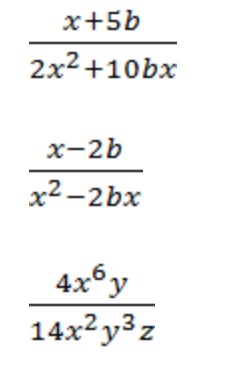Для начала вспомним основные формулы степеней и их свойства.
Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a•a•…•a=a n
3. a n • a m = a n + m
5. a n b n = (ab) n
7. a n /a m = a n — m
Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.
Примеры показательных уравнений:
В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.
Приведем еще примеры показательных уравнений.
2 x *5=10
16 x — 4 x — 6=0
Теперь разберем как решаются показательные уравнения?
Возьмем простое уравнение:
Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:
Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.
Теперь подведем итоги нашего решения.
Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.
Теперь прорешаем несколько примеров:
Начнем с простого.
Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.
x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2
В следующем примере видно, что основания разные это 3 и 9.
Для начала переносим девятку в правую сторону, получаем:
Теперь нужно сделать одинаковые основания. Мы знаем что 9=3 2 . Воспользуемся формулой степеней (a n ) m = a nm .
Получим 9 х+8 =(3 2 ) х+8 =3 2х+16
3 3х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.
3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.
Смотрим следующий пример:
2 2х+4 — 10•4 х = 2 4
В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (a n ) m = a nm .
4 х = (2 2 ) х = 2 2х
И еще используем одну формулу a n • a m = a n + m :
2 2х+4 = 2 2х •2 4
Добавляем в уравнение:
2 2х •2 4 — 10•2 2х = 24
Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 2 2х ,вот и ответ — 2 2х мы можем вынести за скобки:
2 2х (2 4 — 10) = 24
Посчитаем выражение в скобках:
2 4 — 10 = 16 — 10 = 6
Все уравнение делим на 6:
Представим 4=2 2 :
2 2х = 2 2 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.
9 х – 12*3 х +27= 0
Преобразуем:
9 х = (3 2 ) х = 3 2х
Получаем уравнение:
3 2х — 12•3 х +27 = 0
Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены. Число с наименьшей степенью заменяем:
Тогда 3 2х = (3 х ) 2 = t 2
Заменяем в уравнении все степени с иксами на t:
t 2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t1 = 9
t2 = 3
Возвращаемся к переменной x.
3 х = 9
3 х = 3 2
х1 = 2
Один корень нашли. Ищем второй, из t2:
t2 = 3 = 3 х
3 х = 3 1
х2 = 1
Ответ: х1 = 2; х2 = 1.
На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.
Видео:Сокращаем дроби со степенями №2. Алгебра 8 класс.Скачать

Формулы степеней и корней.
Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.
Число c является n-ной степенью числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием их показатели складываются:
2. В делении степеней с одинаковым основанием их показатели вычитаются:
3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
(abc…) n = a n · b n · c n …
4. Степень дроби равняется отношению степеней делимого и делителя:
5. Возводя степень в степень, показатели степеней перемножают:
Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.
Операции с корнями.
1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:
2. Корень из отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень довольно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и в тоже время возвести в n-ую степень подкоренное число, то значение корня не поменяется:
5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n-ой степени из подкоренного числа, то значение корня не поменяется:
Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:
Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m 4 :a 7 = a 4 — 7 = a -3 .
Чтобы формула a m :a n =a m — n стала справедливой при m=n, нужно присутствие нулевой степени.
Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.
Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n, необходимо извлечь корень n–ой степени из m-ой степени этого числа а:
Видео:Уравнение четвертой степениСкачать

Формулы степеней.
6. a — n = 
7. 
8. a 1/n = 
Видео:Математика| СтепениСкачать

Как сокращать алгебраические дроби?
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Решение показательных неравенств шаг за шагомСкачать

Определение
Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:
Алгебраическая дробь содержит буквенные множители и степени.
Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.
Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.
Видео:11 класс, 3 урок, Уравнения высших степенейСкачать

Сокращение алгебраических дробей
Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.
Если в 7 классе только и разговоров, что об обыкновенных дробях, то 8 класс сокращает исключительно алгебраические дроби.
Сокращение дробей с буквами и степенями проходит в три этапа:
- Определите общий множитель.
- Сократите коэффициенты.
- Поделите все числители и все знаменатели на общий множитель.
Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:
Пример сокращения дроби со степенями и буквами:
- Следуя формуле сокращения степеней в дробях, сокращаем x 3 и x 2
- Всегда делим на наименьшее значение в степени
- Вычитаем: 3 — 1
Получаем сокращенную дробь.
Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.
| ❌ Так нельзя | ✅ Так можно |
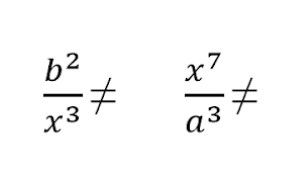 |  |
Примеры сокращения алгебраических дробей с одночленами:
Пример сокращения №1.
- Общий множитель для числителя и знаменателя — 8.
- Х и x 2 делим на x и получаем ответ.
Получаем сокращенную алгебраическую дробь.
Пример сокращения №2.
- Общий множитель для числителя и знаменателя — 7.
- b 3 и b делим на b.
- Вычитаем: 3 — 1 и получаем ответ.
Получаем сокращенную дробь.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Сокращение алгебраических дробей с многочленами
Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:
- сокращайте многочлен в скобках только с таким же многочленом в скобках;
- сокращайте многочлен в скобках целиком — нельзя сократить одну его часть, а другую оставить. Не делайте из многочленов одночлены.
| ❌ Так нельзя | ✅ Так можно |
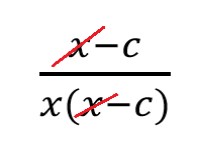 | 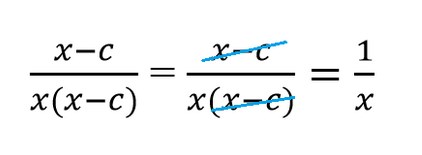 |
Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.
Примеры сокращения алгебраических дробей с многочленами:
Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).
Сокращаем многочлены a+b (в дроби их 3). Многочлен в числителе стоит в квадрате, поэтому мысленно оставляем его при сокращении.
Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Вынесение общего множителя при сокращении дробей
При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.
Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:
- Найдите число, на которое делятся числа каждого одночлена.
- Найдите повторяющиеся буквенные множители в каждом одночлене.
- Вынесите найденные буквенные множители за скобку.
- Далее работаем с многочленом, оставшимся в скобках.
Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.
| Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен. |
Пример 1.
- Выносим общий множитель 6
- Делим 42/6
- Сокращаем получившиеся одинаковые многочлены.
Пример 2.
Как решаем: выносим общий множитель a за скобки и сокращаем оставшиеся в скобках многочлены.
Видео:Сократить дробь алгебра 8 классСкачать

Сокращение дробей. Формулы сокращенного умножения
Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.
Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.
| Квадрат суммы | (a+b) 2 = a 2 + 2ab + b 2 |
| Квадрат разности | (a-b) 2 = a 2 — 2ab — b 2 |
| Разность квадратов | a 2 – b 2 = (a – b)(a+b) |
| Куб суммы | (a+b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 |
| Куб разности | (a-b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3 |
| Сумма кубов | a 3 + b 3 = (a + b)(a 2 — ab+b 2 ) |
| Разность кубов | a 3 — b 3 = (a — b)(a 2 + ab+b 2 ) |
Примеры сокращения дробей с помощью формул сокращенного умножения:
Применяем формулу квадрата разности (a-b) 2 = a 2 — 2ab — b 2 и сокращаем одинаковые многочлены.
Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.
Примеры сокращения дробей за 7 и 8 классы
Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.
- Чтобы сократить дробь, найдите общий множитель числителя и знаменателя.
- Поделите числитель и знаменатель на общий множитель.
- Чтобы разделить многочлен на множители, вынесите общий множитель за скобку.
- Второй способ разделить многочлен на множители — применить формулы сокращенного умножения.
- Выучите все формулы сокращенного умножения — они помогут легко преобразовывать выражения и экономить время при решении задач.
- Можно забыть свое имя, но формулу разности квадратов помнить обязательно — она будет встречаться чаще других.
- Всегда проверяйте результат сокращения: алгебра — точна, коварна и не любит давать вторые шансы.
Возможно тебе будет полезно — Формулы сокращённого умножения (ФСУ)
🌟 Видео
Как решать уравнения четвёртой степени. Формула Феррари | #БотайСоМной #026 | Борис ТрушинСкачать

Как решать уравнения 4 степени Решите уравнение четвертой степени Разложить на множители Безу столбиСкачать

397 Алгебра 9 класс. Степень УравненияСкачать

Как решать уравнения с дробью? #shortsСкачать

Алгебра 7 класс №1 Контрольная работа В-1 К-4 сократите дробьСкачать

Корни n-й степени. Вебинар | МатематикаСкачать

Можно ли решить уравнение 5-й степени? – математик Алексей Савватеев | НаучпопСкачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Алгебра 8. Урок 2 - Сокращение дробейСкачать

Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Как решают уравнения в России и СШАСкачать

Как решать уравнения высших степеней, очень лёгкий способ!!!Скачать