Метод узловых и контурных уравнений онлайн калькулятор (4 видео)

Содержание

Расчет цепи постоянного тока
Рассчитайте схему цепи
Добавьте элементы в цепь
На схеме цепи постоянного тока:
Или откройте сохраненную схему
Где учитесь?
Метод узловых и контурных уравнений онлайн калькулятор
Расчёт электрических цепей онлайн
Методы расчёта
Расчёт по закону Ома
Расчёт по законам Кирхгофа
Рекомендуемые записи
🎦 Видео

Видео:Метод узловых и контурных уравненийСкачать

Расчет цепи постоянного тока

Здесь Вы сможете произвести расчет схемы постоянного тока (Работает, как программа. Для линейных и разветвленных цепей. Рассчитываются токи в электрической цепи. Если нужно что-то другое, то пишите, мы обязательно рассмотрим Ваше предложение).

Видео:Метод контурных токов - определение токов. ЭлектротехникаСкачать

Рассчитайте схему цепи

Выполните расчет цепи постоянного тока или сохраните схему цепи, чтобы потом была возможность начать с того места, на чем закончили (для этого воспользуйтесь кнопками, расположенными ниже ‘Рассчитать схему’ или ‘Сохранить схему’).

Видео:Законы Кирхгофа. Метод контурных уравненийСкачать

Добавьте элементы в цепь

Тип элемента:

Короткое название:

Величина:

Важно

Чтобы добавить элемент в электрическую цепь, необходимо ввести тип элемента (например, резистор), указать краткое наименование элемента (например, R1 — для того, чтобы легче ориентироваться), также укажите величину (например, для резистора R1 — это 4 Ом — но, нужно ввести безразмерно, т.е. ввести 4)

На схеме цепи постоянного тока:

Видео:Метод узловых потенциалов - определение токов. ЭлектротехникаСкачать

Или откройте сохраненную схему

Чтобы открыть схему цепи — нажмите на кнопку ‘Открыть схему’ (см. ниже).
Пример файла, скачать

Видео:Метод узловых потенциалов. Самое простое и понятное объяснение этого методаСкачать

Где учитесь?

Для правильного составления решения, укажите:

Видео:решение задачи составлением уравнений по правилам киргофа. Законы киргофа кратко на практикеСкачать

Метод узловых и контурных уравнений онлайн калькулятор

не работает пишет удалите неиспользованные компоненты хотя все соединено

Не работает ошибка! Значения элемента

Пожалуйста, пришлите скрин вашей схемы на admin@electrikam.com.

Почему пишет,что в схеме отсутствует эдс хотя я его поставит

Пожалуйста, пришлите скрин вашей схемы на admin@electrikam.com.

Ошибка! В ветви отсуствует сопротивление: R

В ветви должно быть хотя бы одно сопротивления

Видео:Расчет электрической цепи постоянного тока методом узловых и контурных уравненийСкачать

Расчёт электрических цепей онлайн

На сайте появилась программа для расчёта установившихся режимов электрических цепей по законам ТОЭ. На настоящий момент реализованы методы расчёта по законам Ома, по законам Кирхгофа, по методу узловых потенциалов, методу контурных токов, методу эквивалентного генератора. Также программа позволяет рассчитать эквивалентное сопротивление цепи относительно источника питания. Программа позволяет нарисовать схему, задать параметры её элементов и рассчитать схему. В результате формируется текстовое описание порядка расчёта, рассчитывается баланс мощностей и строятся векторные диаграммы.

Рисование схемы производится путём перетаскивания элементов методом drag-and-drop из боковой панели и последующим соединением выбранных элементов.

В боковой панели доступны следующие элементы с задаваемыми параметрами:

резистор :
- номер элемента;
- сопротивление, Ом;
конденсатор :
- номер элемента;
- сопротивление, Ом;
катушка индуктивности :
- номер элемента;
- сопротивление, Ом;
источник ЭДС :
- номер элемента;
- амплитудное значение, В;
- начальная фаза, °;
источник тока :
- номер элемента;
- амплитудное значение, В;
- начальная фаза, °.

Инструкция по применению программы приведена здесь.

Методы расчёта

После завершения рисования схемы при нажатии кнопки «Расчёт» запускается расчёт электрической цепи. Программа анализирует исходную схему и при выявлении каких-либо ошибок сообщает об этом. При успешном анализе схемы запускается расчёт по методам ТОЭ.

Расчёт по закону Ома

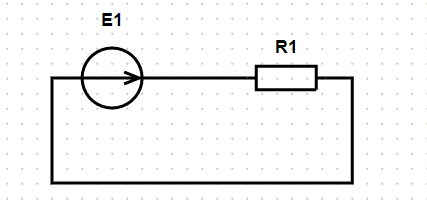
Расчёт по закону Ома осуществляется для одноконтурных схем. Используемая методика расчёта приведена здесь.

Пример схемы и расчёт:

Исходные данные и схема:

E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза: 0
R1:
- Номер элемента: 1
- Сопротивление, Ом: 1

После нажатия кнопки «Расчёт» формируется решение:

В исходной схеме только один контур. Рассчитаем её по закону Ома.

Согласно закону Ома, ток в замкнутой цепи равен отношению ЭДС цепи к сопротивлению. Составим уравнение, приняв за положительное направление тока $ underline $ направление источника ЭДС $ underline_ $:

$$ R_cdot underline = underline_ $$

Подставим в полученную систему уравнений значения сопротивлений и источников и получим:

Отсюда искомый ток в цепи равен

$$ underline = 100space textrm$$

Расчёт по законам Кирхгофа

Для многоконтурных схем расчёт осуществляется по законам Кирхгофа. Используемая методика расчёта приведена здесь.

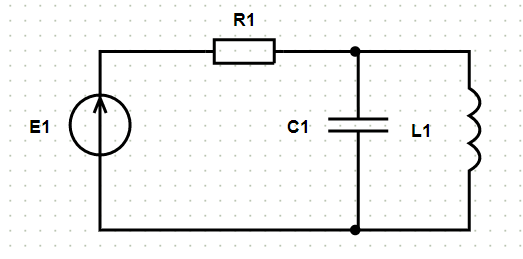
Пример схемы и расчёт:

Исходные данные и схема:

E1:
Номер элемента: 1
Амплитудное значение: 100 В
Начальная фаза: 0
R1:
Номер элемента: 1
Сопротивление, Ом: 1
L1:
Номер элемента: 1
Сопротивление, Ом: 1
C1:
Номер элемента: 1
Сопротивление, Ом: 1

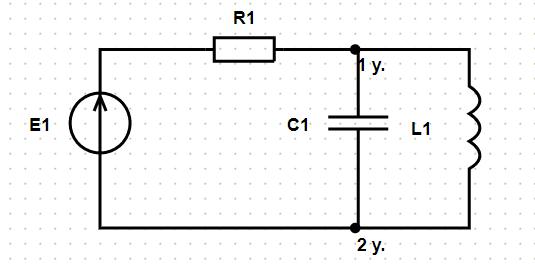
После нажатия кнопки «Расчёт» на исходной схеме появляется нумерация узлов и формируется решение:

Рассчитаем схему по законам Кирхгофа.

В данной схеме: узлов − 2 , ветвей − 3, независимых контуров − 2.

Произвольно зададим направления токов в ветвях и направления обхода контуров.

Принятые направления токов:
Ток $ underline_ $ направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы $ underline_ $, $ R_ $.
Ток $ underline_ $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ L_ $.
Ток $ underline_ $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ C_ $.

Принятые направления обхода контуров:
Контур №1 обходится через элементы $ underline_ $, $ R_ $, $ L_ $ в указанном порядке.
Контур №2 обходится через элементы $ L_ $, $ C_ $ в указанном порядке.

Составим уравнения по первому закону Кирхгофа. При составлении уравнений «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» − со знаком «−».

Количество уравнений, составляемых по первому закону Кирхгофа, равно $ N_textrm − 1 $, где $ N_textrm $ − число узлов. Для данной схемы количество уравнений по первому закону Кирхгофа равно 2 − 1 = 1.

Составим уравнение для узла №1:

$$ underline_ − underline_ − underline_ = 0 $$

Составим уравнения по второму закону Кирхгофа. При составлении уравнений положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура.

Количество уравнений, составляемых по второму закону Кирхгофа, равно $ N_textrm − N_textrm + 1 $, где $ N_textrm $ — число ветвей. Для данной схемы количество уравнений по второму закону Кирхгофа равно 3 − 2 + 1 = 2.

Составим уравнение для контура №1:

$$ R_cdot underline_ + jX_cdot underline_=underline_ $$

Составим уравнение для контура №2:

$$ jX_cdot underline_ − (−jX_)cdot underline_=0 $$

Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми токами. Система уравнений по законам Кирхгофа для исходной цепи выглядит следующим образом:

$$ beginunderline_ − underline_ − underline_ = 0 \ R_cdot underline_+jX_cdot underline_ = underline_ \ jX_cdot underline_−(−jX_)cdot underline_ = 0 \ end $$

Подставим в полученную систему уравнений значения сопротивлений и источников и получим:

$$ beginunderline_ − underline_ − underline_=0 \ underline_+ j cdot underline_=100 \ j cdot underline_+ j cdot underline_=0 \ end $$

Решим систему уравнений и получим искомые токи: