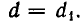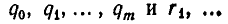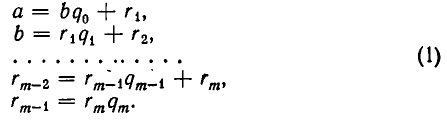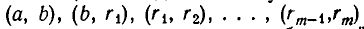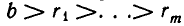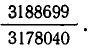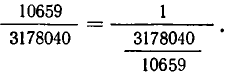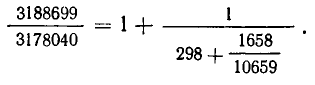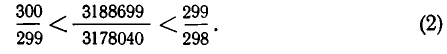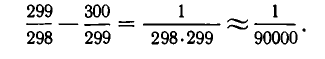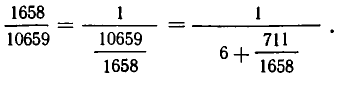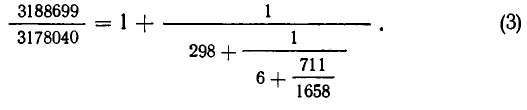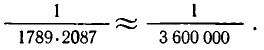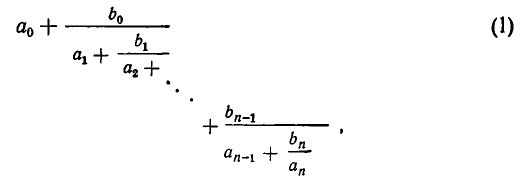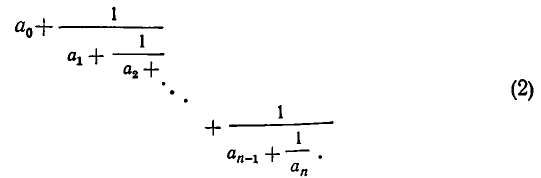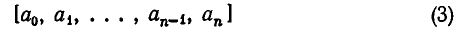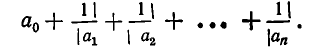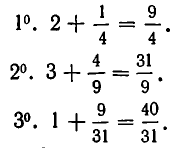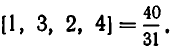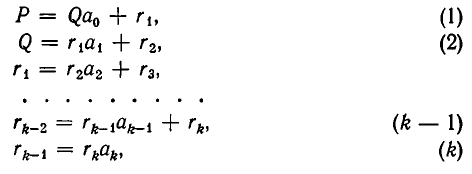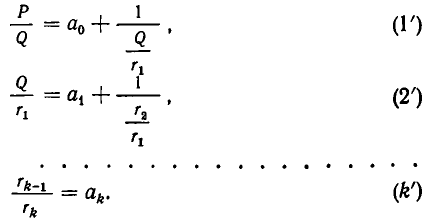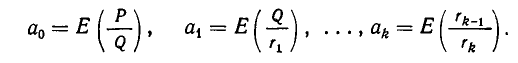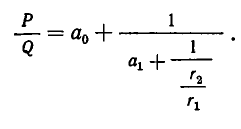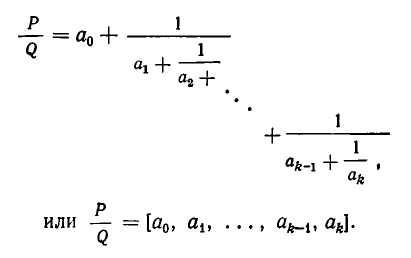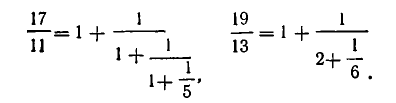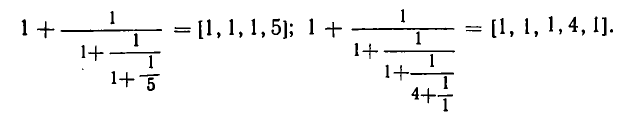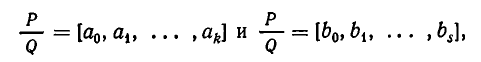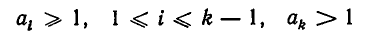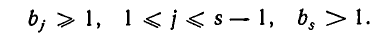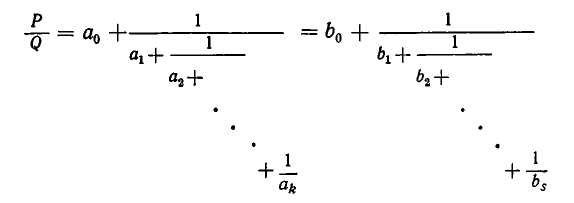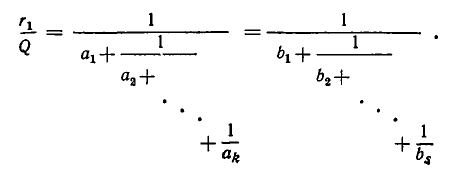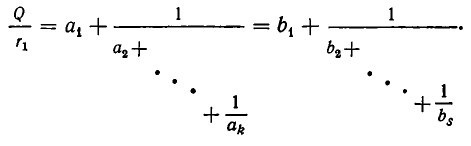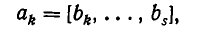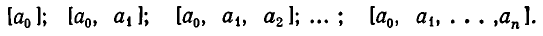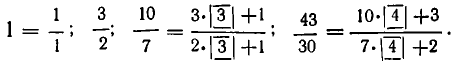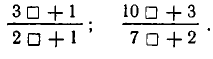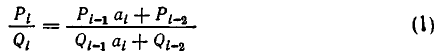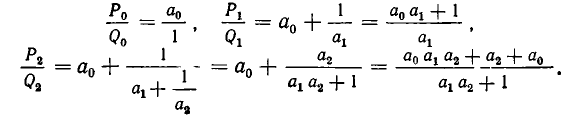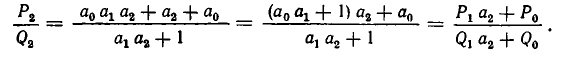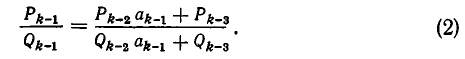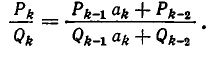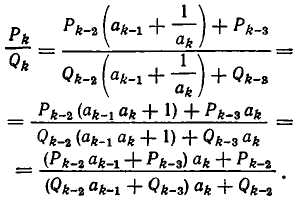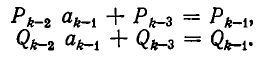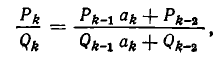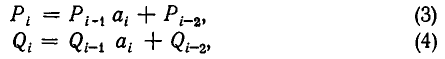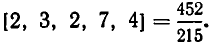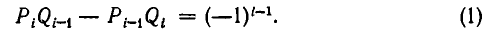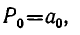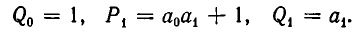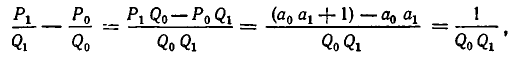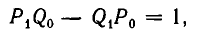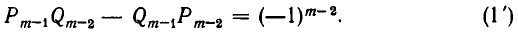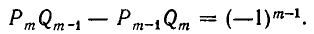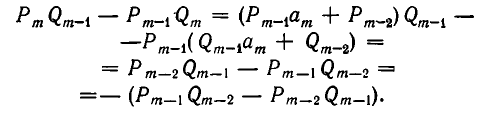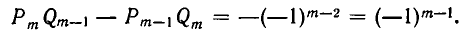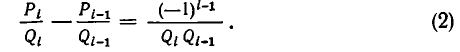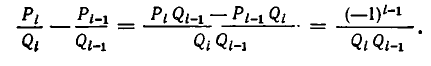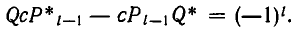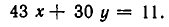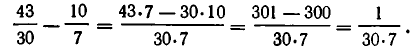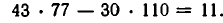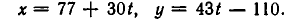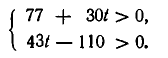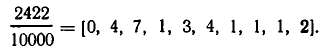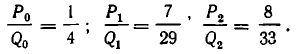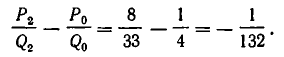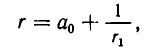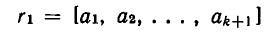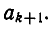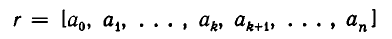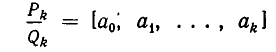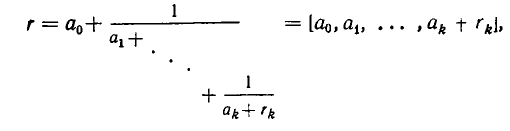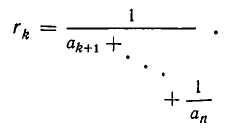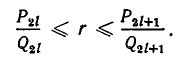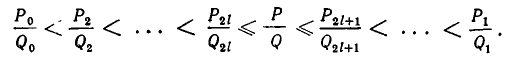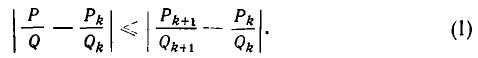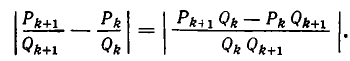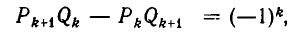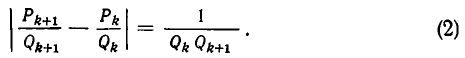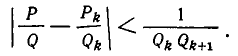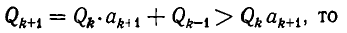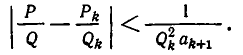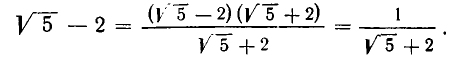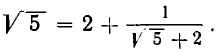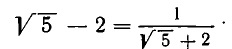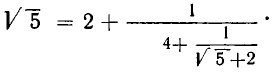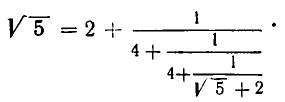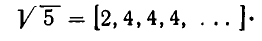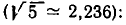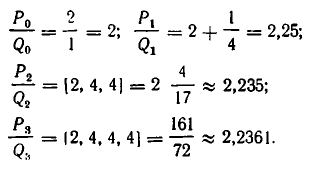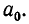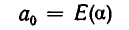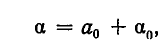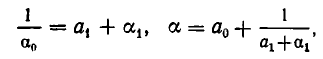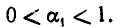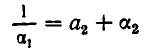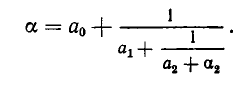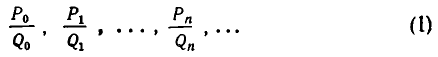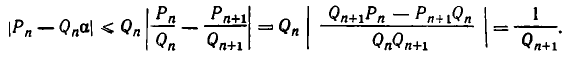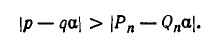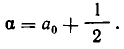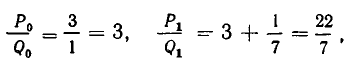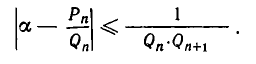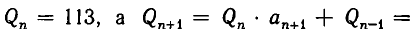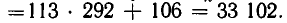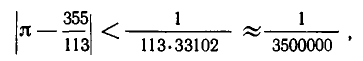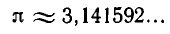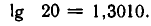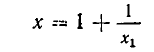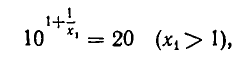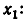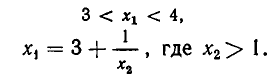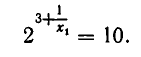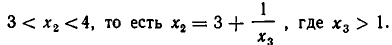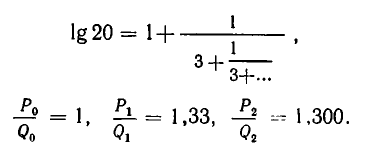- Цепные дроби и диофантовы уравнения
- Линейное диофантово уравнение и 4 способа его решения
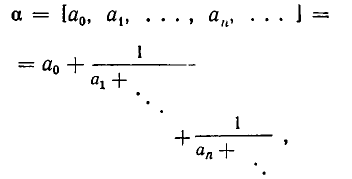
- Непрерывная дробь (цепная дробь) в математике с примерами решения и образцами выполнения
- Конечные цепные дроби
- Пример цепной дроби
- Определение цепной дроби
- Представление рациональных чисел в виде конечной цепной дроби
- Подходящие дроби
- Свойства подходящих дробей
- Диофантовы уравнения первой степени
- Подходящие дроби и календарь
- Приближение цепной дроби подходящими дробями
- Бесконечные цепные дроби
- Подходящие дроби и наилучшие приближения иррациональных чисел рациональными
- Цепные дроби как вычислительный инструмент
- 🎬 Видео
Видео:18. Метод цепных дробей. Алексей Савватеев. 100 уроков математики 6+Скачать

Цепные дроби и диофантовы уравнения
Автор работы награжден дипломом победителя III степени
Актуальность исследования . Применение аппарата цепных дробей к прикладным задачам, в том числе олимпиадного характера, позволяет углубить математические знания, расширить кругозор и повысить мотивацию к изучению математики. Ведь задачи на оптимизацию, которых много в ЕГЭ, предполагают решение с помощью диофантовых уравнений; также в том пресловутом справочнике прозвучала мысль, что подход Диофанта к решению уравнений особенный, и мне хотелось бы поделиться умением решать диофантовы уравнения с другими. Я предполагаю, что элементы высшей математики могут быть доступны и интересны ученикам средней школы.
Объект исследования: цепные дроби и диофантовы уравнения.
Предмет исследования: применение последовательности подходящих дробей для решения диафантовых уравнений и других задач.
Обработка теоретического материала (его отбор, а также последовательное и доступное изложение);
Поиск областей применения цепных дробей;
Составление практического материала в форме упражнений.
Гипотеза исследования : применение цепных дробей позволяет найти один из способов решения диофантовых уравнений и других задач олимпиадного характера.
Изучить понятие цепных дробей и диофантовых уравнений;
На примерах приближения различных чисел подходящими дробями (рациональные числа, квадратичные иррациональности) понять закономерности использования аппарата цепных дробей;
Ознакомиться с историей возникновения и использования цепных дробей;
Выявить и применить возможности цепных дробей к решению разных видов олимпиадных задач.
Действительные числа однозначно отображаются цепными дробями. Основное значение такого изображения заключается в том, что, зная цепную дробь, изображающую действительное число, можно определить это число с достаточной точностью. Умение решать диофантовы уравнения может пригодиться в реальной жизни, например, задачи на оптимизацию, которые неоднократно встречаются в ЕГЭ; также данное умение окажется как нельзя кстати при решении задач, выходящих за рамки школьной программы, олимпиадных заданий.
Глава 1. Понятие цепных дробей.
Примеры разложений действительных чисел в цепную дробь.
Дробь можно записать в виде суммы целой части и правильной дроби: . Но , а дальше: . Значит, . Далее получим .
Продолжим этот процесс до тех пор, пока не придем к знаменателю . В результате мы представим обыкновенную дробь в виде:
Эйлер назвал дроби такого вида непрерывными. Приблизительно в то же время в Германии появился другой термин – цепная дробь. Так за этими дробями и сохранились оба названия. Ввиду громоздкости развернутой записи цепной дроби применяют компактную запись .
В качестве примера представим дробь в виде цепной дроби:.
Или в компактной форме: [1; 3, 2, 4 ].
Мы познакомились с разложением в цепную дробь обыкновенной дроби, т.е. рационального числа. Любое рациональное число представимо в виде конечной цепной дроби. Конечность следует из алгоритма Евклида. Но в виде цепной дроби можно записать любое действительное число. Только конечными цепными дробями здесь не обойтись. Приведем разложение в непрерывную дробь числа .
и т.д. Видна закономерность.
Т.е. в компактной форме = [1: 2, 2, 2, 2, 2…].
Оказывается, квадратичные иррациональности (т.е. числа вида , где a , b , c — рациональные числа), и только они раскладываются в бесконечные периодические дроби. На этот факт впервые указал Эйлер, строгое его доказательство дал Лагранж.
Если оборвать дробь на знаменателе , то останется дробь . Обращая ее в обыкновенную, получим . Это выражение называют k —й подходящей дробью для исходной цепной дроби.
Например, для нашей дроби имеем:
нулевая подходящая дробь: ,
первая подходящая дробь: ,
вторая подходящая дробь: ,
третья подходящая дробь: . Она равна самому числу.
Для цепной дроби, представляющей число, имеем следующие подходящие дроби:
нулевая подходящая дробь: ,
первая подходящая дробь: ,
вторая подходящая дробь: ,
третья подходящая дробь: и т.д.
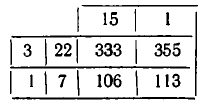
Подходящие дроби удобно вычислять с помощью специальной таблицы. Для этого посмотрим, как вычисляются подходящие дроби:
и т.д. Вообще имеют место рекуррентные соотношения
Эти вычисления удобно производить последующей схеме:
В первой строке этой таблицы записаны недробные элементы, с которых мы начинали строить каждый «этаж», нашей многоэтажной дроби.
Во второй строке сначала записано число 1. Это ключевое число, и надо просто запомнить, что вторая строка начинается с числа 1. Далее записаны числители подходящих дробей.
В третьей строке сначала записано число 0. Это ключевое число, и надо просто запомнить, что третья строка всегда начинается с числа 0.Далее записаны знаменатели подходящих дробей.
Оказывается, что, зная лишь нулевую подходящую дробь, следуя нашим рекуррентным соотношениям, можно найти сколь угодно много числителей и знаменателей в подходящих дробях.
Для получения очередного числителя (знаменателя) необходимо взять элемент того же столбца из первой строки умножить на предыдущий числитель (знаменатель) и прибавить к произведению «предпредыдущий» числитель (знаменатель).
Составим таблицу подходящих дробей для цепной дроби, изображающей число.
При этом, если учесть, что , , , =1,41666, то можно увидеть, что чем дальше мы идем, тем лучшее приближение числа получаем.
Цепные дроби обладают следующим важным свойством: если действительное число x записать в виде непрерывной дроби, то подходящая дробь дает наилучшее приближение числа x среди всех дробей, знаменатели которых не превосходят . Т.е. чем больше k , тем k – подходящая дробь ближе к числу.
В связи с этим замечательным свойством рассмотрим применение цепных дробей в календаре.
Глава 2. Приложения цепных дробей
Календарь и подходящие дроби
Древнеримские жрецы, ведавшие исчислением времени, произвольно удлиняли некоторые года, чтобы согласовать календарные даты с сезонными явлениями природы. Впервые порядок в счете времени навел в I в. до нашей эры римский император Юлий Цезарь. Он постановил считать одни годы по 365 суток, а другие по 366 суток, чередуя их по правилу три года подряд коротких, четвертый – длинный. Гораздо позже, с введением христианского летоисчисления, високосным стали считать каждый год, порядковый номер которого делится на 4. Этот календарь в честь Юлия Цезаря называется юлианским. По нему продолжительность суток составляет 365 суток 6 ч, что больше истинной лишь на 11 мин 14 с. Однако и это решение оказалось неудовлетворительным. К XVI в. ошибка, накапливаясь, составила уже около 10 суток.
Следующую реформу календаря провел Григорий XIII – папа римский. Было решено: сдвинуть числа на 10 дней, оставить чередование простых и високосных лет, при этом, если порядковый номер года оканчивается двумя нулями, но число сотен не делится на 4, то этот год простой. В настоящее время расхождение между юлианским и новым, григорианским календарями составляет 13 дней, поскольку с тех пор накопилось еще три дня (в 1700, 1800 и 1900 гг.). Продолжительность григорианского года составляет
365, 2425 суток, т.е. 365 суток 5 ч 49 мин 12 с, т.е. она больше истинной лишь на 26с. Полученная точность очень велика и вполне достаточна для практических нужд.
Интересная система календаря была предложена среднеазиатским математиком и поэтом Омаром Хайямом (ок.1048-1122), по ней високосными годами должны были считаться 8 лет из каждых 33. Продолжительность года по О. Хайяму составляет 365 суток, его погрешность всего 19с в год.
В 1864 г. русский астроном И. Медлер предложил с XX столетия ввести в России следующую поправку к юлианскому календарю: через каждые 128 лет пропускать один високосный год из 32, которые выпадают на этот период. Этот календарь самый точный из всех перечисленных. Здесь погрешность сокращается всего до 1с. Однако календарь И. Медлера не был принят, видимо, из-за того, что период в 128 лет не является «круглым» числом.
Системы календаря оказываются связанными с записью астрономического года в виде цепной дроби:
Год продолжительностью 365 суток — это нулевая подходящая дробь этой цепной дроби, 365 — юлианский год – первая подходящая дробь, 365, 365 и 365 — вторая, третья и четвертая подходящие дроби. А именно:
Системой, соответствующей второй подходящей дроби: семь високосных лет из 29, никто не предложил воспользоваться, видимо, потому, что третья подходящая дробь ненамного сложнее, а точность ее гораздо больше (вспомним, что это система О. Хайяма), а четвертой подходящей дроби соответствует система И. Медлера.
Второе свойство цепных дробей
Вспомним, как вычисляются подходящие дроби.
и т.д. Имеют место рекуррентные соотношения
Второе свойство цепных дробей: для любого k = 1,2,…, n имеет место формула
Диофантовы уравнения вида ax+ by =с с использованием цепных дробей.
Используем отмеченное нами свойство цепных дробей для решения уравнения ax+ by = c Коэффициенты a и b взаимно просты. Разложим в цепную дробь. При этом .
Поскольку обе дроби несократимы, то a = P n , b = Qn . По свойству имеем
Умножив обе части этого равенства на (-1) n c , получим
Общее решение запишется в виде:
Решим уравнение 17х + 13у = 5.
Поскольку , то n = 2, ,откуда х0 = -5•3 = -15, у0= 4•5 = 20 и общее решение имеет вид
При решении уравнений вида ax + by = c будем использовать следующий алгоритм :
1) Разложим в цепную дробь (с помощью алгоритма Евклида или с помощью соответствующих преобразований).
2) Из разложения =определяем значение n (т.е. длину цепной дроби).
3) Находим n -1 – подходящую дробь (в случае необходимости используем таблицу).
4) Применяем формулы:
1) Можно находить сначала частное решение:
Глава 3. Диофантовы уравнения
Диофантовыми уравнениями называются алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, для которых надо найти целые или рациональные решения. При этом число неизвестных в уравнениях должно быть не менее двух. Диофантовы уравнения имею, как правило, много решений, поэтому их называют неопределенными уравнениями. К диофантовым уравнениям приводят задач, по смыслу которых неизвестные значения величин могут быть только целыми числами. В качестве примера задача на составления диофантовых уравнений, может служить задача о размере рубля монетами достоинством в 1; 2; 3; 5; 10; 15 и 50 копеек. Соответствующее уравнение имеет вид:
Решить такое уравнение – это значит найти все такие наборы.
Число наборов, удовлетворяющих этому уравнению примерно равно
510 * 10 7 . Названы эти уравнения по имени греческого математика. Его книга «Арифметика» содержала большое количество интересных задач, его изучали математики всех поколений. Книга сохранилась до наших дней, её можно найти в русском переводе в библиотеке. К диофантовым уравнениям приводят задачи, по смыслу которых неизвестные значения величин могут быть только целыми числами.
Для линейных уравнений с двумя неизвестными, т.е. уравнение вида
ax + by = c , где a , b , c – целые числа, а x , y – целочисленные решения уравнения. для данного уравнения справедливы следующие утверждения:
Если коэффициенты a и b уравнения ax + by = c являются взаимно простыми числами (их наибольший общий делитель d =1), то это уравнение имеет, по крайней мере, одно целочисленное решение.
Если d ≠1, то уравнение ax + by = c не имеет целочисленных решений.
Если d =1/ то уравнение ax + by = c имеет бесконечное множество целочисленных решений, которые задаются формулами х = α + bt , y = β – at ,
Где ( α ; β ) – некоторое целочисленное решении уравнения ax + by = c , at t – произвольное целое число.
Долгое время надеялись отыскать общий решения любого диофантова уравнения. Однако в 1970 году ленинградский математик Ю.В. Матиясевич доказал, что такого общего способа быть не может.
Рассмотрим решение системы диофантовых уравнений первой степени на конкретном примере:
Решить в целых числах систему уравнений:
Решение: вычтем из второго уравнения первое, получим yz — y — z =5
или ( y -1)( z -1)=6. Число 6 можно разложить на целые множители четырьмя способами:
Эти системы дают тройки значений
( x ; y ; z ): (5;2;7), (5;7;2), (7;4;3), (7;3;4), (19;-5;0), (17;-2;-1), (17; -1;-2).
Диофантовы уравнения решаются методом перебора (один из самых древнейших методов решения математических задач, возникающих на практике).
А также нужно помнить, что если число d есть наибольший делитель целых чисел a и b , то существует такие числа k и 1, что d = ka + lb . Алгоритм Евклида позволяет вычислить целые числа k и 1.
Линейное диофантово уравнение ax + by = c не будет иметь решений, если числа с и d взаимно простые. Если число с кратно числу d , то одно из решений уравнения будет иметь вид: x = pk и y = pl .
Если целое число c делится на D ( a ; b ), то уравнение ax + by = c имеет целые решения (если некоторые из чисел a , b и с отрицательны, то вместо них берем их модули).
Рассмотрим, как искать эти решения на следующем примере:
Это уравнение может иметь целые решения, так как D (28;40)=4, а число 60 делится на цело, на 4. Ясно, что любое целое решение уравнения 28 x – 40 y =60 удовлетворяют и уравнению 7 x – 10 y = 15 из заданного сокращения обеих частей на 4. Обратно любое целое решение уравнения 7 x – 10 y = 15, является и целым решением заданного уравнения. У получившегося после сокращения на 4 уравнение 7 x – 10 y = 15 коэффициенты при неизвестных взаимно просты, т.е. D (7;10) равно 1.
Применим к этим коэффициентам алгоритм Евклида. Мы видим, что при делении числа 7 на 3 получилось неполное частное 2 и остаток 1, а потому 7 = 2*3 + 1. Значит 1=7-2*3. таким же путем устанавливаем, что 10=1*7+3, а потому 3=10-1*7. Подставляя это выражение в равенство 1=7-2*3, получаем 1=7-2(10-1*7). Раскрывая скобки, получаем x =3 и y =2 дают целые решения уравнения 7 x – 10 y = 15. Чтобы получить целые решения уравнения 7 x – 10 y = 15, надо оба этих числа умножить на 15. Таким путем мы получим одно решение уравнения
Другие целые решения того же уравнения имеют вид: х=45+10 t , y =30 + 7 t , где t – любое число.
Чтобы выделить целые неотрицательные решения заданного уравнения, надо найти такие значения t , при которых 45 +10 t >0 и 30+7 t >0. Из этих неравенств находим, что должны выполняться условия t >-4,5, t >-30/7, из которых вытекает, что t >-4.
Итак, данное уравнение имеет бесконечно много целых неотрицательных решений, задаваемых формулами х=45+10 t , y =30 + 7 t , где t принимает значение -4, -3,-2, …
Часть 4. Применение теории на практике
x^2 + y^2 – 2x + 4y=-5
В левой части уравнения выделим полный квадрат:
x^2 – 2x + 1 + y^2 + 4y + 4=0
Сумма квадратов равна 0 лишь в одном случае
Решив систему, получим, что x= 1, y= -2
x^2 – 6x + y^2 + 6y + 18=0
Докажем, что это уравнение имеет единственное целочисленное решение.
В левой части уравнения выделим полные квадраты :
( x – 3 )^2 + ( y + 3 )^2=0
Данное уравнение имеет решение, когда
Теперь я предлагаю рассмотреть графический метод решения диофантовых уравнений.
Алгоритм построения графика уравнения ах + by + с = 0:
1. Придать переменной х конкретное значение х= х1; найти из уравнения ах1 + by + c = 0 соответствующее значение y =y1.
2. Придать переменной х другое значение х=х2; найти из уравнения ах2 + by + c = 0 соответствующее значение y =y2.
3. Построить на координатной плоскости х Oy две точки (х1;у1) и (х2;у2).
4. Провести через эти две точки прямую – она и будет графиком уравнения ах + by + с = 0.
Необходимо найти все пары (х, у) целых чисел, удовлетворяющих системе неравенств:
Рассмотрим на координатной плоскости области, которые описываются заданными неравенствами. А затем выберем в них лишь точки с целочисленных координат х, у.
Получаем два случая:
1) Неравенство (1) путем выделения полных квадратов сводится к условию
2) Неравенство (2) сводится к виду
Единственной точкой, принадлежащей одновременно двум кругам, будет точка М( 12; -8). Это выясняется подстановкой в систему числовых значений координат всех узлов квадратной сетки, соседних с точкой М.
Пример 1. Для перевозки большого количества контейнеров по 170 кг и по 190 кг выделены трехтонные машины. Можно ли ими загружать машины полностью?
Решение. пусть х и у количество контейнеров по 170 и 190 кг соответственно, тогда имеем уравнение
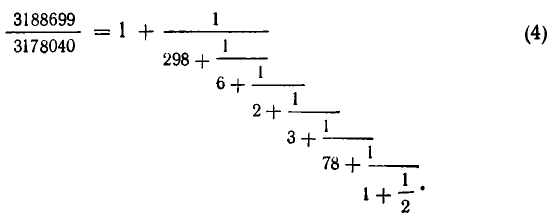
Для нахождения частного решения воспользуемся разложением дроби в цепную дробь
Свернув предпоследнюю подходящую к ней дробь в обыкновенную
Частное решение данного уравнения имеет вид:
х 0 = (-1) 4 300∙9=2700, у 0 =(-1) 5 300∙8= -2400,
а общее задается формулой х=2700 — 19k, y= — 2400 + 17k.
откуда получаем условие на параметр k: 141 ≤ k ≤ k=142, x=2, y=14.
Пример 2. Разложить в цепную дробь .
Решение. Находим: a0=1, . Поскольку , будем иметь a1=a0=1, так что и так далее, то есть
Задания для самостоятельного решения
Пример 1. Найти значение следующих цепных дробей:
Пример 2. Найти значение цепной дроби .
Пример 3. Решить в целых числах уравнение 54х + 37у = 1.
Подведем итоги. В ходе исследования была проведена следующая работа:
1)Собран и освоен теоретический материал, составлены на основании изученных свойств алгоритм решения приведенных в данной работе диофантовых уравнений. Сформулированы замечания, использующиеся при решении данных уравнений.
2)Найдены некоторые области применения цепных дробей.
3)Составлены и выполнены практические задания по разложению действительных чисел в цепные дроби, а также по решению диофантовых уравнений вида ax + by = c , других олимпиадных задач.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Баврин И.И.,Фрибус Е.А. Занимательные задачи по математике.- М.: Гуманитарный издательский центр ВЛАДОС, 1999.- 208 с.
Басова Л.А., Шубин М.А., Эпштейн Л.А. Лекции и задачи по математике.- М.: Просвещение, 1981.- 96 с.
Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. За страницами учебника математики: Арифметика. Алгебра. Геометрия: Книга для учащихся 10-11 кл. общеобразовательных учреждений.- М.: Просвещение, 1996.- 320 с.
Ожигова Е. П. Что такое теория чисел.- М.: Знание, 1970.- 96 с.
Пичурин Л. Ф. За страницами учебника алгебры: Книга для учащихся 7-9 кл.сред.шк.- М.: Просвещение, 1990.- 224 с.
Савин А. П. Энциклопедический словарь юного математика.- М.: Педагогика, 1989.- 352 с.
Хинчин А. Я. Цепные дроби.- М.: Наука, 1978.- 112 с.
Видео:Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Линейное диофантово уравнение и 4 способа его решения
Разделы: Математика
Првило 1. Если с не делится на d, то уравнение ах + ву = с не имеет решений в целых числах. Н.О.Д.(а,в) = d.
Правило 2. Чтобы найти решение уравнения ах + ву = с при взаимно-простых а и в, нужно сначала найти решение (Хо ; уо) уравнения ах + ву = 1; числа СХо , Суо составляют решение уравнения ах + ву = с.
Решить в целых числах (х,у) уравнение
Первый способ. Нахождение частного решения методом подбора и запись общего решения.
Знаем, что если Н.О.Д.(а;в) =1, т.е. а и в взаимно-простые числа, то уравнение (1)
имеет решение в целых числах х и у. Н.О.Д.(5;8) =1. Методом подбора находим частное решение: Хо = 7; уо =2.
Итак, пара чисел (7;2) — частное решение уравнения (1).
Значит, выполняется равенство: 5 x 7 – 8 x 2 = 19 … (2)
Вопрос: Как имея одно решение записать все остальные решения?
Вычтем из уравнения (1) равенство (2) и получим: 5(х -7) – 8(у — 2) =0.
Отсюда х – 7 = 

Тем самым все целые решения исходного уравнения можно записать в таком виде:


Второй способ. Решение уравнения относительно одного неизвестного.
Решаем это уравнение относительно того из неизвестных, при котором наименьший (по модулю) коэффициент. 5х — 8у = 19 


Остатки при делении на 5: 0,1,2,3,4. Подставим вместо у эти числа.
Если у = 0, то х = 

Если у =1, то х = 

Если у = 2, то х = 


Если у =3, то х = 

Если у = 4 то х = 

Итак, частным решением является пара (7;2).
Тогда общее решение: 

Третий способ. Универсальный способ поиска частного решения.
Для решения применим алгоритм Евклида. Мы знаем, что для любых двух натуральных чисел а, в, таких, что Н.О.Д.(а,в) = 1 существуют целые числа х,у такие, что ах + ву = 1.
1. Сначала решим уравнение 5m – 8n = 1 используя алгоритм Евклида.
2. Затем найдем частное решение уравнения (1)по правилу 2.
3. Запишем общее решение данного уравнения (1).
1. Найдем представление: 1 = 5m – 8n. Для этого используем алгоритм Евклида.
8 = 5 
5 = 3
3 = 2 
Из этого равенства выразим 1. 1 = 3 — 2 


= 3 — 5 




= 5
2. Частное решение уравнения (1): Хо = 19m; уо =19n.
Отсюда получим: Хо =19

Пара (-57; -38)- частное решение (1).
3. Общее решение уравнения (1): 

Четвертый способ. Геометрический.
1. Решим уравнение 5х – 8у = 1 геометрически.
2. Запишем частное решение уравнения (1).
3. Запишем общее решение данного уравнения (1).
Отложим на окружности последовательно друг за другом равные дуги, составляющие

На 5 – ом шаге получили вершину, соседнюю с начальной, при этом сделали 3 полных оборота и еще прошли 



Итак, Хо = 5, уо =3 является частным решением уравнения 5х – 8у = 1.
2. Частное решение уравнения (1): Хо = 19 
3. Общее решение уравнения (1): 

Видео:Вебинар: Решение линейных уравнений в целых числах. Метод цепных дробейСкачать

Непрерывная дробь (цепная дробь) в математике с примерами решения и образцами выполнения
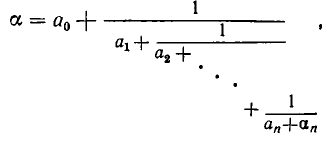
Непрерывная дробь (или цепная дробь) — это конечное или бесконечное математическое выражение вида. где. есть целое число, а все остальные. — натуральные числа (положительные целые). При этом числа. называются неполными частными или элементами цепной дроби.
Видео:РЕШАЕМ ДИОФАНТОВОЕ УРАВНЕНИЕ | ПРОСТЫМИ СЛОВАМИСкачать

Конечные цепные дроби
В арифметике часто приходится искать наибольший общий делитель двух натуральных чисел. В младших классах эту задачу решают с помощью разложения чисел на простые множители. Однако этот способ в школе не получает теоретического обоснования, так как он опирается на не доказываемую (а часто и не формулируемую ) довольно трудную теорему о существовании и единственности разложения натуральных чисел на простые множители.
Другой метод решения этой задачи, свободный от указанного недостатка, изложен еще в книге Евклида «Начала» (III век до н. э.); его называют алгоритмом Евклида или способом последовательного деления. Изложим этот способ.
Напомним сначала некоторые свойства деления с остатком. Пусть а — целое число и b — натуральное число. Существуют такие целые числа q (частное) и r (остаток), что 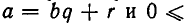
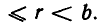
Справедливо следующее утверждение: если а = bq + r, то наибольший общий делитель чисел а и b совпадает с наибольшим общим делителем чисел b и r.
В самом деле, обозначим наибольший общий делитель чисел а и b через d, а наибольший общий делитель чисел b и r — через 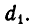
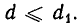
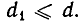
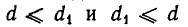
Теперь опишем алгоритм Евклида. Он заключается в том, что для целого числа а и натурального числа b последовательно находят две конечные последовательности чисел 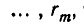
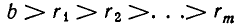
Тогда 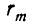
совпадают друг с другом. Но 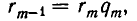
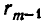
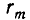
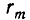
Заметим, что цепь равенств (1), выражающая алгоритм Евклида, не может быть бесконечной, так как из
вытекает, что в (1) не более чем b равенств.
Пример цепной дроби
В некоторых приложениях математики встречаются очень громоздкие дроби. Возникает вопрос, нельзя ли подобрать дробь со сравнительно небольшим знаменателем, достаточно близкую к данной громоздкой дроби. Аппаратом для решения этой задачи являются дроби особого вида, называемые цепными или непрерывными дробями.
Прежде чем излагать общую теорию цепных дробей, рассмотрим следующий пример. Отношение экваториального радиуса Земли к ее полярному радиусу выражается дробью
Попробуем упростить эту дробь. Для этого сначала выделим из нее целую часть: 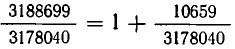
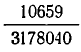
В знаменателе получившейся дроби снова выделим целую часть:
Это выражение позволяет получить хорошее приближение для рассматриваемой дроби. Ясно, что при отбрасывании в знаменателе дробной части 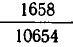
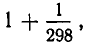
больше, чем наша дробь. Если же округлить знаменатель в сторону увеличения, то мы получим дробь 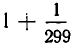
Разность полученных приближений 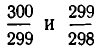
Значит, как 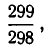
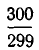
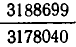
Если мы хотим получить еще лучшее приближение, надо аналогичным образом преобразовать отброшенную дробную часть
Подставляя это выражение в (1), получаем:
Ясно, что дробь 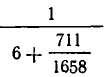
Поэтому получаем для 
или, преобразуя дроби,
Получились оценки с большими знаменателями, чем в (2). Но их точность существенно выше — погрешность полученных приближений не больше, чем
Продолжая описанный процесс, мы получим в конце концов точное выражение для 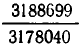
Разумеется, полученная дробь менее удобна, чем 
Определение цепной дроби
Введем следующее общее определение:
Всякое выражение вида
где 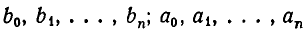
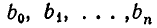
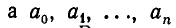
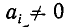
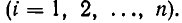
Для получения приближенных значений дробей используют частный вид цепных дробей, у которых все числители равны 1 
Форма записи (2), как и форма (1), очень громоздка; поэтому вместо (2) часто употребляются упрощенные записи, например
Все же часто мы будем пользоваться развернутой записью (2).
Ясно, что всякая цепная дробь вида (2) выражает некоторое рациональное число. Чтобы получить выражение этого числа в виде обыкновенной дроби, надо «свернуть» цепную дробь, выполняя (начиная «с конца») все указанные операции.
Пример:
Вычислить значение цепной дроби 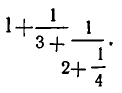
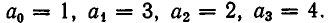
Ответ:
Обращение конечной цепной дроби в обыкновенную — всегда выполнимая задача. На это потребуется не более чем n шагов, каждый из которых состоит в сложении двух чисел: целого числа и правильной дроби.
Представление рациональных чисел в виде конечной цепной дроби
В предыдущем параграфе было показано, что любую конечную цепную дробь можно обратить в рациональное число. Покажем теперь, что и обратно — любое рациональное число r можно обратить в цепную дробь.
Теорема:
Всякое рациональное число можно представить в виде конечной цепной дроби.
Доказательство:
Всякое рациональное число r можно представить в виде отношения двух целых чисел 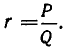

где 
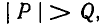
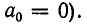
Нетрудно заметить, что каждое из этих равенств можно понимать как нахождение целой части неправильной дроби; каждое из неполных частных 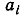
Подставив значение дроби 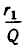
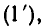
Затем значение дроби 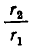
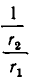
Число частных знаменателей, которое получится при разложении заданного рационального числа в цепную дробь, заранее узнать невозможно. Оно зависит от «природы» числа. Так, мало отличающиеся «на вид» числa 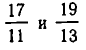
разлагаются в цепные Дроби, имеющие разное число частных знаменателей:
Обратите внимание на характер доказательства теоремы 1. По существу получено больше, чем требовалось. Ведь надо было лишь доказать, что любое рациональное число можно представить в виде конечной цепной дроби. Мы же не только доказали этот факт, но и указали способ построения искомой цепной дроби.
Покажем теперь, что разложение любого рационального числа в цепную дробь однозначно определено. При этом рассматриваются лишь разложения, удовлетворяющие следующему условию: последний частный знаменатель должен быть больше 1. В противном случае могут существовать и различные разложения в цепную дробь одного и того же рационального числа.
Пример:
Разложим в цепную дробь число
Последний частный знаменатель можно представить в виде 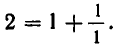
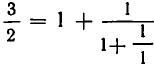
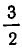
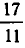
Чтобы исключить двузначность в разложении рационального числа в цепную дробь, связанную с такими искусственными «удлинениями», как раз и приходится предполагать последний частный знаменатель большим 1.
Однозначность разложения мы докажем от противного. Допустим, что число 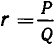
При этом допускается, что различны не только сами частные знаменатели, но и их количество 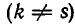
Мы имеем равенства:
Так как 
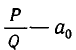
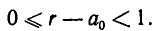
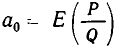
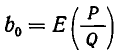
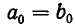
Отсюда следует, что
Но точно так же 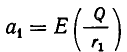
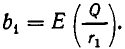
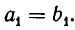
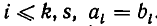
которое невозможно, поскольку 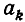
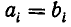
Подходящие дроби
Как уже говорилось, цепные дроби служат для получения приближенных значений, имеющих малые знаменатели. Эти приближенные значения получаются так: число разлагают в цепную дробь и обрывают процесс разложения на некотором шагу, заменяя смешанную дробь ее целой частью. Получающиеся таким образом дроби называются подходящими дробями для данной цепной дроби. Иными словами, подходящими дробями для заданной цепной дроби
У цепной дроби с n частными знаменателями имеется ровно n подходящих дробей; последняя подходящая дробь равна данной цепной дроби.
Пример:
Вычислим подходящие дроби цепной дроби [1, 2, 3, 4,]:
Чем больше номер подходящей дроби, тем утомительнее ее непосредственное обращение в обыкновенную дробь. При этом все предыдущие вычисления оказываются бесполезными для дальнейшего, все приходится выполнять вновь.
Естественно искать путь вычисления подходящих дробей данной цепной дроби, при котором использовались бы значения предыдущих дробей. Оказывается, для этого можно использовать так называемые рекуррентные соотношения между тремя последовательными подходящими дробями.
Вернемся к предыдущему примеру. Запишем подходящие дроби следующим образом:
Правило, по которому записаны третья и четвертая подходящие дроби, таково: в числителе записываются два слагаемых — числители двух предыдущих подходящих дробей, а в знаменателе — знаменатели предыдущих подходящих дробей, как показано ниже. И тут и там делается пропуск для множителя:
Оставленное место для множителя заполняется соответствующим частным знаменателем.
Докажем это правило в общем виде. Обозначим числитель и знаменатель i-й подходящей дроби через 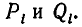
(здесь I = 2, 3, . . . , n).
Доказательство ведется с помощью математической индукции по индексу i.
Проверим сперва правило для i = 2; первые три подходящие дроби имеют вид:
Отсюда следует, что
Таким образом, правило верно при i = 2.
Допустим теперь, что правило верно для i = k — 1, то есть что
Докажем, что это же правило верно и при i=k, а именно, что имеет место равенство:
Чтобы получить k-ю подходящую дробь, надо в (k — 1)-й подходящей дроби (k — 1)-й частный знаменатель 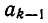
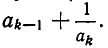
По предположению индукции имеем:
Итак, наша формула верна и при i=k. Значит, она верна при всех Иными словами, мы доказали, что
Для того чтобы формулы (3) и (4) не теряли смысла при i = 1, вводят определения 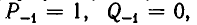
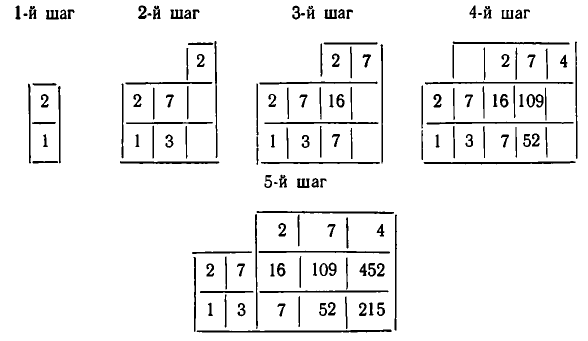
Покажем, как проводится вычисление, на примере цепной дроби [2, 3, 2, 7, 4]. Вычисление удобно располагать в табличку, которую заполняют последовательно. Первые два столбика заполняют компонентами первых двух подходящих дробей (нулевой и первой подходящей дроби), которые вычисляются непосредственно; третий столбик заполняется компонентами второй подходящей дроби, которые находятся по правилу: числитель первой подходящей дроби умножается на второй частный знаменатель, к полученному произведению прибавляется числитель нулевой подходящей дроби: так же находится и знаменатель второй подходящей дроби. Точно так же определяются числители и знаменатели последующих подходящих дробей. Вот последовательные шаги заполнения таблички:
Значит,
Свойства подходящих дробей
Полученное выше правило вычисления подходящих дробей имеет фундаментальное значение для всей теории цепных дробей. Кроме способа непосредственного вычисления последовательности подходящих дробей, из него получается ряд важных свойств частных числителей и частных знаменателей и подходящих дробей цепной дроби.
Рассмотрим некоторые из этих свойств.
1) Докажем, что для i =1, 2, 3, . . . , n имеет место равенство:
Доказательство проведем индукцией по индексу i.
Покажем прежде всего справедливость формулы (1) при i=1. Заметим, что 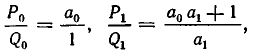
откуда следует, что
то есть формула (1) справедлива при i = 1.
Предположим, что формула (1) справедлива при i = m — 1:
Докажем, что она справедлива и при i = m, то есть что
Для этого выразим 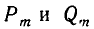
В силу формулы (1′) получаем:
Итак, из справедливости формулы (1) при i = m — 1 следует ее справедливость при i = m. Значит, она верна при всех значениях i.
2) Докажем, что при i = 1,2,3,… имеет место равенство:
Доказательство:
Преобразуем левую часть равенства (2) и применим свойство (1):
Из последних двух свойств вытекает важное следствие.
3) Пoдходящие дроби цепной дроби несократимы.
Будем доказывать это утверждение от противного. Предположим, что какая-то дробь 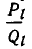
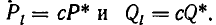
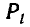
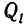
Но последнее равенство неверно, так как левая часть делится на с, а правая — нет. Следовательно, наше предположение, что частные числитель и знаменатель 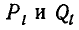
Диофантовы уравнения первой степени
Мы знаем, что одно уравнение с двумя неизвестными, вообще говоря, имеет бесчисленное множество решений. Однако если рассматривать такие уравнения лишь в множестве целых чисел, то может оказаться, что уравнение имеет лишь конечное множество решений.
Например, уравнение 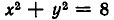
Уравнения, для которых ищутся лишь целые решения, обычно называют диофантовыми.
Вопрос о решении уравнений в целых числах довольно сложен. Мы рассмотрим сейчас самый простой вид таких уравнений, а именно уравнения вида
где а, b и с — целые числа.
Такие уравнения можно решать с помощью цепных дробей. Для примера рассмотрим
Разложим 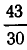
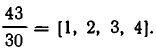
Умножим обе части равенства (2) на 11:
Получилось, что х = 77 и у = — 110 являются решениями заданного уравнения.
Нетрудно заметить, что решением того же уравнения будет любая пара чисел (х, у), следующим образом выражающихся через целый параметр t:
Этот метод всегда применим, если с делится на наибольший общий делитель чисел а и b. В противном случае уравнение не имеет целых решений.
Иногда ставится задача решений диофантовых уравнений в множестве натуральных чисел. Для этого нужно сначала решить его в целых числах, а потом найти значения t, при которых х и у положительны.
В разобранном выше примере для этого нужно решить в целых числах систему неравенств:
Решая ее, находим t = 3, 4, 5, . . .
Подходящие дроби и календарь
Астрономы подсчитали, что время полного оборота Земли вокруг Солнца приближенно равно 365 суткам 5 часам 48 минутам 46 секундам. Если это время выразить в сутках, то получим приближенно 365,2422 суток.
Обратим дробную часть в цепную дробь:
Первые три подходящие дроби:
Первая подходящая дробь 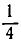
Однако через столетия снова начала накопляться ошибка. Чтобы ее оценить, рассмотрим разность
Таким образом, за каждые 132 года прибавляется лишний день (за 396 лет — 3 лишних дня).
Более точный календарь был введен папой Григорием XXII в 1582 году.
Во-первых, он выкинул в этом году 10 дней (следующий день после четверга 4 октября 1582 года именовался пятницей 15 октября), во-вторых, постановил в каждые четыреста лет три високосных года обращать в простые, а один оставить високосным. При переходе нашей страны на григорианский календарь в 1918 году разница во времени уже возросла до 13 суток, что и составляет разницу между старым и новым стилем.
Приближение цепной дроби подходящими дробями
Выясним теперь характер приближения подходящих дробей к рациональному числу, разложенному в данную цепную дробь. Для этого нам понадобится следующее утверждение.
Теорема:
Пусть дана цепная дробь длины т:
При увеличении последнего знаменателя 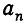
Доказательство:
Проведем доказательство с помощью индукции по n. При n = 0 утверждение очевидно. В этом случае «дробь» имеет вид 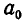
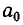
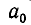
Пусть теорема уже доказана для дробей длины k. Рассмотрим дробь длины 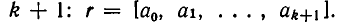
— цепная дробь длины k.
Пусть k + 1 — четное число. Тогда — дробь нечетной длины k. Поэтому по предположению индукции она уменьшается при увеличении 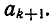
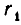
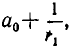
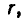
Если же k + 1 — нечетное число, то 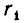
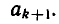
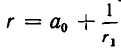
Итак, предположив, что теорема верна для n = k мы доказали ее справедливость при n = k + 1. Так как при n = 0 она верна, то она справедлива для всех значений n.
Из теоремы 2 вытекает важное
Следствие:
Всякая четная подходящая дробь не больше значения цепной дроби у а всякая нечетная подходящая дробь не меньше этого значения.
Доказательство:
Пусть дана дробь
— ее k-я подходящая дробь. Дробь r можно записать в виде
Таким образом, цепная дробь r получается из подходящей дроби 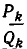
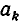
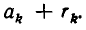
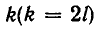
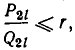
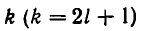
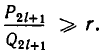
Из этого следствия вытекает, что если 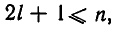
Более точную информацию о характере приближения подходящих дробей 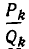
Теорема:
Имеют место неравенства
Доказательство:
Подходящая дробь 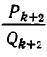
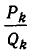
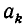
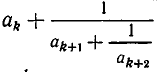
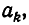
Из теоремы 3 и следствия из теоремы 2 вытекает, что четные подходящие дроби приближаются к числу 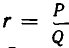
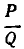
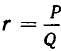
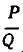
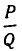
Знак равенства имеет место слева, если n = 2l, и справа, если n = 2l + 1.
Оценим теперь отклонение подходящей дроби 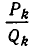
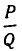
По формуле (1) из п. 6 имеем:
Из формул (1) и (2) следует, что
Так как
Видео:Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать

Бесконечные цепные дроби
Разложение иррациональных чисел в цепные дроби: До сих пор мы разлагали в цепные дроби рациональные числа. При этом процесс нахождения частных знаменателей сводился на каждом шагу к выделению целой части неправильной обыкновенной дроби.
Возьмем теперь какое-нибудь иррациональное число, например 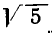
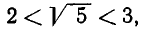
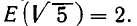
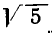
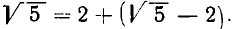
Таким образом,
Выделим целую часть числа 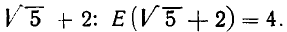
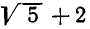
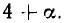
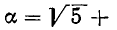
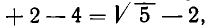
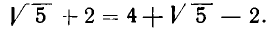
В итоге получилось:
Проделаем еще один аналогичный шаг:
Нетрудно заметить, что процесс выделения целой части и образования цепной дроби в данном примере не имеет конца. В каждом новом знаменателе будет появляться 4 и слагаемое 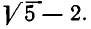
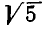
Мы видим, что цепные дроби являются хорошим аппаратом для вычисления квадратных корней.
Проверим, насколько полезен этот способ — как точно находится значение 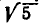
Для сравнения будем брать подходящие дроби и обращать их в обыкновенные, а затем полученные обыкновенные — в десятичные. Десятичные приближения, получаемые из подходящих дробей, будем сравнивать со значением 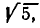
Получилось, что уже для четвертой подходящей дроби результат приближения 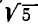
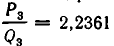
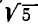
Возьмем произвольное иррациональное число а. Выделим его целую часть и обозначим ее через
где 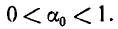
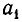
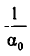
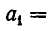
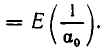
гдe
Пусть 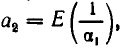
Через n шагов получим:
где 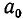

для которой 
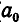
Построим для полученной дроби последовательность ее подходящих дробей (в отличие от случая разложения рациональных чисел эта последовательность бесконечна). Можно доказать, что последовательность
подходящих дробей сходится к разлагаемому числу а. Мы опускаем здесь это доказательство.
Подходящие дроби и наилучшие приближения иррациональных чисел рациональными
Мы научились изображать любые числа, как рациональные, так и иррациональные, в виде цепных дробей. Выясним теперь, в чем заключаются преимущества и недостатки такого изображения.
Основное преимущество записи чисел в виде цепных дробей по сравнению с их записью в виде систематических (например, десятичных) дробей состоит в том, что эта запись не зависит от выбора системы счисления. Ведь неполные знаменатели получались путем выделения целой части из неправильных дробей, а эта операция при любой системе счисления приводит к одному и тому же результату (конечно, с точностью до записи в разных системах счисления самих неполных знаменателей). Поэтому запись числа в виде цепной дроби отражает его «существенные» арифметические свойства, а не свойства, связанные с выбором той или иной системы счисления.
Например, при записи рационального числа в виде систематической дроби может получиться либо конечная дробь, либо бесконечная периодическая или смешанная) дробь. При записи же рационального числа в виде цепной дроби всегда получается конечная дробь, причем это характерно только для рациональных чисел. Можно доказать, что квадратичные иррациональности, и. только они, представляются в виде периодических цепных дробей. Выразить же условие того, что данное число является квадратичной иррациональностью, в терминах систематических дробей невозможно.
Но самое важное преимущество цепных дробей по сравнению с систематическими заключается в том, что они дают наилучшие приближения данного числа с помощью дробей, имеющих не слишком большие знаменатели. Уточним это утверждение.
Пусть даны число 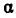
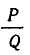
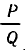
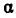
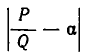
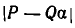
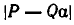
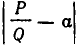
Пусть число 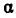
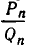
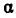
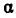
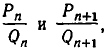
Оказывается, для любой дроби, знаменатель которой не превосходит 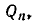
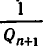
Теорема:
Если 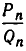
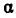
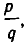
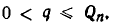
Единственным исключением является подходящая дробь 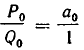
Доказательство этой теоремы мы опускаем.
Теорема 4 показывает, что подходящие дроби являются наилучшими приближениями для числа 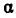
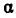
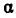
Отметим, что цепные дроби как аппарат для изображения действительных чисел имеют и недостатки: дело в том, что над действительными числа ми, изображенными в виде цепных дробей, практически трудно выполнять арифметические операции — сложение, вычитание, умножение и деление. (Попробуйте, например, сложить или перемножить дроби
[2, 1, 3, 1, 4] и [3, 2, 4, 6, 8 ],
не переводя их в обыкновенные.)
Цепные дроби как вычислительный инструмент
Рассмотрим некоторые примеры приближения иррациональных чисел подходящими дробями.
Начнем с числа 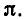
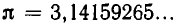
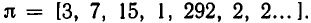
а затем составим таблицу для вычисления последующих дробей с помощью рекуррентного правила:
Получаем подходящие дроби 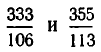
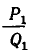
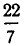
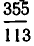
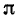
Чтобы оценить эту точность, используем формулу
В нашем случае
то есть точность полученного ответа превышает 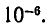
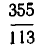
С помощью цепных дробей можно выполнять вычисление логарифмов при любом основании. Вычислим, например, 1g 20. Полученный результат будем сравнивать со значением 1g 20, взятым из таблицы Брадиса:
Обозначим искомое число через х; 1g 20 = х. Значит,
Ясно, что 1
Последнее равенство возведем в степень
Подставим значение 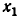
Отсюда 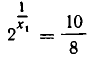
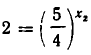
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🎬 Видео
Математика-947. Диофантовы уравнения и цепные дробиСкачать

Теория чисел. 6. Методы решения сравнений 1 й степениСкачать

Классический способ решения Диофантовых уравнений ➜ Решите уравнение в целых числах ➜ 13x-7y=6Скачать

Решение диофантовых уравненийСкачать

Решите уравнение в целых числах 3x^2+5y^2=345 ✱ Диофантовы уравнения ✱ Как решать?Скачать

Решите уравнение в целых числах 5x-4y=3 ➜ Как решать Диофантовы уравнения?Скачать

Дробно-рациональные уравнения. 8 класс.Скачать

Линейные диофантовы уравненияСкачать

Решение уравнений в целых числахСкачать

Методы решения диофановых уравненийСкачать

Как решать Диофантовы уравнения ➜ Решите уравнение в целых числах 4x+5y=6Скачать

ОКТЧ 6. Диофантовы приближения. Цепные дробиСкачать

ОКТЧ 22. Диофантовы приближения. Цепные дробиСкачать

Диофантовы уравнения x²+xy-y=2Скачать

Диофантовы уравнения x³-y³=91Скачать