4.10. Краевые задачи для ОДУ. Метод стрельбы
4.10.1. Граничные условия
Кроме задачи Коши, в которой дополнительные условия, накладываемые на решение ОДУ и его производные, задаются в одной точке , существует большое число задач с дифференциальными уравнениями, в которых дополнительные условия устанавливают связь между значениями функции и ее производных в нескольких точках отрезка, на котором разыскивается решение. Такие задачи называются многоточечными. В общем случае для дифференциального уравнения -го порядка на отрезке задается точек и соотношений вида
связывающих значения функции и ее производных до порядка n — 1 в этих точках.
При k = 2, x1 = a и x2 = b задача называется краевой или граничной. Такие задачи наиболее часто встречаются в приложениях. Для решения двухточечных краевых задач существует большое число методов, многие из которых основаны на сведении исходной задачи к решению ряда задач Коши.
4.10.2. Метод стрельбы для краевой задачи с ОДУ 2-го порядка
Рассмотрим краевую задачу
Рассмотрим также задачу Коши для уравнения (22) с начальными условиями
где — угол наклона касательной к интегральной кривой в точке . Считая решение задачи Коши (22),(24) зависящим от параметра , т.е. , надо найти такое значение параметра , при котором (т.е. при котором интегральная кривая попадет в точку с координатами ). Тогда решение задачи Коши совпадет с решением краевой задачи (22),(23). Условие попадания интегральной кривой в точку можно сформулировать в виде нелинейного уравнения относительно неизвестного :
Уравнение (25) отличается от обычных уравнений тем, что функцию нельзя представить аналитическим выражением, она выражается через решение задачи Коши (22),(24). Однако для решения (25) можно использовать рассмотренные ранее известные приближенные методы, в том числе простейший метод дихотомии.
Прежде всего надо определить исходный отрезок , на концах которого функция принимает значения разных знаков. Такой отрезок должен содержать в себе корень уравнения . Далее для снова решается задача Коши, определяется знак и в соответствии с этим выбирается новый отрезок — или — на котором функция меняет знак, и так далее до тех пор, пока разность двух последовательных приближений не станет меньше заданной величины . Название «метод стрельбы» связано с тем, что здесь как бы проводится «пристрелка» решения задачи Коши по углу наклона интегральной кривой в начальной точке отрезка. Этот алгоритм применим, если решение задачи Коши (22),(24) не слишком чувствительно к изменению .
Для решения задачи Коши (22),(24) можно использовать любой из рассмотренных ранее методов, записав задачу в виде системы уравнений 1-го порядка:
Другой вариант метода стрельбы можно получить, используя линеаризацию по Ньютону уравнения (25). Пусть — некоторое приближение к , тогда
и можно предложить следующий алгоритм последовательных приближений:
Производная может быть заменена в последнем выражении разностной производной . Такой вариант метода Ньютона называется методом секущих:
Видео:Методы решения нелинейных краевых задач для ОДУСкачать

Метод стрельбы
Рассмотрим краевую задачу для уравнения второго порядка, разрешенного относительно второй производной:

Будем искать решение Y = Y(x) этого уравнения на отрезке [0,1]. Любой отрезок [а, b]можно привести к этому отрезку с помощью замены переменной
Граничные условия на концах рассматриваемого отрезка примем в простейшем виде (1.37), т.е.

Сущность метода стрельбы заключается в сведении решения краевой задачи (1.41), (1.42) к решению последовательности задач Коши для того же уравнения (1.41) с начальными условиями

Здесь Y0 — точка на оси ординат, в которой помещается начало искомой интегральной кривой; α — угол наклона касательной к интегральной кривой в этой точке (рис. 1.5).
Рис. 1.5. Метод стрельбы
Считая решение задачи Коши 





Например, при использовании метода деления отрезка пополам поступаем следующим образом. Находим начальный отрезок 



Описанный алгоритм называется методом стрельбы вполне оправданно, поскольку в нем как бы проводится «пристрелка» по углу наклона интегральной кривой в начальной точке. Следует отметить, что этот алгоритм хорошо работает в том случае, если решение 
Для решения уравнения (1.44) используют и другие методы. В частности, одним из самых надежных является метод Ньютона. Его применение состоит в следующем. Пусть α0 — начальное приближение к α*. Построим итерационный процесс для нахождения последующих приближений αkс помощью формулы Ньютона (1.11):

С учетом того, что 

Производную в знаменателе этого выражения можно найти численно:

Здесь Δα — произвольное малое возмущение α.
Для вычисления правой части (1.46) нужно решить задачу Коши при 

Алгоритм решения краевой задачи методом стрельбы с применением пристрелки по методу Ньютона представлен на рис. 1.6. Нахождение решения задачи Коши Y(x,α) входит в данный алгоритм в качестве отдельного модуля с входным данным α. На выходе модуля получается решение Y(x, α) в виде значений yi (i=0,1. п)в точках xi = ih, где h = l/n.
Рис. 1.6. Алгоритм метода стрельбы
Методы стрельбы могут также использоваться для решения системы уравнений. В этом случае краевая задача (а не задача Коши) может возникнуть в силу того, что значения одной части искомых функций заданы при одном значении независимой переменной (например, при х = 0), а другой — при другом (например х = 1).
Тогда «пристрелка» проводится по неизвестным значениям искомых функций при х = 0 до тех пор, пока не будут удовлетворяться соответствующие граничные условия при х = 1.
Например, рассмотрим систему двух уравнений первого порядка:

Граничные условия заданы в виде

Процесс решения этой краевой задачи методом стрельбы состоит в следующем. Выбирается некоторое α, являющееся начальным приближением для Z(0). Решается задача Коши для системы (1.47) с начальными условиями Y(0) =Y0,Z(0) = α. В результате решения при х = 1 получается некоторое значение Z(1, α) ≠ Z1. Если разность между этими величинами невелика, то найденное решение задачи Коши принимается за искомое решение краевой задачи. В противном случае находится уточненное значение αи процесс повторяется.
Таким образом, метод стрельбы может быть также использован для решения как краевых задач для уравнений высших порядков, так и систем уравнений.
Видео:Разностные методы решения краевых задач для ОДУ 2 порядка. Разностная производная. Метод стрельбыСкачать

Краевые задачи
Для однозначного определения неизвестной функции ( u(x) ) уравнение (1) дополняется двумя граничными условиями на концах отрезка ( [0, l] ). Задаваться может функция ( u(x) ) (граничное условие первого рода), поток ( w(x) = −k(x) frac (x) ) (граничное условие второго рода) или же их линейная комбинация (граничное условие третьего рода): $$ begin tag u(0) = mu_1, quad u(l) = mu_2, end $$ $$ begin tag −k(0) frac (0) = mu_1, quad k(l) frac (l) = mu_2 end $$ $$ begin tag −k(0) frac (0) + sigma_1 u(0) = mu_1, quad k(l) frac (l) + sigma_2 u(l) = mu_2. end $$
Эллиптические уравнения второго порядка, прототипом которых является уравнение (1), используются при моделирование многих физико-механических процессов.
Кроме того,могут рассматриваться задачи с несамосопряженным оператором, когда, например, $$ begin tag — frac left( k(x) frac right) + v(x) frac + q(x) u = f(x), quad 0 —>
💡 Видео
7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Лукьяненко Д. В. - Численные методы - Лекция 17Скачать

Метод ЭйлераСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Практика 1 ИзоклиныСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Дифференциальные уравнения. Задача Коши. Метод Эйлера.Скачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

2.1 Точные методы решения СЛАУ (Крамера, Гаусса, Жордана, прогонки)Скачать
Видеоурок "Системы дифференциальных уравнений"Скачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

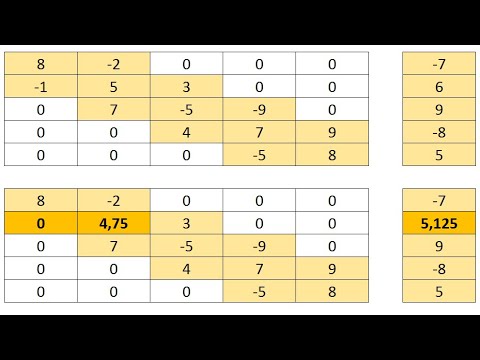
6-5. Алгоритм прогонкиСкачать

9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Частное решение дифференциального уравнения. 11 класс.Скачать



