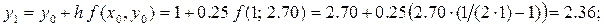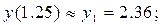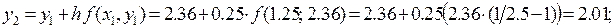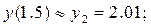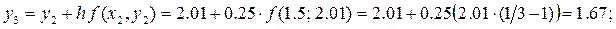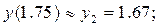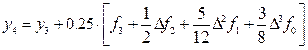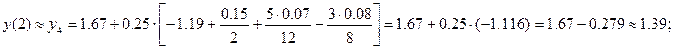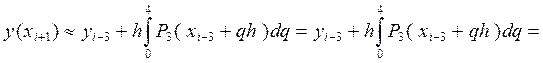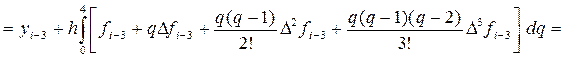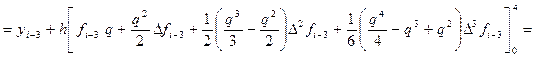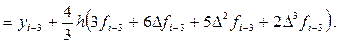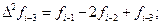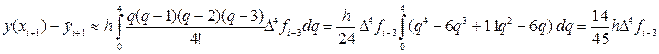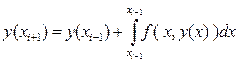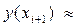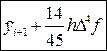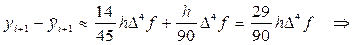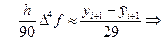Метод адамса решения дифференциальных уравнений пример решения

Видео:Решение обыкновенных дифференциальных уравнений. Часть 1Скачать

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ. Пример. Решить экстраполяционным методом Адамса уравнение:

Пример. Решить экстраполяционным методом Адамса уравнение:

(33)

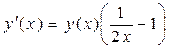
с начальным условием y(1) = 2.70 на интервале [1; 2.25], принимая h = 0.25 . В качестве разгонных точек x₀, x₁, x₂, x₃ и соответствующих решений y₀, y₁, y₂, y₃ для реализации метода Адамса взять значения, полученные методом Эйлера в точках: x₁, x₂, x₃. Все вычисления вести с тремя верными в узком смысле знаками.

Решение. Вычислительная схема экстраполяционного метода Адамса определяется выражением:

(10)

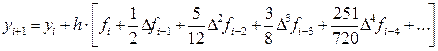
Поскольку на основе разгонных данных для функции f (x_i, y_i) можно вычислить только конечные разности до третьего порядка включительно: Df_i; D 2 f_i; D 3 f_i, то для решения данной задачи формула (10) перепишется в виде:

Далее в соответствии с условием задачи по методу Эйлера на интервале
[1; 1.75] с шагом h = 0.25 необходимо найти приближённые значения решения y₁, y₂, y₃ данного уравнения. Для этого используется численная схема, определяемая уравнением:

, i = 0, 1, …, n

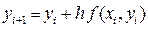
Очевидно, что для получения необходимых разгонных данных метода Адамса: y₁ » y(1.25); y₂ » y(1.5); y₃ » y(1.75) по методу Эйлера необходимо реализовать трёхшаговый вычислительный процесс.

Шаг 1:

В результате находим:

Шаг 2:

В результате находим:

Шаг 3:

В результате находим:

Таким образом, в качестве разгонных значений для метода Адамса имеем следующие приближённые значения решения:

Далее в соответствии с требованиями метода Адамса на основе полученных расходных данных вычислим приближённые значения функции:

f (x_i, y_i) = 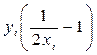i = 0, 1, 2, 3;

Далее для реализации метода Адамса на основе имеющихся данных составим для функции f (x_i, y_i) таблицу конечных разностей:

Теперь по формуле 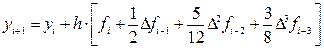при h = 0.25 и i = 3

получим:

и подставляя из таблицы 2 соответствующие значения функции f (x₃, y₃) = f₃ = — 1.19 и её конечных разностей: Df₂ = 0.15; D 2 f₁ = 0.07; D 3 f₀ = — 0.08; (которые в таблице 2 подчёркнуты) окончательно получим:

Далее на основе полученного приближённого значения y₄ = 1.39; вычисляем значение f (x₄, y₄) = f(2.00; 1.39) = f₄ = — 1.04; и конечные разности Df₃ = 0.15; D 2 f₂ = 0.00;
D 3 f₁ = — 0.07; (которые в таблице 2 обведены рамкой) окончательно получим при i = 4:

;

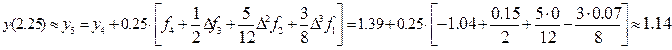
Этот вычислительный пошаговый процесс можно продолжать и далее…

Отметим, что для получения более точных результатов разгонные значения для метода Адамса целесообразно было бы получить более точным методом, например, методом Рунге-Кутта четвёртого порядка. Здесь мы использовали метод Эйлера исключительно из-за его просты.

§5. Метод Милначетвёртого порядка.

Ещё одним методом прогноза и коррекции, используемым на практике, является метод Милна, в рамках которого имеется две формулы – первая и вторая формулы Милна, которые используются соответственно для предсказания и уточнения (коррекции) искомого решения y(x) задачи Коши.

5.1 Первая формула Милна – формула предсказания.

Снова строим численный методы решения начальной задачи.

(34)

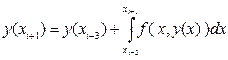
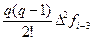
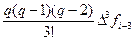
P₃(x _i—3 + qh) = f _i—3+ qD f _i—3 + + . (35)

При подстановке в выражение (34) полинома (35), зависящего от переменной 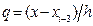, в интеграле формулы (34) необходимо сделать замену переменной:
x ® x _i—3 + qh; в соответствии с которой:

.

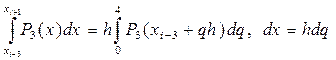
Поэтому в результате выражение (34) перепишется в следующем виде:

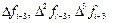
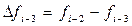
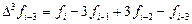
Отсюда, выразив конечные разности через значения функции f (x, y):

;

,

получим первую явную формулу (предсказания) Милна четвёртого порядка:

, (36)

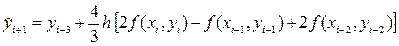
которая, очевидно, является экстраполяционной, поскольку делает предсказание решения y (x_i+1) на основе интерполяционного полинома, построенного по узлам
x_i–3, x _i–2, x_i–1, x_i. Далее в лекции, полученные по формуле предсказания (36) приближённые значения y_i для искомого решения y(x _i), будем обозначать как .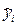

Оценка шаговой погрешности первой формулы Милна.

Главный член локальной погрешности формулы (36) можно найти при интегрировании первого из неучтённых в (35) слагаемого интерполяционного полинома Ньютона:

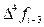
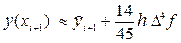
Считая значения четвёртых разностей примерно одинаковым в используемой области таблицы конечных разностей функции f_i, опустим индекс у функции f в записи ; в результате получим следующее приближённое представление решения в точке x _i+1 на основе первой формулы Милна:

(37)

5.2 Вторая формула Милна – формула уточнения.

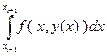
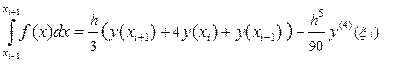
и применим к интегралу простейшую формулу Симпсона:

, где x_iÎ(x_i-1, x_i+1).

В результате получим:

(38)

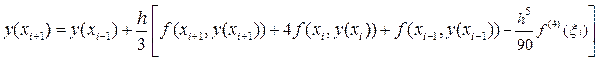
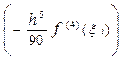
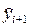
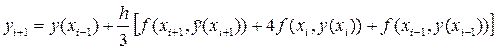
Отбрасывая в формуле (38) слагаемое , характеризующее ошибку квадратурной формулы Симпсона и заменяя значения решения y(x _i—1) и y(x _i) известными приближёнными значениями y _i—1 и y _i, а стоящее в правой части (38) в качестве аргумента функции f(x _i+1, y(x _i+1)) значение y(x_i+1) значением , полученным по первой (явной) формуле Милна (36), приходим ко второй интерполяционной (и неявной) формуле Милна – формуле уточнения.

(39)

Оценка шаговой погрешности второй формулы Милна.

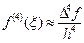
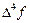
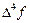
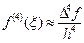
Для вывода приближённой оценки шаговой погрешности метода Милна воспользуемся приближённым равенством, связывающим производные и конечные разности , где так же, как и в (37), — условная запись практически постоянных четвёртых разностей. Иногда в качестве величины в формуле берут максимальную четвёртую разность из четвёртых конечных разностей в используемой части таблицы конечных разностей.

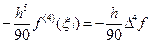
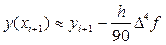
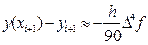
Исходя из точного равенства (38), локальную погрешность получаемого с помощью формулы (39) приближённого значения y_i+1 можно приближённо охарактеризовать величиной . Поэтому, сравнивая выражения (38) и (39), можем написать:

или (40)

Далее приравнивая правые части выражений (37) и (40):

» и

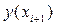
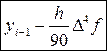
получим:

(41)

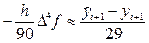
Следовательно, сравнивая выражения (40) и (41), окончательно получаем:

(42)

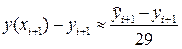
Таким образом, при численном интегрировании начальной задачи (1), (2) методом Милна четвёртого порядка, определяемым формулами (36), (39), на каждом i — м шаге следует вычислять величину

(43)

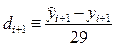
и сравнивать её модуль с величиной e > 0 допустимой шаговой погрешности. Если
½d_i+1½ _i+1) — y М _i+1 = 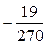(y М _i+1 — y Б _i+1). (33)

для предиктор-корректорного метода Адамса четвёртого порядка

(28)

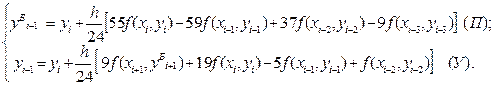
это характеризует метод Милна как несколько более точный при одинаковых вычислительных затратах.

§6. Сведение задачи Коши для систем дифференциальных уравнений первого порядка к задаче Коши для ОДУ первого порядка с использованием векторных обозначений.

Пусть имеется система дифференциальных уравнений первого порядка, разрешённых относительно производных. Задача Коши для такой системы дифференциальных уравнений формулируется в следующем виде:

(45)

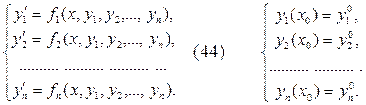
Введём следующие векторныеобозначения:

(46)

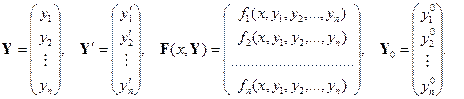
Используя введённые векторные обозначения (46) задача Коши (44), (45) для системы дифференциальных уравнений первого порядка (44) может быть переписана в виде:

, (47)

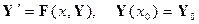
который имеет точно такую же форму, как и рассматриваемая выше задача Коши:

К полученному векторному дифференциальному уравнению (47) применимы все численные методы, изучавшиеся в рамках данной темы, поскольку все рассмотренные методы имеют линейную структуру (т.е. если реализацию какого-либо из рассмотренных методов решения задач Коши представить как действие соответствующего линейного оператора).

При таком подходе скалярными величинами в формулах, определяющих методы, являются только независимая переменная x и расчётный шаг h; всем остальным величинам соответствуют введённые выше векторные величины размерности n.

Следует лишь учесть, что в этом случае при контроле пошаговой или глобальной точности методов вместо модуля нужно использовать норму вектора (например, норму — максимум).

Заключение (план — аннотация лекции №24).

В лекции 24 рассмотрены приближённые методы решения задачи Коши, основанные на интегрировании ДУ и последующей замене подынтегральной функции интерполирующим полиномом соответствующего порядка, данные методы известные в литературе под общим названием многошаговых методов Адамса.

Дан вывод формул экстраполяционного метода Адамса, рассмотрен подход к оценке его точности. Приведён интерполяционный метод Адамса, рассмотрены его частные случаи. Рассмотрены предиктор-корректорные методы Адамса, дан метод осуществления пошагового контроля погрешности вычислений при их применении.

Ещё одним методом прогноза и коррекции, рассмотренным в лекции, является метод Милна, в рамках которого получены две формулы – первая и вторая формулы Милна, которые используются соответственно для предсказания и уточнения (коррекции) искомого решения y(x) задачи Коши. Обсуждается роль первой и второй формулы Милна в процессе формирования решения задачи Коши для ОДУ. Дана оценка шаговой (локальной) погрешности метода Милна.

Сформулирована задача Коши для системы ОДУ первого порядка и дифференциального уравнения второго порядка. Дана схема сведение задачи Коши для систем дифференциальных уравнений первого порядка к виду задачи Коши для обыкновенного дифференциального уравнения первого порядка.

Приведены примеры решения типовых задач.

1. В.М. Вержбицкий. Основы численных методов. – М.: Высшая школа, 2002. – 840 стр.

2. Мастяева И.Н., Семенихина О.Н. Численные методы: Учебное пособие / Московский международный институт эконометрики, информатики, финансов и права. – М.: МЭСИ М., 2003. – 102 стр.

3. Приклонский В.И. Численные методы. Лекционный курс, читаемый в МГУ. Адрес в Интернете ttp://afrodita.phys.msu.ru/download/priklonsky/lections/

Вопросы по теме

«Методы решения начальных задач для обыкновенных дифференциальных уравнений».

1. Основные определения и постановка задачи Коши для ОДУ: Определение ОДУ; уравнение, разрешённое относительно производной; начальная задача; начальные условия; геометрическая интерпретация задачи Коши; Классификация приближенных методов. Теорема об эквивалентности задачи Коши соответствующему интегральному уравнению. Метод последовательных приближений Пикара, его основные свойства.

2. Метод Эйлера. Общая характеристика метода Эйлера в классе численных методов решения задачи Коши. Геометрическая интерпретация метода Эйлера — метод ломаных. Квадратурный подход к выводу метода Эйлера. Модификации метода Эйлера (неявный или обратный метод Эйлера, метод трапеций, Метод Хьюна). Исправленный метод Эйлера, его достоинства и недостатки.

3. Методы решения задачи Коши с помощью формулы Тейлора.Исправленный метод Эйлера, его достоинства и недостатки. Методы Рунге-Куттакак способ модификации исправленного метода Эйлера.Вывод формул семейства методов Рунге-Кутта первого и второго порядка. Геометрическая интерпретация метода Рунге-Кутта второго порядка. Формулы для семейства методов Рунге-Кутта четвёртого порядка. Рекомендации по использованию методов Рунге-Кутта. Свойства сходимости и точности методов Рунге-Кутта.

4. Многошаговые методы Адамса.Экстраполяционный метод Адамса, подходы к оценке его точности. Интерполяционный метод Адамса и его частные случаи. Предиктор-корректорные методы Адамса, осуществление пошагового контроля погрешности вычислений при их применении.

5. Метод Милна. Первая и вторая формула Милна, их роль в процессе формирования решения задачи Коши для ОДУ. Оценка шаговой (локальной) погрешности метода Милна.

6. Разностные аппроксимации задачи Коши. Разностный способ решения задачи Коши. Разностные схемы на основе аппроксимации первой производной. Понятие устойчивости вычислительного процесса и сходимости разностной схемы. Локальные и глобальные ошибки вычислительных процессов решения начальных задач для ОДУ. Связь локальной и глобальной ошибки. Оценка глобальной ошибки численной схемы решения задачи Коши для ОДУ на основе метода Эйлера.

7. Задача Коши для системы ОДУ первого порядка и дифференциальных уравнений высших порядков. Сведение задачи Коши для систем дифференциальных уравнений первого порядка к виду задачи Коши для обыкновенного дифференциального уравнения первого порядка. Сведение дифференциальных уравнений высших порядков к соответствующим задачам Коши для систем дифференциальных уравнений первого порядка.

Дата добавления: 2015-09-14 ; просмотров: 10284 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Численные методы. Метод Адамса.Скачать

6.6. Интерполяционные методы Адамса

При S = 1 формула (6.16) примет вид

(6.22)

Если Q = 2, получим следующее вычислительное правило:

(6.23)

Обычно на практике используют экстраполяционную формулу (6.18), а затем корректируют полученное значение по формуле (6.23). И если результат уточненного значения не превышает допустимую погрешность расчета, то шаг H считается допустимым .

Для расчетов на компьютере формулы (6.18) и (6.23) в конечно-разностном виде неудобны. С учетом (6.21) их можно представить в виде

(6.24)

Приведенные формулы имеют достаточно большую точность. Они дают погрешность порядка

О( H4 ), но сами формулы оценки погрешности достаточно сложны. Приближенно погрешность можно оценить по правилу Рунге.

Пример 6.2. Решить дифференциальное уравнение на отрезке [0, 1] c начальным условием Y(X=0) = 1. Найти решение методом Адамса (с коррекцией) в точке X4, решение в трех первых точках найти методом Рунге- Кутта, приняв шаг .

Решение. Значения функции в четырех первых точках возьмем из табл. 6.1 (см. пример в предыдущем разделе). Теперь стало понятно, зачем мы сохраняли значения первой производной в этих точках (см. формулы (6.24)).

Для того чтобы скорректировать полученный результат, необходимо вычислить значение производной в этой точке:

Теперь уточним значение по интерполяционной формуле (а можно этого и не делать, тогда погрешность метода будет больше):

Так как в качестве нового значения функции принято скорректированное, то Обязательно Следует пересчитать значение производной. В нашем случае модуль разности экстраполяционной и интерполяционной формул меньше ε, Что позволяет продолжить вычисления с тем же шагом.

Вопросы для самопроверки

· Сформулируйте задачу Коши для обыкновенных дифференциальных уравнений первого порядка.

· Что является решением дифференциального уравнения: а) в высшей математике, б) в прикладной математике?

· Какие методы решения дифференциальных уравнений называются одношаговыми, многошаговыми? Приведите примеры.

· Сравните решения, полученные на первом, втором шаге методами Эйлера, Рунге-Кутта и разложением в ряд Тейлора (трудоемкость, погрешность…).

· Как оценить погрешность применяемого метода? Как ее уменьшить?

· Сравните одношаговые и многошаговые методы решения дифференциальных уравнений, указав достоинства и недостатки первых и вторых.

· Что такое экстраполяционные и интерполяционные методы (формулы) Адамса?

· Можно ли применять: а) только экстраполяционные методы Адамса,
б) только интерполяционные?

· Можно ли использовать: а) многошаговые методы без одношаговых;
б) одношаговые методы без многошаговых?

· При решении дифференциального уравнения методом Адамса на 27-м шаге необходимо сменить шаг. Как это сделать?

Видео:3_05. Многошаговые алгоритмы решения ОДУСкачать

Лабораторная работа по выч. математике №4 «Решение обыкновенных дифференциальных уравнений. Метод Адамса»

CАНКТ-ПЕТЕРБУРГСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ

Лабораторная работа по выч. математике №4

«Решение обыкновенных дифференциальных уравнений.

Выполнил: Припадчев Артём

Задание: составить подпрограмму для решения ОДУ первого порядка используя многошаговый метод Адамса. Разгонные точки вычислить методом Рунге-Кутта 4-го порядка. Вычисление правых частей реализовать отдельной подпрограммой. Найти решение заданного уравнения с точностью e, контролируя точность на каждом шаге вычислений, построить график решения.

Воспользовавшись хорошо зарекомендовавшей себя формулой Симпсона, можно получить еще более точную формулу для решения задачи Коши для ОДУ первого порядка — широко используемого в вычислительной практике метода Рунге-Кутты.

В формуле Симпсона для приближенного вычисления определенного интеграла используются значения подинтегрального выражения в трех точках. В интеграле их всего две, поэтому введем дополнительную точку в середине отрезка [xi+1 xi]

тогда можно переписать так:

Полученное выражение является неявным, так как в правой части содержатся еще не определенные значения функции yi+h/2 и yi+1. Чтобы воспользоваться этой формулой, надо использовать некоторое приближение для вычисления этих значений

При использовании различных методов приближенного вычисления этих величин, получаются выражения для методов Рунге-Кутты различного порядка точности.

Алгоритм Рунге-Кутты третьего порядка — РК3 (погрешность порядка h3):

(6.8)

Алгоритм Рунге-Кутты четвертого порядка — РК4 (погрешность порядка h4):

(6.9)

Алгоритмы третьего и четвертого порядков требуют на каждом шаге трех и четырех вычислений функции соответственно, но являются весьма точными.

Рассмотренный ранее метод Рунге-Кутты использует значение функции на одном предшествующем шаге, поэтому они относятся к так называемым одношаговым методам. Точность вычислений можно увеличить, если использовать при нахождении решения в некотором узле xi информацию о значениях функции, полученных в нескольких (k) предыдущих узлах сетки интегрирования (xi-1, xi-2 … xi-k).

Если используются значения в k предыдущих узлах, то говорят о k-шаговом методе интегрирования уравнения. Одним из способов построения многошаговых методов заключается в следующем. По значениям функции, вычисленным в k предшествующих узлах, строится интерполяционный полином степени (k-1) — , который используется при интегрировании дифференциального уравнения по выражению (6.3). Интеграл при этом выражается через квадратурную формулу:

,

где лl – квадратурные коэффициенты.

Очевидно, что при k=1 в качестве частного случая получается формула Эйлера. Значения квадратурных коэффициентов для k от 2 до 4 приведены в таблице.

📺 Видео

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

7.4 Многошаговые методыСкачать

Дифференциальные уравнения. Задача Коши. Метод Эйлера.Скачать

08 Методы АдамсаСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Пример 65. Решить задачу Коши (диффуры)Скачать

3_11. Алгоритм Рунге-КуттыСкачать

Дифференциальные уравнения. 11 класс.Скачать

Численное решение задачи Коши методом ЭйлераСкачать

Частное решение дифференциального уравнения. 11 класс.Скачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать