Решите уравнение 1 81 cosx 9 2sin2x на отрезке (3 видео)

Решите уравнение 1 81 cosx 9 2sin2x на отрезке

Вопрос по математике:

А) решите уравнение 1/81^ (cosx)= 9^( 2sin2x)
Б)найдите все корни принадлежащие отрезку (-3П;-2П)

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Содержание

Как написать хороший ответ?
Задача 16232 (1/81)^(cosx) = 9^(sqrt(2)sin2x), [-2Pi;.
Условие
Решение
Задание 13. Математика ЕГЭ. Решите уравнение
🎥 Видео

Ответы и объяснения 1

Вот решение. там справа число не видно это -5П/2

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Видео:Решите уравнение ➜ sin⁡x+cos⁡x=1 ➜ 2 способа решенияСкачать

Задача 16232 (1/81)^(cosx) = 9^(sqrt(2)sin2x), [-2Pi;.

Условие

(1/81)^(cosx) = 9^(sqrt(2)sin2x), [-2Pi; -Pi/2]

Решение

(1/81)^(cosx) = (9)^(sqrt(2)*sin2x)
(9^(-2)) ^(cosx) = (9^(sqrt(2)*sin2x)
(9) ^(-2cosx) =9^(-2sqrt(2)sin2x)
-2cosx=-2sqrt(2)sin2x;
-2cosx+2sqrt(2)sinx*cosx=0
2cosx*(sqrt(2)*sinx-1)=0
cosx=0 или sinx=1/sqrt(2)
x=(π/2)+πk, k∈Z или х= (π/4)+2πm, m∈Z или х= (3π/4)+2πn, n∈Z

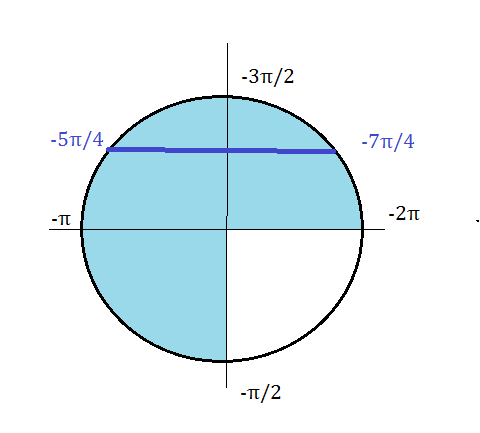
б) Указанному промежутку принадлежат корни

О т в е т.
а) (π/2)+πk, (π/4)+2πm, (3π/4)+2πn, k, m, n∈Z

б) Указанному промежутку принадлежат корни
(-7π/4);(-3π/2);(-5π/4); (-π/2)

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Задание 13. Математика ЕГЭ. Решите уравнение

Задание.

а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку [ — 2π; — π/2].

Решение:

а) Решите уравнение

ОДЗ уравнения — все числа.

Преобразуем данное уравнение, представим степень в левой части уравнения в виде степени с основанием 9, для этого:

(9 -2 ) cosx = 9 2sin2x

9 -2cosx = 9 2sin2x

Получившееся показательное уравнение равносильно уравнению

2sin2x + 2cosx = 0

Воспользуемся формулой двойного аргумента: sin2x = 2·sinx·cosx

2·(2·sinx·cosx + 2cosx) = 0

4sinx·cosx + 2cosx = 0

2cosx(2sinx + 1) = 0

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом не теряет смысла, следовательно, получаем:

2cosx = 0 или 2sinx + 1 = 0

1) Решим уравнение 2cosx = 0

2)Решим уравнение 2sinx + 1 = 0

б) Укажите корни этого уравнения, принадлежащие отрезку [ — 2π; — π/2].