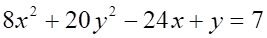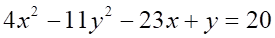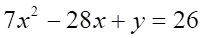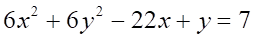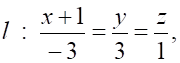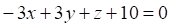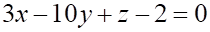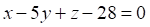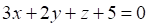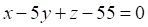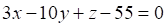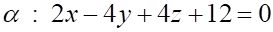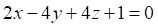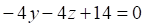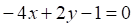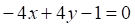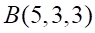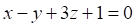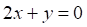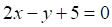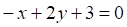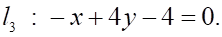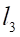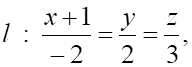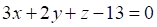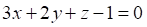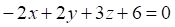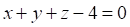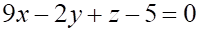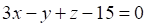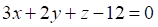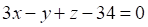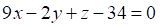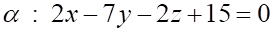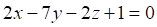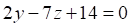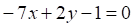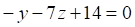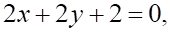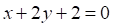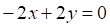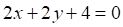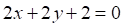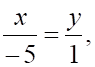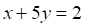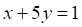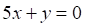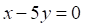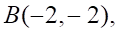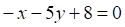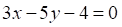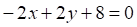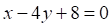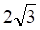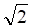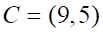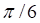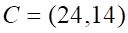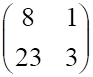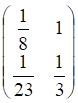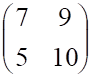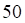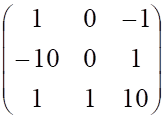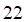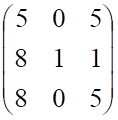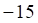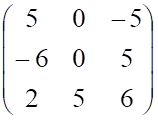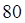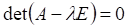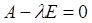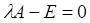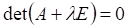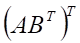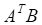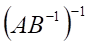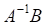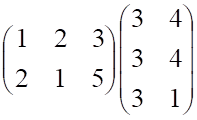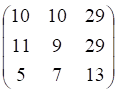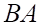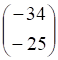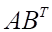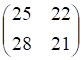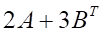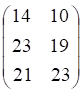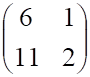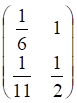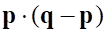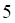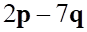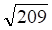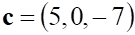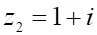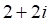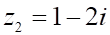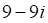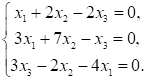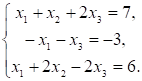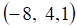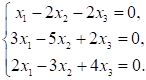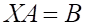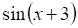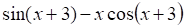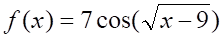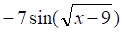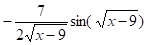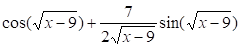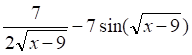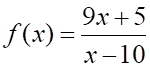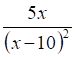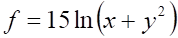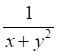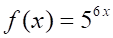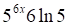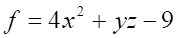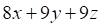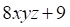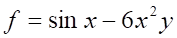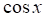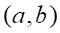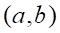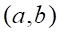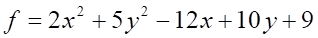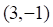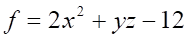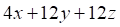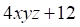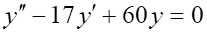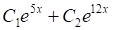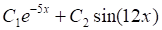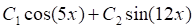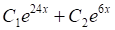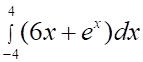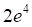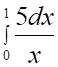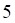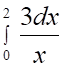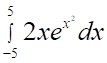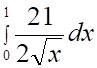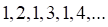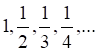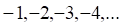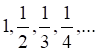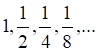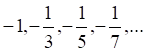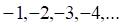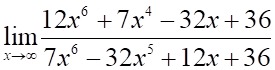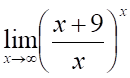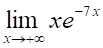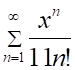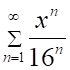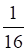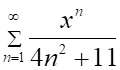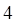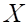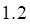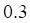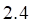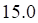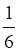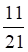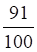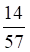Матричное уравнение ax b с невырожденной квадратной матрицей а имеет

Видео:Лекция 8. Решение матричных уравненийСкачать

Матричное уравнение ax b с невырожденной квадратной матрицей а имеет

Решить матричное уравнение.

Записываем в матричном виде AX=B

Равенство AX=B обычно называют матричным уравнением, и если матрица А невырожденная, то можно найти решение уравнения AX=B с помощью обратной матрицы А -1

Пусть | А | 0. Умножая обе части AX=B на А -1 слева, получим А -1 (AX) = А -1 B ,

откуда A -1 (AX) = (A -1 A) X = EX = А -1 B

Последнее равенство даёт нам все решения матричного уравнения

det | А | = 4 (11) + 3 (4) + 18 (-3) = 44 + 12 — 54 = 56 — 54 = 2

Вычислим алгебраические дополнения элементов матрицы А:

Видео:§28 Матричные уравненияСкачать

Решение матричных уравнений: теория и примеры

Видео:Решение матричных уравненийСкачать

Решение матричных уравнений: как это делается

Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,

где x — неизвестное.

А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.

Итак, матричным уравнением называется уравнение вида

где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.

Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу слева:

.

По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому

.

Так как E — единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :

.

Как решить матричное уравнение во втором случае? Если дано уравнение

то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:

,

,

.

Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X . То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A .

Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения

.

Видео:2 13 Решение матричного уравнения AXB=CСкачать

Решение матричных уравнений: примеры

Пример 1. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

.

Найдём алгебраические дополнения матрицы A :

.

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

.

Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :

.

Наконец, находим неизвестную матрицу:

Пример 2. Решить матричное уравнение

.

Пример 3. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

.

Найдём алгебраические дополнения матрицы A :

.

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

.

Находим матрицу, обратную матрице A :

.

Находим неизвестную матрицу:

До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.

Пример 4. Решить матричное уравнение

.

Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

.

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

.

Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:

.

Находим неизвестную матрицу:

Пример 5. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

.

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

.

Находим матрицу, обратную матрице A :

.

Находим неизвестную матрицу:

Пример 6. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

.

Найдём алгебраические дополнения матрицы A :

.

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

.

Находим матрицу, обратную матрице A :

.

Найдём матрицу, обратную матрице B .

Сначала найдём определитель матрицы B :

.

Найдём алгебраические дополнения матрицы B :

Составим матрицу алгебраических дополнений матрицы B :

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B :

.

Находим матрицу, обратную матрице B :

.

Видео:Обратная матрицаСкачать

Тест Комплексный с ответами по Высшей математике (Кривой II порядка …)

Видео:Матричное уравнениеСкачать

Тесты по высшей математике с ответами

Видео:Матричные уравнения Полный разбор трех типов матричных уравненийСкачать

Комплексный сборник тестов с ответами по Высшей математике (Кривой II порядка является …)

Видео:Матричный метод решения систем уравненийСкачать

Кривые второго порядка

1. Кривой II порядка является

— эллипс, не вырожденный в окружность +

2. Кривой II порядка является

— эллипс, не вырожденный в окружность

3. Кривой II порядка является

— эллипс, не вырожденный в окружность

4. Кривой II порядка является

— эллипс, не вырожденный в окружность

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Прямые и плоскости в пространстве

Правильный ответ выделен

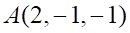
1. Уравнением плоскости, проходящей через точку и перпендикулярной прямой является

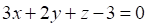
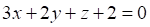
а. б. в.

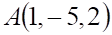
2. Общее уравнение плоскости, содержащей точку и параллельной плоскости , имеет вид

г.

3. Плоскость перпендикулярна плоскости

б.

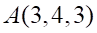
4. Прямая, проходящая через точки и , перпендикулярна плоскости

в.

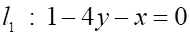
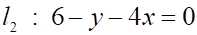
5. Даны три прямых на плоскости: , и Верным является утверждение

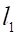
а. и перпендикулярны

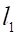
б. и перпендикулярны

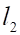
в. и перпендикулярны

г. перпендикулярных прямых нет

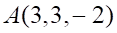
6. Уравнением плоскости, проходящей через точку и перпендикулярной прямой является

в.

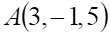
тест 7. Общее уравнение плоскости, содержащей точку и параллельной плоскости , имеет вид

г.

8. Плоскость перпендикулярна плоскости

б.

Видео:Решить матричное уравнениеСкачать

Прямые на плоскости

Правильный ответ выделен.

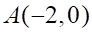
1. Прямая, проходящая через точку и параллельная прямой имеет вид

в.

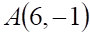
2. Уравнением прямой, содержащей точку и параллельной прямой является

б.

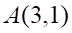
3. Общее уравнение прямой, содержащей точки и имеет вид

б.

Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Треугольник на плоскости

Правильный ответ выделен

1. Длина стороны AB в треугольнике с вершинами ABC , равна

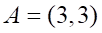
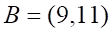
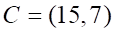
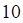
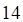
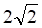
а. б. в. г.

2. Длина медианы AM в треугольнике с вершинами ABC , равна

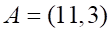
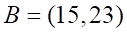
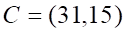
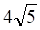
а. б. в. г.

3. Угол ABC в треугольнике с вершинами

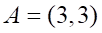
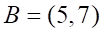
а. прямой б. тупой в. острый

4. В треугольнике ABC, где …, угол при вершине A равен

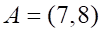
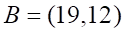
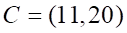
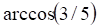
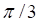
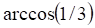
а. б. в. г.

5. В треугольнике ABC, угол ABC

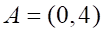
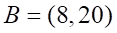
а. прямой б. тупой в. острый

Видео:§29 Решение матричного уравненияСкачать

Линейная алгебра. Алгебра матриц. Обратная матрица. Определители

Правильный ответ выделен

1тест. Обратной к данной матрице является матрица

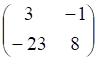
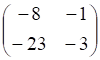
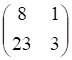
а. б. в. г.

2. Определитель данной матрицы равен

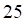
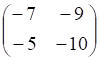
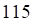
а. б. в. г.

3. Определитель данной матрицы равен

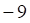
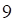
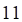
а. б. в. г.

4. Определитель данной матрицы равен

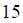
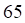
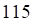
а. б. в. г.

5. Определитель данной матрицы равен

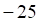
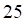
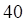
а. б. в. г.

6. Уравнение для нахождения собственных значений матрицы A имеет вид

а.

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Сумма и произведение матриц

Правильный ответ выделен.

1. Выражение, показанное выше, эквивалентно

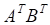
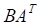
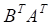
а. б. в. г.

2. Выражение , показанное выше, эквивалентно

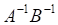
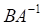
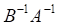
а. б. в. г.

3. Произведение , показанное выше, матриц равно

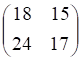
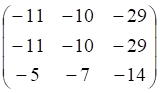
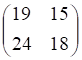
а. б. в. г.

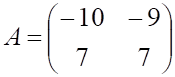
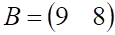
4. Заданы матрицы , показанные выше, и . Произведение ВА равно

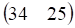
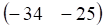
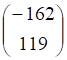
а. б. в. г.

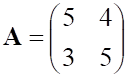
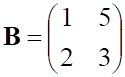
5. Заданы , показанное выше, матрицы. Произведение , показанное выше, равно

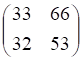
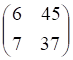
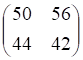
а. б. в. г.

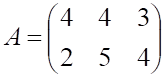
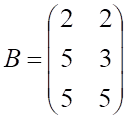
6. Заданы , показанное выше, матрицы и . Сумма , показанное выше, равна

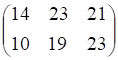
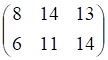
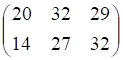
а. б. в. г.

тест №7. Транспонированной к , показанное выше, матрице является матрица

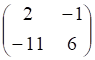
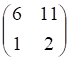
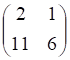
а. б. в. г.

Видео:Матричное уравнение. Пример 1Скачать

Векторная алгебра

Правильный ответ выделен.

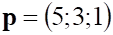
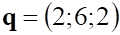
1. Заданы, показанное выше, векторы. Выражение, показанное выше, равно

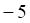
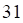
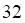
а. б. в. г.

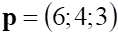
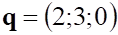
2. Заданы , показанное выше, векторы . Длина , показанное выше, вектора равна

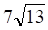
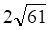
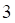
а. б. в. г.

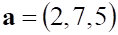
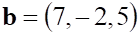
3. Из , показанное выше, векторов , ортогональными являются

Видео:Обратная матрица. Решение матричных уравненийСкачать

Комплексные числа

Правильный ответ выделен

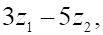
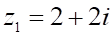
1. Сумма , показанное выше, если , показанное выше, равна

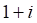
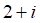
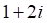
а. б. в. г.

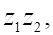
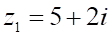
2. Произведение , показанное выше, если , показанное выше, равно

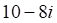
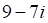
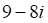
а. б. в. г.

Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Системы линейных уравнений

Правильный ответ выделен.

1. Система , показанных выше, линейных уравнений имеет

а. одно нулевое решение

б. бесконечно много решений

в. одно ненулевое решение

2. Частным решением системы линейных уравнений , показанных выше, является

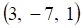
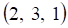
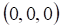
а. б. в. г.

3. Система линейных уравнений , показанных выше, имеет

а. одно решение£ два решения

б. бесконечно много решений

4. Матричное уравнение , показанных выше, с невырожденной квадратной матрицей А имеет решение

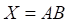
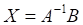
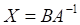
а. б. в. г.

5. Матричное уравнение AX=B с невырожденной квадратной матрицей А имеет решение

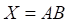
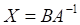
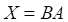
а. б. в. г.

Видео:Решение системы уравнений методом обратной матрицы.Скачать

Математический анализ. Дифференциальное исчисление

Правильный ответ выделен.

1 — тест. Производная функции (показано выше) равна

а.

2. Производная функции (показано выше) равна

б.

3. Производная функции (показано выше) равна

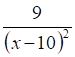
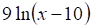
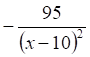
а. б. в. г.

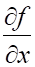
4. Частной производной (показано выше) для функции (показано выше) является

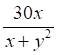
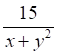
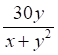
а. б. в. г.

5. Производная функции (показано выше) равна

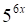
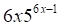
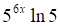
а. б. в. г.

6. Градиент функции (показано выше) равен

а.

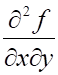
7. Смешанная производная (показано выше) для функции (показано выше) равна

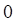
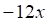
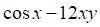
а. б. в. г.

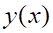
8. Достаточным условием выпуклости функции (показано выше) на интервале (показано выше) является

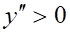
а. на

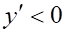
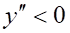
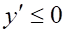
9. Достаточным условием убывания функции y(x) на интервале (a, b) является

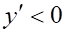
10. Точкой локального экстремума функции (показано выше) является

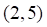
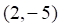
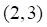
а. б. в. г.

11. Градиент функции (показано выше) равен

а.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Дифференциальные уравнения

Правильный ответ выделен.

тест — 1. Общим решением дифференциального уравнения (показано выше) является

а.

Видео:Обратная матрица (2 способа нахождения)Скачать

Интегральное исчисление

Правильный ответ выделен

1. Определенный интеграл (показано выше) равен

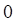
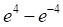
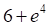
а. б. в. г.

2. Несобственный интеграл (показано выше) равен

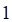
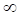
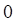
а. б. в. г.

3. Несобственный интеграл (показано выше) равен

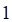
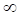
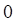
а. б. в. г.

4. Определенный интеграл (показано выше) равен

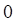
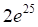
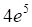
а. б. в. г.

5. Несобственный интеграл (показано выше) равен 1

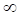
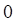
а. б. в.

Последовательности

Правильный ответ выделен.

1. Примером неограниченной последовательности является последовательность

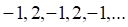
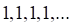
а. б. в. г.

2. Примером сходящейся последовательности является последовательность

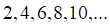
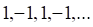
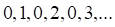
а. б. в. г.

3. Примером ограниченной последовательности является последовательность

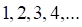
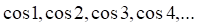
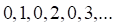
а. б. в. г.

4. Примером бесконечно малой последовательности является последовательность

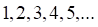
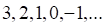
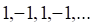
а. б. в. г.

5. Примером бесконечно большой последовательности является последовательность

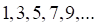
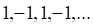
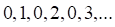
а. б. в. г.

6. Примером ограниченной последовательности является последовательность

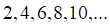
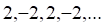
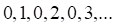
а. б. в. г.

7. Примером бесконечно малой последовательности является последовательность

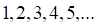
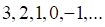
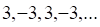
а. б. в. г.

8. Примером бесконечно большой последовательности является последовательность

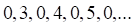
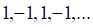
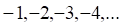
а. б. в. г.

9_тест. Примером ограниченной последовательности является последовательность

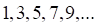
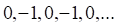
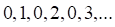
а. б. в. г.

Предел функции

Правильный ответ выделен

1. Предел (показано выше) равен

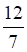
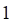
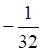
а. б. в. г.

2. Предел (показано выше) равен

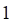
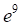
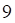
а. б. в. г.

3. Предел (показано выше) равен

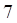
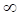
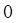
а. б. в. г.

Правильный ответ выделен

1. Радиус сходимости ряда (показано выше) равен

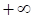
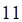
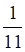
а. б. в. г.

2. Радиус сходимости ряда (показано выше) равен

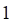
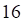
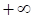
а. б. в. г.

3. Радиус сходимости ряда (показано выше) равен

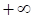
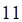
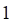
а. б. в. г.

Теория вероятностей

Правильный ответ выделен

1. Распределение дискретной случайной величины задано таблицей

Математическое ожидание M(X) равно

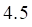
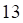
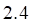
а. б. в. г.

2. Распределение дискретной случайной величины X задано таблицей

Математическое ожидание M(IXI) равно

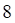
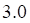
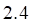
а. б. в. г.

3. Распределение дискретной случайной величины X задано таблицей

Дисперсия D(X) равна

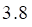
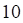
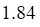
а. б. в. г.

тест_4. Распределение дискретной случайной величины X задано таблицей

Дисперсия D(X+4) равна

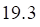
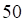
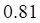
а. б. в. г.

Классическая вероятность

Правильный ответ выделен

1. Вероятность, что кубик упадет на грань «5», при условии, что выпадет нечетная грань, равна

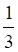
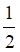
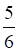
а. б. в. г.

2. В урне 11 находится красных и 4 черных шаров. Вероятность на удачу достать два красных шара равна

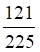
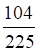
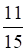
а. б. в. г.

3. Вероятность попадания в цель при одном выстреле равна 9/10. Вероятность того, что из двух выстрелов попали оба раза, равна

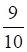
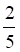
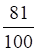
а. б. в. г.

4. Урна содержит 7 белых и 12 черных шаров. Вероятность наудачу достать первым белый шар, а вторым черный, равна

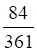
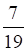
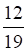
а. б. в. г.

5. Количество способов, которыми можно выбрать 4 экзаменационных билета из 9, равно