Ввиду краткости жизни мы не можем позволить себе роскошь решать уже решенные задачи.
Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Случайное фото
Цели и задачи курса
Дать современные представления об электромагнитных явлениях в различных типах материальных сред, познакомить с моделями сред. Практически освоить методы феноменологического и модельного описания электромагнитных явлений в средах, освоить принципы построения моделей сред.
I. Уравнения Максвелла.Уравнения Максвелла. Различные формы записи и материальные уравнения к ним. Материальные среды. Микро- и макрополя. Уравнения для микрополей и их усреднение. Индуцированные и сторонние плотности заряда и тока. Уравнения Максвелла в форме ВЕjr. Уравнения Максвелла в форме ВЕНD. Представление D и Н через векторы электрической и магнитной поляризации. Выражение индуцированных плотностей заряда и тока через векторы поляризации. Физический смысл векторов поляризации. Обобщенная электрическая индукция D и уравнения в форме ВЕD. Электромагнитные свойства сред с постоянными материальными тензорами (т.е. сред без пространственной и временной дисперсии).Материальные уравнения для сред с постоянными значениям материальных тензоров (постоянными в том смысле, что они не зависят от частоты и длины волны рассматриваемых полей). Связь различных материальных тензоров между собой для периодических в пространстве и во времени полей. Электромагнитные волны в средах с постоянными значениями материальных тензоров. Дисперсионные уравнения для волн при использовании различных форм записи уравнений Максвелла. Электромагнитные волны в изотропных и анизотропных средах. Проникновение слабо переменного поля в проводник (скин-эффект). II. Временная и пространственная дисперсии. Понятие о временной и пространственной дисперсии. Условия, когда ими можно пренебречь. Материальная среда в переменном поле. Запаздывание в реакции среды на поле — временная дисперсия.Общий вид материального уравнения с учетом временной дисперсии. Функция диэлектрической проницаемости. Среда, свойства которой не зависят от времени. Материальное уравнение для фурье-компонент полей. Частотная дисперсия. Спадающий характер функции диэлектрической проницаемости. Характерный временной масштаб спадания функции диэлектрической проницаемости и условие пренебрежения временной дисперсией. Пространственная дисперсия. Физические причины наличия пространственной дисперсии в средах. Условия пренебрежения пространственной дисперсией. Тензор диэлектрической проницаемости и его свойства. Общий вид материального уравнения типа D=D(E) для однородной среды, свойства которой не зависят от времени. Тензор диэлектрической проницаемости как функция коодинат и волнового вектора. Понятие о гиротропной среде. Способы определения тензора диэлектрической проницаемости. Комплексная электрическая восприимчивость среды. Соотношения Крамерса-Кронига. Материальное уравнение вида P=P(E) с учетом временной и пространственной дисперсии. Тензор комплексной электрической восприимчивости как функция волнового вектора. Вывод соотношений Крамерса-Кронига. Показать, что существование этих соотношений обусловлено учетом принципа причинности в материальном уравнении. Поглощение электромагнитной энергии в среде с дисперсией. Представление поглощаемого тепла, как тепла, поглощаемого за счет электрической и магнитной поляризаций. Вычисление среднего по времени тепла, поглощаемого за счет электрической поляризации, для периодических полей. Случай полей в виде плоских волн. Поглощение энергии в изотропной негиротропной среде. Нормальные электромагнитные волны в средах. Уравнения Максвелла для случая нормальных волн. Плоские волны. Система уравнений для напряженности электрического поля. Дисперсионное уравнение для нормальных волн. Общая схема решения задач о нормальных электромагнитных волнах в материальных средах. Изотропная негиротропная среда. Структура тензора диэлектрической проницаенмости и нормальные волны. Продольные и поперечные компоненты полей. Продольная и поперечная диэлектрические проницаемости. Продольные и поперечные нормальные волны и дисперсионные уравнения для них. В каком случае в изотропной среде существуют продольные волны. Гиротропная среда со слабой пространственной дисперсией. Тензор диэлектрической проницаемости и нормальные волны. Вращение плоскости поляризации. Тензор диэлектрической проницаемости для прозрачной изотропной гиротропной среды со слабой пространственной дисперсией. Нормальные волны. Вращение плоскости поляризации. Излучение нормальных электромагнитных волн заряженной частицей, движущейся в среде с постоянной скоростью. III. Простейшие модели конкретных материальных сред и электромагнитные свойства различных сред.III.1. Диэлектрики.Полярные диэлектрики. Дебаевская теория диэлектрической релаксации. Модельная оценка времени релаксации. Установление поляризации в полярном диэлектрике по Дебаю. Диэлектрическая проницаемость e(t) и e(w). Когда можно пренебречь временной дисперсией в полярных диэлектриках. Действительная и мнимая части e(w). Модель сферических частиц, вращающихся в вязкой жидкости, и оценка с ее помощью времени релаксации. Неполярные диэлектрики. Поглощение и аномальная дисперсия. Модель упруго связанных электронов и вычисление e(w).Условия пренебрежения временной дисперсией. Действительная и мнимая части e(w). Поглощение и аномальная дисперсия. Поправка Лоренц-Лоренца. Нормальные ЭМВ в неполярных диэлектриках. Поляритоны. Уравнения для нормальных волн. Продольные колебания и поперечные волны. Две ветви поперечных волн. Область непрозрачности. Связанные электромагнитные и упругие колебания. Поляритоны. III.2. Проводники.Проводники. Диэлектрическая проницаемость и проводимость. Модель. Вычисление e(w) и s(w). Связь e(w) с s(w). Условие пренебрежения временной дисперсией. Оптические свойства проводников. Проникновение поля в проводник на различных частотах. Комплексный показатель преломления для проводников. Уравнения для определения действительной и мнимой частей показателя преломления. Три области частот: область классического поглощения,промежуточная область и высокочастотная область. Нормальные ЭМВ в проводниках. Уравнения для нормальных ЭМВ. Продольные плазменные колебания и поперечные волны. Область непрозрачности. Оценка границы этой области для металлов. Проводящая среда в однородном магнитном поле. Проводимость металла в однородном магнитном поле. Эффект Холла. Диэлектрическая проницаемость проводника в однородном магнитном поле. Электромагнитные волны, распространяющиеся вдоль и поперек магнитного поля. Магнитная гиротропия, вращения плоскости поляризации в магнитном поле (эффект Фарадея). Низкочастотные спиральные электромагнитные волны в проводящей среде в магнитном поле. Нормальный скин-эффект в металлах. Уравнения, описывающие распределение поля в проводнике в квазистационарном случае. Скин-эффект. Классическая глубина скин-слоя. Аномальный скин-эффект в металлах. Необходимость учета пространственной дисперсии с ростом длины свободного пробега. Предельно аномальный скин-эффект. Концепция неэффективности и оценка на ее основе глубины проникновения поля в металл при аномальном скин-эффекте. Поверхностные электромагнитные волны. Электромагнитные волны, распространяющиеся вдоль плоской границы плазмы и вакуума. Дисперсионное уравнение. Глубина спадания поля при удалении от границы. Поляризация волн. III.3. Плазма.Плазма. Диэлектрическая проницаемость с учетом пространственной дисперсии. Продольные плазменные волны — плазмоны. Необходимость учета пространственной дисперсии в плазме. Гидродинамическая модель плазмы и получение зависимости тензора диэлектрической проницаемости от частоты на ее основе . Нормальные ЭМВ. Продольные плазменные волны. Адиабатический процесс. Дебаевский радиус и его смысл. Экранирование поля заряда в плазме. III.4. Сверхпроводники.Сверхпроводники. Эффект Мейсснера и невозможность его объяснения в модели идеального проводника. Уравнение Лондонов. Идеальный проводник. Материальное уравнение. Уравнения, определяющие распределение переменной части магнитного поля. «Вмораживание» магнитного поля в идеальный проводник. Эффект Мейсснера. Уравнение Лондонов и объяснение его на основе эффекта Мейсснера. Сохранение магнитного потока. Природа сверхпроводящего состояния. Куперовские пары и щель в энергетическом спектре. Квантовое обобщенное уравнение Лондонов. Квантование магнитного потока. Роль пространственной дисперсии в сверхпроводниках. Лондоновские и пиппардовские сверхпроводники. Оценка глубины проникновения магнитного поля в пиппардовский сверхпроводник. Высокотемпературные сверхпроводники. III.5. Магнетики.Магнетики. Уравнение движения для намагниченности. Магнитный резонанс. Модель. Уравнение для намагниченности. Поведение намагниченности в постоянном поле — процессия намагниченности. Поведение намагниченности в переменном поле. Магнитная восприимчивость. Магнитный резонанс. Ферромагнетики. Эффективное поле. Магнитная восприимчивость с учетом пространственной дисперсии. Ферромагнетизм. Молекулярное поле Вейса. Природа молекулярного поля. Обменное взаимодействие. Необходимость учета пространственной дисперсии. Уравнение движения для намагниченности с учетом неоднородного обменного взаимодействия и вычисление на его основе магнитной восприимчивости. Магнитный резонанс в неоднородном поле. Спиновые волны в ферромагнетиках. Уравнения для низкочастотных нормальных ЭМВ в магнитостатическом приближении. Дисперсионное уравнение. Закон дисперсии для спиновых волн.
Темы практических занятий
Различные формы уравнений Максвелла. ЭМП в средах без дисперсии. Диэлектрическая проницаемость газа свободных электронов. ЭМВ в средах (частные случаи). КР N 1. Диэлектрическая проницаемость газа свободных электронов в МП. ЭМВ в металлах в магнитном поле. Вращение плоскости поляризации. ЭМВ в неполярных диэлектриках. КР N 2. Компьютерный эксперимент: «Падение ЭМВ на плоскую границу раздела двух сред». Компьютерный эксперимент «Определение характеристик неизвестного проводника в оптических экспериментах». ЭМ свойства плоскопараллельного слоя. Поверхностные ЭМВ. Потери энергии быстрых заряженных частиц. КР N 3.
Туров Е.А. Электродинамика /конспект лекций/. Свердловск, УрГУ, 1973 г. Туров Е.А. Материальные уравнения электродинамики. М. «Наука», 1983. Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М. «Наука» 1982. Силин В.П., Рухадзе А.А. Электромагнитные свойства плазмы и плазмоподобных сред. М., «Наука», 1965. Агранович В.М., Гинзбург В.Л. Кристаллооптика с учетом пространственной дисперсии. М., «Наука» 1979. Гроссе П. Свободные электроны в твердых телах. М. «Мир» 1982. Бредов М.М., Румянцев В.В., Топтыгин И.Н. Классическая электродинамика, М. Наука, 1985. Рязанов М.И. Электродинамика конденсированного вещества. М. «Наука», 1984.
Видео:Квантово-механический вывод диэлектрической проницаемости сплошной средыСкачать

Понятие о тензоре диэлектрической проницаемости
Вы будете перенаправлены на Автор24
Видео:1.2 Материальные уравнения, векторы поляризованности и намагниченности средСкачать

Материальное уравнение для изотропной среды
Мы помним, что материальное уравнение для изотропной среды, можно записать как:
где $varepsilon $ — диэлектрическая проницаемость среды, которая характеризует свойства диэлектрика, зависит от температуры и плотности.
Рассмотрим однородную, непроводящую и магнитоизотропную среду, что означает, вектор электрического смещения не будет параллелен вектору напряженности. В этом случае, связь (1) запишем в виде:
или тоже самое, но более компактно:
где индексы i,j — нумеруют компоненты по осям декартовой системы координат ($i=x, y,z;;j=x, y,z. )$), $_$ — тензор диэлектрической проницаемости вещества. Девять величин $_, _,_,dots ,$ — являются постоянными среды и составляют тензор диэлектрической проницаемости. Соответственно, вектор смещения ($overrightarrow$) равен произведению тензора диэлектрической проницаемости на вектор напряженности электрического поля ($overrightarrow$). При формальной тензорной записи знак суммы опускают, суммирование обозначают двукратным повторением индекса (в нашем случае индекс j), то есть:
Тензор диэлектрической проницаемости симметричен при любом значении поля, то есть можно записать следующее:
Симметрия тензора $_$- необходимое и достаточное условие для выполнения закона сохранения энергии. Из девяти компонент тензора диэлектрической проницаемости только шесть независимы. Симметричность рассматриваемого нами тензора позволяет привести выражение для плотности энергии электрического поля к такой форме, при которой сохраняются только квадраты компонент поля и отсутствуют их произведения. В такой системе (а она называется системой главных диэлектрических осей) материальные уравнения электрического поля имеют вид:
Видео:1.3 Классификация сред в электродинамикеСкачать

Плотность электрической энергии
Выражение для плотности электрической энергии для рассматриваемого нами случая будет иметь вид:
где величины $_x,_y,_z$ — называются главными диэлектрическими проницаемостями. Из приведенных выше формул следует, что векторы $overrightarrow$ и $overrightarrow$ всегда имеют разные направления, если направление вектора напряженности поля не совпадает с одной из главных осей или все главные диэлектрические проницаемости не равны друг другу.
В случае изотропной среды диэлектрическая проницаемость не является постоянной вещества, она зависит от частоты и точно так же как в анизотропной среде шесть компонент тензора диэлектрической проницаемости $_$ изменяются в зависимости от частоты. Следовательно, меняются не только величины главных диэлектрических проницаемостей, $_x,_y,_z$, но и направления главных осей. Такое явление называется дисперсией осей. Необходимо заметить, что оно может возникать только в тех кристаллических структурах, симметрия которых не позволяет выделить предпочтительную совокупность ортогональных осей направлений.
Дисперсию можно не учитывать, если рассматривать монохроматические волны, в таком случае $_$ являются постоянными, зависящими только от свойств вещества.
Связь тензоров диэлектрической проницаемости и диэлектрической восприимчивости имеет вид:
где $_- $единичный тензор, который равен:
Готовые работы на аналогичную тему
Задание: Докажите, что тензор диэлектрической проницаемости симметричен. Считать, что поглощение отсутствует, магнитное поле однородно и изотропно.
В качестве основы для доказательства используем выражения для плотности энергии электрического ($w_e$) и магнитного полей ($w_m$):
где $H_iH_j$- компоненты вектора напряжённости магнитного поля.
Выражение для вектора Умова — Пойнтинга ($overrightarrow$):
Первое и второе уравнения из системы уравнений Максвелла:
Уравнение (1.5) системы умножим на вектор напряженности электрического поля ($overrightarrow$), уравнение (1.4) умножим на вектор напряженности магнитного поля ($overrightarrow$), сложим два полученных выражения при этом опустим ток проводимости, получим:
[overrightarrowrotoverrightarrow-overrightarrowrotoverrightarrow=overrightarrowcdot overrightarrow+overrightarrowcdot frac<partial overrightarrow>+overrightarrowcdot frac<partial overrightarrow> (1.6)] [-divoverrightarrow=-divleft[overrightarrowtimes overrightarrowright]=overrightarrowcdot dot<overrightarrow>+overrightarrowcdot dot<overrightarrow>=_0E_i_dot+frac_0frac
где $overrightarrow$ — вектор магнитной индукции. При преобразовании дивергенции векторного произведения мы использовали известное векторное равенство:
[divleft[overrightarrowtimes overrightarrowright]=overrightarrowrotoverrightarrow-overrightarrowrotoverrightarrow left(1.8right).]
Исходя из уравнения (1.2) мы получили, что в уравнении (1.7) вторым слагаемым является:
Так как мы условились, что среда является однородной и изотропной для магнитного поля, то такая производная равна нулю. Изучим производную по времени от плотности энергии электрического поля:
Выражение $_0sumlimits_<E_i_dot>$ будет представлять собой скорость изменения плотности энергии электрического поля только если:
Мы понимаем, что изменение индексов в выражении (1.12) фиктивно, так как они принимают одни и те же значения (x,y,z). Из уравнения (1.12) следует, что:
Что требовалось доказать.
Задание: Покажите, используя тензор диэлектрической проницаемости, что векторы $overrightarrow $и $overrightarrow$ не коллинеарны в неизотопном кристалле.
Анизотропная среда характеризуется тензором диэлектрической проницаемости второго ранга:
Это означает, что каждая составляющая вектора $overrightarrow$ выражается через все три составляющие вектора напряженности электрического поля:
Выберем главные оси X,Y,Z и зафиксируем их по отношению к кристаллу. В таком случаем можно записать:
Система (2.3) означает, что тензор диэлектрической проницаемости приведен к виду:
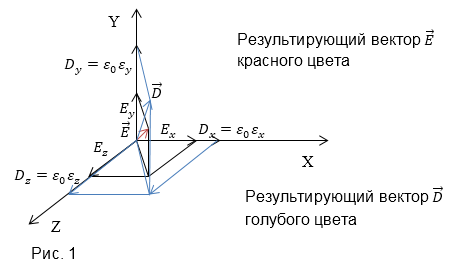
С точки зрения математики — это диагонализация матрицы (2.1). Если $_xne _yne _z$, то при умножении составляющих вектора $overrightarrow$ на соответствующие компоненты тензора диэлектрической проницаемости, то компоненты вектора электрического смещения (2.3) не совпадут по направлению с вектором $overrightarrow$. (рис.1).
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 08.12.2021
Видео:Физика - Магнитное полеСкачать

Магнитная и диэлектрическая проницаемость
Читайте также:
|



 ,
,