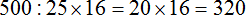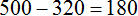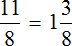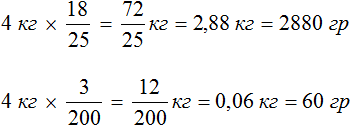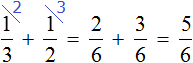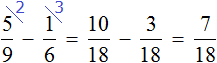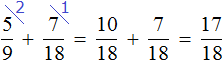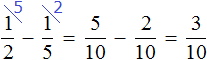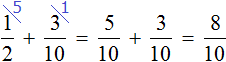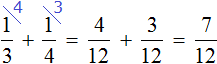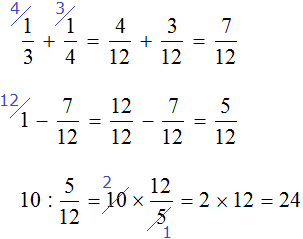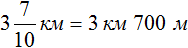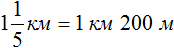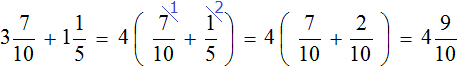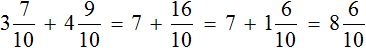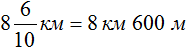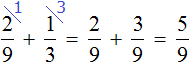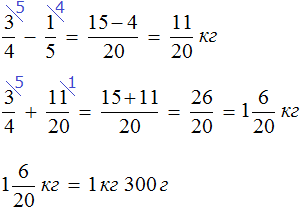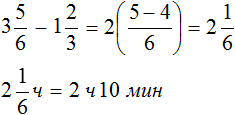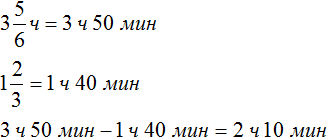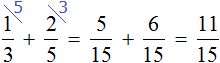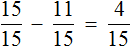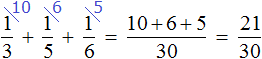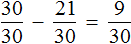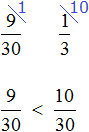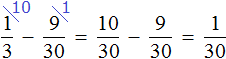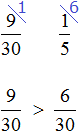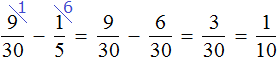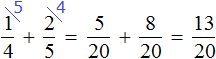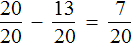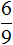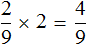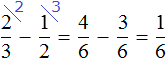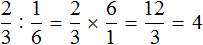Разделы: Математика
Класс: 6
Цель: Закрепить навыки решения задач на дроби, проверить умения решения задач путём самостоятельной работы.
Ход урока
1. Задача на внимание (показывается на несколько минут, затем убирается и ребята по памяти отвечают на вопросы учителя)
- Какие геометрические фигуры вы запомнили?
- Назовите дробь, записанную в окружности
- Каков цвет окружности?
- Есть ли среди дробей дробь с числителем 1?
- В какой фигуре она записана?
- Назовите эту дробь.
- Каков цвет квадрата?
- Каков цвет треугольника?
- Назовите дробь, записанную в нём.
2. Устная работа
в) Логическая задача
3. Решение задач на дроби
№1. На ветке сидели 12 птиц; 
12 : 3 • 2 = 8 (птиц) улетело
№2. 
21 : 3 • 5 = 35 (деревьев) – всего в парке
Ответ. 35 деревьев.
№3. В книге 120 страниц. Маша прочитала в первый день 
- 120 : 3 • 2 = 80 (стр.) – в первый день
- 20 – 80 = 40 (стр.) – оставшаяся часть
- 40 : 4 = 10 (стр.) – во второй день
- 120 – (80 + 10) = 30 (стр.) – осталось прочитать
Ответ. 30 страниц.
№4. В прошлом месяце цена товара составляла 90 р. Теперь она понизилась на 
- 90 : 10 = 9 (р.) – понижение цены
- 90 – 9 = 81 (р.) – цена товара
№5. На праздник закупили синие, зелёные и красные шарики. Синих – 20 штук, причём они составили 
Сколько зелёных шариков?
- 20 : 5 • 12 = 48 (шариков) – всего
- 20 + 2 = 22 (шарика) – красные
- 48 – (20 + 22) = 6 (шариков) – зелёные
Ответ: 6 шариков.
№6. Мама покупала конфеты для новогодних подарков. На покупку шоколадных конфет она израсходовала 
- 700 : 5 • 2 = 280 (р.) – шоколадные конфеты
- 120 • 2 = 240(р.) – карамель
- 45 • 2 = 90 (р.) – шоколад
- 700 – (280 + 240 + 90) = 610 (р.) – осталось
Ответ. 610 р., хватит.
№ 7. В первый день в магазине продали 150 кг яблок, что составило 60% всех привезённых яблок. Во второй 
4. Самостоятельная работа
1. Запиши верные равенства:
2. В классе 24 ученика. Девочки составляют 
3. Потратили 600 рублей. Это составило 
1. Запиши верные равенства:
2. Сыну 10 лет. Его возраст составляет 
3. В спортивной секции занимается 35 человек, 
5. Домашнее задание
1. Автотуристы за три дня проехали 360 км; в первый день они проехали 

2. (Старинная задача) Приходит пастух с 70 быками. Его спрашивают:
— Сколько приводишь ты из своего многочисленного стада?
— Я привожу две трети от трети скота. Сочти!
- Задачи по теме «Решение задач, составлением уравнения» (6 класс)
- Решение задач с помощью уравнений
- Введение
- Алгоритм решения текстовых задач с помощью уравнений
- Примеры решений
- Задачи для самостоятельного решения
- Задачи на дроби
- Задачи на дроби
- Задачи для самостоятельного решения
- 30 thoughts on “Задачи на дроби”
- 🔍 Видео
Видео:Математика 6 класс (Урок№51 - Решение задач с помощью уравнений. Часть 1.)Скачать

Задачи по теме «Решение задач, составлением уравнения» (6 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
Столичный центр образовательных технологий г. Москва
Получите квалификацию учитель математики за 2 месяца
от 3 170 руб. 1900 руб.
Количество часов 300 ч. / 600 ч.
Успеть записаться со скидкой
Форма обучения дистанционная
Видеолекции для
профессионалов
- Свидетельства для портфолио
- Вечный доступ за 120 рублей
- 311 видеолекции для каждого
Задачи на составление уравнения (6класс)
- Кофейник и две чашки вмещают 740 г воды. В кофейник входит на 380 г больше, чем в чашку. Сколько граммов воды вмещает кофейник?
- За три дня было продано 830 кг апельсинов. Во второй день продали на 30 кг меньше, чем в первый, а в третий – в 3 раза больше, чем во второй. Сколько килограммов апельсинов было продано в первый день?
- Велосипедист проехал 43 км. По проселочной дороге он проехал в 3 раза большее расстояние, чем по лесной тропинке, а по тропинке на 35 км меньше, чем по шоссе. Какой длины была каждая часть пути велосипедиста?
- В двух альбомах 750 марок, причем в первом альбоме имевшихся марок составляли иностранные марки. Во втором альбоме иностранные марки составляли 0,9 имевшихся там марок. Сколько всего марок было в каждом альбоме, если число
иностранных марок в них было одинаково?
- В одной бочке 110 л бензина, а в дугой 130 л. После того как из второй бочки взяли в 2 раза больше бензина, чем из первой, в первой оказалось на 5 л больше, чем во второй. Сколько литров бензина взяли из каждой бочки?
- В летние каникулы я проехал на поезде на 120 км больше, чем проплыл на теплоходе. Если бы я проехал на поезде в 4 раза больше, а на теплоходе проплыл в 8 раз больше, чем в действительности, то общий путь составил бы 1200 км. Сколько километров я проплыл на теплоходе?
- В клетке сидят фазаны и кролики. У них 19 голов и 62 ноги. Сколько фазанов и сколько кроликов в клетке?
- – Скажи мне знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы
– Вот сколько, – ответил Пифагор, – половина изучает математику, четверть – природу, седьмая часть проводит время в размышлении, и, кроме того, есть еще три женщины.
- В одной пачке было в 2,5 раза больше тетрадей, чем в другой. Когда из второй пачки переложили в первую 5 тетрадей, то во второй стало в 3 раза меньше тетрадей, чем в первой. Сколько тетрадей было в каждой пачке первоначально?
- В первом вагоне трамвая ехало в 1,5 раза больше пассажиров, чем во втором. После того как из первого вагона вышли 5 пассажиров, а во второй вошли 3 пассажира, в обоих вагонах пассажиров стало поровну. Сколько пассажиров ехало в каждом вагоне первоначально?
- В бидоне было в 2 раза больше молока, чем в банке. После того как из банки взяли 2л, а из бидона 3 л, в банке осталось молока в 4,5 раза меньше, чем в бидоне. Сколько литров молока было в бидоне и в банке вместе?
- В парке 20% всех деревьев составляют березы, третью часть – клены, дубов на 18 больше, чем кленов, а остальные 94 дерева – липы. Сколько всего деревьев в этом парке?
- На овощную базу завезли 140 т картофеля и 80 т капусты. Потом с базы ежедневно вывозили картофеля в 2,5 раза больше, чем капусты, и через 8 дней их количество на базе стало одинаковым. Сколько всего тонн овощей вывозили ежедневно с базы?
- Пассажирский поезд проходит расстояние между двумя городами за 10 ч, а товарный – за 12 ч 30 мин. Товарный поезд идет со скоростью на 28 км/ч меньшей, чем пассажирский. Каково расстояние между городами?
- В питомнике было 450 саженцев яблонь и 180 саженцев слив. За день купили в 4 раза больше яблонь, чем слив, и саженцев слив осталось на 150 меньше, чем яблонь. Сколько всего саженцев купили за этот день?
- В первом бидоне было в 4 раза больше оливкового масла, чем во втором. Когда из первого бидона перелили во второй 1,6 л, то во втором бидоне стало в 1,5 раза больше масла, чем в первом. Сколько литров масла стало в каждом бидоне?
Видео:Как решать задачи по математике в 6 классе на части (дроби) с помощью уравнения и без уравнения.Скачать

Решение задач с помощью уравнений
Тема урока: § 6. Решение задач с помощью уравнений. Приведены все необходимые и достаточные сведения для решения текстовых задач с помощью составления уравнений.
Видео:Решение задач с помощью уравнений. Видеоурок 29. Математика 6 классСкачать

Введение
В школьной математике есть целый кладезь текстовых задач, которые решаются универсальным методом построения уравнения (модели) исходя из условия.
Сам факт того, что огромное количество самых разнообразных задач поддаются решению с помощью составления линейного уравнения, говорит нам, что метод решений является действительно универсальным.
Обычно условия задач удается перевести на математический язык. Полученное уравнение — это следствие перевода нашего условия с русского языка на язык алгебры. Зачастую фактической стороной повествования задачи является описание реальной ситуации, какого либо процесса, события.
Чтобы получить ответ — уравнение нужно решить, полученный корень уравнения будет являться решением, разумеется необходимо еще проверить, не является ли результат противоречивым относительно условия.
Видео:Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 2 часть. 6 класс.Скачать

Алгоритм решения текстовых задач с помощью уравнений
Для решения задачи с помощью уравнения делают следующие действия:
- Обозначают некоторое неизвестное буквой и, пользуясь условием, составляют уравнение.
- Решают уравнение.
- Истолковывают результат.
Видео:Уравнения с дробями 6 класс (задания, примеры) - как решать?Скачать

Примеры решений
Задача 1.
В мешке было в 3 раза меньше монет, чем в сундуке. После того как из мешка переложили 24 монеты, в сундуке их стало в 7 раз больше, чем в мешке. Сколько было монет в мешке и сколько в сундуке?
Пусть $x$ — количество монет в мешке, а значит в сундуке: $3x$ монет. После того, как из мешка переложили $24$ монеты, в сундуке стало: $3x+24$, а в мешке $x-24$. И если в сундуке их стало в $7$ раз больше чем в мешке, то имеем: $3x+24=7(x-24)$.
Ну вот мы и составили уравнение (математическую модель), осталось решить уравнение относительно $x$ и записать ответ.
Решим полученное уравнение: $3x+24=7(x-24)$. Легко увидеть, что уравнение является линейным (узнать как решаются линейные уравнения можно тут.)
Раскроем скобки в правой части уравнения: $3x+24=7x-7cdot 24$. Перенесём все слагаемые содержащие переменную в правую часть, а всё что не содержит $x$ в левую, получим: $24+7cdot 24=7x-3x$. После упрощения получили $192=4x$, разделим обе части уравнения на коэффициент при неизвестном, т.е на $4$, тогда получим $x=48$.
Осталось истолковать ответ.
За переменную $x$ мы обозначали количество монет в мешке, значит в сундуке в три раза больше т.е $3x$.
Монет в мешке: $48$
Монет в сундуке: $48cdot 3=144$
Задача 2.
Купили 3600 кг муки и высыпали её в три мешка. В первый мешок муки вошло в 3 раза больше, чем во второй, а в третий мешок насыпали 800 кг муки. Сколько муки насыпали в первый и сколько во второй мешок?
Пусть в первый мешок насыпали $3x$ кг муки, тогда во второй мешок насыпали $x$ кг. Если сложим количество кг в каждом мешке, то получим $3600$ кг муки. Имеем: $3x+x+800=3600$, решим уравнение классическим методом.
Все слагаемые содержащие $x$ оставим слева, а всё остальное перенесём в правую часть равенства: $3x+x=3600-800$, упростим обе части; $4x=2800$ поделим обе части равенства на $4$ и получим ответ: $x=700$.
Ответ.
За переменную $x$ мы обозначали количество муки во втором мешке, по условию в первом в три раза больше.
Муки в первом мешке: $700cdot 3=2100$ кг.
Муки во втором мешке: $700$ кг.
Задача 3.
В первом мешке в 4 раза больше картофеля, чем во втором. После того, как из одного мешка взяли 40 кг картофеля, а во второй насыпали ещё 5 кг, в обоих мешках картофеля стало поровну. Сколько килограммов картофеля было во втором мешке.
Пусть во втором мешке $x$ кг картофеля, тогда в первом мешке $4x$ кг. Из первого взяли $40$ кг, тогда в первом стало: $4x-40$. Во второй мешок насыпали $5$ кг и теперь в нём: $x+5$ кг картошки. Нам известно, что после этих изменений количество картофеля в мешках стало поровну, запишем это с помощью линейного уравнения:
Решим это линейное уравнение. Все слагаемые содержащие переменную перенесём влево, а свободные члены вправо и получим:
Избавимся от коэффициента при неизвестном и получим ответ:
Ответ.
За переменную $x$ мы обозначали количество кг картошки во втором мешке, по условию в первом в четыре раза больше.
Картошки в первом мешке: $15cdot 4=60$ кг.
Картошки во втором мешке: $15$ кг.
Задача 4.
По шоссе едут две машины с одной и той же скоростью. Если первая увеличит скорость на 20 км/ч, а вторая уменьшит скорость на 20 км/ч, то первая за 2 часа пройдёт то же самое расстояние, что и вторая за 4 часа. Найдите первоначальную скорость машин.
Пусть машины едут со скоростью $v$ км/ч, тогда после ускорения первой машины её скорость стала: $v+20$ км/ч, а скорость второй машины после замедления стала: $v-20$ км/ч. Нам известно по условию, что после изменения скоростей машин, первая проходит за два часа ровно столько, сколько вторая за четыре, тогда имеем:
По известной нам формуле $S=vt$ ($S$ — расстояние, $v$ — скорость, $t$ — время)
Сократим обе части равенства на $2$, тогда получим: $v+20=2(v-20)$. Раскроем скобки в правой части уравнения и сгруппируем все переменные в правой части равенства.
Ответ.
В качестве неизвестной величины в задаче мы взяли $v$ (первоначальную скорость машин).
Первоначальная скорость машин: $v=60$ км/ч.
Задача 5.
В первую бригаду привезли раствора цемента на 50 кг меньше, чем во вторую. Каждый час работы первая бригада расходовала 150 кг раствора, а вторая – 200кг. Через 3 ч работы в первой бригаде осталось раствора в 1,5 раза больше, чем во второй. Сколько раствора привезли в каждую бригаду?
Пусть во вторую бригаду привезли $x$ кг раствора цемента, тогда в первую бригаду привезли $x-50$ кг. Через 3 часа работы у первой бригады осталось $x-50-3cdot 150$ кг цемента, а у второй $x-3cdot 200$ кг.
По условию известно, что через 3 часа работы в первой бригаде осталось в 1,5 раза больше цемента, чем во второй, тогда имеем:
$$x-50-3cdot 150=1,5(x-3cdot 200)$$
Осталось решить данное уравнение относительно $x$ и истолковать ответ.
Упростим и раскроем скобки в правой части, тогда получим:
Если вам неудобно работать с десятичными дробями, то вы всегда можете их переводить в рациональный вид: $1,5=frac=frac$.
Запишем с учётом перевода дробей и упростим:
Перенесём слагаемые содержащие переменную в правую сторону, а всё остальное в левую:
Домножим обе части на 2 и получим ответ:
Ответ.
В качестве переменной в задаче мы взяли $x$ (кол-во кг цемента который привезли во вторую бригаду), по условию в первую привезли на 50 кг меньше, а значит $x-50$
Кол-во цемента в первой бригаде: $800-50=750$ кг.
Кол-во цемента во второй бригаде: $800$ кг.
Видео:Решение задач с помощью уравнений. 6 классСкачать

Задачи для самостоятельного решения
По контракту работникам причитается 48 франков за каждый отработанный день, а за каждый неотработанный день с них вычитается по 12 франков. Через 30 дней выяснилось, что работникам ничего не причитается. Сколько дней они отработали в течение этих 30 дней?
Пусть работники отработали $n$ дней, тогда $30-n$ дней они не отработали.
В итоге мы понимаем, что за $n$ рабочих дней они зарабатывают $48n$ франков и с них вычитается за $30-n$ не отработанных дней по $12(30-n)$ франков. Тогда ясно, что: $48n-12(30-n)=0$
Ответ: Рабочие отработали 6 дней.
Кирпич весит фунт и полкирпича. Сколько фунтов весит кирпич?
Пусть целый кирпич весит весит $k$ фунтов, тогда имеем:
1 фунт и половина кирпича = целый кирпич.
Бутылка с пробкой стоит 10 копеек, причем бутылка на 9 копеек дороже пробки. Сколько стоит бутылка без пробки?
Пусть бутылка стоит $b$ копеек, а пробка $p$ копеек, тогда:
$b+p=10$ и $b=p+9$, подставив значение $b$ в первое равенство — получим:
Т.е пробка стоит пол копейки, тогда бутылка $9,5$ копеек.
Ответ: 9,5 копеек стоит бутыка без пробки.
На свитер, шапку и шарф израсходовали 555 г шерсти, причем на шапку ушло в 5 раз меньше шерсти, чем на свитер, и на 5 г больше, чем на шарф. Сколько шерсти израсходовали на каждое изделие?
Пусть на свитер потратили $5x$ г шерсти, тогда на шапку ушло $x$ г и на шарф потребовалось $x-5$ г, имеем:
Ответ: На шапку ушло $80$ г, на свитер $5cdot 80=400$ г, на шарф $80-5=75$ г.
Три пионерских звена собрали для школьной библиотеки 65 книг. Первое звено собрало на 10 книг меньше, чем второе, а третье — 30% того числа книг, которое собрали первое и второе звено вместе. Сколько книг собрало каждое звено?
Пусть второе звено собрало $x$ книг, тогда первое собрало $x-10$ книг, а третье $0,3(2x-10)$, имеем:
$$2x-10+0,3cdot 2x-0,3cdot 10=65$$
$$2x+0,3cdot 2x=65+10+0,3cdot 10$$
Ответ: Первое звено собрало $30-10=20$ книг, второе $30$ книг, третье $0,3(60-10)=15$ книг.
Видео:Математика 6 класс. Решение задач на составление уравненийСкачать

Задачи на дроби
Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на дроби.
Прежде чем решать задачи на дроби, необходимо досконально изучить все темы, касающиеся дробей. Ниже приведен список уроков, которые можно повторить.
Каждая задача, приведенная в данном уроке, относится к категории элементарных. Если какая-то задача непонятна, это указывает на то, что предыдущий материал усвоен недостаточно хорошо.
Видео:Решить уравнение с дробями - Математика - 6 классСкачать

Задачи на дроби
Задача 1. В классе 
Решение
Если 
Задача 2. В классе школьников составляют отличники, 

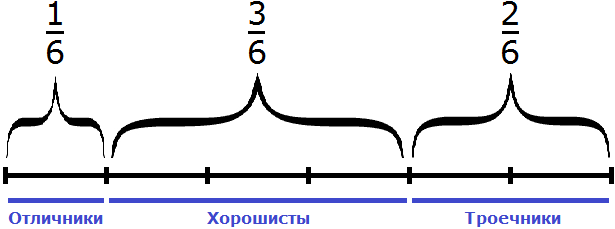
Задача 3. В классе 24 школьника. школьников составляют отличники, 

Решение
24 : 6 × 1 = 4 × 1 = 4 (отличника)
24 : 6 × 3 = 4 × 3 = 12 (хорошистов)
24 : 6 × 2 = 4 × 2 = 8 (троечников)
Проверка
4 + 12 + 8 = 24 (школьника)
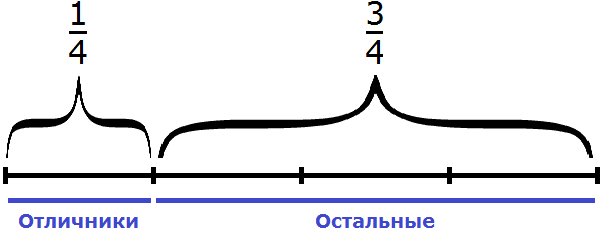
Задача 4. В классе школьников составляют отличники, 
Решение
Школьники разделены на 6 частей. На одну из частей приходятся отличники, на три части — хорошисты. Нетрудно догадаться, что на остальные две части приходятся троечники. Значит 
Не приводя рисунков можно сложить дроби и 

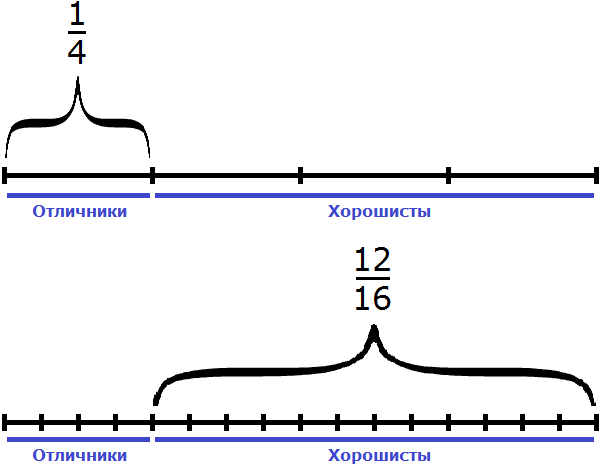
Задача 5. В классе 16 школьников. Из них 
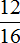
Решение
16 : 4 × 1 = 4 × 1 = 4 (отличника)
16 : 16 × 12 = 1 × 12 = 12 (хорошистов)
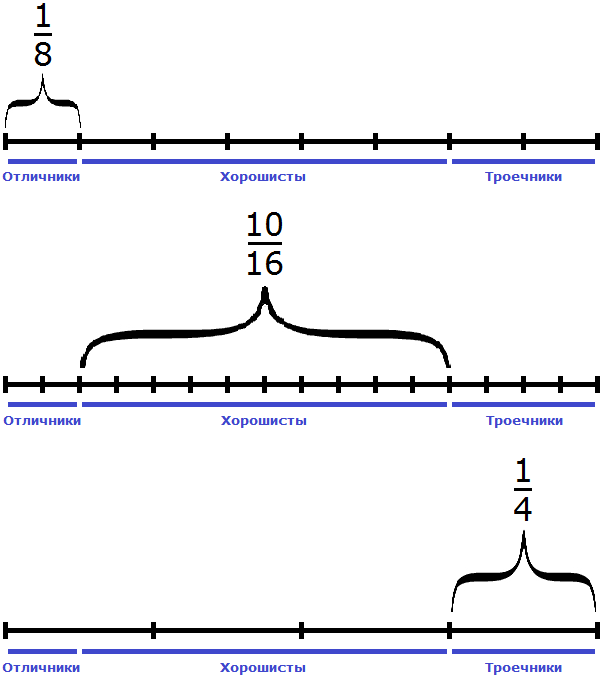
Задача 6. В классе 16 школьников. Из них 
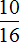

Решение
16 : 8 × 1 = 2 × 1 = 2 (отличника)
16 : 16 × 10 = 1 × 10 = 10 (хорошистов)
16 : 4 = 4 (троечника)
Задача 7. Из зерен пшеницы производят полтавскую крупу, масса которой составляет 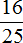
Решение
Найдем 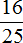
Теперь найдем массу кормовых отходов. Для этого вычтем из 500 ц массу полтавской крупы:
Значит из 500 центнеров зерен пшеницы можно получить 320 центнеров полтавской крупы и 180 центнеров кормовых отходов.
Задача 8. Килограмм сахара стоит 88 рублей. Сколько стоит 



Решение
1) 
44 × 1 = 44 рубля
2) 

22 × 1 = 22 рубля
3) Дробь 


4) Дробь 
Одиннадцать восьмых это один целый килограмм и 


Стоимость 

Но выделив целую часть можно хорошо понять, как сформировалась цена на 
Задача 9. Финики содержат 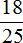
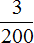
Решение
Узнаем сколько граммов сахара содержится в одном килограмме фиников. Один килограмм это тысяча грамм. Найдем 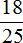
В одном килограмме фиников содержится 720 грамм сахара. Чтобы узнать сколько грамм сахара содержится в четырех килограммах, нужно 720 умножить на 4
Теперь узнаем сколько минеральных солей содержится в 4 килограммах фиников. Но сначала узнаем сколько минеральных солей содержится в одном килограмме. Один килограмм это тысяча грамм. Найдем 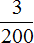
В одном килограмме фиников содержится 15 грамм минеральных солей. Чтобы узнать сколько грамм минеральных солей содержится в четырех килограммах, нужно 15 умножить на 4
Значит в 4 кг фиников содержится 2880 грамм сахара и 60 грамм минеральных солей.
Решение для данной задачи можно записать значительно короче, двумя выражениями:
Суть в том, что от 4 килограмм нашли 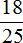
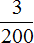
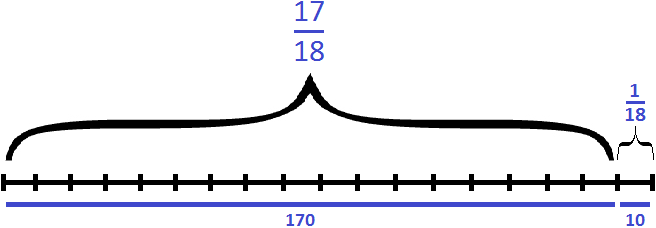
Задача 10. Поезд прошел 840 км, что составляет 
Решение
В задаче говорится, что 840 км это 

А поскольку весь путь состоит из семи частей, то расстояние всего пути можно найти, умножив 210 на 7:
210 × 7 = 1470 км.
Теперь ответим на второй вопрос задачи — какое расстояние осталось пройти поезду? Если длина пути 1470 км, а пройдено 840, то оставшийся путь равен 1470−840, то есть 630
Задача 11. Одна из групп, покорившая горную вершину Эверест, состояла из спортсменов, проводников и носильщиков. Спортсменов в группе было 25, число проводников составляло 
Решение
Спортсменов группе 25. Проводников составляет 

Спортсменов и проводников вместе — 45 человек. Это число составляет 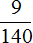
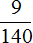
45 : 9 × 140 = 5 × 140 = 700
Задача 12. В школу привезли 900 новых учебников, из них учебники по математике составляли 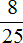
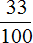
Узнаем сколько составляют учебники по математике:
900 : 25 × 8 = 288 (книг по математике)
Узнаем сколько учебников по русскому языку:
900 : 100 × 33 = 297 (книг по русскому языку)
Узнаем сколько учебников по литературе. Для этого из общего числа книг вычтем учебники по математике и по русскому:
900 – (288+297) = 900 – 585 = 315
Проверка
288 + 297 + 315 = 900
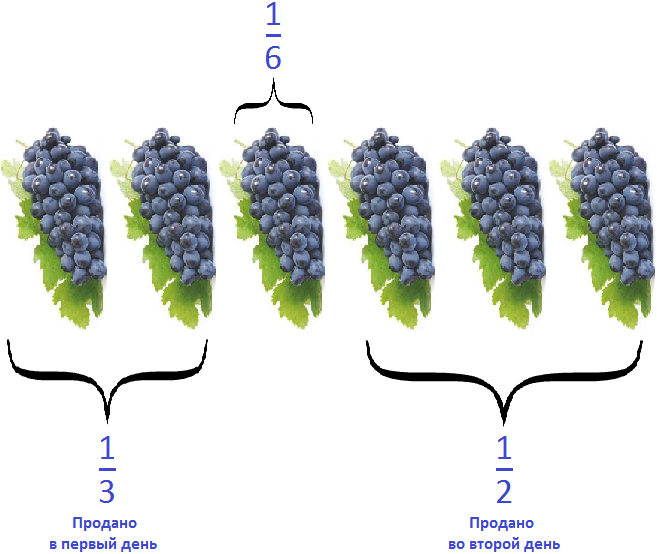
Задача 13. В первый день продали 

Решение
За два дня продали 

Можно представить поступивший в магазин виноград в виде шести гроздей. Тогда 


Задача 14. Вера в первый день прочитала 
Решение
Определим часть книги, прочитанной во второй день. Сказано, что во второй день прочитано на меньше, чем в первый день. Поэтому из 
Во второй день Вера прочитала 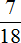
За два дня Вера прочитала 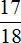
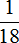
Сделаем проверку. Предположим что книга, которую читала Вера, имела 180 страниц. В первый день она прочла 

180 : 9 × 5 = 100 (страниц)
Во второй день Вера прочитала на меньше, чем в первый. Найдем от 180 страниц, и вычтем полученный результат из 100 листов, прочитанных в первый день
180 : 6 × 1 = 30 × 1 = 30 (страниц)
100 − 30 = 70 (страниц во второй день)
Проверим, являются ли 70 страниц 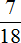
180 : 18 × 7 = 10 × 7 = 70 (страниц)
Теперь ответим на второй вопрос задачи — успела ли Вера прочитать все 180 страниц за два дня. Ответ — не успела, поскольку за два дня она прочла только 170 страниц
100 + 70 = 170 (страниц)
Осталось прочесть еще 10 страниц. В задаче в роли остатка у нас была дробь 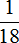
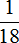
180 : 18 × 1 = 10 × 1 = 10 (страниц)
Задача 15. В одном пакете 

Решение
Определим массу второго пакета. Она на 
Масса второго пакета 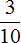
Масса обоих пакетов 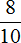
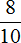


1000 : 2 × 1 = 500 × 1 = 500 г
1000 : 5 × 1 = 200 × 1 = 200 г
Во втором пакете на 200 граммов меньше, поэтому чтобы определить массу второго пакета, нужно из 500 г вычесть 200 г
500 − 200 = 300 г
Ну и напоследок сложить массы обоих пакетов:
500 + 300 = 800 г
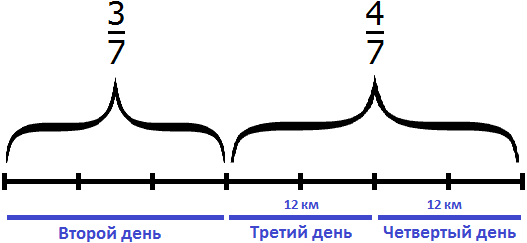
Задача 16. Туристы прошли путь от турбазы до озера за 4 дня. В первый день они прошли 

Решение
В задаче сказано, что во второй день туристы прошли 



В третий и четвертый день туристы прошли 24 км и это составляет 

24 : 4 × 7 = 6 × 7 = 42 км
Во второй, третий и четвертый день туристы прошли 42 км. Теперь найдем 
42 : 7 × 3 = 6 × 3 = 18 км
Теперь возвращаемся к началу задачи. Сказано, что в первый день туристы прошли 
Зная, что пути составляют 42 километра, мы можем найти длину всего пути:
42 : 3 × 4 = 56 км
Значит длина пути от турбазы до озера составляет 56 километров. Сделаем проверку. Для этого сложим все пути, пройденные туристами в каждый из четырех дней.
Сначала найдем путь пройденный в первый день:
56 : 4 × 1 = 14 (в первый день)
14 + 18 + 12 + 12 = 56
Задача из арифметики известного среднеазиатского математика Мухаммеда ибн-Мусы ал-Хорезми (IX век н. э.)
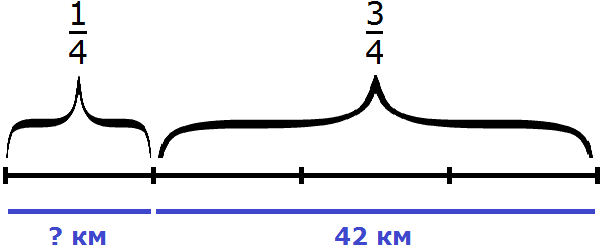
«Найти число, зная, что если отнять от него одну треть и одну четверть, то получится 10»
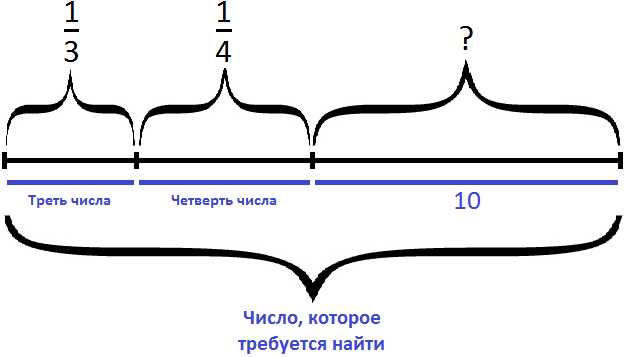
Изобразим число, которое мы хотим найти, в виде отрезка, разделенного на три части. В первой части отрезка отметим треть, во второй — четверть, оставшаяся третья часть будет изображать число 10.
Сложим треть и четверть:
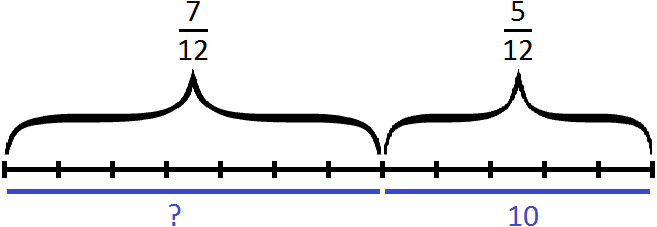
Теперь изобразим отрезок, разделенный на 12 частей. Отметим на нем дробь 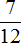
Зная, что пять двенадцатых числа составляют число 10, мы можем найти всё число:
10 : 5 × 12 = 2 × 12 = 24
Мы нашли всё число — оно равно 24.
Эту задачу можно решить не приводя рисунков. Для этого, сначала нужно сложить треть и четверть. Затем из единицы, которая играет роль неизвестного числа, вычесть результат сложения трети и четверти. Затем по полученной дроби определить всё число:
Задача 17. Семья, состоящая из четырех человек, в месяц зарабатывает 80 тысяч рублей. Бюджет распланирован следующим образом: 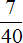


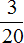
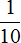
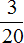
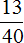
Решение
80 : 40 × 7 = 14 (тыс. на еду)
80 : 20 × 1 = 4 × 1 = 4 тыс. (на коммунальные услуги)
80 : 20 × 1 = 4 × 1 = 4 тыс. (на Интернет и ТВ)
80 : 20 × 3 = 4 × 3 = 12 тыс. (на лечение и походы по врачам)
80 : 10 × 1 = 8 × 1 = 8 тыс. (на пожертвование в детский дом)
80 : 20 × 3 = 4 × 3 = 12 тыс. (на проживание в съемной квартире)
80 : 40 × 13 = 2 × 13 = 26 тыс. (в копилку)
Проверка
14 + 4 + 4 + 12 + 8 + 12 + 26 = 80
Задача 18. Туристы во время похода за первый час прошли 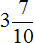
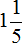
Решение
Найдем числа по дробям. 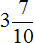
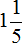
Определим длину пути, пройденного туристами за второй час. Для этого к 3 км 700 м нужно прибавить 1 км 200 м
3 км 700 м + 1 км 200 м = 3700м + 1200м = 4900м = 4 км 900 м
Определим длину пути, пройденного туристами за два часа:
3 км 700 м + 4 км 900 = 3700м + 4900м = 8600м = 8 км 600 м
Значит за два часа туристы прошли 8 километров и еще 600 метров. Решим эту задачу с помощью дробей. Так её можно значительно укоротить
Получили ответ 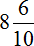
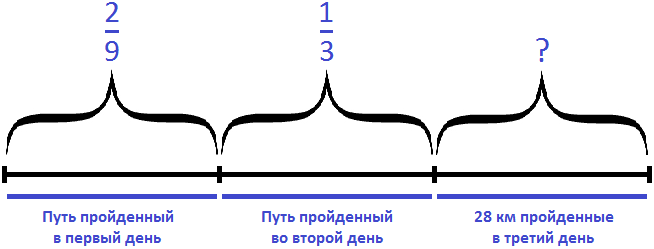
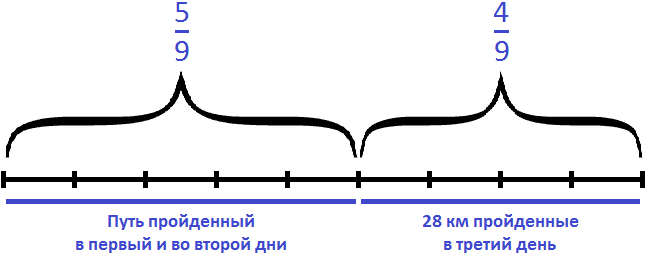
Задача 19. Геологи прошли долину, расположенную между горами, за три дня. В первый день они прошли 

Решение
Изобразим путь в виде отрезка, разделенного на три части. В первой части отметим 

Сложим части пути, пройденные в первый и во второй день:
За первый и второй дни геологи прошли 


28 : 4 × 9 = 7 × 9 = 63 км
Проверка
63 : 9 × 5 = 7 × 5 = 35
63 : 9 × 4 = 7 × 4 = 28
Задача 20. Для приготовления крема использовали сливки, сметану и сахарную пудру. Сметану и сливки составляют 844,76 кг, а сахарная пудра и сливки 739,1 кг. Сколько в отдельности сливок, сметаны и сахарной пудры содержится в 1020,85 кг крема?
Решение
сметана и сливки — 844,76 кг
сахарная пудра и сливки — 739,1 кг
Вытащим из 1020,85 кг крема сметану и сливки (844,76 кг). Так мы найдем массу сахарной пудры:
1020,85 кг — 844,76 кг = 176,09 (кг сахарной пудры)
Вытащим из сахарной пудры и сливок сахарную пудру (176,09 кг). Так мы найдем массу сливок:
739,1 кг — 176,09 кг = 563,01 (кг сливок)
Вытащим сливки из сметаны и сливок. Так мы найдем массу сметаны:
844,76 кг — 563,01 кг = 281,75 (кг сметаны)
176,09 (кг сахарная пудра)
563,01 (кг сливки)
281,75 (кг сметана)
Проверка
176,09 кг + 563,01 кг + 281,75 кг = 1020,85 кг
1020,85 кг = 1020,85 кг
Задача 21. Масса бидона, заполненного молоком равна 34 кг. Масса бидона, заполненного наполовину, равна 17,75 кг. Какова масса пустого бидона?
Решение
Вычтем из массы бидона, заполненного молоком, массу бидона заполненного наполовину. Так мы получим массу содержимого бидона, заполненного наполовину, но уже без учета массы бидона:
34 кг − 17,75 кг = 16,25 кг
16,25 это масса содержимого бидона заполненного наполовину. Умножим эту массу на 2, получим массу бидона заполненного полностью:
16,25 кг × 2 = 32,5 кг
32,5 кг это масса содержимого бидона. Чтобы вычислить массу пустого бидона, нужно из 34 кг вычесть массу его содержимого, то есть 32,5 кг
34 кг − 32,5 кг = 1,5 кг
Ответ: масса пустого бидона составляет 1,5 кг.
Задача 22. Сливки составляют 0,1 массы молока, а сливочное масло составляет 0,3 массы сливок. Сколько сливочного масла можно получить из суточного надоя коровы, равного 15 кг молока?
Решение
Определим сколько килограмм сливок можно получить с 15 кг молока. Для этого найдем 0,1 часть от 15 кг.
15 × 0,1 = 1,5 (кг сливок)
Теперь определим сколько сливочного масла можно получить с 1,5 кг сливок. Для этого найдем 0,3 часть от 1,5 кг
1,5 кг × 0,3 = 0,45 (кг сливочного масла)
Ответ: из 15 кг молока можно получить 0,45 кг сливочного масла.
Задача 23. 100 кг клея для линолеума содержат 55 кг асфальта, 15 кг канифоли, 5 кг олифы и 25 кг бензина. Какую часть этого клея образует каждая из его составляющих?
Решение
Представим, что 100 кг клея как 100 частей. Тогда на 55 частей приходится асфальт, на 15 частей — канифоль, на 5 частей — олифа, на 25 частей — бензин. Запишем эти части в виде дробей, и по возможности сократим получающиеся дроби:
Ответ: 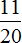
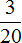


Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Задачи для самостоятельного решения
Решение
Ответ: масса двух пакетов вместе составляет 1 кг 300 г
Решение
Второй способ
Ответ: театральное представление длилось 2 часа 10 минут.
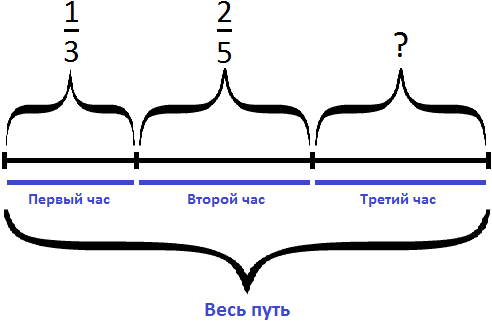
Решение
Определим часть пути, пройденного лыжником за два часа движения. Для этого сложим дроби, выражающие пути пройденные за первый и второй час:
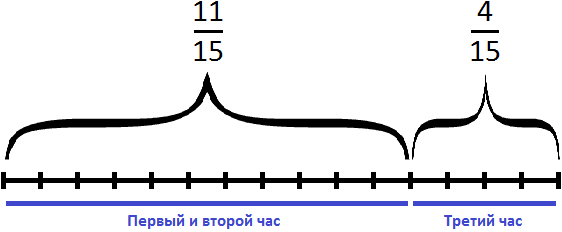
Определим часть пути, пройденного лыжником за третий час. Для этого из всех частей вычтем часть пути, пройденного за первый и второй час движения:
Ответ: в третий час лыжник прошел 
Решение
Определим часть школьников, которые участвовали в футболе, баскетболе и в прыжках:
Определим часть школьников, которые участвовали в беге:
Узнаем на какую часть бегунов больше (или меньше) чем футболистов. Для начала сравним дроби 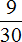
Требовалось узнать на какую часть бегунов больше (или меньше) чем футболистов. Мы выяснили, что бегунов меньше, чем футболистов. Выясним на какую часть их меньше:
Бегунов меньше, чем футболистов на 
Теперь узнаем на какую часть бегунов больше (или меньше) чем баскетболистов. Для начала сравним дроби 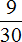
Требовалось узнать на какую часть бегунов больше (или меньше) чем баскетболистов. Мы выяснили, что бегунов больше, чем баскетболистов. Выясним на какую часть их больше:
Бегунов больше, чем баскетболистов на часть.
Ответ: бегунов было на 
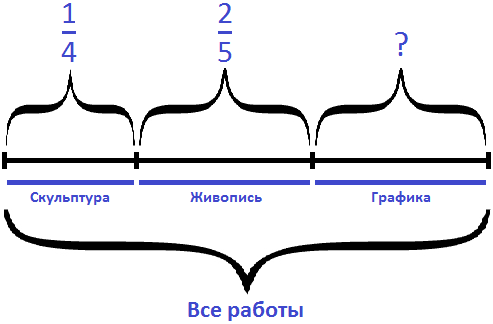
Задача 5. На выставке художественных работ представлена живопись, скульптура и графика. 

Решение
Сложим дроби, выражающие скульптуру и живопись:
Определим какую часть всех работ составляет графика:
Ответ: 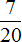
Задача 6. Рабочие отремонтировали дорогу длиной 820 м за три дня. Во вторник они отремонтировали 
Решение
Определим длину дороги, отремонтированной во вторник:
820 : 5 × 2 = 328 м
Определим длину дороги, отремонтированной в среду. Известно, что в этот день рабочие отремонтировали оставшейся дороги. Оставшаяся дорога это 820−328, то есть 492
492 : 3 × 2 = 328 м
Определим длину дороги, отремонтированной в четверг. Для этого вычтем из 820 длины дорог, отремонтированных во вторник и в среду:
820 − (328 + 328) = 820 − 656 = 164 м
Ответ: в четверг рабочие отремонтировали 164 метра дороги.
Задача 7. В книге три рассказа. Наташа прочла первый рассказ за 
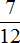
Решение
Определим время за которое Наташа прочитала первый рассказ. Она прочила его за треть часа. Треть часа это 20 минут
60 : 3 × 1 = 20 минут
Определим время за которое Наташа прочитала второй рассказ. Она прочила его на ч больше. часа это 10 минут. Прибавим к 20 минутам 10 минут, получим время чтения второго рассказа:
20 + 10 = 30 минут
Определим время за которое Наташа прочитала третий рассказ. Она прочитала его на 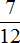
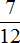
Определим сколько времени ушло у Наташи на чтение всей книги:
20 + 30 + 15 = 65 минут = 1 ч 5 минут
На чтение всей книги у Наташи ушел 1 час и 5 минут. Решим эту задачу с помощью дробей. Так ее можно значительно укоротить:
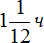

Ответ: на чтение всей книги у Наташи ушло
Задача 8. Из одной тонны хлопка-сырца можно изготовить 3400 м ткани, 1,05 ц пищевого масла и 0,225 т жмыха. Сколько метров ткани, пищевого масла и жмыха можно получить из 32,4 ц хлопка-сырца?
Решение
Переведем 32,4 ц в тонны. Одна тонна составляет 10 центнеров. Чтобы узнать сколько таких десять центнеров (имеется ввиду тонн) в 32,4 центнерах, нужно 32,4 разделить на 10
Определим сколько метров ткани можно получить с 3,24 тонн хлопка-сырца. С одной тонны, как указано в задаче, получается 3400 метров ткани. А с 3,24 тонн будет получено в 3,24 раза больше ткани
3400 × 3,24 = 11016 метров ткани.
Определим сколько пищевого масла можно получить с 3,24 тонн хлопка-сырца. С одной тонны, как указано в задаче, получается 1,05 ц пищевого масла. А с 3,24 тонн будет получено в 3,24 раза больше масла
1,05 × 3,24 = 3,402 центнера пищевого масла
Определим сколько жмыха можно получить с 3,24 тонн хлопка-сырца. С одной тонны, как указано в задаче, получается 0,225 т жмыха. А с 3,24 тонн будет получено в 3,24 раза больше жмыха
0,225 × 3,24 = 0,729 тонн жмыха
Ответ: из 32,4 ц хлопка сырца можно получить 11016 метров ткани, 3,402 ц пищевого масла и 0,729 т жмыха.
Решение
Зная, что 0,2 всего пути составляют 12 км, мы можем найти весь путь. Чтобы найти неизвестное число по десятичной дроби, нужно известное число разделить на десятичную дробь
Ответ: Туристы прошли 60 км.
Решение
Зная, что 0,7 книги составляют 56 страниц, мы можем узнать сколько всего страниц в книге. Чтобы найти неизвестное число по десятичной дроби, нужно известное число разделить на десятичную дробь
56 : 0,7 = 80 (страниц всего)
Узнаем сколько осталось прочитать
80 − 56 = 24 (страницы осталось прочитать)
Ответ: в книге 80 страниц. Прочитать осталось еще 24 страницы.
Решение
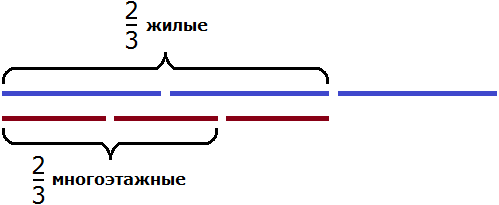
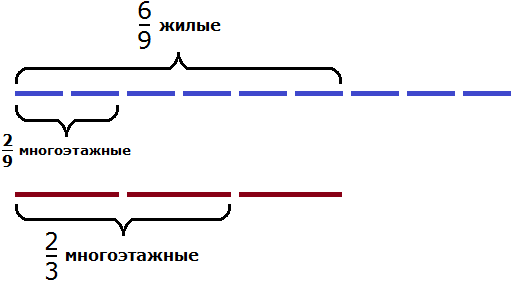
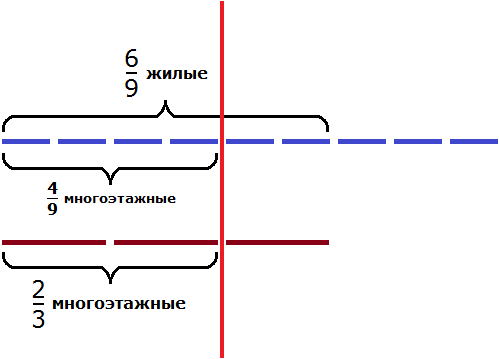
Разделим жилых домов на три части:
Теперь на треть многоэтажных домов приходится 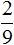
Чтобы узнать сколько многоэтажных домов приходится на две трети, умножим 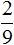
Ответ: жилые многоэтажные дома составляют 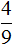
Решение
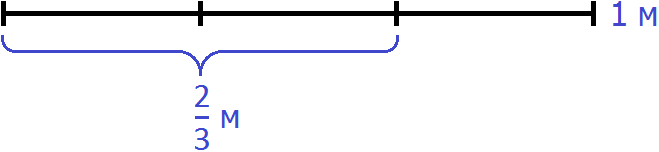
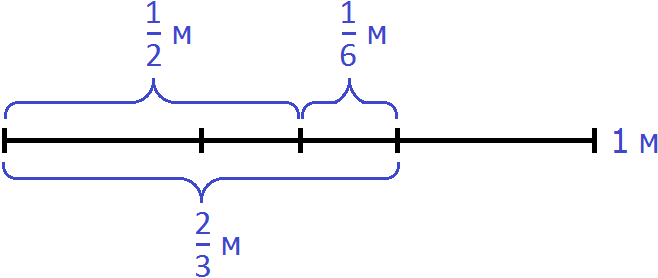
Изобразим схематически один метр веревки:
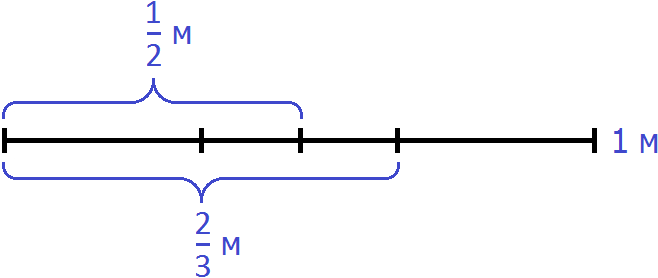
Выделим на этом рисунке метра:
Здесь же выделим 
Не выделенным на м остался один кусочек. Узнаем, что это за кусочек. Для этого из вычтем
м это часть веревки, которую нужно отрезать. Тогда мы получим 
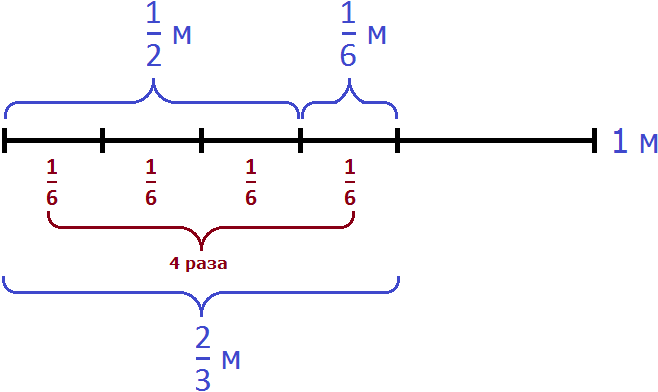
Теперь осталось узнать сколько раз м содержит м
Значит, чтобы не производя измерений от м веревки отрезать 
Ответ: чтобы от веревки, длина которой м отрезать 

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Видео:Виленкин. 6 класс за 100 минут. Математика: теория чисел, дроби, уравненияСкачать

30 thoughts on “Задачи на дроби”
Здравствуйте! Очень благодарна вам за ваши труды. Очень все доступно объясняете.
В задаче №2 есть опечатка. В условии одна целая пять шестых часа, а в решении одна целая две трети.
Добавлю, что задача №2 в разделе самостоятельного решения.
Здравствуйте! Спасибо вам большое за задачи!
Но я никак не могу понять, почему в 16 задаче такое решение. Почему 3/7 оставшегося пути не вычисляются из 24км? Ведь второй день = 3/7 оставшегося пути, этот путь равен 24км. Он не может включать и второй день? Разве нет?
24 км это путь, пройденный в третий и четвертый дни. А во второй день было пройдено совсем другое расстояние.
Вообще, во второй, третий и четвертый дни всего было пройдено 42 км.
Найдите от 42 км сначала 3/7 пути, а потом 4/7 пути. Сразу станет всё понятно 😉
А откуда в 3-й задаче взялась дробь 15 на 15?
🔍 Видео
Математика 6 класс (Урок№52 - Решение задач с помощью уравнений. Часть 2.)Скачать

РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ // МАТЕМАТИКА 6 КЛАСССкачать

Математика 6 класс. Решаем задачи с дробями при помощи рисункаСкачать

Решение задач с помощью уравненийСкачать

Решение задач с помощью уравнений. Алгебра 7 классСкачать

Решение задач с помощью уравнений.Скачать

Решение уравнений ( подобные слагаемые ) . 6 класс .Скачать

Решение уравнений, 6 классСкачать

Решение задач с помощью рациональных уравнений. Алгебра, 8 классСкачать

Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать