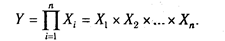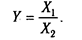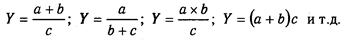Сущность моделирования заключается в том, что взаимосвязь исследуемого показателя с факторными передается в форме конкретного математического выражения.
В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.
1. Аддитивные модели:
Они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.
2. Мультипликативные модели:
Этот тип моделей применяется тогда, когда результативный показатель представляет собой произведение нескольких факторов.
Они применяются тогда, когда результативный показатель получают делением одного факторного показателя на величину другого.
4.Смешанные (комбинированные) модели — это сочетание в различных комбинациях предыдущих моделей:
Возможность использования основных способов детерминированного анализа представлена в таблице 1.
Матица применения способов детерминированного факторного анализа
| Способы | Модели | |||
| Мультипликативная | Аддитивная | Кратная | Смешанная | |
| Цепных подстановок | + | + | + | + |
| Абсолютных разниц | + | — | — | Y=(a-b)c, Y=a(b-c) |
| Относительных (процентных) разниц | + | — | — | — |
| Интегральный | + | — | + | Y=a/Σbi |
Способы измерения факторов
Элиминировать – устранять (исключать) воздействие на результат всех факторов кроме одного.
При этом, исходя из того, что все факторы изменяются независимо друг от друга, сначала изменяют один фактор, а все остальные оставляют без изменения. Потом изменяют два фактора при неизменности остальных и т.д.
Методы элиминирования:
1) Цепных подстановок
2) Абсолютных и относительных разниц
3) Индексный метод
4) Пропорционального деления (долевого участия)
5) Пропорциональных разностей
Способ цепных подстановок используется для расчета влияния факторов во всех типах детерминированных факторных моделей – аддитивных, мультипликативных, кратных, смешанных.
Способ цепных подстановок используется для того, чтобы выявить, какие факторы влияли на анализируемый показатель и из всех действующих факторов выделить основные, имеющие решающее влияние на изменение показателя.
Сущность способа — определяя действие одного фактора, другие факторы принимать как неизменные. Для этого в расчетах последовательно заменяют частные плановые (базовые) показатели отчетными (фактическими). Полученные результаты сравнивают с имеющимися предыдущими данными. Разность показывает размер влияния данного фактора на изменение совокупного показателя.
В общем виде применение способа цепных постановок можно описать следующим образом:
где a0, b0, c0 — базисные значения факторов, оказывающих влияние на обобщающий показатель у;
a1 , b1, c1 — фактические значения факторов;
ya, yb, — промежуточные (условные) изменения результирующего показателя, связанного с изменением факторов а, b, соответственно.
Общее изменение Δу = у1 – у0 складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов:
Δy = Δya + Δyb + Δyc;
Несмотря на универсальность применения и простоту расчетов способ цепных подстановок имеет следующий недостаток: в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения.
На практике точностью оценки факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора.
Правила, определяющие последовательность подстановки:
1) при наличии в факторной модели количественных и качественных показателей в первую очередь рассматривается влияние количественных факторов;
2) если модель представлена несколькими количественными и качественными показателями, то сначала рассматривается влияние факторов первого уровня подчинения, а затем более низкого.
Способ абсолютных разниц (абсолютных отклонений) – это модификация способа цепных подстановок. Он прост в расчетах, но менее универсален – с его помощью производят расчет влияния факторов только для мультипликативных моделей и моделей смешанного типа:
Для мультипликативной модели расчет производится умножением абсолютного прироста исследуемого фактора на базисную величину факторов, находящихся справа от него, и на фактическую величину факторов, расположенных в модели слева от него.
В общем виде применение способа абсолютных разниц можно описать следующим образом:
Δya = Δa * b0 * c0;
где a0, b0, c0 — базисные значения факторов, оказывающих влияние на обобщающий показатель у;
a1 , b1, c1 — фактические значения факторов;
Δa=a1-a0, Δb=b1-b0, Δc=c1-c0, — абсолютные изменения (отклонение факта от базы или плана) факторов а, b, с соответственно.
Общее изменение Δу = у1 – у0 складывается из суммы изменений результирующего показателя за счет изменения каждого фактора:
Δy = Δya + Δyb + Δyc.
Способ относительных (процентных) разниц применяется для измерения влияния факторов на прирост результативного показателя только в тех моделях, где взаимодействие факторов выражено произведением, т.е. в мультипликативных моделях.
Здесь используются относительные приросты факторных показателей, выраженные в виде коэффициентов или процентов.
Для мультипликативных моделей типа у = а*в*с
методика анализа следующая.
Находят относительное отклонение каждого факторного показателя:
Δа% = ((а1-а0)/а0)*100%;
Определяют отклонение результативного показателя за счет каждого фактора:
Δув = ((у0+ Δуа)*Δв%)/100;
Δус = ((у0+Δуа+ Δув)*Δс%)/100;
где a0, b0, c0 – базисные (плановые) значения факторов, оказывающих влияние на результативный показатель;
a1 , b1, c1 — фактические значения факторов;
Общее изменение Δу = у1 – у0 складывается из суммы изменений результативного показателя за счет изменения каждого фактора:
Δy = Δya + Δyb + Δyc.
В способе относительных разниц используется прием нарастающего итога. Расчет влияния первого фактора производят умножением базисной величины результативного показателя на относительный прирост первого фактора, выраженного либо в виде дроби, либо в виде процентов.
Чтобы рассчитать влияние второго фактора, нужно к базисной величине результативного показателя прибавить его изменение за счет первого фактора и полученную сумму умножить на относительный прирост второго фактора.
Влияние третьего фактора определяется аналогично: к базисной величине результативного показателя прибавляют его прирост за счет первого и второго факторов и результат умножают на относительный прирост третьего фактора и т.д.
Не смотря на ограниченность использования этого способа, у него есть следующее преимущество: способ относительных разниц удобно применять тогда, когда требуется рассчитать влияние большого числа факторов (8-10 и более). При этом значительно сокращается количество вычислительных процедур.
Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер – применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях.
Использование этого способа позволяет получить более точные результаты по сравнению с остальными выше названными способами, поскольку дополнительный прирост результативного показателя от взаимодействия факторов присоединяется не к последнему фактору, а делится поровну между ними.
Алгоритмы расчетов влияния факторов для различных моделей, приводимые в специальной литературе:
Мультипликативная модель вида f = x*y:
Δf(x) = Δx*y0 + ½Δx*Δy, или Δf(x) = ½Δx (y0 + y1);
Δf(y) = Δy*x0 + ½Δx*Δy, или Δf(y) = ½Δy (x0 + x1);
где x0, y0 – базисные (плановые) значения факторов, оказывающих влияние на результативный показатель;
x1, y1 — фактические значения факторов;
Δx = x1-x0, Δy = y1-y0 — абсолютные изменения (отклонения) факторов х, у соответственно;
Мультипликативная модель вида f = x*y*z:
Δf(x) = ½Δx (y0*z1 + y1*z0) + ⅓Δx*Δy*Δz;
Δf(y) = ½Δy (x0*z1 + x1*z0) + ⅓Δx*Δy*Δz;
Δf(z) = ½Δz (x0*y1 + x1*y0) + ⅓Δx*Δy*Δz;
Кратная модель вида f = x/y:
Δf(x) = Δx/Δy * ln |y1/y0|;
Δf(y) = Δf — Δf(x) = (f1-f0) — Δf(x);
Смешанная модель вида f = x/(y+z):
Δf(x) = Δx/(Δy+Δz) * ln |(y1+z1)/(y0+z0)|;
Δf(y) = (Δf — Δf(x))Δy / (Δy+Δz);
Δf(z) = (Δf — Δf(x))Δz / (Δy+Δz).
ТРЕТИЙ УЧЕБНЫЙ ВОПРОС
Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам.
Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот.
ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.
Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Видео:УРАВНЕНИЕ ПО МОДУЛЮ 😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Математическое уравнение отражающее взаимосвязь результативного показателя с несколькими факторными показателями, относится к типу . факторных моделей.
29. К экономико-математическим методам анализа относится:
1. метод исследования операций;
30. Определить соответствие индивидуальных затрат на предприятии общественно необходимым, его организационно-технический уровень и место в ряду предприятий аналогичной производственной специализации позволяет:
3. сравнение со среднеотраслевыми данными
31. Метод ………. заключается в получении ряда промежуточных значений результативного
показателя путем последовательной замены базисных (плановых) значений факторов на
Фактические, с последующим сравнением величины результативного показателя до и после изменения
32. Математическое уравнение У =(a+b) / c, отражающие взаимосвязь результативного показателя с несколькими факторными показателями, относится к типу ________ факторных моделей.
Анализ предполагает определение структуры итоговых показателей бухгалтерской отчетности с выявлением влияния каждой позиции на результат в целом
34. Горизонтальный (временной) метод финансового анализа предполагает:
3. сравнение каждой позиции отчетности с предыдущим периодом с выявлением абсолютных и относительных отклонений;
35. При использовании метода ________величина влияния факторов рассчитывается
умножением абсолютного прироста значения исследуемого фактора на базисную (плановую) величину
Факторов, которые в модели находятся справа от него, и на фактическую величину факт
36. . — это относительные показатели сравнения явлений, состоящих из элементов, непосредственно не поддающихся суммированию:
37. Математическое уравнение Y=X1/X2, отражающее взаимосвязь результативного
показателя с несколькими факторными показателями, относится к типу __________ факторных
Моделей.
38. ________ Методы экономического анализа хозяйственной деятельности основаны на использовании профессиональных знаний, опыта и интуиции аналитика:
1. эвристические (экспертные)
Для выявления причин отклонения фактических значений отдельных показателей от их
прогнозируемых уровней применяется сравнение:
1. отчетных показателей с плановыми показателями
Метод анализа, при котором исключается действие ряда факторов на результативный
показатель и выделяется один из них, называется:
41. Метод анализа, предполагающий сопоставление однородных объектов для нахождения черт сходства или различий между ними, называется:
42. К экономико-математическим методам анализа относится:
1. вариационное исчисление
43. Оценка динамики финансовых показателей проводится с помощью метода:
2. горизонтального анализа
Расчет относительных показателей по данным бухгалтерской отчетности, отражающих
Внутрибалансовые взаимосвязи между показателями нескольких форм отчетности, проводится на
2. финансовых коэффициентов
45. Математическое уравнениеY=(a+b)*c, отражающее взаимосвязь результативного
показателя с несколькими факторными показателями, относится к типу ________ факторных моделей:
4. смешанных (комбинированных).
Величина выражает собой отличительную особенность данной совокупности
Явлений, устанавливает наиболее типичные черты этой совокупности.
Анализ изучает влияние исходных величин на результативный показатель с помощью детерминированных приемов исследования
Для выявления тенденций развития предприятия и динамики основных параметров его
экономического и финансового положения используется:
2. сравнение отчетных показателей с показателями предшествующих периодов;
49. К экономико-математическим методам анализа не относятся методы:
50. Оценка динамики финансовых показателей проводится с помощью метода:
2. горизонтального анализа
Расчет относительных показателей по данным бухгалтерской отчетности, отражающих
Внутрибалансовые взаимосвязи между показателями нескольких форм отчетности, проводится на
основе метода:
2. финансовых коэффициентов
52. Математическое уравнениеY=(a+b)*c, отражающее взаимосвязь результативного
показателя с несколькими факторными показателями, относится к типу ________ факторных моделей:
4. смешанных (комбинированных)
Величина выражает собой отличительную особенность данной совокупности явлений, устанавливает наиболее типичные черты этой совокупности.
Анализ изучает влияние исходных величин на результативный показатель с помощью детерминированных приемов исследования
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Перечислите задачи экономического анализа.
В чем состоит взаимосвязь управленческого учета и экономического анализа?
Экономический анализ выступает не только важнейшей составляющей любой из функций управления, но и сам является видом управленческой деятельности, предшествующей принятию управленческих решений, направленных на устойчивое развитие бизнеса организации. Таким образом, экономический анализ занимает промежуточное место между подбором информации и процессом принятия решений и в зависимости от характера принимаемого решения использует соответствующие методы
Что является предметом и объектами экономического анализа?
Предметом экономического анализа являются причины изменения результатов хозяйствования и их отклонений от целевых параметров. Познание причинно-следственных связей в хозяйственной деятельности предприятий позволяет раскрыть сущность происходящих в ней процессов и на этой основе дать правильную оценку достигнутым результатам в сложившейся ситуации, выявить резервы повышения эффективности работы, обосновать планы и управленческие решения, направленные на достижение поставленных целей.
Перечислите задачи экономического анализа.
1.Установление закономерностей и тенденций изменения экономических показателей в конкретных условиях предприятия.
2. Оценка результатов деятельности предприятия на основе объективного и всестороннего изучения учетной и отчетной информации.
3. Научное обоснование текущих и перспективных планов развития предприятия
4. Контроль выполнения плановых заданий и использования производственных ресурсов.
5. Выявление и измерение внутренних резервов эффективности функционирования предприятия на всех стадиях производственного процесса.
6. Разработка мероприятий по использованию резервов производства.
7. Принятие оптимальных управленческих решений по совершенствованию деятельности предприятия.
4.Каково содержание анализа и диагностики хозяйственной деятельности? Содержание анализа финансово-хозяйственной деятельности состоит во всестороннем изучении технического уровня производства, качества и конкурентоспособности выпускаемой продукции, обеспеченности производства материалами, трудовыми и финансовыми ресурсами и эффективности их использования. Этот анализ основан на системном подходе, комплексном учете разнообразных факторов, качественном подборе достоверной информации и является важной функцией управления.
Сущность диагностики финансово-хозяйственной деятельности предприятия состоит в установлении и изучении признаков, измерении основных характеристик, отражающих состояние машин, приборов, технических систем, экономики и финансов хозяйствующего субъекта, для предсказания возможных отклонений от устойчивых, средних, стандартных значений и предотвращения нарушений нормального режима работы
5.Дайте характеристику взаимосвязи основных экономических показателей как базы комплексного анализа.
объекты, цель и задачи анализа, составляется план аналитической работы; разрабатывается система синтетических и аналитических показателей, с помощью которых
характеризуется объект анализа;
собирается и подготавливается к анализу необходимая информация;
проводится сравнение фактических результатов хозяйствования с показателями плана отчетного года, фактическими данными прошлых лет, с достижениями ведущих предприятий, отрасли и т.д.;
факторный анализ: выделяются факторы и определяется их влияние на результат;
выявляются неиспользованные и перспективные резервы повышения эффективности производства; оценка результатов хозяйствования с учетом действия различных факторов и выявленных
неиспользованных резервов, разрабатываются мероприятия по их использованию.
6. Перечислите задачи аналитических исследований по темам комплексного экономического анализа хозяйственной деятельности. Общие:
1. Оценка качества, обоснованности и достоверности планов и нормативов.
2. Определение базовых показателей для планирования на предстоящий период.
3. Контроль за выполнением планов и оценка их выполнения. Здесь же дается оценка эффективности использования материальных, трудовых и финансовых ресурсов.
4. Определение влияния отдельных факторов и их количественная оценка. Выделение и измерение влияния внутренних (зависящих от деятельности предприятия) и внешних (отраслевых) факторов.
5. Выявление резервов роста эффективности производства.
6. Обоснование управленческих решений и их оптимизация.
7. объективная оценка финансового состояния хозяйствующего субъекта, его платежеспособности, финансовой устойчивости и деловой активности.
8.выявление возможностей увеличения собственного капитала, чистых активов, доходности акций и улучшения использования заемных средств.
9.прогнозирование финансовых результатов, потенциальной угрозы банкротства.
Специфические:
• выбор партнеров по публикуемой о них информации;
• оценка и проверка (due diligence) приобретаемой организации (бизнеса);
• совершенствование методики экономического анализа с учетом международного опыта и перестройкой бухгалтерского учета и отчетности по международным стандартам;
• разработка приемов анализа эффективности вложения финансовых ресурсов в реальное и портфельное инвестирование;
• совершенствование методик по анализу качества, надежности продукции, ее конкурентоспособности на внутреннем и внешнем рынке;
• анализ капитализации организации и потенциала роста бизнеса;
• разработка методик социального, регионального анализа, природоохранной деятельности;
• анализ эффективности внедрения аутсорсинга;
• развитие нетрадиционных видов анализа: непрерывного, многовариантного, стратегического, диагностического.
Выполнить тест
1. Основополагающие принципы метода экономического анализа не отражает следующая черта диалектики:
а) единство анализа и синтеза;
б) изучение экономических явлений в их взаимосвязи;
в) изучение экономических явлений в развитии, в динамике;
г) единство и борьба противоположностей.
2. Математическое уравнение У = 
3. К экономико-математическим методам анализа относится:
а) метод исследования операций:
б) трендовый анализ;
в) коэффициентный анализ;
г) горизонтальный анализ.
4. К классу кратных детерминированных факторных моделей не применяется способ их преобразования (моделирования):
а) удлинения факторной системы;
б) расширения факторной системы;
в) сокращения факторной системы;
г) раздвоения факторной системы.
5. Определить соответствие индивидуальных затрат на предприятии общественно необходимым, его организационно-технический уровень и место в ряду предприятий аналогичной производственной специализации позволяет:
а) сравнение отчетных показателей с показателями предшествующих периодов;
б) межхозяйственное сравнение;
в) сравнение со среднеотраслевыми данными;
г) сравнение показателей предприятия со средними показателями рыночной экономики.
6. Метод цепных подстановок. заключается в получении ряда промежуточных значений результативного показателя путем последовательной замены базисных (плановых) значений факторов на фактические, с последующим сравнением величины результативного показателя до и после изменения уровня исследуемого фактора.
7. Математическое уравнение У = 
8. ..Вертикальный. анализ предполагает определение структуры итоговых показателей бухгалтерской отчетности с выявлением влияния каждой позиции на результат в целом.
9. Горизонтальный (временной) метод финансового анализа предполагает:
а) определение структуры итоговых показателей бухгалтерской отчетности с выявлением влияния каждой позиции на результат;
б) выявление основной тенденции динамики показателя, очищенной от случайных влияний и особенностей отдельных периодов;
в) сравнение каждой позиции отчетности с предыдущим периодом с выявлением абсолютных и относительных отклонений;
г) сравнение показателей фирмы с показателями фирм-конкурентов, со среднеотраслевыми и общеэкономическими показателями.
10. При использовании метода . абсолютных разниц.. величина влияния факторов рассчитывается умножением абсолютного прироста значения исследуемого фактора на базисную (плановую) величину факторов, которые в модели находятся справа от него, и на фактическую величину факторов, расположенных в модели слева от него.
11. Интегральный….. метод основан на суммировании приращений функции, определенной как частная производная, умноженная на приращение аргумента на бесконечно малых промежутках.
12. .Индексный анализ.. — это относительные показатели сравнения явлений, состоящих из элементов, непосредственно не поддающихся суммированию:
б) финансовые коэффициенты:
г) средние величины.
13. Математическое уравнение У = 
14. . методы экономического анализа хозяйственной деятельности основаны на использовании профессиональных знаний, опыта и интуиции аналитика:
а) эвристические;
15. Метод комплексной оценки эффективности хозяйственной деятельности, предполагающий присвоение каждому показателю и его приращению весового коэффициента по определенной шкале, называется методом:
б) балльной оценки;
в) прироста совокупного ресурса;
г) финансовых коэффициентов.
16. Метод, предполагающий сравнение каждой позиции отчетности с рядом предшествующих периодов и определение основной тенденции динамики показателя, очищенной от случайных влияний и особенностей отдельных периодов, называется . горизонтальным (временным) .. анализом.
17. Для выявления причин отклонения фактических значений отдельных показателей от их прогнозируемых уровней применяется сравнение:
а) отчетных показателей с плановыми показателями;
б) отчетных показателей с показателями предшествующих периодов;
в) показателей предприятия с аналогичными среднеотраслевыми данными;
г) показателей предприятия со средними показателями рыночной экономики.
18. Метод анализа, при котором исключается действие ряда факторов на результативный показатель и выделяется один из них, называется:
а) рядами динамики;
б) элиминированием;
г) балансовыми увязками.
19. Метод анализа, предполагающий сопоставление однородных объектов для нахождения черт сходства или различий между ними, называется:
в) выборочным и сплошным наблюдением;
г) сравнением.
20. К экономико-математическим методам анализа относится:
а) вариационное исчисление;
б) трендовый анализ;
в) факторный анализ;
г) вертикальный анализ.
21. Оценка динамики финансовых показателей проводится с помощью метода:
а) вертикального анализа;
б) горизонтального анализа;
в) финансовых коэффициентов;
г) сравнительного анализа.
22. Расчет относительных показателей по данным бухгалтерской отчетности, отражающих внутрибалансовые взаимосвязи или взаимосвязи между показателями нескольких форм отчетности, проводится на основе метода:
а) экономико-математического анализа;
б) финансовых коэффициентов;
в) сравнительного (пространственного) анализа;
г) факторного анализа.
23. Математическое уравнение У=(а+b)/с, отражающее взаимосвязь результативного показателя с несколькими факторными показателями, относится к типу . факторных моделей:
г) смешанных (комбинированных).
24. Средняя. величина выражает собой отличительную особенность данной совокупности явлений, устанавливает наиболее типичные черты этой совокупности.
25. факторный. анализ изучает влияние исходных величин на результативный показатель с помощью детерминированных приемов исследования.
26. Для выявления тенденций развития предприятия и динамики основных параметров его экономического и финансового положения используется:
а) сравнение отчетных показателей с плановыми показателями;
б) сравнение отчетных показателей с показателями предшествующих периодов;
в) межхозяйственное сравнение;
г) сравнение со среднеотраслевыми данными.
27. К экономико-математическим методам анализа не относятся методы:
а) элементарной математики;
3) б) математического программирования;
в) исследования операций;
г) элиминирования.
28. Математическое уравнение У = 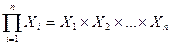
29. Методы . позволяют дать комплексную оценку финансового состояния предприятия:
а) математической статистики;
б) определения рейтинговой оценки;
в) детерминированного факторного анализа;
г) математического программирования.
30. К стандартным приемам (методам) анализа бухгалтерской отчетности относится . анализ:
в) горизонтальный;
Не нашли, что искали? Воспользуйтесь поиском:
Видео:7 класс, 3 урок, Что такое математическая модельСкачать

Виды математических моделей
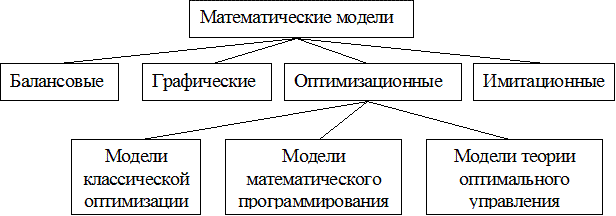
В зависимости от того, какими средствами, при каких условиях и по отношению к каким объектам познания реализуется способность моделей отображать действительность, возникает их большое разнообразие, а вместе с ним — классификации. Путем обобщения существующих классификаций выделим базовые модели по применяемому математическому аппарату, на основе которых получают развитие специальные модели (рисунок 8.1).
Рисунок 8.1 — Формальная классификация моделей
Математические модели отображают изучаемые объекты (процессы, системы) в виде явных функциональных соотношений: алгебраических равенств и неравенств, интегральных и дифференциальных, конечно-разностных и других математических выражений (закон распределения случайной величины, регрессионные модели и т.д.), а также отношений математической логики.
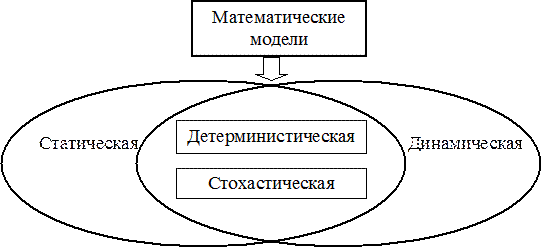
В зависимости от двух фундаментальных признаков построения математической модели — вида описания причинно-следственных связей и изменений их во времени — различают детерминистические и стохастические, статические и динамические модели (рисунок 8.2).
Цель схемы, представленной на рисунке, — отобразить следующие особенности:
1) математические модели могут быть и детерминистическими, и стохастическими;
2) детерминистические и стохастические модели могут быть и статическими, и динамическими.
Математическая модель называется детерминистической (детерминированной), если все ее параметры и переменные являются однозначно определяемыми величинами, а также выполняется условие полной определенности ин 
Рисунок 8.2 – Классы математических моделей
Модель называется динамической, если как минимум одна переменная изменяется по периодам времени, и статической, если принимается гипотеза, что переменные не изменяются по периодам времени.
В простейшем случае балансовые модели выступают в виде уравнения баланса, где в левой части располагается сумма каких-либо поступлений, а в правой — расходная часть также в виде суммы. Например, в таком виде представляется годовой бюджет организации.
На основе статистических данных могут строиться не только балансовые, но и корреляционно-регрессионные модели.
Если функция Y зависит не только от переменных х1, , х2, … хn , но и от других факторов, связь между Y и х1, , х2, … хn является неточной или корреляционной в отличие от точной или функциональной связи. Корреляционными, например, в большинстве случаев являются связи, наблюдающиеся между выходными параметрами ОПС и факторами ее внутренней и внешней среды (см. тему 5).
Корреляционно-регрессионные модели получают при исследовании влияния целого комплекса факторов на величину того или иного признака путем применения статистического аппарата. При этом ставится задача не только установить корреляционную связь, но и выразить эту связь аналитически, то есть подобрать уравнения, описывающие данную корреляционную зависимость (уравнение регрессии).
Для нахождения численного значения параметров уравнения регрессии пользуются методом наименьших квадратов. Суть этого метода состоит в том, чтобы выбрать такую линию, при которой сумма квадратов отклонений от нее ординат Y отдельных точек была бы наименьшей.
Корреляционно-регрессионные модели часто используются при исследовании явлений, когда возникает необходимость установить зависимость между соответствующими характеристиками в двух и более рядах. При этом преимущественно используется парная и множественная линейная регрессия вида
В результате применения метода наименьших квадратов устанавливаются значения параметров a или a1, a2, …, an и b, а затем выполняются оценки точности аппроксимации и значимости полученного уравнения регрессии.
В особую группу выделяют графоаналитические модели. Они используют различные графические изображения и поэтому обладают хорошей наглядностью.
Теория графов — одна из теорий дискретной математики, изучает графы, под которыми понимается совокупность точек и линий их соединяющих. Граф — это самостоятельный математический объект (впервые ввел Кёниг Д.). На основе теории графов наиболее часто строят древовидные и сетевые модели.
Древовидная модель (дерево) — это неориентированный связный граф, не содержащий петель и циклов. Примером такой модели является дерево целей.
Сетевые модели нашли широкое применение в управлении производством работ. Сетевые модели (графики) отражают последовательность выполнения работ и продолжительность каждой работы (рисунок 8.3).
Рисунок 8.3 — Сетевая модель производства работ
Каждая линия сетевого графика — это некоторая работа. Цифра рядом с ней означает продолжительность ее выполнения.
Сетевые модели позволяют найти так называемый критический путь и оптимизировать график производства работ по времени при ограничениях на другие ресурсы.
Сетевые модели могут быть детерминированными и стохастическими. В последнем случае продолжительности выполнения работ задаются законами распределения случайных величин.
Оптимизационные модели служат для определения оптимальной траектории достижения системой поставленной цели при наложении некоторых ограничений на управление ее поведениям и движением. В этом случае оптимизационные модели описывают различного рода задачи нахождения экстремума некоторой целевой функции (критерия оптимизации).
Для выявления оптимального способа достижения цели управления в условиях ограниченных ресурсов – технических, материальных, трудовых и финансовых – применяют методы исследования операций. К ним относятся методы математического программирования (линейное и нелинейное, целочисленное, динамическое и стохастическое программирование), аналитические и вероятностно-статистические методы, сетевые методы, методы теории массового обслуживания, теории игр (теории конфликтных ситуаций) и др.
Оптимизационные модели применяются для объемного и календарного планирования, управления запасами, распределения ресурсов и работ, замены, параметризации и стандартизации оборудования, распределения потоков товарных поставок на транспортной сети и других задач управления.
Одним из основных достижений теории исследования операций считается типизация моделей управления и методов решения задач. Например, для решения транспортной задачи, в зависимости от ее размерности, разработаны типовые методы — метод Фогеля, метод потенциалов, симплекс-метод. Также при решении задачи управления запасами, в зависимости от ее постановки, могут использоваться аналитические и вероятностно-статистические методы, методы динамического и стохастического программирования.
В управлении особое значение придается сетевым методам планирования. Эти методы позволили найти новый и весьма удобный язык для описания, моделирования и анализа сложных многоэтапных работ и проектов. В исследовании операций значительное место отводится совершенствованию управления сложными системами с применением методов теории массового обслуживания (см. раздел8.3) и аппарата марковских процессов.
Модели марковских случайных процессов — система дифференциальных уравнений, описывающих функционирование системы или ее процессов в виде множества упорядоченных состояний на некоторой траектории поведения системы. Этот класс моделей широко используется при математическом моделировании функционирования сложных систем.
Модели теории игр служат для выбора оптимальной стратегии в условиях ограниченной случайной информации или полной неопределенности.
Игра — математическая модель реальной конфликтной ситуации, разрешение которой ведется по определенным правилам, алгоритмам, описывающим некоторую стратегию поведения лица, принимающего решение в условиях неопределенности.
Различают «игры с природой» и «игры с противником». Исходя из ситуации определяются методы и критерии оценки принятия решений. Так, при «играх с природой» применяют критерии: Лапласа, максиминный (критерий Вальда) и минимаксный, Гурвица и Сэвиджа и ряд других алгоритмических правил. При «играх с противником» для принятия решений используются платежные матрицы, максиминный и минимаксный критерии, а также специальные математические преобразования в связи с тем, что лицу, принимающему решение, противостоит недоброжелательный противник.
Рассмотренные типы математических моделей не охватывают всего их возможного многообразия, а лишь характеризуют отдельные виды в зависимости от принятого аспекта классификации. В.А.Кардашем была предпринята попытка создания системы классификации моделей по четырем аспектам детализации (рисунок 8.4).
| Временной аспект | |||
| статические | динамические | ||
| Социальный, организационный, технологический аспекты | Однокритериальные модели | Детерминированные | Стохастический аспект |
| Стохастические | |||
| Модели, учитывающие взаимодействие интересов | Детерминированные | ||
| Стохастические | |||
| А | В | А | В |
| Пространственный аспект |
А — модели без пространственной дифференциации параметров;
В — модели с пространственной дифференциацией параметров
Рисунок 8.4 — Классификация моделей по четырем аспектам детализации
С развитием вычислительных средств одним из распространенных методов принятия решений выступает деловая игра, представляющая собой численный эксперимент с активным участием человека. Существуют сотни деловых игр. Они применяются для изучения целого ряда проблем управления, экономики, теории организации, психологии, финансов и торговли.
Дата добавления: 2014-12-27 ; просмотров: 20814 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
📽️ Видео
1 Как решать уравнения всех видов Решите уравнение Виды уравнений МАТЕМАТИКА ОНЛАЙНСкачать

Как решают уравнения в России и СШАСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Уравнение с модулемСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Страшное уравнение пятой степениСкачать

РЕШЕНИЕ УРАВНЕНИЯ 😉 ЧАСТЬ II #егэ #математика #профильныйегэ #shorts #огэСкачать

Рациональные уравнения как математические модели реальных ситуаций - алгебра 8 классСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Дробно-рациональные уравнения. 8 класс.Скачать

Рациональные уравнения как математические модели реальных ситуаций (урок 1)Скачать

КУБИЧЕСКИЕ УРАВНЕНИЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

ЕГЭ-ПРОФИЛЬ. Номер 1. ВСЕ виды уравнений на ЕГЭСкачать

9 класс, 14 урок, Системы уравнений как математические модели реальных ситуацийСкачать