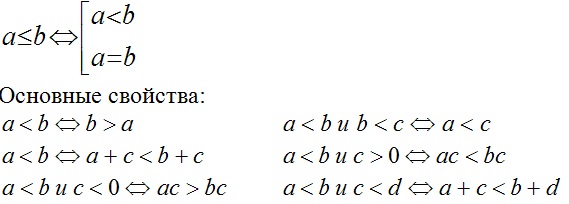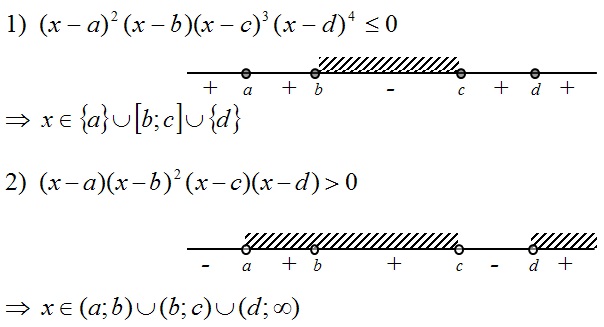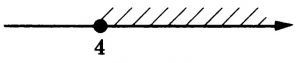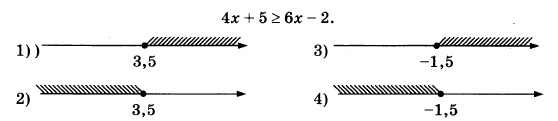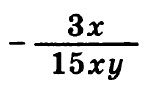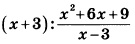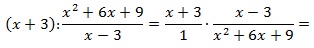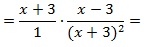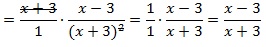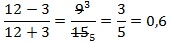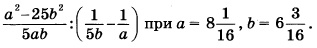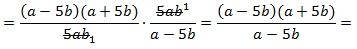В задании №13 проверяется умение решать уравнения, неравенства и их системы. Конечно, под такие слова подходит огромный спектр заданий. Уточнение, пожалуй, одно. Надо применять графическое представление решения и показа результатов этого решения. В демонстрационном варианте ОГЭ предложена система двух линейных неравенств и графические представления вариантов ответов. Полезно понимать, что главным здесь является решение конкретных неравенств и понимание геометрического смысла полученного решения.
- Теория к заданию №13
- Задание 13 ОГЭ по математике — неравенства
- Задание №13 ОГЭ по математике
- Теория к заданию №13
- Разбор типовых вариантов задания №13 ОГЭ по математике
- Первый вариант задания
- Второй вариант задания
- Третий вариант задания
- Демонстрационный вариант ОГЭ 2019
- Четвертый вариант задания
- Пятый вариант задания
- 📹 Видео
Теория к заданию №13
Неравенством называется выражение вида: a b (a ≥ b)
Полезным для нас окажется метод интервалов:
Для решения линейного неравенства достаточно выполнить действия, аналогичные действию решений линейных уравнений. Однако, в отличие от линейных уравнений следует проявлять внимательность при выполнении операций деления или умножения на отрицательное число – в этих случаях знак неравенства будет меняться на противоположный!
Для решения этого примера вначале раскроем скобки, не забывая, что -3 умножается на -7 и дает + 21:
2 x – 3 x + 21 ≤ 3
Затем приводим подобные, перенося числа в правую сторону:
2 x – 3 x ≤ 3 – 21
Нам необходимо умножить неравенство на -1, чтобы получить диапазон x, не забывая, что при этом меняется знак неравенства:
Таким образом, мы получаем, что x должен быть больше либо равен 18.
pазбирался: Даниил Романович | обсудить разбор | оценить
Укажите множество решений неравенства: 7 x — x 2
Существуют несколько способов решения квадратных неравенств, но я приведу самый простой и надежный. В начале выносим x за скобку, так как это неполное квадратное неравенство:
pазбирался: Даниил Романович | обсудить разбор | оценить
Укажите множество системы неравенств:
Решение системы линейных неравенств сводится к решению линейного неравенства с дальнейшим анализом промежутков. В начале действуем аналогично первому случаю: переносим числа в правую часть, оставляя x слева:
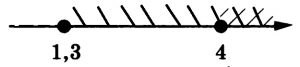
В отличие от первого примера, решение более простое, но в данном случае нужно сравнить промежутки и выбрать общий. Первое неравенство требует, чтобы x был больше 4, а второе – более 1,3, на координатной прямой это будет выглядеть следующим образом:
Промежутки перекрывают друг друга начина с 4, значит ответ выглядит следующим образом (не забываем, что неравенство нестрогое):
pазбирался: Даниил Романович | обсудить разбор | оценить
Итак, решим систему неравенств – оставим х в левой части, а остальное перенесём в правую, получим: х ≤ 0 -2,6 х ≥ 1 – 5 Вычислив, получаем ответ: х ≤ -2,6 х ≥ -4 Найдем его на координатной прямой – это №2.
pазбирался: Даниил Романович | обсудить разбор | оценить
Укажите решение неравенства:
Выполняем тождественные преобразования неравенства и приводим его к простейшему виду. Для этого сначала группируем слагаемые, перенося те, что с «х», в левую сторону, а свободные члены в правую:
Находим х. Знак неравенства при этом поменяется на противоположный, поскольку делить будем на –2, т.е. на отрицательное число:
Далее на коорд.прямой теперь нужно отложить точку со значением 3,5, причем точка будет закрашенная, т.к. знак неравенства нестрогий: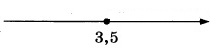 
Т.к. знак полученного неравенства «≤», то выделить следует часть прямой слева от точки 3,5: 
Это графическое решение соответствует ответу под №2.Ответ: 2
pазбирался: Даниил Романович | обсудить разбор | оценить
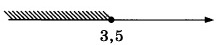
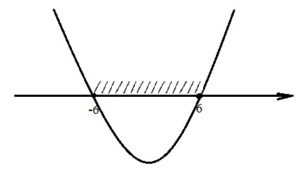
Укажите неравенство, решение которого изображено на рисунке.
Тут нужно сразу отметить два важных момента.
- Графическим решением неравенств из вариантов ответа является парабола, которая пересекает координатную ось в точках, соответствующих
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
1) х 2 –36≤0 х 2 ≤36
Корни этого неравенства равны ±6. Поскольку знак неравенства «меньше», то для ответа следует взять ту часть параболы, которая располагается ниже коорд.оси. Получаем:
Полученный промежуток-решение не соответствует заданному в качестве ответа в условии. 2) х 2 +36≥0 х 2 ≥–36 Это неравенство не имеет решений, поскольку для получения решения здесь требуется извлечь
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
pазбирался: Даниил Романович | обсудить разбор | оценить
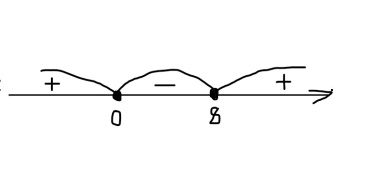
Вынесем -х за скобки: -х(-8 + х) ≥ 0
Теперь разделим на -1, не забывая изменить знак неравенства на противоположный: х(х – 8) ≤ 0
Найдем нули функции, приравняв каждый множитель к нулю: х=0 и х – 8=0, найдем х из второго уравнения: х=8.
Итак, имеем нули функции 0 и 8.
Теперь расставляем их на числовом луче и решаем неравенство методом интервалов.
Теперь находим промежуток чисел, соответствующий неравенству х(х – 8) ≤ 0, т.е. промежуток отрицательных или равных нулю чисел. Это будет промежуток [0; 8]
В соответствии с его номером, это будет ответ под №3.
pазбирался: Даниил Романович | обсудить разбор | оценить
Видео:Линейные неравенства и системы на ОГЭ ЗАДАНИЕ 13Скачать
Задание 13 ОГЭ по математике — неравенства
Как решать задание 13 ОГЭ по математике? Материал для подготовки к ОГЭ.
Для выполнения задания 13 необходимо уметь решать уравнения, неравенства и их системы.
С видами заданий на данной позиции в КИМах можно подробнее ознакомиться в кодификаторе.
Решение типовых задач № 13 на ОГЭ по математике
| Карточки для отработки задания 13 с ответами |
→ скачать (неравенства)
Автор: Е. А. Ширяева
Изменения в КИМ 2021 года по сравнению с 2020 годом коснулись задания №13.
В рамках усиления акцента на проверку применения математических знаний в различных ситуациях количество заданий уменьшилось на одно за счет объединения заданий на преобразование алгебраических (задание 13 в КИМ 2020 г.) и числовых выражений (задание 8 в КИМ 2020 г.) в одно задание на преобразование выражений на позиции 8 в КИМ 2021 г.
Видео:ОГЭ. ЗАДАНИЕ-13. НЕРАВЕНСТВА.Скачать
Задание №13 ОГЭ по математике
В тринадцатом задании ОГЭ по математике модуля Алгебра у нас проверяют знания преобразований — правила раскрытия скобок, выноса переменных за скобки, приведение дробей к общему знаменателю и знания формул сокращенного умножения.
Суть задания сводится к упрощению заданного в условии выражения: не стоит сразу подставлять значения в исходное выражение. Необходимо сначала упростить его, а затем подставить значение — все задания построены таким образом, что после упрощения требуется совершить всего одно или два простых действия.
Необходимо учитывать допустимые значения переменных, входящие в алгебраические выражения, использовать свойства степени с целым показателем, правила извлечения корней и формулы сокращенного умножения.
Ответом в задании является целое число или конечная десятичная дробь.
Теория к заданию №13
Прежде всего вспомним, что такое степень и правила обращения со степенями:
Кроме этого, нам понадобятся формулы сокращенного умножения:
(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 – b 2 = (a + b)(a – b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 = (a + b)( a 2 — ab + b 2 )
a 3 – b 3 = (a – b)( a 2 + ab + b 2 )
Правила операций с дробями:
Разбор типовых вариантов задания №13 ОГЭ по математике
Первый вариант задания
Найдите значение выражения: (x + 5) 2 — x (x- 10) при x = — 1/20
Решение:
В данном случае, как и почти во всех заданиях №7, необходимо сначала упростить выражение, для этого раскроем скобки:
(x + 5) 2 — x (x — 10) = x 2 + 2 • 5 • x + 25 — x 2 + 10x
Затем приведем подобные слагаемые:
x 2 + 2 • 5 • x + 25 — x 2 + 10x = 20 x + 25
Далее подставим x из условия:
20 x + 25 = 20 • (-1/20) + 25 = — 1 + 25 = 24
Второй вариант задания
Найдите значение выражения:
при a = 13, b = 6,8
Решение:
В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.
Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй — в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:
Далее выносим из числителя второй дроби a:
Подставляем значение a = 13:
Третий вариант задания
Найдите значение выражения:
при x = √45 , y = 0,5
Решение:
Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю.
Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно:
Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления.
5 y — (3 x + 5 y) = 5 y — 3 x — 5 y = — 3 x
Тогда дробь примет вид:
Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим:
Подставим значение y = 0,5:
— 1 / (5 • 0,5) = — 1 / 2,5 = — 0,4
Демонстрационный вариант ОГЭ 2019
Найдите значение выражения
Решение:
В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа.
Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе:
Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a.
Запишем конечную дробь:
Вычислим её значение, подставив числа из условия:
Четвертый вариант задания
Найдите значение выражения:
Решение:
Выполним тождественные преобразования выражения, чтобы упростить его.
1-й шаг – переход от деления дробей к их умножению:
далее в знаменателе второй дроби сворачиваем выражение по ф-ле сокращенного умножения (используем ф-лу для квадрата суммы):
теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:
Подставляем числовое значение для х в полученное выражение и находим результат:
Пятый вариант задания
Найдите значение выражения:
Решение:
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:
теперь переходим от деления дробей к их умножению:
затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя ф-лу сокращенного умножения для разности квадратов:
Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений):
Подставим полученные значения в выражение и найдем конечный результат:
📹 Видео
Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать
Неравенства. 2 правила для решения | Математика ОГЭ 2022 | УмскулСкачать
Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать
ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать
13 задание ОГЭ по математике. Квадратные неравенства | Математика ОГЭ | УмскулСкачать
Лайфхак для решения квадратных неравенств / Решаем 13 задание в ОГЭ по математикеСкачать
Неравенства №13 из ОГЭ. Линейные неравенства. Системы неравенств.Скачать
Решаем линейные уравнения на ОГЭ по математике 2022. Блок №1Скачать
ОГЭ за одну минуту, математика задание 13, неравенство.Скачать
ОГЭ Задание 13 НеравенстваСкачать
Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать
ОГЭ математика. Задание 13. Линейное неравенство.Скачать
Линейные уравнения в ОГЭ | Математика ОГЭ 2022 | УмскулСкачать
Рациональные уравнения. ОГЭ номер 21 | ЕГЭ номер 13 | Математика | TutorOnlineСкачать
ОГЭ. Задание 13. Линейные неравенстваСкачать
Линейные и квадратные уравнения №9 из ОГЭ.Скачать
ОГЭ математика задание 13 (бывшие 15) все неравенства. УРОК 1 Линейные неравенства Ященко решу ОГЭСкачать
13 задание ОГЭ по математикеСкачать
