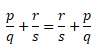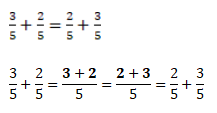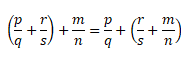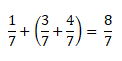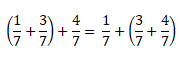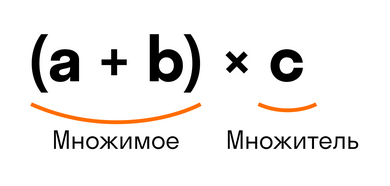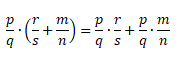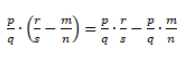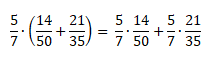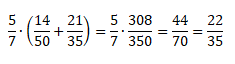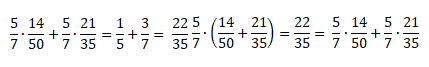О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Переместительный закон сложения
- Сочетательный закон сложения
- Переместительный закон умножения
- Сочетательный закон умножения
- Пример
- Распределительный закон умножения
- Пример 1
- Пример 2
- Пример 3
- Задания для самопроверки
- Математика. 5 класс
- Урок по теме «Распределительный закон умножения»
- Ход урока
- 1 этап. Организационный момент урока – 2 мин.
- 2 этап. Проверка домашнего задания – 5 мин.
- 📸 Видео
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Переместительный закон сложения
Начнем изучать основные законы математики со сложения натуральных чисел.
Переместительный закон сложения
От перестановки мест слагаемых сумма не меняется. С помощью переменных его можно записать так:
m + n = n + m
Переместительный закон сложения работает для любых чисел.
Если прибавить шестерку к двойке — получим восьмерку. И наоборот, прибавим двойку к шестерке — снова получим восьмерку. Это доказывает справедливость переместительного закона сложения.
Приведем пример с весами, которые используют продавцы в магазинах.
Если мы положим на одну чашу весов 3 килограмма конфет, а на другую — такие же 3 килограмма конфет, то стрелка весов будет на нейтральной позиции. Это говорит нам о том, что чаши действительно весят одинаково.
При этом неважно, как будут лежать конфеты, в каком порядке. Если перемешать конфеты в пакете, как шары в лотерейном мешке — их вес не изменится и будет по-прежнему 3 килограмма. От перестановки мест конфет их сумма, то есть вес, не меняется.
Поэтому, между выражениями 8 + 2 и 2 + 8 можно поставить знак равенства. Это значит, что их сумма равна:
Формула переместительного закона для обыкновенных дробей:
Чтобы сложить две дроби с одинаковым знаменателем, нужно сложить числители, а знаменатель оставить прежним. Вот так:
Видео:Распределительный закон умножения. Объяснение. МАТЕМАТИКА 6 класс. Много примеров.Скачать

Сочетательный закон сложения
Сочетательный закон сложения помогает группировать слагаемые для удобства их вычислений.
Сочетательный закон сложения: два способа
- Результат сложения нескольких слагаемых не зависит от порядка действий.
- Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.
Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.
Рассмотрим сумму из трех слагаемых:
Чтобы вычислить это выражение, можно сначала сложить числа 1 и 3 и к полученному результату прибавить 4. Чтобы было удобнее, можно сумму 1 и 3 взять в скобки — так мы поймем, что ими нужно заняться в первую очередь:
- 1 + 3 + 4 = (1 + 3) + 4 = 4 + 4 = 8
Или по-другому: сложим числа 3 и 4 и к результату прибавим 1:
- 1 + 3 + 4 = 1 + (3 + 4) = 1 + 7 = 8
В обоих случаях получается один и тот же результат — что и требовалось доказать.
Между выражениями (1 + 3) + 4 и 1 + (3 + 4) можно поставить знак равенства, так как они равны одному и тому же значению:
Отразим сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Формула сочетательного закона для обыкновенных дробей:
Например, если к сумме одной седьмой и трёх седьмых прибавить четыре седьмых, то в результате получим восемь седьмых.
Переставим скобки — к одной седьмой прибавим сумму трёх седьмых и четырех седьмых. И снова ответ будет восемь седьмых.
Значит, сочетательный закон справедлив и для обыкновенных дробей.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Видео:РАСПРЕДЕЛИТЕЛЬНОЕ СВОЙСТВО УМНОЖЕНИЯСкачать

Переместительный закон умножения
С каждым новым правилом решать задачки по математике все интереснее.
Переместительный закон умножения
От перемены мест множителей произведение не меняется. То есть, если множимое и множитель поменять местами — их произведение никак не изменится.
Проверим, действительно ли это так. Умножим пятерку на двойку, а потом наоборот:
В обоих случаях получили один ответ — значит между выражениями 5 * 2 и 2 * 5 можно поставить знак равенства.
Переместительный закон умножения с помощью переменных выглядит так:
a * b = b * a
Видео:Математика 5 класс (Урок№9 - Распределительный закон.)Скачать

Сочетательный закон умножения
Рассмотрим еще один полезный закон в математике.
Сочетательный закон умножения
Если выражение состоит из нескольких сомножителей, то их произведение не зависит от порядка действий.
Другими словами, умножайте числа в любом порядке — как вам больше нравится.
Это выражение можно вычислить в любом порядке. Давайте сначала перемножим числа 2 и 3, а полученный результат умножим на 4:
А теперь по-другому: перемножим числа 3 и 4, а результат умножим на 2:
- 3 * 4 = 12
- 2 * 12 = 24
- 2 * 3 * 4 = 24
Тот же ответ! Значит между выражениями (2 * 3) * 4 и 2 * (3 * 4) можно поставить знак равенства, так как они равны одному значению.
- (2 * 3) * 4 = 2 * (3 * 4)
- 6 * 4 = 2 * 12
- 24 = 24
Для любых натуральных чисел a, b и c верно равенство:
a * b * с = (a * b) * с = a * (b * с)
Пример
Вычислить: 5 * 6 * 7 * 8.
Это выражение можно вычислять в любом порядке. Вычислим слева направо:
5 * 6 * 7 * 8 = 1680
Видео:Раскрытие скобок. 6 класс.Скачать

Распределительный закон умножения
Для умножения есть еще один закон — распределительный. На математике в 6 классе он звучит так:
Распределительный закон умножения
- Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
- Чтобы сумму чисел умножить на число, нужно каждое слагаемое отдельно умножить на число и полученные произведения сложить.
То есть при помощи распределительного закона умножения можно умножить сумму на число и число на сумму. Проверим на примере:
Сначала выполним действие в скобках:
В главном выражении (3 + 5) * 2 заменим выражение в скобках на восьмерку:
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое в скобках, нужно умножить на 2, а потом сложить полученные результаты:
- (3 + 5) * 2 = 3 * 2 + 5 * 2
- 3 * 2 = 6
- 5 * 2 = 10
- 6 + 10 = 16
Отразим распределительный закон умножения с помощью переменных:
(a + b) * c = a * c + b * c
Выражение в скобках (a + b) — это множимое. Тогда переменная с — множитель, так как они соединены знаком умножения.
Из переместительного закона умножения мы знаем, что от перемены мест множимого и множителя произведение не изменится.
Если множимое (a + b) и множитель c поменять местами, то получим выражение c * (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для такого умножения можно применять распределительный закон умножения. Переменную c можно умножить на каждое слагаемое в скобках:
c * (a + b) = c * a + c * b
Пример 1
Умножим пятерку на каждое слагаемое в скобках и сложим полученные результаты:
5 * (3 + 2) = 5 * 3 + 5 * 2 = 15 + 10 = 25
Пример 2
Найти значение выражения 2 * (5 + 2).
Умножим двойку на каждое слагаемое в скобках и сложим полученные результаты:
2 * (5 + 2) = 2 * 5 + 2 * 2 = 10 + 4 = 14
Если в скобках не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. А после из полученного первого числа вычесть второе число.
Пример 3
Умножим четверку на каждое число в скобках. Из полученного первого числа вычтем второе число:
4 * (6 − 2) = 4 * 6 − 4 * 2 = 24 − 8 = 16
Распределительный закон умножения для суммы обыкновенных дробей:
Распределительный закон умножения для разности обыкновенных дробей:
Проверим справедливость этого закона:
Посчитаем, чему равна левая часть равенства.
Теперь посчитаем, чему равна правая часть равенства.
Так мы доказали справедливость распределительного закона.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Задания для самопроверки
Давайте потренируемся! Решите примеры и сравните с ответами — только чур, не подглядывать 🙂
Задание 1. Найти значение выражения: 8 * (1 + 6).
Задание 2. Применить распределительный закон умножения: 2 * (9 + 5).
Задание 3. Решить в порядке выполнения действий: 3 * (6 + 4) + 7 * (8 + 2).
Задание 4. Решить выражение: 4 * (5 + 4) + 9 * (3 + 2).
Задание 5. Применить распределительный закон умножения: 13 * (3 + 8) + 5 * (4 + 2)
Видео:Решаем линейные уравнения на ОГЭ по математике 2022. Блок №1Скачать

Математика. 5 класс
Конспект урока
Перечень вопросов, рассматриваемых в теме:
— распределительный закон умножения;
Раскрытие скобок – это замена выражения со скобками на равное ему выражение без скобок, а также от произведений числа и разности – к разности произведений.
Вынесение общего множителя за скобки – это замена суммы произведений к произведению числа и суммы, а также от разности произведений к произведению числа и разности.
Распределительный закон умножения: чтобы число умножить на сумму двух чисел, надо это число умножить на каждое слагаемое и полученные произведения сложить.
- Никольский С. М. Математика: 5 класс. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2017. – 272 с.
- Потапов М. К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.
- Бурмистрова Т. А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
- Потапов М. К. Математика: дидактические материалы. 6 класс. // М. К. Потапов, А. В. Шевкин – М.: Просвещение, 2010.- 118 с.
- Чесноков А. С. Дидактические материалы по математике 5 класс. // А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с.
Теоретический материал для самостоятельного изучения
Для любых чисел а, b и с верно равенство:
а ∙ (b + c) = a ∙ b + a ∙ с
Оно выражает распределительный закон умножения: чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.
Посмотрим, как можно применить этот закон на практике.
Вычислим и сравним значения выражений 4 ∙ (3 + 5) и 4 ∙ 3 + 4 ∙ 5.
4 ∙ (3 + 5) = 4 ∙ 8 = 32
4 ∙ 3 + 4 ∙ 5 = 12 + 20 = 32
Оба выражения имеют одинаковое значение, поэтому можно сделать вывод, что распределительный закон справедлив.
4 ∙ (3 + 5) = 4 ∙ 3 + 4 ∙ 5 = 32
Отметим, что распределительный закон верен не только для двух, но и для любого числа слагаемых. Например, верно следующее равенство:
4 ∙ (5 + 6 + 7 + 8) = 4 ∙ 5 + 4 ∙ 6 + 4 ∙ 7 + 4 ∙ 8
Кроме того, если b больше или равно с (b ≥ c), то верно равенство:
а ∙ (b – c) = a ∙ b – a ∙ с
Например: 7 ∙ (9 – 5) = 7 ∙ 9 – 7 ∙ 5.
Говорят, что в произведениях 4 ∙ (3 + 5) и 7 ∙ (9 – 5) раскрыли скобки и получили соответствующую сумму 4 ∙ 3 + 4 ∙ 5 и разность 7 ∙ 9 – 7 ∙ 5.
Переход от произведений числа и суммы и числа, и разности соответственно к сумме произведений и разности произведений называют раскрытием скобок.
а ∙ (b + c) = a ∙ b + a ∙ с
а ∙ (b – c) = a ∙ b – a ∙ с
Переход от суммы произведений к произведению числа и суммы и от разности произведений к произведению числа и разности соответственно называют вынесением общего множителя за скобки.
a ∙ b + a ∙ с = а ∙ (b + c)
a ∙ b – a ∙ с = а ∙ (b – c)
Вынесение общего множителя за скобки позволяет упрощать вычисления.
- 27 ∙ 41 + 27 ∙ 59 = 27 ∙ (41 + 59) = 27 ∙ 100 = 2700
- 55 ∙ 67 – 55 ∙ 66 = 55 ∙ (67 – 66) = 55 ∙ 1 = 55
- 356 ∙ 73 + 644 ∙ 27 + 73 ∙ 644 + 27 ∙ 356 = 73 ∙ (356 + 644) + 27 ∙ (644 + 356) = 73 ∙ 1000 + 27 ∙ 1000 = 1000 ∙ (73 + 27) = 1000 ∙ 100 = 100000
Любое из чисел a, b и с в равенствах а ∙ (b + c) = a ∙ b + a ∙ с и а ∙ (b – c) = a ∙ b – a ∙ с (если b ≥ c) может быть нулём, поэтому распределительный закон верен и для целых неотрицательных чисел.
Разбор решения заданий тренировочного модуля
№ 1. Вычислите, используя распределительный закон 125∙(8+ 10).
Решение: для вычисления значения данного выражения раскроем скобки 125∙(8+ 10)=125∙8+ 125∙10= 1000+ 1250= 2250.
№ 2. Найдите значение выражения 5 ∙ 38 – 30 ∙ 5. Выберите правильный ответ.
Варианты ответа: 40; 45; 42; 35.
Решение: для вычисления значения данного выражения, применим распределительный закон умножения. Вынесем общий множитель 5 за скобки:
5 ∙ 38 – 30 ∙ 5 = 5 ∙ (38 – 30) = 5 ∙ 8 = 40
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Урок по теме «Распределительный закон умножения»
Разделы: Математика
1. Тип урока по основной дидактической цели — урок закрепления и систематизации знаний; выработки умений по применению распределительного закона умножения.
1) образовательные: систематизировать, расширить и углубить знания, формировать умение применять распределительный закон умножения при решении задач, продолжить выявление пробелов в знаниях и ликвидировать их.
2) развивающие: способствовать развитию наблюдательности, умения находить наиболее рациональные пути решения задач, развивать вычислительные навыки, продолжить формирование у учащихся умения самостоятельно работать.
3) воспитательные: воспитание чувства ответственности за результат, воспитывать культуру умственного труда, развивать коммуникативные качества личности, развивать способность самооценки.
Активизировать знания учащихся о распределительном законе, расширить и углубить знания по теме. Создать условия для того, чтобы учащиеся могли применять их на практике при решении примеров, уравнений и текстовых задач. Развивать устойчивый познавательный интерес к изучению математики. Вырабатывать умение самокритично оценивать свои знания и выбирать задания соответственно своему уровню знаний.
4. Знании, умения, навыки и качества, которые закрепят ученики в ходе урока:
продолжить выработку умений применять распределительный закон умножения при упрощении выражений, путем вынесения общего множителя за скобки, для более рационального счета, решать уравнения и составлять их при решении текстовых задач.
Слайдовая презентация урока “Распределительный закон умножения”, классная доска, ноутбук, экран, медиа-проектор, учебник “Математика, 5” автор Н.Я. Виленкин, В.И. Жохов, индивидуальные оценочны листы, карточки с заданиями к “Математической эстафете”, карточки с задачами, карточки с тестами, листы с заданиями для самостоятельной работы трех уровней.
Ход урока
1 этап. Организационный момент урока – 2 мин.
Учитель приветствует учащихся, сообщает тему урока (Приложение 1. Слайд №1), эпиграф (Приложение 1. Слайд №2), ставит перед классом цели урока (Приложение 1. Слайд №3), план урока (Приложение 1.Слайд №4), правила заполнения индивидуальных оценочных листов.
Здравствуйте, ребята! Сегодня на уроке нам предстоит повторить распределительный закон умножения и подготовиться к контрольной работе. Будьте внимательны! Наш урок
будет состоять из нескольких этапов, вы их видите на слайде (Приложение 1. Слайд №3), оценку за урок мы будем накапливать (Приложение 1. Слайд №5) и в конце урока подведем итоги. Ваша работа будет считаться успешной и получаете оценку “5”, если вы наберете от 37 до 41 баллов, если вы набираете от 29 до 36 баллов, то вы получаете оценку “4”, если от 20 до 28 – оценку “3”, менее 20 баллов — оценку “2”.
2 этап. Проверка домашнего задания – 5 мин.
Цель этапа: подчеркнуть важность выполнения домашнего задания, искать рациональные пути решения для упрощения вычислительной работы, выявление пробелов в знаниях.
Знания: вынесение за скобки общего множителя числового или буквенного.
Умения: составление уравнений и их решение, нахождение неизвестной компоненты.
Форма работы: фронтальная, самопроверка.
Используемые цифровые ресурсы или их компоненты – (Приложение 1. Слайд №6).
1. Упростите выражение.
2. Вычислите наиболее простым способом.
3. Решите уравнение.
4. Решите задачу.
В семье 4 человека: мама, папа, сын и дочь. Вместе им 110 лет. Мама старше дочери в 5 раз, и младше отца на 6 лет, а дочь младше сына в 2 раза. Сколько лет каждому из членов семьи?
| № задания | Ответ: |
| №1. а) | 97а |
| б) | 9m+48 |
| в) | 0 |
| г) | 100 |
| №2. а) | 246900 |
| б) | 25(26-24)+23(24-22)+21(22-20)+19(20-18)+17(18-16)+15(16-14)= = 2(25+15+23+17+21+19) = 2(40+40+40) = 240 |
| №3. а) | x = 2 |
| б) | x = 5 |
| в) | x = 3 |
| №4. | Уравнение: x+2x+5x+5x+6=110; х = 8; 8 лет, 16 лет, 40 лет, 46 лет |
Деятельность учителя – учитель зачитывает верные ответы к заданиям домашней работы.
Деятельность ученика – сверяет свои ответы с готовыми на экране.
Задания домашней работы проецируются на экран с готовыми ответами. Учащимся предлагается сравнить их со своими ответами и оценить каждое верно выполненное задание 1 баллом. Максимальное число баллов на данном этапе – 10. Полученные баллы учащиеся заносят в индивидуальный оценочный лист.
— Ребята, а каким способом вы решали задание №2?
Часть учащихся решали по действиям, другие с помощью распределительного закона. Сравниваем и делаем вывод, что второй способ не требует больших вычислений и он более рациональный. При разборе задачи №4 выясняем, что учащиеся принимали за х, какое уравнение составили и какой ответ получили.
3 этап. “Разминка” — тест с взаимопроверкой (в парах) – 7мин.
Цель этапа: актуализировать знания по теме, осуществлять самостоятельную деятельность на уроке, развивать коммуникативные качества.
Умения: применять распределительный закон умножения, находить ошибки в решении товарища, составить уравнение по тексту задачи и решить его.
Форма работы: индивидуальная, а во время проверки — в парах.
Используемые цифровые ресурсы — (Приложение 1. Слайды №7, №8, №9).
Деятельность учителя – консультирует детей, дает рекомендации по выполнению заданий теста, контролирует самостоятельность решения.
Деятельность ученика: самостоятельно выполняет задания, затем после обмена работами осуществляет проверку работы товарища, сравнивая с готовыми ответами на экране, оценивает баллами его работу. Заносит баллы в индивидуальный оценочный лист. Готовые ответы проецируются на экран. Задания №1 и №2 оцениваются в 1 балл,
№3 – 2 балла. Максимальное число баллов – 9.
Во время проверки теста учитель предлагает учащимся прочитать законы умножения.
Спрашивает ребят: “Кто не ошибся и набрал максимальное количество баллов?”
Большинство ребят сделали верно, настроение улучшается, повышается мотивация, ребята стремятся к дальнейшим победам.
1. Соедините линиями соответствующие законы умножения:
Оценка: 3 балла ( по баллу за каждое верное соединение).
1. Отметить знаком “+” верно выполненные выражения.
Оценка – 4 балла за каждое верно выбранное или верно не выбранное выражение.
2. Составьте уравнение к задаче:
Ученик задумал число, умножил его на 8, затем это же число отдельно умножил на 15 и результаты сложил. В сумме получилось 276. Какое число задумал ученик?
Оценка – 2 балла.
4 этап. “Математическая эстафета” — 8 мин.
Цель этапа: выявление пробелов в знаниях, развитие коммуникативных качеств учащихся.
Умения: вынесение общего множителя за скобки, находить неизвестную компоненту в уравнениях.
Форма работы: групповая — в парах и группа 8-9 человек.
Используемые цифровые ресурсы — (Приложение 1. Слайд №10, №11).
Деятельность учителя – консультирует по правилам игры. Организует проверку результатов.
На последней парте каждого ряда находятся по листу с 9 заданиями (по два задания каждой парте). Эти же задания высвечены на экране (Приложение 1. Слайд №10).
Задания 1), 3), 5), 7), 9) — Решить уравнение;
Задания 2), 4), 6), 8) — Упростить выражение.
| 1 ряд | 2 ряд | 3 ряд | |||
| 1 | 25x + 87x = 336 | 1 | 66y – 29y = 74 | 1 | 54x + 41x = 190 |
| 2 | 41y — 21y + y | 2 | 92x + x – 33x | 2 | 63a + a – 51a |
| 3 | 16a – 9a + 5 = 75 | 3 | 25k – 16k + 5 = 86 | 3 | 39x – 27x + 15 = 63 |
| 4 | 45b + 24b – 69b | 4 | 74c + 47c – 121c | 4 | 45y + 31y – 76y |
| 5 | 18x + 62x — 15 = 145 | 5 | 16a + 73a – 26 = 152 | 5 | 58x + 96x – 54 = 100 |
| 6 | 99k – 19k + k — 81 | 6 | 46d – 24d + d — 23 | 6 | 61k – 57k + k — 5 |
| 7 | 44x — 22x = 880 | 7 | 77y – 55y = 660 | 7 | 99d — 11d = 176 |
| 8 | n + 2n – 3n + 2008 | 8 | 9t – 5t – 4t + 2009 | 8 | x + 5x – 6x + 2010 |
| 9 | 55x – 13x – 17x = 625 | 9 | 47y + 53y – 80y = 180 | 9 | 42 y + 98y – 40y = 600 |
Ответы к “Математической эстафете”:
| 1 ряд | 2 ряд | 3 ряд | |||
| 1 | x = 3 | 1 | y = 2 | 1 | x = 2 |
| 2 | 21y | 2 | 60x | 2 | 13a |
| 3 | a = 10 | 3 | k = 9 | 3 | x = 4 |
| 4 | 0 | 4 | 0 | 4 | 0 |
| 5 | x = 2 | 5 | a = 2 | 5 | x = 1 |
| 6 | 81k — 81 | 6 | 23d — 23 | 6 | 5k — 5 |
| 7 | x = 40 | 7 | y = 30 | 7 | d = 2 |
| 8 | 2008 | 8 | 2009 | 8 | 2010 |
| 9 | x = 25 | 9 | y = 9 | 9 | y = 6 |
Деятельность ученика – решают задания, записывают решение в общий лист, который передают вперед, следующей паре учащихся. Затем команды обмениваются листами с решениями и осуществляют проверку, соотнося с готовыми ответами на экране (Приложение 1. Слайд №11), выставляют баллы — по 1 за каждое верно решенное задание. Максимум — 9 баллов. Первой, сдавшей решение команде, добавляется 2 балла, второй – 1 балл. Учащиеся заносят командные баллы в оценочный лист.
5. “Решение задач с помощью уравнений”. – 7 мин.
Цель этапа: развитие логико – смыслового мышления.
Умения: введя переменную х и переведя текст задачи на математический язык, составить математическую модель — в виде уравнения, решить его, ответить на вопрос задачи.
Форма работы: групповая — 3 ряда — 3 команды.
Используемые цифровые ресурсы — (Приложение 1. Слайд №12, №13)
Деятельность учителя – выбирает любого из учеников для решения у доски, контролирует правильность решения, оценивает объяснение решения у доски, грамотно заданные вопросы с места. Уравнения и ответы высвечиваются на экране.
Деятельность ученика – решают задачу своей команды на местах, поправляют ответ участников своей команды, решающих у доски ( в случае ошибок отвечающего), задают вопросы соперникам, изображая непонимание. Рефлексия: осознание учеником деятельности: того как, каким способом получен результат, какие при этом встречались затруднения, как они были устранены, и что чувствовал ученик при этом.
Верно решившие задачу, заносят в оценочный лист — 3 балла.
Маша, Оля и Таня пошли в лес за грибами. Маша собрала в 3 раза больше грибов, чем Таня, а Оля в 2 раза больше, чем Таня. Сколько грибов собрала каждая девочка, если всего они собрали 84 гриба?
В лесу жили хамелеоны. Синих хамелеонов было в 7 раз больше, чем красных, а красных в 5 раз больше, чем зеленых. Сколько хамелеонов каждого цвета жило в лесу, если всего их было насчитано 123 хамелеона?
В зоопарке жили хищные животные. Тигров было в 2 раза больше, чем ягуаров и в 4 раза меньше, чем пантер. Сколько хищников каждого вида жило в зоопарке, если всего насчитывалось 55 животных?
6 этап. Самостоятельная разно — уровневая работа с самопроверкой — 10 мин.
Вначале этапа учащимся демонстрируются 3 уровня работы и предлагается выбрать самим, оценив реально свои возможности, для получения наибольшего балла
(Приложение 1. Слайды №14, №15, №16).
Цель этапа: проверка знаний по теме, с учетом уровня приобретённых знаний.
Умения: применять распределительный закон умножения для рационального счета, при решении уравнений, составлять математическую модель к текстовой задаче.
Форма работы: индивидуальная работа.
Используемые цифровые ресурсы или их компоненты — (Приложение 1. Слайды №14 – 19)
Деятельность учителя – организация контроля за самостоятельностью решения и процедуры проверки, сбор карточек с решениями.
Деятельность ученика – учащиеся, которые выбрали задание 1 уровня – заполняют пропуски в решении заданий, 2 уровня – решают типичные задания, 3 уровня – олимпиадные задания. Проводят проверку, сверяя с готовыми ответами на экране, выставляют баллы в индивидуальные оценочные листы. Задания 1 и 2 уровня сложности оцениваются — 1 баллом, их всего шесть, итого максимум – 6 баллов, задания 3 уровня сложности, требующие больше времени на их выполнение – 2 баллами, их четыре, итого – 8 баллов. Рефлексия: осознание учеником деятельности: того как, каким способом получен результат, какие при этом встречались затруднения , как они были устранены, и что чувствовал ученик при этом.
Методы: самоконтроль полученных знаний.
Если позволит время, то можно разобрать на доске задания третьего уровня : №1(б), №2, составить уравнение к заданию №3.
Задания к самостоятельной работе:
№1. Упростите выражение. Заполните пропуски.
а) 15x + 20x + x = (_ + _ + _)• x = ?•x,
б) 24a – 12a – 78 = (_ — _) • а — 78 = _•а — _,
в) y + 55y – 56y + 45 = (_ + _ — _) • y + _ = _y + _ = _,
№2. Решите уравнение.
| а) 78x + 92x = 340 | б) 49y – 27y + 34 = 100 |
| (_ + _) • x = 340 | (_ — _)•y + 34 = 100 |
| _ • x = 340 | _ y = 100 _ 34 |
| x = 340: _ | _ y = _ |
| x = _ | y = _:_ |
| Ответ: | y = _. Ответ: |
№3. По данной к задаче таблице составь уравнение:
| Собрали яблок | |
| Петя | 4х яблок |
| Галя | х яблок |
| Коля | 7х яблок |
Вместе дети собрали — 72 яблока.
Задания к самостоятельной работе. Оценка – максимум 6 баллов.
№1. Упростите выражение.
а) 46х + 87х – 38х;
б) 84y — 37y + 41y – 124;
в) 65а + 36а – а – 100;
№2. Решите уравнение:
а) 43х + 2• 3х = 98; б) 59а – 38а – 95 = 10.
№3. Решите задачу.
| Выразить через “х” сколько животных | |
| кенгуру | В 5 раз больше, чем пони |
| пони | В 2 раза больше, чем бегемотов |
| бегемоты |
Всего в зоопарке было 26 животных.
Уровень 3. Задания к высокому уровню.
Оценка — по 2 балла за каждое верно решенное задание.
№1. Вычислить как можно более простым способом:
а) 5•2 + 5•22 + 5• 222 + 5 •2222;
б) 33•25 — 25•23 + 10•15 — 40•5.
№2. Решите уравнение.
(((7х – 2•2х)+6х) – 7х) + 2•4х = 1000.
№3. Решите задачу.
| Выразить через “х” | |
| сорок | в 2 раза больше, чем синиц и в 3 раза меньше, чем снегирей |
| синиц | |
| снегирей |
Всего на дереве сидело — 18 птиц.
7 этап. Подведение итогов урока — 5 мин.
Цель этапа: подведение итогов урока, достижения целей урока.
Используемые цифровые ресурсы или их компоненты — (Приложение 1. Слайд №20)
Деятельность учителя- отмечает в какой мере достигнуты цели урока, на что требуется обратить внимание. Комментирует результаты работы учащихся. Выставляет оценки, созданная во время урока “ситуация успеха” принесла удовлетворенность результатами, радость преодоленной трудности.
Деятельность ученика- подсчитывают баллы в индивидуальных оценочных листах, выставляют оценки, в соответствии с заданными критериями.
8. Дифференцированное творческое домашнее задание — 1 мин.
Цель этапа: развитие творческого мышления учащихся
Деятельность учителя- ориентирует на домашнее задание, которое предусматривает уровневую дифференциацию, ориентировано на достигнутый уровень знаний.
Деятельность ученика — записывает домашнее задание.
Спасибо за урок, дети! (Приложение 1. Слайд №21).
📸 Видео
Сочетательное и распределительное свойство умножения. 5 классСкачать

Задание №1 "Как решать уравнения через распределительный закон". Математика 5-6, Алгебра 7-8 классСкачать

Математика 6 класс (Урок№29 - Распределительный закон.)Скачать

Линейное уравнение с двумя переменными. 7 класс.Скачать

Математика 5 класс (Урок№64 - Законы умножения. Распределительный закон.)Скачать

Как решать линейные уравнения Решите уравнение 5 класс 6 класс 7 класс Как решать простое уравнениеСкачать

Алгебра 7 Линейное уравнение с одной переменнойСкачать

Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Линейные и квадратные уравнения №9 из ОГЭ.Скачать

Как решать линейные уравнения #математика #математика7классСкачать

Линейное уравнение с одной переменнойСкачать

ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать