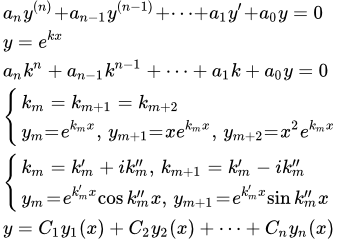Линейные однородные дифференциальные уравнения первого порядка с постоянным коэффициентом

Видео:15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Вид общего решения

Рассмотрим линейное однородное дифференциальное уравнение с постоянными коэффициентами:
(1) .
Его решение можно получить следуя общему методу понижения порядка.

Однако проще сразу получить фундаментальную систему n линейно независимых решений и на ее основе составить общее решение. При этом вся процедура решения сводится к следующим шагам.

Ищем решение уравнения (1) в виде . Получаем характеристическое уравнение:
(2) .
Оно имеет n корней. Решаем уравнение (2) и находим его корни . Тогда характеристическое уравнение (2) можно представить в следующем виде:
(3) .
Каждому корню соответствует одно из линейно независимых решений фундаментальной системы решений уравнения (1). Тогда общее решение исходного уравнения (1) имеет вид:
(4) .

Действительные корни

Рассмотрим действительные корни. Пусть корень однократный. То есть множитель входит в характеристическое уравнение (3) только один раз. Тогда этому корню соответствует решение
.

Пусть – кратный корень кратности p . То есть
. В этом случае множитель входит в характеристическое уравнение (3) p раз:
.
Этим кратным (равным) корням соответствуют p линейно независимых решений исходного уравнения (1):
; ; ; . ; .

Комплексные корни

Рассмотрим комплексные корни характеристического уравнения (3). Выразим комплексный корень через действительную и мнимую части:
.
Поскольку коэффициенты исходного уравнения (1) действительные, то кроме корня имеется комплексно сопряженный корень
.

Пусть комплексный корень однократный. Тогда паре корней соответствуют два линейно-независимых решения уравнения (1):
; .

Пусть – кратный комплексный корень кратности p . Тогда комплексно сопряженное значение также является корнем характеристического уравнения кратности p и множитель входит в разложение на множители (3) p раз:
.
Этим 2 p корням соответствуют 2 p линейно независимых решений:
; ; ; . ;
; ; ; . .

После того как фундаментальная система линейно независимых решений найдена, по формуле (4) получаем общее решение уравнения (1).

Видео:Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Примеры решений задач

Пример 1

Найти общее решение однородного дифференциального уравнения седьмого порядка с постоянными коэффициентами:
.

Ищем решение в виде . Составляем характеристическое уравнение:
.
Преобразуем его:
;
;
.

Рассмотрим корни этого уравнения. Мы получили четыре комплексных корня кратности 2:
; .
Им соответствуют четыре линейно-независимых решения исходного уравнения:
; ; ; .

Также мы имеем три действительных корня кратности 3:
.
Им соответствуют три линейно-независимых решения:
; ; .

Общее решение исходного уравнения имеет вид:
.

Пример 2

Это однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Ищем решение в виде . Составляем характеристическое уравнение:
.
Решаем квадратное уравнение.
.

Мы получили два комплексных корня:
.
Им соответствуют два линейно-независимых решения:
.
Общее решение уравнения:
.

Пример 3

Найти общее решение однородного дифференциального уравнения четвертого порядка с постоянными коэффициентами:
.

Ищем решение в виде . Составляем характеристическое уравнение:
.
Выносим за скобки:
(П3.1) .
Решаем квадратное уравнение :
.
Получили два комплексных корня, которые обозначим как . Тогда . Перепишем характеристическое уравнение (П3.1) в эквивалентном виде:
.
Отсюда видно, что оно имеет два кратных корня кратности 2, и два комплексно сопряженных корня . Кратным корням соответствуют два линейно независимых решения:
;
.
Комплексно сопряженным корням , соответствуют решения
.
Общее решение:
.

Автор: Олег Одинцов . Опубликовано: 29-07-2013 Изменено: 27-10-2020

Видео:Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Линейные дифференциальные уравнения с постоянными коэффициентами. Специальная часть Ax + B

Решение было получено и оформлено с помощью сервиса:
Дифференциальные уравнения

Пример 2. y’’ -2y’ + y = x-1
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -2 r + 1 = 0
D = (-2) 2 — 4 • 1 • 1 = 0


Корни характеристического уравнения:
Корень характеристического уравнения r₁ = 1 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e x
y₂ = xe x
Общее решение однородного уравнения имеет вид:

Рассмотрим правую часть:
f(x) = x-1
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = x-1, Q(x) = 0, α = 0, β = 0.
Следовательно, число α + βi = 0 + 0i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида:
y * = Ax + B
Вычисляем производные:
y’ = A
y» = 0
которые подставляем в исходное дифференциальное уравнение:
y» -2y’ + y = -2A + (Ax + B) = x-1
или
A•x-2A+B = x-1
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
A = 1
-2A + B = -1
Откуда: A = 1;B = 1;
Частное решение имеет вид:
y * = x + 1
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример 3. y’’ +6y’ + 9y = 9x 2 +12x-43

Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 +6 r + 9 = 0
D = 6 2 — 4 • 1 • 9 = 0


Корни характеристического уравнения:
Корень характеристического уравнения r₁ = -3 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e -3x
y₂ = xe -3x
Общее решение однородного уравнения имеет вид:

Рассмотрим правую часть:
f(x) = 9•x 2 +12•x-43
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 9•x 2 +12•x-43, Q(x) = 0, α = 0, β = 0.
Следовательно, число α + βi = 0 + 0i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида:
y * = Ax 2 + Bx + C
Вычисляем производные:
y’ = 2•A•x+B
y» = 2•A
которые подставляем в исходное дифференциальное уравнение:
y» + 6y’ + 9y = 2•A + 6(2•A•x+B) + 9(Ax 2 + Bx + C) = 9•x 2 +12•x-43
или
9•A•x 2 +12•A•x+2•A+9•B•x+6•B+9•C = 9•x 2 +12•x-43
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
9A = 9
12A + 9B = 12
2A + 6B + 9C = -43
Решая ее методом Гаусса, находим:
A = 1;B = 0;C = -5;
Частное решение имеет вид:
y * = x 2 -5
Таким образом, общее решение дифференциального уравнения имеет вид:
y = C₁ e -3 x + C₂ xe -3 x + x 2 -5

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

📸 Видео

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

4. Однородные дифференциальные уравнения (часть 1)Скачать

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Дифференциальные уравнения, 4 урок, Линейные дифференциальные уравнения первого порядкаСкачать

Однородное дифференциальное уравнениеСкачать

Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать

Линейные однородные дифференциальные уравнения 1-го порядка. Высшая математика.Скачать

Однородные дифференциальные уравнения первого порядка #calculus #differentialequation #maths #Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать