Ортогональным дополнением непустого подмножества [math]M[/math] евклидова пространства [math]mathbb[/math] называется множество векторов, ортогональных каждому вектору из [math]M[/math] . Ортогональное дополнение обозначается
forall mathbfin M Bigr>.[/math]
Рассмотрим примеры ортогональных дополнений евклидова пространства.
1. Ортогональным дополнением нулевого подпространства [math] <mathbf> triangleleft mathbb[/math] служит все пространство [math]mathbb colon, <mathbf>^= mathbb[/math] . Ортогональным дополнением всего пространства является его нулевое подпространство [math]mathbb^= <mathbf>[/math] .
2. Пусть в пространстве [math][/math] радиус-векторов (с началом в точке [math]O[/math] ) за даны три взаимно перпендикулярных радиус-вектора [math]overrightarrow[/math] , [math]overrightarrow[/math] и [math]overrightarrow[/math] . Тогда ортогональным дополнением вектора [math]overrightarrow[/math] является множество радиус- векторов на плоскости, содержащей векторы [math]overrightarrow[/math] и [math]overrightarrow[/math] , точнее, [math]<overrightarrow>^= operatorname(overrightarrow,overrightarrow)[/math] . Ортогональным дополнением векторов [math]overrightarrow[/math] и [math]overrightarrow[/math] служит множество радиус-векторов на прямой, содержащей вектор [math]overrightarrowcolon <overrightarrow,overrightarrow>^= operatorname (overrightarrow)[/math] . Ортогональным дополнение трех заданных векторов служит нулевой радиус-вектор: [math]<overrightarrow, overrightarrow, overrightarrow>^= <overrightarrow>[/math] .
3. В пространстве [math]P_2(mathbb)[/math] многочленов степени не выше второй со скалярным произведением (8.29) задано подмножество [math]P_0(mathbb)[/math] — многочленов нулевой степени. Найдем ортогональное дополнение этого подмножества. Для этого приравняем нулю скалярное произведение многочлена [math]p_2(x)=ax^2+bx+c[/math] на постоянный многочлен [math]p_0(x)=dcolon[/math] [math]langle p_2(x),p_0(x)rangle= acdot0+bcdot0+ccdot d=0[/math] . Поскольку величина [math]d[/math] произвольная, то [math]c=0[/math] . Следовательно, ортогональным дополнением подмножества [math]P_0(mathbb)[/math] является множество многочленов из [math]P_0(mathbb)[/math] с нулевым свободным членом.
Видео:ОртогональностьСкачать
Свойства ортогонального дополнения
Рассмотрим свойства ортогональных дополнений подмножеств n-мерного евклидова пространства [math]mathbb[/math] .
1. Ортогональное дополнение [math]M^[/math] непустого подмножества [math]Msubset mathbb[/math] является линейным подпространством, т.е. [math]M^ triangleleft mathbb[/math] , и справедливо включение [math]Msubset (M^)^[/math] .
В самом деле, множество [math]M^[/math] замкнуто по отношению к операциям сложения векторов и умножения вектора на число, так как сумма двух век торов, ортогональных [math]M[/math] , ортогональна [math]M[/math] , и произведение вектора, ортогонального [math]M[/math] , на любое число является вектором, ортогональным [math]M[/math] . До кажем включение [math]Msubset (M^)^[/math] . Пусть [math]mathbfin M[/math] , тогда [math]langle mathbf,mathbfrangle=0[/math] для любого вектора [math]mathbfin M^[/math] . Но это означает, что [math]mathbfsubset (M^)^[/math] .
2. Пересечение любого непустого подмножества [math]Msubset mathbb[/math] со своим ортогональным дополнением есть нулевой вектор: [math]Mcap M^= <mathbf>[/math] .
Действительно, только нулевой вектор ортогонален самому себе.
3. Если [math]L[/math] — подпространство [math]mathbb
(Ltriangleleft mathbb)[/math] , то [math]mathbb=Loplus L^[/math] .
Действительно, возьмем в [math]L[/math] ортогональный базис [math](mathbf)= (mathbf_1, ldots,mathbf_k)[/math] . До полним его векторами [math](mathbf)= (mathbf_,ldots, mathbf_n)[/math] до ортогонального базиса [math](mathbf),,(mathbf)[/math] всего пространства [math]mathbb[/math] . Тогда произвольный вектор [math]mathbfin mathbb[/math] можно представить в виде суммы
где [math]mathbfin L[/math] , а [math]mathbfin L^[/math] , так как [math]langle mathbf,mathbf_irangle= sum_^mathbflangle mathbf_j, mathbf_i rangle_<_>=0[/math] для [math]i=1,ldots,k[/math] . Следовательно, любой вектор пространства [math]mathbb[/math] раскладывается по подпространствам [math]L[/math] и [math]L^[/math] , т.е. [math]mathbb= L+L^[/math] . Эта алгебраическая сумма является прямой суммой по свойству 2, поскольку [math]Lcap L^=<mathbf>[/math] . Следовательно, [math]mathbb=Loplus L^[/math] .
4. Если [math]Ltriangleleft mathbb[/math] , то [math]dim<L^>= dimmathbb-dim[/math] .
5. Если [math]L[/math] — подпространство [math]mathbb[/math] , то [math]L=(L^)^[/math] .
Из первого свойства следует включение [math]Lsubset(L^)^[/math] . Докажем, что [math](L^)^subset L[/math] . Действительно, пусть [math]mathbfin (L^)^[/math] . По свойству 3: [math]mathbf=mathbf+mathbf[/math] , где [math]mathbfin L,
mathbfin L^[/math] . Найдем скалярное произведение
Следовательно, [math]langle mathbf,mathbfrangle=0[/math] , и согласно аксиоме 4 скалярного произведения [math]mathbf=mathbf[/math] , поэтому [math]mathbf=mathbf+ mathbf= mathbf+mathbf=mathbfin L[/math] . Значит, [math](L^)^subset L[/math] . Из двух включений [math]Lsubset (L^)^[/math] и [math](L^)^ subset L[/math] следует равенство [math]L=(L^)^[/math] .
6. Если [math]L_1triangleleft mathbb[/math] и [math]L_2triangleleft mathbb[/math] , то [math](L_1+L_2)^=L_1^cap L_2^[/math] и [math](L_1cap L_2)^= L_1^+ L_2^[/math] .
Последние свойства аналогичны свойствам алгебраических дополнений.
Видео:Ортогональное дополнение (задача 1366)Скачать
Нахождение ортогонального дополнения подпространства
Ранее для описания подпространств линейных пространств использовались два способа описания (внешний и внутренний). Рассмотрим применение этих способов описания для нахождения ортогональных дополнений подпространств. Учитывая изоморфизм евклидовых пространств, будем рассматривать арифметическое пространство [math]mathbb^n[/math] со скалярным произведением (8.27).
Для заданного подпространства [math]Ltriangleleft mathbb^n[/math] требуется найти его ортогональное дополнение [math]L^[/math] . В зависимости от способа описания подпространства [math]L[/math] используем одно из следующих двух утверждений.
1. Если подпространство [math]Ltriangleleft mathbb^n[/math] задано как линейная оболочка [math]L=operatorname(a_1,ldots,a_k)[/math] столбцов матрицы [math]A= begina_1&cdots&a_kend[/math] , то множество решений однородной системы [math]Ax=o[/math] является его ортогональным дополнением [math]L^triangleleft mathbb^n[/math] , т.е.
2. Если подпространство [math]Ltriangleleft mathbb^n[/math] задано как множество решений однородной системы [math]Ax=o[/math] [math]m[/math] уравнений с [math]n[/math] неизвестными, то линейная оболочка столбцов [math]a_1^T,ldots,a_m^T[/math] транспонированной матрицы [math]A^T=begina_1^T&cdots&a_m^Tend[/math] является его ортогональным дополнением [math]L^triangleleft mathbb^n[/math] , т.е.
где [math]a_i^T[/math] — i-й столбец матрицы [math]A^T[/math] .
Докажем, например, первое утверждение. Линейное однородное уравнение
1. В отличие от алгебраического дополнения [math]L^[/math] подпространстве [math]Ltriangleleft mathbb[/math] ортогональное дополнение [math]L^[/math] находится однозначно.
2. Ортогональное дополнение [math]L^[/math] подпространства [math]Ltriangleleft mathbb[/math] в силу свойства 3 является также и алгебраическим дополнением. Это обстоятельстве учитывалось при нахождении алгебраических дополнений при помощи утверждений (8.16) и (8.17), которые по существу совпадают с утверждениями (8.34) и (8.35).
Пример 8.19. В примере 8.10 для линейного подпространства [math]L= operatorname[(t-1)^2,(t+1)^3][/math] пространства [math]P_3(mathbb)[/math] многочленов не более, чем 3-й степени, было найдено алгебраическое дополнение
Доказать, что это алгебраическое дополнение является ортогональным дополнением подпространства [math]L[/math] евклидова пространства [math]P_3(mathbb)[/math] со скалярным произведением (8.29).
Решение. Для решения задачи достаточно показать, что образующие подпространства [math]L:[/math]
ортогональны образующим алгебраического дополнения [math]L^:[/math]
Видео:Ортогональное дополнение. ПримерСкачать
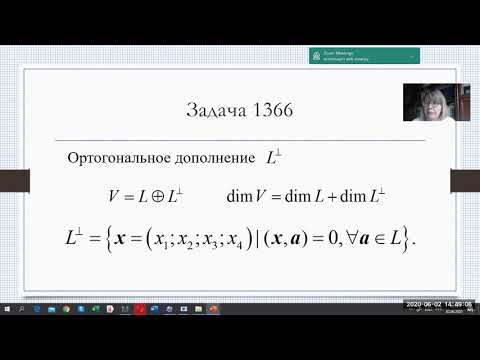
Ортогональное дополнение. Ортогональная проекция вектора на подпространство
Пусть Е — евклидово пространство, а L — его подпространство. Множество L 1 — векторов в Е, ортогональных к каждому вектору подпространства L, называют ортогональным дополнением к подпространству L.
Теорема 8.6. Ортогональное дополнение IA к подпространству L евклидова пространства Е является подпространством в Е.
> Пусть уi,y2 € ZA. Тогда для любого вектора х ? L имеем: (ж, г/1) = 0 и (х,у2) = 0. Следовательно,
т.е. вектор у + у2 ортогонален любому вектору х € L. Это означает, что У1+У2 € ZA. Мы доказали, что сумма любых двух векторов множества ZA принадлежит ZA. Аналогично для любого действительного числа Л и любого х € L имеем:
т.е. вектор Л у ортогонален любому вектору х е L, а значит, принадлежит ZA. Таким образом, множество ZA замкнуто относительно сложения векторов и умножения векторов на числа и, следовательно, является подпространством. ?
Теорема 8.7. Конечномерное евклидово пространство Е является прямой суммой любого своего подпространства L и его ортогонального дополнения ZA, т.е. ортогональное дополнение к подпространству является его прямым дополнением.
> Пусть в пространстве L выбран ортогональный базис, состоящий из векторов ai, 02, . а&. Дополним его до ортогонального базиса пространства Е векторами fk+i, fk+2, •••, fn и по построенному базису
разложим произвольный вектор х из Е. Тогда получим 
где положено
Вектор у принадлежит подпространству Z, поскольку он является линейной комбинацией векторов базиса в L. Покажем, что вектор z принадлежит ортогональному дополнению LА Для этого замечаем, что по построению векторы fk+i, fk+2, fn ортогональны базисным
векторам ai, Это очевидное следствие теоремы о размерности суммы подпространств (см. теорему 4.23). ?
Следствие 8.3. Ортогональным дополнением к подпространству ZA является подпространство L.
> Так как каждый вектор из L ортогонален каждому вектору из ZA, то подпространство L содержится в (ZA)A Кроме того, выполняются соотношения Е = L 0 ZA, Е = (L— L )- L ф ZA, и по предыдущему следствию подпространства L и (ZA) 1 — имеют одинаковую размерность. Поэтому эти подпространства совпадают. ?
Следствие 8.4. Если L — подпространство в евклидовом пространстве Е, то любой вектор х € Е имеет разложение
где хо G L, х 1 — G /А. Такое разложение единственно.
> Это утверждение — фактически расшифровка утверждения, что Е = L Ф ZA. ?
Пример 8.9. В четырехмерном пространстве Е± скалярное произведение в заданном базисе определено формулой (8.5). Построить ортогональное дополнение ZA для подпространства L = (а^аг), где a, = (1,1,1, l) r , а2 = (1, -1,1,1) т .
Решение. Векторы а и а2 составляют базис в L. Дополним эту систему до базиса в Е± векторами Ъ и 62, удовлетворяющими условиям 
и положим L = (61,62)- Векторы 61, 62 являются решениями системы из двух уравнений (ai,x) = 0, (а,2,х) = 0, и в качестве их можно взять любую фундаментальную систему решений, например, 61 = (—1,0,1,0) т , 62 = (—1,0,0,1) т . Из выбора векторов 61 и 62 следует, что они составляют базис в L L , т.е. L = L L . ?
Пусть L — подпространство евклидова пространства Е. Каждый вектор у ? Е может быть единственным способом представлен в виде
где уо ? L, а вектор у 1 — ортогонален к каждому вектору из L, т.е. у 1 — ? L х . Вектор уо называют ортогональной проекцией вектора у на пространство L и обозначают прьУ, а вектор y L называют ортогональной составляющей вектора у. Очевидно, что если у ? L, то прьу = у, и, наоборот, если прьу = : Действительно, пусть у — произвольный вектор, опущенный из конца вектора х на подпространство L и х 1 — — ортогональная составляющая вектора х, т.е. перпендикуляр, опущенный из конца вектора х на подпространство L. Тогда
поскольку концы векторов у их 1 лежат в L. Поэтому
так как векторы у — х 1 — их 1 ортогональны. ?
Доказанные утверждения является естественным обобщением известного из элементарной геометрии утверждения о том, что перпендикуляр короче любой наклонной, опущенной из той же точки на плоскость.
Длину ортогональной составляющей х 1 — вектора х принимают за кратчайшее расстояние от вектора х до подпространства L.
Ортогональная проекция вектора у на подпространство L является частным случаем проекции вектора на подпространство параллельно подпространству L2, являющемуся прямым дополнением к L (см. разд. 4.11). В случае ортогональной проекции Ь2 = Ь 1 .
На практике при отыскании ортогональной проекции вектора х на подпространство L = (ai, а2, •••?> &fc) поступают следующим образом. В разложении
вектора х на ортогональную проекцию жо = npLT и ортогональную составляющую х 1 — вектор Xq можно представить в виде линейной комбинации 
Тогда равенство х = Хо + х 1 принимает вид:
Для отыскания коэффициентов oi, 02, . о& умножим равенство (8.16) скалярно на векторы а, а2, . ак- Учитывая, что (а^аг 1- ) = = (а2,х ± ) = . = (ак,х?*?) = 0, получаем систему линейных уравнений
относительно неизвестных оц, а2, . а к. Из этой системы находят коэффициенты oi, а2, . о^. В матричной форме равенство (8.15) и система (8.17) записываются в виде
где А = (oi, а2. а*,) — матрица, для которой столбцами являются столбцы координат векторов а, а2, . а&; о — (01,02, . о*;) т — столбец высоты к. Использование системы (8.17), или, что тоже самое системы (8.19), указывает на то (см. п.8.21), что отыскание коэффициентов ai, а2, . ак для равенства (8.15) равносильно решению методом наименьших квадратов системы А о = х с неизвестным столбцом
Если система векторов oi, 2, • ••, ftfc линейно независимая, то в равенстве (8.19) матрица А т А невырожденная, так как она представляет собой матрицу Грама этой системы векторов (см. теорему 8.1). В этом случае из уравнения (8.19) однозначно определяется столбец а: 
Учитывая равенство (8.18), заключаем, что 
Пример 8.10. Для вектора х = (3,6,0) т найти ортогональную проекцию Xq на подпространство L = (а^аг) и ортогональную составляющую т х , если ay = (1, —1,0) т , т .
Решение. Запишем xq = npL.x в виде хд = ау ау + Коэффициенты ау и «2 можно найти, решив систему (8.17), которая в данном случае имеет вид:
Вычислим все скалярные произведения. В результате получим
Решая систему относительно неизвестных од иаг, находим, что од = = су2 = 3. Таким образом, пр/,т = Зау + Заг = (0,3,3) т и х^ = = х — npLT = (3,3, —3) т .
Поскольку векторы а у, а2 линейно независимые, то можно также воспользоваться формулой (8.20). Вычислив
Заметим, что если е = (ei, е2,еп) — ортоиормированный базис в евклидовом пространстве Е, а подпространство L является линейной оболочкой части базисных векторов, например, L = (ei, е2. е*,), то для любого вектора
ортогональная проекция прь-т совпадает с суммой слагаемых в разложении х по базису, соответствующих векторам, порождающим L. а ортогональная проекция — с суммой всех остальных слагаемых, т.е.
Например, для вектора х = (1,2, 3,4,5) т проекция на подпространство L = (б1,е2,ез) равна Xq = (1,2,3,0,0) т , и его ортогональная составляющая х 1 — = (0,0,0,4, 5) т . ?
📹 Видео
7. Линейные подпространства. Формула Грассмана. Многообразия.Скачать
Линейная оболочка. Базис и размерностьСкачать
4.1 Сумма и пересечение подпространств.Скачать
15. Однородная система линейных уравнений / фундаментальная система решенийСкачать
Как разложить вектор по базису - bezbotvyСкачать
Линейные уравнения с одной переменной, содержащие переменную под знаком модуля. 6 класс.Скачать
1 5 Подпространство линейного пространстваСкачать
Матричный метод решения систем уравненийСкачать
§43 Линейные пространстваСкачать
Тимашев Д.А. - Линейная алгебра и геометрия.Лекции-13.Симметрические билинейные и квадратичные ф-цииСкачать
Лекция №1. Системы линейных уравненийСкачать
Смирнов С. В. - Линейная алгебра. Семинары - Линейные подпространства и операции над нимиСкачать
Связь линейных систем и линейных оболочек. ТемаСкачать
Типовые задачи линейной алгебры. Консультация для студентов 1 курса. Лунина М.А.Скачать
Линал I Л8. Линейное пространство. Наборы векторов (ЛЗ, ЛНЗ, полные). БазисСкачать
01.02.2022 Подпространства и системы линейных уравнений, Сумма подпространств.Скачать
