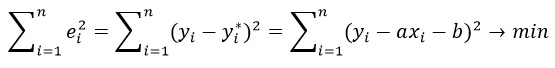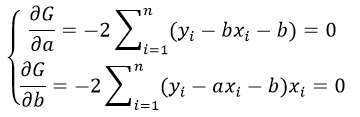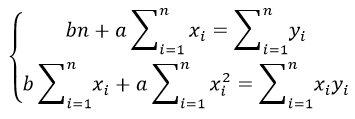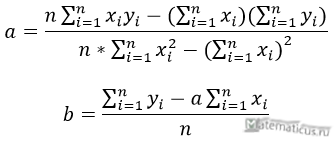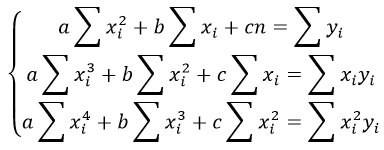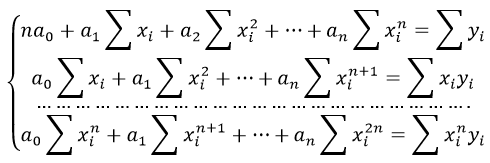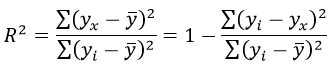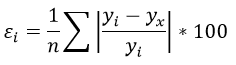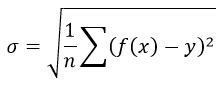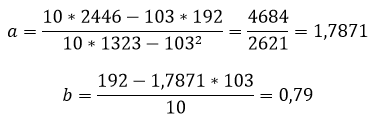Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид
y=ax+b
a, b – коэффициенты линейного уравнения регрессии;
x – независимая переменная;
y – зависимая переменная.
Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов:
частные производные функции приравниваем к нулю
отсюда получаем систему линейных уравнений
Формулы определения коэффициентов уравнения линейной регрессии:
Также запишем уравнение регрессии для квадратной нелинейной функции:
Система линейных уравнений регрессии полинома n-ого порядка:
Формула коэффициента детерминации R 2 :
Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):
Чем меньше ε, тем лучше. Рекомендованный показатель ε
Формула среднеквадратической погрешности: 
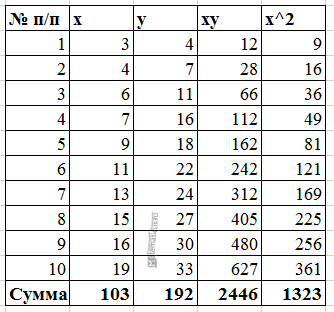
Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:
| x | y |
| 3 | 4 |
| 4 | 7 |
| 6 | 11 |
| 7 | 16 |
| 9 | 18 |
| 11 | 22 |
| 13 | 24 |
| 15 | 27 |
| 16 | 30 |
| 19 | 33 |
Решение
Расчеты значений суммы, произведения x и у приведены в таблицы.
Расчет коэффициентов линейной регрессии:
при этом средняя ошибка аппроксимации равна:
ε=11,168%
Получаем уравнение линейной регрессии с помощью метода наименьших квадратов:
y=1,7871x+0,79
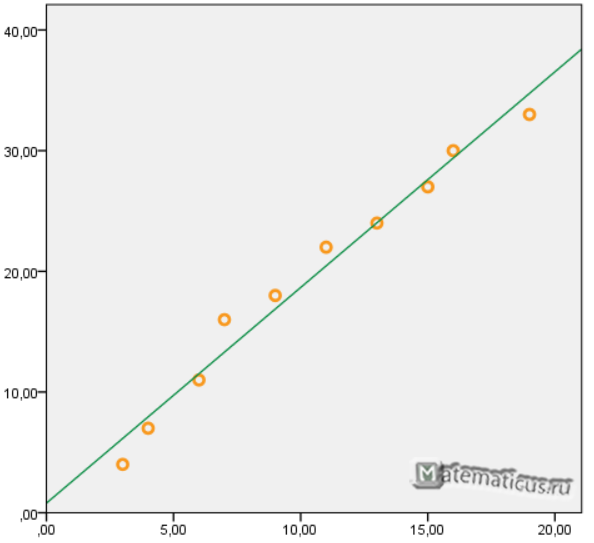
График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек
Коэффициент корреляции равен 0,988
Коэффициента детерминации равен 0,976
Видео:Построение уравнения линейной регрессии методом наименьших квадратов.Скачать
Решения задач: метод наименьших квадратов
Метод наименьших квадратов применяется для решения различных математических задач и основан на минимизации суммы квадратов отклонений функций от исходных переменных. Мы рассмотриваем его приложение к математической статистике в простейшем случае, когда нужно найти зависимость (парную линейную регрессию) между двумя переменными, заданными выборочными данным. В этом случае речь идет об отклонениях теоретических значений от экспериментальных.
Краткая инструкция по методу наименьших квадратов для чайников: определяем вид предполагаемой зависимости (чаще всего берется линейная регрессия вида $y(x)=ax+b$), выписываем систему уравнений для нахождения параметров $a, b$. По экспериментальным данным проводим вычисления и подставляем значения в систему, решаем систему любым удобным методом (для размерности 2-3 можно и вручную). Получается искомое уравнение.
Иногда дополнительно к нахождению уравнения регрессии требуется: найти остаточную дисперсию, сделать прогноз значений, найти значение коэффициента корреляции, проверить качество аппроксимации и значимость модели. Примеры решений вы найдете ниже. Удачи в изучении!
Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать
Примеры решений МНК
Пример 1. Методом наименьших квадратов для данных, представленных в таблице, найти линейную зависимость
Пример 2. Прибыль фирмы за некоторый период деятельности по годам приведена ниже:
Год 1 2 3 4 5
Прибыль 3,9 4,9 3,4 1,4 1,9
1) Составьте линейную зависимость прибыли по годам деятельности фирмы.
2) Определите ожидаемую прибыль для 6-го года деятельности. Сделайте чертеж.
Пример 3. Экспериментальные данные о значениях переменных х и y приведены в таблице:
1 2 4 6 8
3 2 1 0,5 0
В результате их выравнивания получена функция Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
Пример 4. Данные наблюдений над случайной двумерной величиной (Х, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X.
Пример 5. Считая, что зависимость между переменными x и y имеет вид $y=ax^2+bx+c$, найти оценки параметров a, b и c методом наименьших квадратов по выборке:
x 7 31 61 99 129 178 209
y 13 10 9 10 12 20 26
Пример 6. Проводится анализ взаимосвязи количества населения (X) и количества практикующих врачей (Y) в регионе.
Годы 81 82 83 84 85 86 87 88 89 90
X, млн. чел. 10 10,3 10,4 10,55 10,6 10,7 10,75 10,9 10,9 11
Y, тыс. чел. 12,1 12,6 13 13,8 14,9 16 18 20 21 22
Оцените по МНК коэффициенты линейного уравнения регрессии $y=b_0+b_1x$.
Существенно ли отличаются от нуля найденные коэффициенты?
Проверьте значимость полученного уравнения при $alpha = 0,01$.
Если количество населения в 1995 году составит 11,5 млн. чел., каково ожидаемое количество врачей? Рассчитайте 99%-й доверительный интервал для данного прогноза.
Рассчитайте коэффициент детерминации
Видео:Метод наименьших квадратов, урок 1/2. Линейная функцияСкачать
МНК и регрессионный анализ Онлайн + графики
Данный онлайн-сервис позволяет найти с помощью метода наименьших квадратов уравнения линейной, квадратичной, гиперболической, степенной, логарифмической, показательной, экспоненциальной регрессии и др., коэффициенты и индексы корреляции и детерминации. Показываются диаграмма рассеяние и график уравнения регрессии. Также калькулятор делает оценку значимости параметров уравнения регрессии с помощью F-критерия Фишера, t-критерия Стьюдента и критерия Дарбина-Уотсона.
Можно задать уровень значимости и указать, до какого знака после запятой округлять расчётные величины.
Примечание: дробные числа записывайте через точку, а не запятую.
Степенная регрессия
Квадратичная регрессия
Кубическая регрессия
Показательная регрессия
Логарифмическая регрессия
Экспоненциальная регрессия
Округлять до
-го
знака после запятой.
💥 Видео
Как работает метод наименьших квадратов? Душкин объяснитСкачать
Метод наименьших квадратов. Случай линейной регрессииСкачать
Метод наименьших квадратов. Квадратичная аппроксимацияСкачать
Метод наименьших квадратовСкачать
Парная регрессия: линейная зависимостьСкачать
Метод наименьших квадратов. Регрессионный анализ.Скачать
Суть метода наименьших квадратов с примерами. Основы эконометрики в RСкачать
Метод наименьших квадратов. Парная регрессия расчет без Excel @economc #МНК #регрессия #корреляцияСкачать
11 1 Метод наименьших квадратов ВведениеСкачать
Метод наименьших квадратов (МНК)Скачать
Линейная регрессияСкачать
Метод наименьших квадратовСкачать
Алгоритмы. Аппроксимация линейной функцией по методу наименьших квадратовСкачать
ЦОС Python #1: Метод наименьших квадратовСкачать
Метод Наименьших Квадратов (МНК)Скачать
Метод наименьших квадратов. ТемаСкачать
Численные методы: Метод наименьших квадратовСкачать
