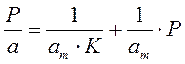Линейная форма уравнения адсорбции ленгмюра (6 видео)

Уравнение изотермы адсорбции Ленгмюра

Конечно, предположение, что молекулы адсорбируются с одинаковой вероятностью на любых участках поверхности, в том числе и уже занятых ранее — слишком грубое допущение, пригодное лишь для очень малых степеней покрытия.

Теория Ленгмюра позволяет учесть наиболее сильные отклонения от закона Генри, что связано с ограничением адсорбционного объема или поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества. Это положение уточняется следующими утверждениями.

1) Адсорбция локализована на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбента — образуется мономолекулярный слой.

2) Адсорбционные центры энергетически эквивалентны — поверхность адсорбента эквипотенциальна.

3) Адсорбированные молекулы не взаимодействуют друг с другом.

Простейший вывод уравнения Ленгмюра, данный Кисилевым, основан на рассмотрении химического (в случае хемосорбции) или квазихимического (в случае физической адсорбиии) равновесия молекула газа + свободное место↔адсорбированная молекула.

Для обычного выражения константы равновесия через концентрации участников рассматриваемого процесса необходимо условиться о способах их выражения. Концентрация адсорбированных молекул может быть выражена не только числом адсорбированных молекул на 1 м 2 поверхности, но и в относительных единицах через долю занятой поверхности (степень заполнения поверхности) θ. Тогда, в тех же единицах, концентрация свободных мест 1-θ. Концентрация молекул газа (а молях на миллилитр) может быть заменена пропорциональной ей величиной давления Р (равновесное давление адсорбата в объеме фазы, граничащей с адсорбентом). Такая свобода в выборе единиц рассматриваемых концентраций обусловлена тем, что соответствующие константы пропорциональности могут быть объединены с константой равновесия. Итак, константа равновесия

. (2.6)

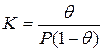
Решение этого уравнения относительно θ приводит к выражению

. (2.7)

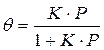
Если а, как и раньше, есть величина адсорбции (моль/см 2 или см 3 /г), а a_m — величина адсорбции, соответствующая полному заполнению поверхности (емкость монослоя, моль/см 2 ), то степень заполнения θ=a/a_m, (2.8)

т.е. 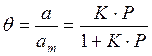, (2.9)

отсюда 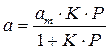(2.10)

В такой форме уравнение Ленгмюра широко известно. Оно содержит две константы: a_m, кратко называемая емкостью монослоя, и K — константа, зависящая от энергии адсорбции и температуры.

Итак, уравнение Ленгмюра – это уравнение монослойной адсорбции на однородной поверхности в отсутствие сил притяжения между молекулами адсорбата.

Посмотрим, какую форму примет уравнение при крайних значениях поверхностной концентрации адсорбированного вещества.

В области малых концентраций, т.е. при малых давлениях, КР >1, и единицей в знаменателе можно пренебречь:

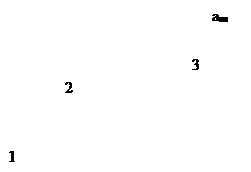
т.е. величина адсорбции стремится к пределу, при котором она уже практически не зависит от давления (участок 3 изотермы адсорбции). В промежуточной области (участок 2) зависимость адсорбции от давления описывается самим уравнением (2.10).

Рис. 2.5. Три участка изотермы адсорбции Ленгмюра

Таким образом, по модели Ленгмюра, вначале адсорбция растет пропорционально давлению газа, затем, по мере заполнения мест на поверхности, этот рост замедляется и, наконец, при достаточно высоких давлениях рост адсорбции практически прекращается, так как покрытие поверхности становится весьма близким к монослойному. Необходимо подчеркнуть, однако, что по этой модели завершение образования монослоя происходит лишь при бесконечно высоком давлении. Форма изотермы адсорбции, предсказываемая уравнением Ленгмюра, экспериментально наблюдается в случае химической адсорбции на однородных поверхностях. Для физической адсорбции такое соответствие наблюдается только в начальной области изотермы. При больших заполнениях не получается предсказываемого теорией приближения к насыщению и изотерма продолжает подъем с ростом давления, причем она становится даже более крутой.

Для удобной проверки приложимости уравнения Ленгмюра к экспериментальным данным преобразуем его в линейную форму. Разделим обе части уравнения (2.10) на Р:

. (2.13)

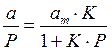
Перевернем дроби по обе части равенства:

. (2.14)

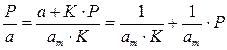
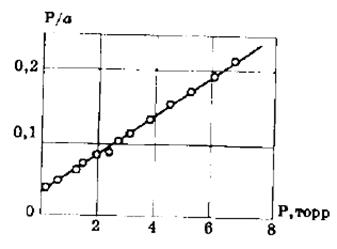
Если по оси абсцисс откладывать Р, а на оси ординат Р/а, то в случае выполнимости уравнения Ленгмюра экспериментальные точки должны укладываться на прямую. Начальной ординатой будет 1/(а_m∙К), тангенсом угла наклона прямой 1/а_m. Из того и другого выражения легко вычислить обе константы a_m и К. Пример такого построения показан на рис. 2.6, где экспериментальные точки для адсорбции бензола на графитированной саже, в соответствии с указанными ранее, легли па прямую только в области малых давлений (до Р/Р₀ =0.1).

Рис. 2.6. Изотерма адсорбции бензола при 20 о С на графитированной саже в координатах линейной формы уравнения Ленгмюра

Имеется немало примеров, когда уравнение Ленгмюра не выполняется. Объясняется это тем, что не оправдываются оба допущения теории об однородности поверхности и отсутствии взаимодействия молекул, особенно первое из них. Тот факт, что имеются случаи адсорбции на реальных неоднородных поверхностях, когда уравнение Ленгмюра все же удовлетворительно описывает экспериментальные данные, Брунауер объясняет тем, что в некотором интервале адсорбция происходит не на всей поверхности адсорбента, а только на части ее, именно на местах с примерно одинаковой теплотой адсорбции. Тогда в этом интервале уравнение Ленгмюра будет справедливо. После того, как эти места заполнены, начинает заполняться следующая серия мест с меньшей теплотой адсорбции. Поэтому для совокупности всех мест поверхности уравнение Ленгмюра может быть непригодно, а для части этих мест — справедливо. Отсюда, выполнимость его для разных адсорбентов зависит от соотношения участков с разной теплотой адсорбции.

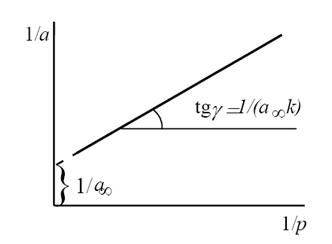
Константы уравнения (2.10) K и a_m могут быть определены графическим способом (рис. 2.7). Для этого уравнение Ленгмюра приводят к следующему линейному виду, разделив единицу на уравнение (2.10):

(2.15)

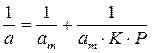
Рис. 2.7. Линейная форма уравнения изотермы Ленгмюра (a_∞=a_m)

Зная емкость монослоя, можно определить удельную поверхность адсорбента S_уд (м 2 /г или см 2 /г) если известна площадь ω, занимаемая частицей в плотном адсорбционном слое (площадь, занимаемая одной молекулой азота в адсорбционном слое ω = 0.162 нм 2 ):

, (16)

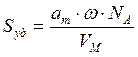
где а_m — емкость монослоя — это количество адсорбата, которое может разместиться в полностью заполненном адсорбционном слое толщиной в 1 молекулу — монослое – на поверхности единицы массы (1г) твердого тела; ω — средняя площадь, занимаемая молекулой адсорбата в заполненном монослое, N_A — число Авогадро (6,022·10 23 молекул/моль); V_M — молярный объем адсорбата (газа) (V_M = 22,41 л/моль=22,41∙10 -3 м 3 /моль).

Уравнение Ленгмюра можно использовать только при адсорбции в мономолекулярном слое. Это условие выполняется при хемосорбции, физической адсорбции газов при меньшем давлении и температуре выше критической.

Однако в большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поэтому остается возможность влияния поверхностных сил на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и пары адсорбируются при температуре ниже критической, т.е. образуются полимолекулярные слои на поверхности адсорбента, что можно представить как вынужденную конденсацию В этом случае используют уравнение БЭТ (Брунауер –Эммет — Теллер).

Пример 2.1. При адсорбции азота на активированном угле при 220К получены следующие данные:

Р, Па 5310 9800 18000 33000 70000

a, cм 3 /г 7 14 23 32 51

Плотность газообразного азота ρ=1,2506 кг/м 3 . Площадь, занимаемая одной молекулой азота в насыщенном монослое, составляет ω = 0.162 нм 2 . V_M — молярный объем адсорбата (газа) (V_M = 22,41 л/моль=22,41∙10 -3 м 3 /моль).

Постройте изотерму адсорбции в линейных координатах. Графически определите константы а_m и К уравнения Ленгмюра, пользуясь которыми, постройте изотерму Ленгмюра. Определите удельную поверхность активированного угля S_уд.

Решение. Линейная форма уравнения Ленгмюра выражается (2.15):

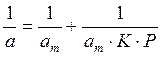
Определим 1/а_m и 1/ р:

(1/р)·10 -3 , Па 0,1883 0,1020 0,0556 0,0303 0,0143

1/а·, см 3 /г 0,143 0,071 0,043 0,031 0,020

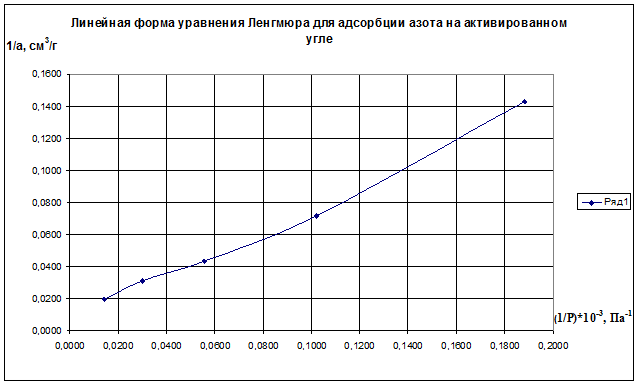
Строим график зависимости 1/а=f(1/р)∙10 -3 (рис.2.8). По графику находим 1/а_m как отрезок, отсекаемый прямой на оси ординат, для чего необходимо продлить полученную прямую до пересечения с осью ординат.

Рис.2.8. Линейная форма уравнения Ленгмюра для адсорбции азота на активированном угле

Уравнение прямой y=a+bx, имеет следующее формульное выражение:

Это выражение может быть определено с помощью регрессионного анализа в Microsoft Excel (встроенного пакета Анализ данных — Регрессия по значениям 1/а_m и 1/ р).

Из уравнения получим 1/a_m=0,00698 г/см 3 .

Откуда получим: a_m=143,35 см 3 /г.

Далее находят тангенс угла наклона прямой к оси абсцисс tgα=1/(a_m∙K) по графику (или по уравнению регрессии). tgα=0,70099. Тогда, зная значения a_m и tgα, можно определить K=9,95 кг/м 3 .

Теперь, зная константы а_m и К уравнения Ленгмюра, построим изотерму Ленгмюра, для чего рассчитаем по формуле (2.10) значения а для различных значений Р и получим:

Р, Па 5310 9800 18000 33000 70000

a, cм 3 /г 140,69 141,90 142,56 142,92 143,15

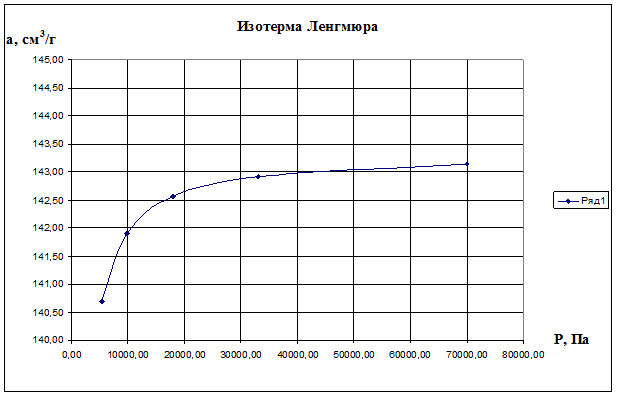
По данным значениям построим изотерму Ленгмюра а=f(P), представлена на рис.2.9.

Рис. 2.9. Изотерма Ленгмюра а=f(P)

По формуле (2.16) рассчитаем удельную поверхность активированного угля: 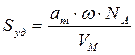и получим S_уд=624,05 м 2 /г.

В случае, когда известна плотность вещества (адсорбента) ρ и молярная масса M, а не известен V_M — молярный объем адсорбата удельную поверхность вещества (активированного угля) находят по формуле:

где a_m выражают в моль/кг.

Для азота М= 0,0280 кг/моль, ρ=1,2506 кг/м 3 .

Из расчетов видно, что два способа расчета S_уд дают почти одинаковые результаты.

Пример 2.2. Удельная поверхность непористой сажи равна 73,7м 2 /кг. Рассчитайте площадь, занимаемую молекулой бензола в плотном монослое, исходя из данных об адсорбции бензола на этом адсорбенте при 293 К.

Р, Па 1,03 1,29 1,74 2,50 6,67

а∙10 2 , моль/кг 1,57 1,94 2,55 3,51 7,58

Предполагается, что изотерма адсорбции описывается уравнением Ленгмюра.

Решение. Используем линейную форму записи уравнения Ленгмюра, заданную формулой (2.14):

Рассчитываем значения Р/а:

(Р/а)∙10 -2 , Па∙кг/моль 0,656 0,668 0,68 0,712 0,879

Р, Па 1,03 1,29 1,74 2,50 6,67

По этим данным строим график в координатах уравнения Ленгмюра в линейной форме P/a=f(P).

Из графика находим а_m= Р/(Р/а) = 25,2∙10 -2 моль/кг.

Удельная поверхность адсорбента связана с емкостью слоя а_m, выраженного в моль/кг, соотношением: S_уд=a_m∙ω∙N_A (2.18)

Площадь, занимаемая молекулой бензола в плотном монослое, равна

ω = S_уд/(a_m N_A) ==73,7 10 3 /(6,02 10 23 ∙25,210 -2 )=0,49∙10 -18 м 2 =0,49 нм 2 .

Содержание

Линейная форма уравнения адсорбции ленгмюра
Физическая химия
Главная > Документ
§4. Мономолекулярная адсорбция. Изотерма адсорбции Ленгмюра
§5 . Теория полимолекулярной адсорбции БЭТ
§6. Изотермы адсорбции и поверхностного натяжения растворов ПАВ Уравнение Шишковского
§7. Классификация и общая характеристика поверхностно-активных веществ. Правило Дюкло – Траубе
🎥 Видео

Видео:Практическое занятие 4. Адсорбция на границе твердое тело – газСкачать

Линейная форма уравнения адсорбции ленгмюра

Небольшая предыстория . В ходе изучения ПАВ американский химик и физик Ирвинг Ленгмюр выдвинул и математически обосновал идею об особом строении адсорбционных слоев. Он рассматривал ненасыщенный слой как двухмерный газ. По мере того как концентрация ПАВ увеличивается, происходит процесс, аналогичный конденсации двухмерного газа – молекулы образуют двухмерную пленку, которую Ленгмюр рассматривал как двухмерную жидкость. Если концентрация ПАВ в растворе неограниченно возрастает, то наступает момент предельного насыщения адсорбционного слоя, который приобретает вид частокола, так как предполагается, что слой имеет толщину, соответствующую длине адсорбированной молекулы. При этом адсорбция достигает предела. Эта теория была названа теорией мономолекулярного слоя, или монослоя.

Теория Ирвинга Ленгмюра(1914-1918) явилась фундаментальным вкладом в учение об адсорбции. Она позволяет учесть наиболее сильные отклонения от закона Генри, связанные с ограниченностью поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества.

Теория мономолекулярной адсорбции основывается на следующих положениях:

1) Адсорбция является локализованной (происходит на адсорбционных центрах).

2) Адсорбция происходит не на всей поверхности адсорбента, а на активных центрах, которыми являются выступы либо впадины на поверхности адсорбента. Активные центры считаются независимыми (т.е. один активный центр не влияет на адсорбционную способность других), и тождественными.

3) Каждый активный центр способен взаимодействовать только с одной молекулой адсорбата; в результате на поверхности может образоваться только один слой адсорбированных молекул.

4) Процесс адсорбции находится в динамическом равновесии с процессом десорбции.

На основании этих положений можно получить уравнение изотермы адсорбции. Скорость адсорбции из газовой фазы V _ад (т.е число молекул, адсорбированных за единицу времени) пропорциональна давлению газа и числу свободных центров на поверхности твердого тела. Если общее число центров a _∞ ,а при адсорбции оказывается занятыми a центров, то число центров, остающийся свободными равно ( a _∞ — a ). Поэтому:

Адсорбция динамически уравновешена процессом десорбции. Скорость десорбции пропорциональна числу адсорбированных молекул:

Переобозначаем k _ад / k _дес = b (где b –это константа адсорбированного равновесия),получаем

I — почти горизонтальный участок, который соответствует большим концентрациям, отвечает поверхности адсорбента, полностью насыщенным адсорбтивом. Величина удельной адсорбционной способности в этом случае не зависит от равновесной концентрации адсорбтива в растворе, что свидетельствует об образовании на поверхности мономолекулярного слоя.Описывается уравнением Генри:

II — соответствует промежуточным степеням заполнения поверхности.Описывается уравнением Фрейндлиха

III -почти все адсорбционные центры уже заняты и свободных центров на поверхности почти нет.

Уравнение Ленгмюра содержит два параметра, характеризующих адсорбцию. Это константа адсорбционного равновесия b и величина предельной адсорбции a _∞ , соответствующая полной полному заполнению поверхности мономолекулярным слоем адсорбата .

Для определения численных значений a _∞ и b уравнение Ленгмюра можно представить в виде:

С помощью линеаризации уравнения Ленгмюра можно определить предельную величину адсорбции a _∞ , соответствующую полному мономолекулярному покрытию адсорбента молекулами адсорбата.

Экспериментальное определение a _∞ позволяет рассчитать удельную поверхность адсорбента S _уд:

где N_A — постоянная Авагадро, W — площадь, приходящаяся на единичную молекулу адсорбата в мономолекулярном слое.

Однако,следует отметить некоторое развитие в положениях теории:

Во-первых,адсорбционные центры таки могут иметь разную энергию.

И в этом случае a _∞ будет рассчитываться как сумма всех различных центров:

Во-вторых,молекулы могут взаимодействовать между собой.

И наконец,на один адсорбционный центр может приходиться несколько молекул.

Т.е молекула первого слоя может являться вторичным центром.Это положение описывает теория о полимолекулярной адсорбции(теория БЭТ),но это уже совсем другая история 🙂

1.Левченко С.И. [Электронный ресурс] // Физическая и коллоидная химия.4.1.4Поверхностные явления и адсорбция.

2.Пальтиель Л.Р. [Электронный ресурс] // Коллоидная химия.8.Теория мономолекулярной адсорбции Ленгмюра

3. Журнал «Горизонт чистоты»[Электронный ресурс] //Теоретические основы клининга.2.5. Адсорбция ПАВ на границе раздела «жидкость-газ»

Видео:Уравнение ЛенгмюраСкачать

Физическая химия

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

§4. Мономолекулярная адсорбция. Изотерма адсорбции Ленгмюра

Чтобы получить теоретическую изотерму адсорбции, описывающую широкую область концентраций, необходимо использование представлений о механизме адсорбции и конкретных моделей.

Адсорбция рассматривается как квазихимическая реакция между адсорбатом и адсорбционными центрами поверхности адсорбента. В этом заключается основная идея адсорбционной теории Ленгмюра, которая явилась фундаментальным вкладом в учение об адсорбции. Ограниченность поверхности адсорбента приводит к её адсорбционному насыщению по мере увеличения концентрации распределяемого вещества. Это положение теории Ленгмюра уточняется следующими допущениями: 1) адсорбция локализована (молекулы не перемещаются по поверхности) на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбата; в результате образуется мономолекулярный слой; 2) адсорбционные центры энергетически эквивалентны – поверхность адсорбента эквипотенциальна; 3) адсорбированные молекулы не взаимодействуют друг с другом. 4) адсорбция обратима.

Для получения уравнения изотермы обратимся к основному положению теории Ленгмюра. Примем, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности:

↔

где – адсорбционные центры поверхности; В – распределяемое вещество; – комплекс, образующийся на поверхности.

По мере увеличения концентрации (давления) вещества В реакция сдвигается в сторону образования комплекса и свободных адсорбционных центров становится меньше. Константа адсорбционного равновесия равна

(IX.6)

В этом соотношении

(IX.7)

где А – величина адсорбции вещества В ; A  — емкость адсорбционного монослоя, или число адсорбционных центров, приходящихся на единицу площади поверхности (или на единицу массы адсорбента); А 0 – число оставшихся свободными адсорбционных центров, приходящихся на единицу площади поверхности (или на единицу массы адсорбента).

Подставляя уравнения (IX.7) в уравнение (IX.6), получим:

Опуская индекс при обозначении концентрации адсорбата С В , после простых преобразований окончательно имеем:

(IX.8)

Выражение (IX.8) называется уравнением изотермы мономолекулярной адсорбции Ленгмюра. Так как концентрации газов и паров практически пропорциональны парциальным давлениям, то для них изотерма адсорбции Ленгмюра принимает вид:

(IX.9)

Необходимо отметить, что константа адсорбционного равновесия в уравнении Ленгмюра характеризует энергию взаимодействия адсорбата с адсорбентом. Чем сильнее это взаимодействие, тем больше константа адсорбционного равновесия .

Адсорбционное уравнение Ленгмюра часто представляют относительно степени заполнения поверхности – отношения величины адсорбции А к емкости монослоя А 

(IX.10)

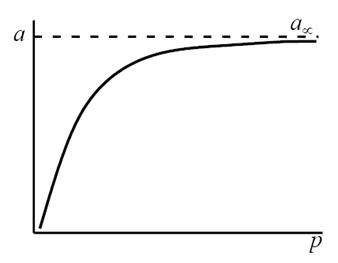
Типичная изотерма адсорбции Ленгмюра показана на рис.20.

Рис.20. Изотерма адсорбции Ленгмюра

Важны экстраполяционные следствия из соотношений (IX.8) – (IX.9). При малых концентрациях или давлениях, когда С  0, получаем:

и (IX.11)

Выражения (IX.11) соответствуют закону Генри: величина адсорбции линейно растет с увеличением концентрации.

При больших концентрациях и давлениях, когда КC >> 1 и KP >> 1, уравнения (IX.8) – (IX.9) переходят в соотношения:

и (IX.12)

Соотношения (IX.12) отвечают состоянию насыщения, когда вся поверхность адсорбента покрывается мономолекулярным слоем адсорбата. Экспериментальное определение А  позволяет рассчитать удельную поверхность адсорбента (поверхность единицы массы адсорбента):

(IX.12a)

где А  -предельная адсорбция, выражаемая числом молей адсорбата на единицу массы адсорбента; N A – число Авогадро; – площадь, занимаемая одной молекулой адсорбата.

Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помощью уравнения Ленгмюра, записанного в линейной форме (числитель (IX.8) переносят в знаменатель, а знаменатель – в числитель):

(IX.13)

Если обе части уравнения (IX.13) умножить на С, то получим ещё одну форму записи указанного уравнения, дающего линейную зависимость в координатах и С:

(IX.13а)

Такая линейная зависимость позволяет графически определить оба постоянных параметра ( А  и К ) адсорбционной изотермы. На рис.21 представлена типичная изотерма адсорбции в координатах уравнения (IХ.13а). Экстраполяция зависимости до оси ординат дает отрезок, равный 1/( А  K ), а тангенс угла наклона прямой к оси абсцисс равен 1/ А  ,

Рис.21. Изотерма адсорбции в координатах линейной формы уравнения Ленгмюра (IX.13а)

При адсорбции газов из их смесей в соответствии с уравнением изотермы Ленгмюра величины адсорбции суммируются, а концентрация свободных центров A 0 является общей для равновесной многокомпонентной системы.

Степень заполнения для i — o го компонента составит:

(IX.14),

где P i – парциальное давление i — o го компонента, а K i – его адсорбционная константа равновесия.

Из уравнения (IX.14) следует, что увеличение парциального давления одного компонента подавляет адсорбцию других, и тем сильнее, чем больше его адсорбционная константа равновесия.

Все рассмотренные до сих пор уравнения справедливы для мономолекулярной адсорбции, протекающей на адсорбенте с энергетически эквивалентными адсорбционными центрами. Однако реальные поверхности твердых тел, как правило, не обладают такими свойствами. Для приближения к реальным условиям целесообразно рассмотрение возможных распределений адсорбционных центров поверхности адсорбента по энергиям. Приняв экспоненциальное распределение адсорбционных центров по энергиям, в области средних заполнений получается найденное эмпирически уравнение Фрейндлиха :

(IX.15)

где К и п – постоянные.

Уравнение Фрейндлиха широко используется при обработке экспериментальных адсорбционных данных, в том числе в инженерных расчётах. Чаще всего оно применяется в логарифмической форме

позволяющей построить линейную зависимость ln A – ln P и графически определить оба постоянных параметра K и п.

§5 . Теория полимолекулярной адсорбции БЭТ

Уравнение Ленгмюра можно использовать только при условии, что адсорбция вещества сопровождается образованием мономолекулярного слоя. Это условие выполняется достаточно строго в случае хемосорбции, физической адсорбции газов при небольших давлениях и температурах выше критической (без конденсации на поверхности адсорбента), а также при адсорбции из растворов. Указанное ограничение для применения уравнения Ленгмюра связано не столько с формальным описанием адсорбции, сколько с невозможностью получить правильные значения параметров K и А  , соответствующих их физическому смыслу.

В большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и влияние поверхностных сил может распространяться на второй, третий и последующие адсорбционные слои. Эта возможность реализуется, когда газы и пары адсорбируются при температурах ниже критической. В этом случае образуются полимолекулярные слои вещества на поверхности адсорбента. Полимолекулярную адсорбцию можно представить как результат вынужденной конденсации пара под действием поверхностных сил. Если в области образования мономолекулярного слоя величина адсорбции существенно замедляет свой рост с увеличением давления пара, то в области давлений, близких к давлению насыщенного пара, она начинает резко возрастать и адсорбция заканчивается объёмной конденсацией пара при P =Р 0 (иногда используется обозначение P s ) (рис.22).

Рис.22 . Изотерма полимолекулярной адсорбции

Первые попытки получения уравнения изотермы полимолекулярной адсорбции были сделаны ещё Ленгмюром. Современная форма уравнения полимолекулярной адсорбции была предложена Брунауэром, Эмметом и Теллером. В соответствии с начальными буквами фамилий авторов обсуждаемая теория получила название теории БЭТ. В этой теории дополнительным допущением к тем, которые были положены в основу вывода уравнения изотермы Ленгмюра, является представление об образовании на поверхности адсорбента «последовательных комплексов» – адсорбционных центров с одной, двумя, тремя и т. д. молекулами адсорбата.

Величина адсорбции компонента В равна

(IX.16)

где С – константа уравнения, а P 0 – давление насыщенного пара компонента В при данной температуре.

Соотношение (IX.16) является основным уравнением обобщенной теории Ленгмюра и называется уравнением полимолекулярной адсорбции БЭТ. С уменьшением давления при P / P 0 1 уравнение БЭТ превращается в уравнение мономолекулярной адсорбции Ленгмюра, которое при дальнейшем уменьшении давления ( P  0) переходит в закон Генри.

При обработке экспериментальных результатов уравнение БЭТ обычно используют в линейной форме.

На теории БЭТ основан стандартный метод измерения удельной поверхности адсорбентов, катализаторов, порошков и других материалов (метод БЭТ). По экспериментальным данным находят величину A  , а затем по уравнению (IX.12a) рассчитывают удельную поверхность. В качестве адсорбатов используют инертные газы (азот, аргон, криптон и др.), которые проявляют слабое межмолекулярное взаимодействие на поверхности адсорбента, что находится в соответствии с исходными допущениями теории и обеспечивает достоверность получаемых результатов. Значения площади, занимаемой молекулой адсорбата в заполненном монослое принимают равной для азота 0,162 нм 2 , аргона – 0,138 нм 2 , криптона – 0,195 нм 2 . Для увеличения адсорбции таких газов ее ведут при низких температурах, откуда и частое название метода БЭТ – метод низкотемпературной адсорбции.

§6. Изотермы адсорбции и поверхностного натяжения растворов ПАВ
Уравнение Шишковского

Поверхностно-активные вещества (ПАВ), молекулы которых имеют дифильное строение и включают большой углеводородный радикал, отличаются высокой поверхностной активностью по отношению к воде, что отражает сильную зависимость поверхностного натяжения водного раствора ПАВ от их концентрации. Большие значения поверхностной активности предполагают пренебрежимо малые концентрации ПАВ в объеме раствора по сравнению с их концентрацией в поверхностном слое, т. е. с величиной их адсорбции на границе раствор – воздух. Подобная зависимость может обнаруживаться и в растворах других веществ на границе с жидкостью или твёрдым телом, например при специфическом взаимодействии с поверхностью. Отмеченная особенность позволяет пренебречь разницей между величиной адсорбции A и величиной гиббсовской адсорбции Г, т. е. будем полагать, что Г  A . Из этого соотношения следует, что для растворов ПАВ все уравнения адсорбции, включающие величину адсорбции A , будут также справедливы, если заменить А на Г.

Обратимся к уравнению изотермы адсорбции Лэнгмюра (IХ.8). Учитывая соотношение Г  A , величину адсорбции можно приравнять к её выражению из уравнения Гиббса (IX.3)

После разделения переменных имеем:

Проинтегрируем полученное выражение в пределах от 0 до С и от (поверхностное натяжение чистого растворителя) до :

так как Kd С= d (1 + K С ) .

После интегрирования получим уравнение Шишковского , характеризующее поверхностное натяжение растворов ПАВ в зависимости от концентрации:

(IX.17)

Подобную зависимость от С для ПАВ Б.А.Шишковский получил опытным путём в следующем виде:

, где a и b – константы.

Ленгмюр, связав уравнение Гиббса со своим уравнением, определил физический смысл констант эмпирического уравнения Шишковского. Одна из них ( a ) равна произведению A  RT , другая ( b ) имеет смысл константы адсорбционного равновесия K в уравнении Ленгмюра. Допущения, принятые при выводе уравнения Шишковского, показывают, что это уравнение в отличие от уравнений Гиббса и Ленгмюра справедливо только для поверхностно-активных веществ, обладающих высокой поверхностной активностью.

В соответствии с уравнением Шишковского при малых концентрациях ПАВ в растворе поверхностное натяжение снижается резко, но с ростом концентрации степень его снижения уменьшается и стремится к постоянному значению. Из вывода уравнения Шишковского следует, что такой ход зависимости от С обусловлен теми же причинами, что и снижение прироста адсорбции, а именно уменьшением концентрации свободных от ПАВ адсорбционных центров. Уравнение Шишковского, как и уравнение Ленгмюра, не учитывает взаимодействия молекул ПАВ на поверхности.

Дальнейшее увеличение концентрации ПАВ с большой поверхностной активностью может привести к появлению мицелл в растворе и на межфазной поверхности, что равнозначно возникновению новой фазы (механизм образования мицелл ПАВ рассматривается ниже), поэтому характер изменения величины адсорбции с увеличением концентрации ПАВ становится иным.

§7. Классификация и общая характеристика поверхностно-активных веществ. Правило Дюкло – Траубе

Наличие гидрофильной и олеофильной (гидрофобной) частей у молекул ПАВ является характерной отличительной особенностью их строения. По способности к диссоциации в водных растворах поверхностно-активные вещества делят на ионогенные и неионогенные. В свою очередь ионогенные ПАВ подразделяют на анионные, катионные и амфолитные (амфотерные).

Анионные ПАВ диссоциируют в воде с образованием поверхностно-активного аниона. К ПАВ этого типа, составляющего большую часть мирового производства всех поверхностно-активных веществ, относятся:

а) карбоновые кислоты и их соли (мыла) общей формулы RCOOM (где М – одновалентный металл), например пальмитат натрия C 15 H 31 COONa, стеарат натрия C 17 H 35 COONa, олеат натрия C 17 H 33 COONa;

б) алкилсульфаты ROSO 2 OM;

в) алкиларилсульфонаты RArSO 2 OM;

г) вещества, содержащие другие типы поверхностно-активных анионов, например фосфаты, тиосульфаты и т. д..

В кислых средах соли карбоновых кислот переходят в слабодиссоциированные и малорастворимые кислоты, а в присутствии некоторых катионов (кальция, магния) образуют нерастворимые соли, что резко снижает эффективность их действия как ПАВ, особенно ухудшает их моющее действие. Большими преимуществами в этом отношении обладают алкилсульфаты и алкилсульфонаты, которые являются солями сильных кислот и поэтому могут быть использованы в кислых и солевых растворах.

Катионные ПАВ диссоциируют в воде с образованием поверхностно-активного катиона. К катионным ПАВ относятся:

а) соли первичных, вторичных и третичных алифатических и ароматических аминов;

б) соли алкилзамещенных аммониевых оснований и т. д.

Катионные ПАВ – наиболее токсичные и наименее биологически разлагаемые из всех ПАВ; их часто используют в качестве бактерицидных, фунгицидных, дезинфицирующих веществ, ингибиторов коррозии.

Амфолитные ПАВ содержат две функциональные группы, одна из которых имеет кислый, а другая оснóвный характер, например карбоксильную и аминную группы. В зависимости от рН среды амфолитные ПАВ проявляют анионактивные или катионактивные свойства:

Неионогенные ПАВ не диссоциируют в растворах на ионы. Методы их получения основаны на реакции присоединения этиленоксида к спиртам, карбоновым кислотам, аминам и другим соединениям. Например, оксиэтилированные алкилспирты марки «ОС» синтезируют по реакции:

ROH + nH 2 C—CH 2  RO(CH 2 CH 2 O) n H

Полиоксиэтиленовая цепь определяет гидрофильные свойства неионогенных ПАВ. Изменяя длину полиоксиэтиленовой цепи, легко регулировать их коллоидно-химические свойства. Эти ПАВ применяются в любых средах (кислой и щелочной), а также в присутствии растворимых солей. Полиоксиэтиленовые эфиры алкилфенолов марки ОП обладают хорошими моющими свойствами.

К недостаткам этих ПАВ относится медленное разложение из-за наличия в их составе ароматического радикала и, как следствие, накопления их в объектах окружающей среды. Неионогенные ПАВ с алкильными радикалами способны биологически разлагаться достаточно полно и быстро.

Все дифильные поверхностно-активные вещества относительно поведения их в воде делят на истинно растворимые и коллоидные.

К первой группе относится большой класс растворимых в воде дифильных органических соединений с небольшим углеводородным радикалом, например низшие спирты, фенолы, кислоты и их соли, амины. Вещества этого типа в растворе находятся в молекулярно-дисперсном состоянии вплоть до концентраций, соответствующих их насыщенным растворам и разделению системы на две сплошные фазы. Эти вещества применяются в качестве смачивателей вспенивателей, гидрофобизаторов при флотации, диспергаторов, облегчающих процессы образования новых поверхностей, и т. д.

Особый интерес представляют коллоидные поверхностно-активные вещества. Именно они в первую очередь понимаются под термином ПАВ. Главной отличительной особенностью этих веществ является способность образовывать термодинамически устойчивые (лиофильные) гетерогенные дисперсные системы(ассоциативные или мицеллярные коллоиды). К основным свойствам коллоидных ПАВ, обусловливающим их широкое применение, относятся высокая поверхностная активность; способность к самопроизвольному мицеллообразованию – образованию лиофильных коллоидных растворов при концентрации ПАВ выше некоторого определенного значения, называемого критической концентрацией мицеллообразования (ККМ); способность к солюбилизации – резкому увеличению растворимости веществ в растворах коллоидных ПАВ вследствие их «внедрения» внутрь мицеллы; высокая способность стабилизировать различные дисперсные системы.

Поверхностная активность коллоидных ПАВ зависит, главным образом, от длины углеводородного радикала. Увеличение длины радикала на одну группу -СН 2 — приводит к возрастанию поверхностной активности приблизительно в 3,2 раза ( правило Дюкло – Траубе ). Это правило соблюдается в основном для истинно растворимых ПАВ.

Для органических сред правило Дюкло – Траубе обращается: поверхностная активность снижается с увеличением длины углеводородного радикала ПАВ.

В заключение можно отметить, что основной количественной характеристикой ПАВ является поверхностная активность, которая определяет их способность понижать поверхностное натяжение, вызывать эмульгирование, пенообразование, диспергирование и стабилизацию, смачивание и другие явления.