Гидродинамика — раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа.
Как и в других разделах физики сплошных сред, прежде всего осуществляется переход от реальной среды, состоящей из большого числа отдельных атомов или молекул, к абстрактной сплошной среде, для которой и записываются уравнения движения.
Идеальная среда
Гидродинамика изучает поведение идеальной жидкости — воображаемой среды без вязкости, сил трения и теплопроводности. Касательные напряжения равны нулю. Её можно представить, как систему небольших упругих шаров с пренебрежимо малым объёмом, не прилипающих друг к другу. Они часто сталкиваются друг с другом. Поэтому каждый шар переносит при движении массу, импульс, момент импульса, энергию.
Ламинарное и турбулентное движения жидкости
Экспериментально установлено, что в природе существуют два различных вида движения потока — ламинарное (слоистое, упорядоченное), при котором отдельные слои жидкости скользят друг относительно друга, и турбулентное (неупорядоченное), когда частицы жидкости движутся по сложным, все время изменяющимся траекториям.
Вследствие этого затрата энергии на турбулентное движение потока больше, чем на ламинарное.
Турбулентность — название такого состояния сплошной среды, газа, жидкости, их смесей, когда в них наблюдаются хаотические колебания мгновенных значений давления, скорости, температуры, плотности относительно некоторых средний значений, за счёт зарождения, взаимодействия и исчезновения в них вихревых движений различных масштабов. Происходит их нелинейное вихревое взаимодействие и распространение в пространстве и времени.
Турбулентность может возникать и при нарушении сплошности среды, например, при кавитации (кипении). При опрокидывании и разрушении волны прибоя возникает многофазная смесь воды, воздуха, пены. Мгновенные параметры среды становятся хаотичными.
Ламинарное течение
Отличие ламинарного течения от турбулентного состоит в характере и направлении водных (газовых) потоков. Они перемещаются слоями, не смешиваясь и без пульсаций. Другими словами, движение проходит равномерно, без беспорядочных скачков давления, направления и скорости.
Ламинарное течение жидкости образуется, например, в узких кровеносных сосудах живых существ, капиллярах растений и в сопоставимых условиях, при течении очень вязких жидкостей (мазута по трубопроводу). Чтобы наглядно увидеть струйный поток, достаточно немного приоткрыть водопроводный кран – вода будет течь спокойно, равномерно, не смешиваясь. Если краник отвернуть до конца, давление в системе повысится и течение приобретет хаотичный характер.
Движение жидкостей называется течением, а совокупность частиц движущейся жидкости — потоком. Графически движение жидкостей изображается с помощью линий тока. Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.
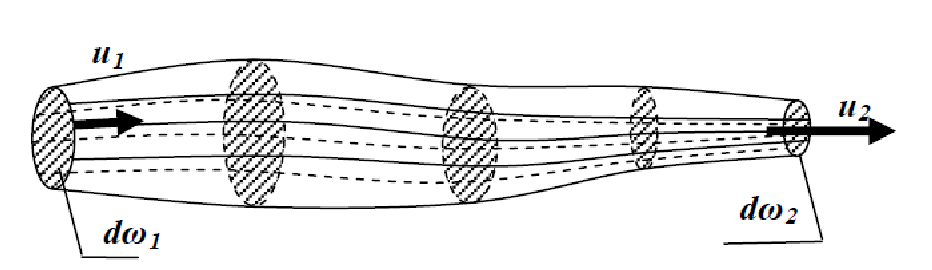
Трубка тока — трубчатая поверхность, ограниченная линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока, называется элементарной струйкой.
Для случая установившегося движения элементарной струйке придаются следующие свойства:
- форма элементарной струйки остается неизменной с течением времени;
- через стенки элементарной струйки движение жидкости не происходит (обмена энергией жидкости между элементарными струйками нет);
- вследствие малости поперечного сечения элементарной струйки скорость и гидродинамическое давление во всех точках ее поперечного сечения одинаковы.
Уравнение неразрывности жидкости
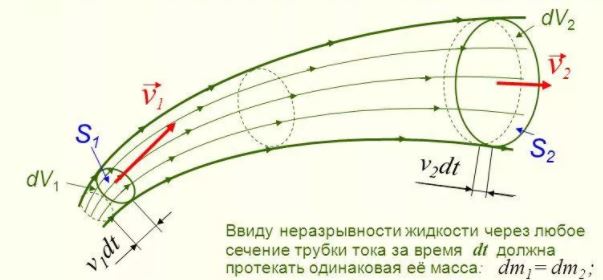
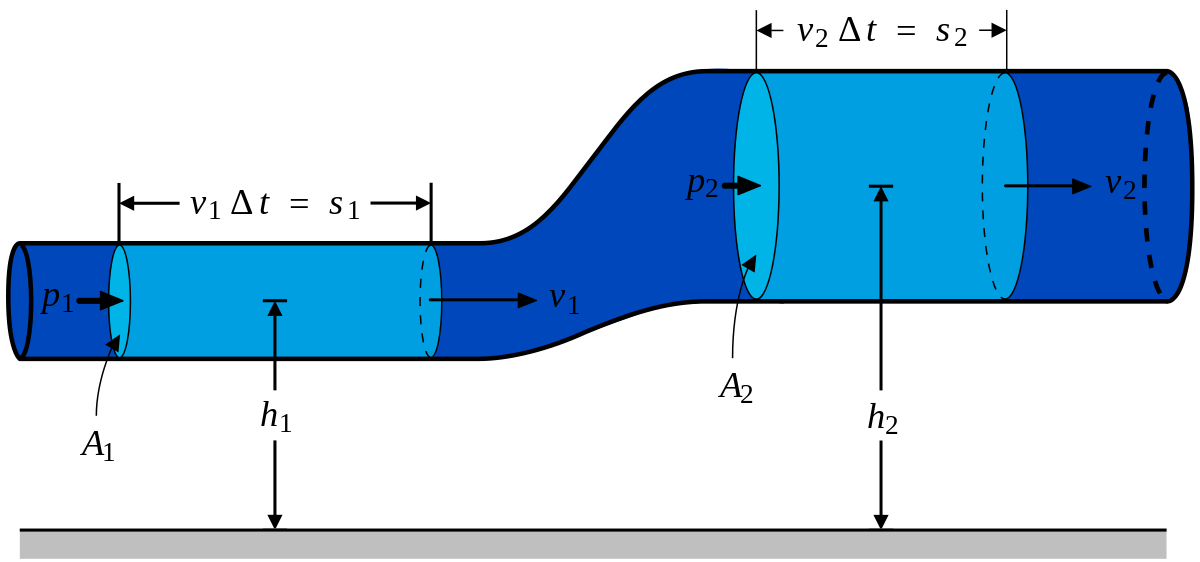
В гидравлике обычно рассматривают потоки, в которых не образуются разрывы. Если выделить в потоке два любых сечения, отстоящих друг от друга на некотором расстоянии, то за время Δ t через сечение S проходит объем жидкости SvΔ t; следовательно, за 1 с через S 1 пройдет объем жидкости S 1 v 1 , где v 1 — скорость течения жидкости в месте сечения S 1 . Через сечение S 2 за 1 с пройдет объем жидкости S 2 v 2 , где v 2 — скорость течения жидкости в месте сечения S 2 . Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (ρ = const), то через сечение S 2 пройдет такой же объем жидкости, как и через сечение S 1 , т. е.
Произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение называется уравнением неразрывности для несжимаемой жидкости.
Уравнение Бернулли
При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии.
Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости.
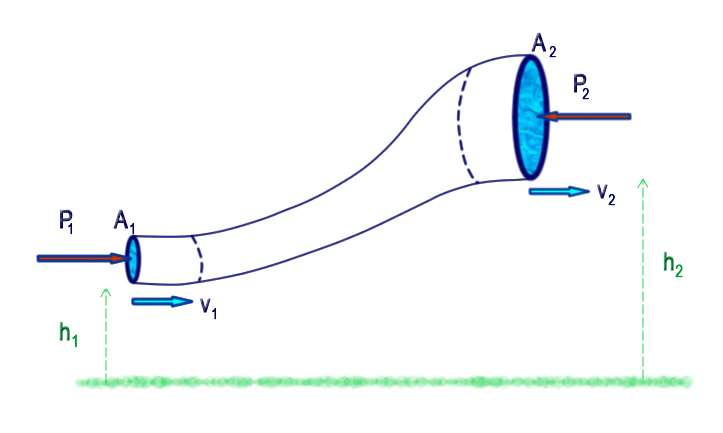
Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения. Различные части трубы могут находиться на разных высотах. У идеальной жидкости трение полностью отсутствует.
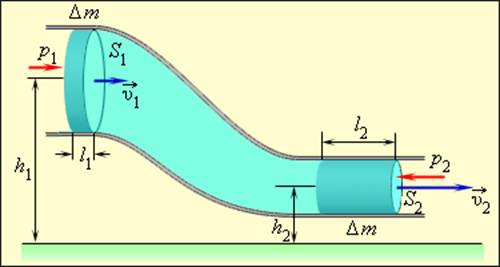
Выделим в стационарно текущей несжимаемой идеальной жидкости трубку тока, ограниченную сечениями S1 и S2, по которой жидкость течет слева направо. Пусть в месте сечения S1 скорость течения v1 давление р1 и высота, на которой это сечение расположено, h1. Аналогично, в месте сечения S2 скорость течения v2, давление р2, высота сечения h2. За малый промежуток времени Δt жидкость перемещается от сечения S1 к сечениюS‘1, от S2 к S’2.
Согласно закону сохранения энергии, изменение полной энергии Е2 — Е1 идеальной несжимаемой жидкости должно быть равно работе А внешних сил по перемещению массы т жидкости, где
— полные энергии жидкости массой т в местах сечений S1 и S2 соответственно.
С другой стороны, А — это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями S1 и S2, за рассматриваемый малый промежуток времени Δt:
где р — статическое давление (давление жидкости на поверхность обтекаемого ею тела),
ρv 2 /2 — динамическое давление.
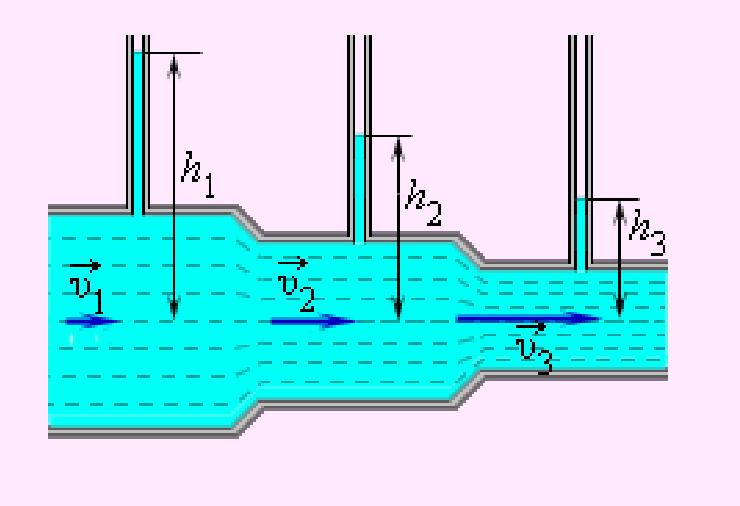
1. Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности следует, что при те чении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах, т. е. там, где скорость меньше.
Это можно продемонстрировать, установив вдоль трубы ряд манометров. В соответствии с уравнением Бернулли опыт показывает, что в манометрической трубке В, прикрепленной к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.
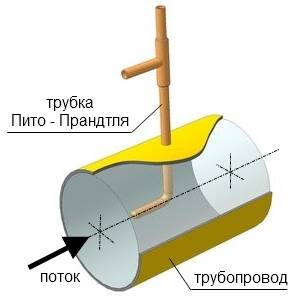
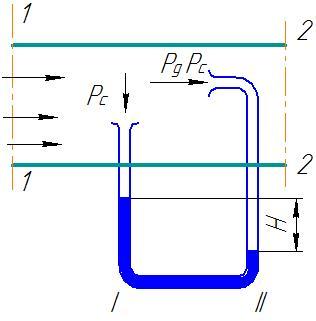
2. Так как динамическое давление связано со скоростью движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого применяется трубка Пито — Прандтля. Прибор состоит из двух изогнутых под прямым углом трубок, противоположные концы которых присоединены к манометру. С помощью одной из трубок измеряется полное давление (р0), с помощью другой — статическое (р).Манометром измеряется разность давлений:
где ρ — плотность жидкости в манометре. С другой стороны, согласно уравнению Бернулли, разность полного и статического давлений равна динамическому давлению:
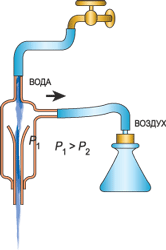
3. Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса. Струя воды подается в трубку, открытую в атмосферу, так что давление на выходе из трубки равно атмосферному. В трубке имеется сужение, по которому вода течет с большей скоростью. В этом месте давление меньше атмосферного. Это давление устанавливается и в откачанном сосуде, который связан с трубкой через разрыв, имеющийся в ее узкой части. Воздух увлекается вытекающей с большой скоростью водой из узкого конца. Таким образом можно откачивать воздух из сосуда до давления 100 мм рт. ст. (1 мм рт. ст. = 133,32 Па).
4. Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие.
Рассмотрим два сечения (на уровне h1 свободной поверхности жидкости в сосуде и на уровне h2 выхода ее из отверстия). Напишем для них уравнение Бернулли:
Так как давления р1 и р2 в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. p1 = p2 , то уравнение будет иметь вид
Из уравнения неразрывности следует, что v2/v1 = S1/S2, где S1 и S2 — площади поперечных сечений сосуда и отверстия. Если S1>>S2, то членом v 2 1/2 можно пренебречь и
Это выражение получило название формулы Торричелли .
Видео:Ламинарное и турбулентное течение жидкостей и газов. Уравнение неразрывности, уравнение БернуллиСкачать

Идеальная жидкость и уравнения, описывающие ее движение
Раздел физики, который изучает особенности движение жидких сред, называется гидродинамикой. Одним из главных математических выражений гидродинамики является уравнение Бернулли для идеальной жидкости. Именно этой теме посвящена статья.
Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Что такое идеальная жидкость?
Многие знают, что жидкая субстанция представляет собой такое агрегатное состояние материи, которое сохраняет при постоянных внешних условиях объем, но изменяет свою форму при малейшем воздействии на нее. Под идеальной жидкостью понимают такую текучую субстанцию, которая не имеет вязкости и является несжимаемой. Это два главных свойства, которые отличают ее от реальных текучих сред.

Отметим, что практически все реальные жидкости можно считать несжимаемыми, поскольку для небольшого изменения их объема необходимо огромное внешнее давление. Например, если создать давление в 5 атмосфер (500 кПа), то вода увеличит свою плотность всего на 0,024 %. Что касается вопроса вязкости, то для ряда практических задач, когда в качестве рабочей жидкости рассматривается вода, ею можно пренебречь. Для полноты информации отметим, что динамическая вязкость воды при 20 oC составляет 0,001 Па*с2, что в сравнении с этой величиной для меда (>2000), является мизерным значением.
Важно не путать понятия идеальной жидкости и идеального газа, поскольку последний является легко сжимаемым.
Видео:Режимы течения жидкости, ламинарный и турбулентный режимыСкачать

Уравнение непрерывности
В гидродинамике движение идеальной жидкости начинают рассматривать с изучения уравнения непрерывности ее потока. Чтобы понять суть вопроса, необходимо рассмотреть движение жидкости по трубе. Представим, что на входе труба имеет площадь сечения A1, а на выходе A2.
Теперь предположим, что жидкость течет в начале трубы со скоростью v1, это означает, что за время t через сечение A1 пройдет поток объемом V1 = A1*v1*t. Поскольку жидкость является идеальной, то есть несжимаемой, то точно такой же объем воды должен выйти из конца трубы за время t, получаем: V2 = A2*v2*t. Из равенства объемов V1 и V2 следует уравнение непрерывности потока идеальной жидкости:
Из полученного уравнения следует, что если A1>A2, то v1 должно быть меньше, чем v2. Другими словами, уменьшая сечение трубы, мы тем самым увеличиваем скорость выходящего из нее потока жидкости. Очевидно, что этот эффект наблюдал каждый человек в жизни, кто хотя бы раз поливал из шланга клумбы с цветами или огород, так, прикрывая пальцем отверстие шланга, можно наблюдать, как струя бьющей из него воды становится сильнее.
Видео:Галилео. Эксперимент. Закон БернуллиСкачать

Уравнение непрерывности для разветвленной трубы
Интересно рассмотреть случай движения идеальной жидкости по трубе, которая имеет не один, а два и более выхода, то есть является разветвленной. Например, площадь сечения трубы на входе равна A1, а к выходу она разветвляется на две трубы с сечениями A2 и A3. Определим скорости потоков v2 и v3, если известно, что на вход вода поступает со скоростью v1.
Используя уравнение непрерывности, получаем выражение: A1*v1 = A2*v2 + A3*v3. Чтобы решить это уравнения относительно неизвестных скоростей, нужно понимать, что на выходе, в какой бы трубе не находился поток, он движется с одинаковой скоростью, то есть v2=v3. Этот факт можно понять интуитивно. Если разделить некоторой перегородкой выходную трубу на две части, скорость потока при этом не изменится. Учитывая этот факт, получаем решение: v2 = v3 = A1*v1/(A2 + A3).
Видео:Закон БернуллиСкачать

Уравнение Бернулли для идеальной жидкости
Швейцарский физик и математик голландского происхождения Даниил Бернулли в своей работе «Гидродинамика» (1734 год) представил уравнение идеальной жидкости, описывающее ее движение. Оно записывается в следующей форме:
P+ ρ*v2/2 + ρ*g*h = const.
Это выражение отражает закон сохранения энергии в случае течения жидкости. Так, первое слагаемое (P) — давление, направленное вдоль вектора перемещения жидкости, которое описывает работу потока, второе слагаемое (ρ*v2/2) — это кинетическая энергия текучей субстанции, и третье слагаемое (ρ*g*h) — это ее потенциальная энергия.
Напомним, что это уравнение справедливо для идеальной жидкости. В действительности же всегда существует трение текучей субстанции о стенки трубы и внутри ее объема, поэтому в приведенное уравнение Бернулли вводят дополнительный член, описывающий эти энергетические потери.
Видео:Гидродинамика. Уравнение Бернулли. Физика 10 классСкачать

Использование уравнения Бернулли
Интересно привести некоторые изобретения, в которых используются выводы из уравнения Бернулли:
- Дымоход и вытяжки. Из уравнения следует, что чем больше скорость движения текучей субстанции, тем меньше ее давление. Скорость движения воздуха наверху дымохода больше, чем в его основании, поэтому поток дыма из-за разницы давлений всегда стремится вверх.
- Водопроводные трубы. Уравнение помогает понять, как изменится давление воды в трубе, если изменить диаметр последней.
- Самолеты и «Формула-1». Угол расположения крыльев самолета и антикрыла «Формулы-1» обеспечивает разность давления воздуха над и под крылом, что создает поднимающую и прижимающую силу соответственно.
Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Режимы течения жидкости
Уравнение Бернулли не учитывает режим движения жидкости, который может быть двух типов: ламинарный и турбулентный. Ламинарный поток характеризуется спокойным течением, при котором слои жидкости движутся по относительно плавным траекториям и не смешиваются между собой. Турбулентный режим движения жидкости характеризуется хаотичным перемещением каждой молекулы, составляющей поток. Особенностью турбулентного режима является наличие завихрений.
Каким способом будет течь жидкость, зависит от ряда факторов (особенности системы, например, наличия или отсутствия шероховатостей на внутренней поверхности трубы, вязкости субстанции и скорости ее перемещения). Переход между рассматриваемыми режимами движения описывается числами Рейнольдса.
Ярким примером ламинарного течения является медленное движение крови по гладким кровеносным сосудам. Пример турбулентного течения — сильный напор воды из крана.
Видео:Физика. 10 класс. Гидродинамика. Ламинарное и турбулентное течения жидкостей и газов /26.10.2020/Скачать

Ламинарное течение Турбулентное течение
ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ
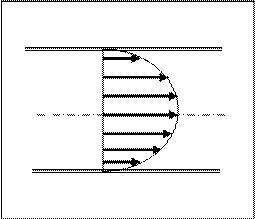
Наблюдается два вида течение жидкости (газа). В одних случаях жидкость как бы разделяется на слои, которые скользят друг относительно друга, не перемешиваясь. Такое течение называется л а м и н а р н ы м (слоистым). Если в ламинарный поток ввести подкрашенную струйку, то она сохраняется, не разрываясь, на всей длине потока, т.к. частицы жидкости в ламинарном потоке не переходят из одного слоя в другой. Ламинарное течение стационарно. При чем для него характерно то, что каждый слой движется с какой-то определенной скоростью υ. При небольших скоростях течения жидкости по трубе наблюдается ламинарное течение. Характер изменения скорости течения с расстоянием от оси трубы изображен на рис.4.7.
Ламинарное течение Турбулентное течение
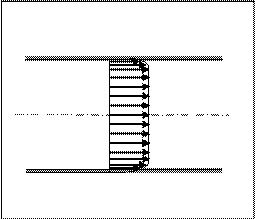
При увеличении скорости потока характер течения существенно изменяется. Возникает энергичное перемешивание жидкости, в результате чего внутри жидкости появляются вихри — турбулентности. Такое течение называется ту р б у л е н т н ы м. «Профиль» скоростей внутри турбулентного потока изображен на рис.4.8. Очевидно, что при турбулентном течении скорость в каждой точке сечения трубы приобретает некое значение. И только вблизи стенок скорость изменяется, при чем гораздо сильнее, чем при ламинарном течении, но в остальной части сечения скорость изменяется меньше.
Рассмотрим некоторые законы, выполняющиеся в ламинарном потоке жидкости (газа).
ЗАКОН БЕРНУЛЛИ
В ламинарном потоке жидкости (газа) вдоль любой линии тока выполняется следующее условие:
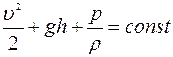
где υ – скорость течения жидкости (газа),
g = 9,8 м/с 2 – ускорение свободного падения в поле тяжести Земли,
h – ширина слоя жидкости (газа), движущегося со скоростью υ,
p – давление потока,
ρ – плотность жидкости (газа).
Эта формула называется уравнением Бернулли, а выше сказанное утверждение
законом Бернулли. Физический смысл закона Бернулли состоит в следующем: давление потока жидкости (газа) больше там, где скорость движения жидкости меньше. И обратно: давление меньше там, где скорость движения жидкости (газа) больше. Из чего это видно? Уравнение Бернулли содержит три слагаемых, сумма которых является постоянным числом. Т.е., если какое-то из слагаемых увеличится или уменьшится, то остальные должны измениться так, чтобы их сумма осталась прежней. Почти все величины, фигурирующие в уравнении Бернулли, являются постоянными параметрами. Изменяться может только скорость потока υ и давление потока р, причем обе эти величины стоят в числителях дробей. А это значит: если скорость будет увеличиваться, то давление должно уменьшиться так, чтобы значение суммы не изменилось. И наоборот: если уменьшится скорость, то давление увеличится.
Уравнению Бернулли можно также придать иной физический смысл, если произвести нехитрые математические преобразования:
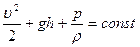

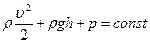
И тогда каждое слагаемое этого уравнения представляют собой давления, имеющие место в ламинарном потоке:
‒ так называемое динамическое давление потока (давление обусловленное кинетической энергией вещества потока – появляется при движении вещества)
- Сумма
‒ так называемое статическое давление потока (давление обусловленное потенциальной энергией вещества потока – появляется при нахождении вещества в состоянии покоя). Это давление складывается из двух составляющих:
◦ 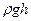
◦ 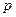
Таким образом уравнение Бернулли можно записать в следующем виде:
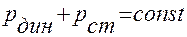
А закон Бернулли соответственно можно сформулировать следующим образом:
📸 Видео
Турбулентное течение круче ламинарного [Veritasium]Скачать
![Турбулентное течение круче ламинарного [Veritasium]](https://i.ytimg.com/vi/8tSbvSJT0eg/0.jpg)
Потери напора при движении жидкостиСкачать

Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Гидродинамика. Ламинарное и турбулентное течения жидкостей и газов.Скачать

Физика. 10 класс. ГидродинамикаСкачать

Уравнение Бернулли гидравликаСкачать

Урок гидравлики 16. Ламинарное и турбулентное течения Пограничный слойСкачать

Ламинарное и турбулентное теченияСкачать

Распределение давления в движущейся жидкости. Видеоурок 56. Физика 10 классСкачать

Ламинарное и турбулентное теченияСкачать

Парадокс сужающейся трубыСкачать

Закон Бернулли и движение по инерцииСкачать

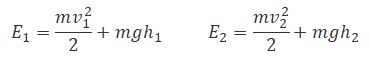
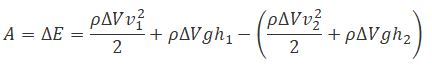
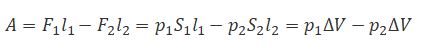
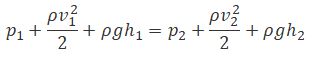
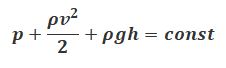
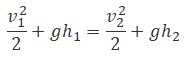
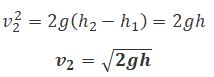




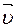
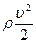 ‒ так называемое динамическое давление потока (давление обусловленное кинетической энергией вещества потока – появляется при движении вещества)
‒ так называемое динамическое давление потока (давление обусловленное кинетической энергией вещества потока – появляется при движении вещества)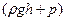 ‒ так называемое статическое давление потока (давление обусловленное потенциальной энергией вещества потока – появляется при нахождении вещества в состоянии покоя). Это давление складывается из двух составляющих:
‒ так называемое статическое давление потока (давление обусловленное потенциальной энергией вещества потока – появляется при нахождении вещества в состоянии покоя). Это давление складывается из двух составляющих: