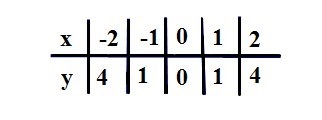Это старый и в настоящее время забытый способ решения квадратных уравнений.
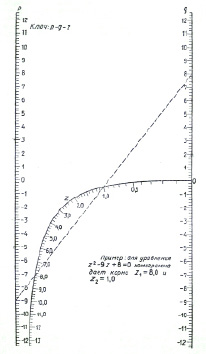
Номограмма даёт значения положительных корней уравнения z 2 + pz + q = 0. Если уравнение имеет корни разных знаков, то, найдя по номограмме положительный корень, отрицательный находят, вычитая положительный из – р.
Рис. 6. Вид монограммы для решения уравнения z 2 + pz + q = 0
В случае, когда оба корня отрицательны, берут z = – t и находят по номограмме два положительных корня t1; t 2 уравнения t 2 + – pt + z = 0, а затем z1 = – t1; z 2 = – t2.
Если коэффициенты p и q выходят за пределы шкал, выполняют подстановку z = kt и решают посредством номограммы уравнение
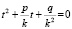
где k берётся с таким расчётом, чтобы имели место неравенства


Вид монограммы для решения уравнения z 2 + pz + q = 0 можно найти на рис. 6.
«Плюсы» и «минусы» различных способов решения
| Название способа решения квадратных уравнений | Плюсы | Минусы |
| Решение квадратных уравнений по формуле | Можно применить ко всем квадратным уравнениям. | Нужно выучить формулы. |
| Разложение левой части уравнения на множители | Дает возможность сразу увидеть корни уравнения. | Нужно правильно вычислить слагаемых для группировки. |
| Метод выделения полного квадрата | За минимальное количество действий можно найти корни уравнений | Нужно правильно найти все слагаемые для выделения полного квадрата. |
| Решение уравнений с использованием теоремы Виета | Достаточно легкий способ, дает возможность сразу увидеть корни уравнения. | легко находятся только целые корни. |
| Свойства коэффициентов квадратного уравнения | Не требует особых усилий | Подходит только к некоторым уравнениям |
| Решение уравнений способом переброски | За минимальное количество действий можно найти корни уравнения, применяется совместно со способом теоремы Виета. | легко найти только целые корни. |
| Геометрический способ решения квадратных уравнений | Наглядный способ. | похож на способ выделения полного квадрата |
| Графическое решение квадратного уравнения | Наглядный способ | Могут быть не точности при составлении графиков |
| Решение квадратных уравнений с помощью циркуля и линейки | Наглядный способ | Могут быть не точности |
| Решение квадратных уравнений с помощью номограммы | Наглядный способ, прост в применении. | Не всегда под рукой имеется номограмма. |
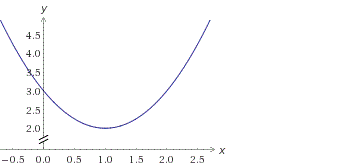
График квадратичной функции.
•Квадратичной функцией называется функция вида y=ax 2 +bx+c, где a,b,c — числа, причем a≠0.
•Графиком квадратичной функции является парабола.
Чтобы построить график функции y=x 2 составим таблицу значений
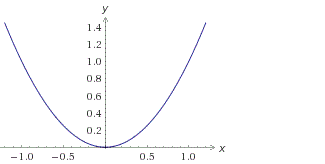
и построим график, используя полученные точки:
Внимание! Если в уравнении квадратичной функции старший коэффициент a=1, то график квадратичной функции имеет ровно такую же форму, как график функции y=x 2 при любых значениях остальных коэффициентов.
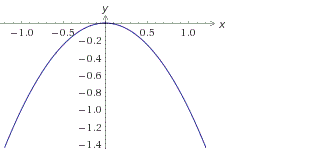
График функции y=-x 2 имеет вид:

Итак:
•Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
•Если старший коэффициент a 2 +bx+c нужно решить квадратное уравнение ax 2 +bx+c=0.
В процессе решения квадратного уравнения мы находим дискриминант: D=b 2 -4ac, который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1. Если D 2 +bx+c=0 не имеет решений, и, следовательно, парабола y=ax 2 +bx+c не имеет точек пересечения с осью ОХ.
Если a>0,то график функции выглядит примерно так:
2. Если D=0 ,то уравнение ax 2 +bx+c=0 имеет одно решение, и, следовательно, парабола y=ax 2 +bx+c имеет одну точку пересечения с осью ОХ.
Если a>0,то график функции выглядит примерно так:
3.Если D>0, то уравнение ax 2 +bx+c=0 имеет два решения, и, следовательно, парабола y=ax 2 +bx+c имеет две точки пересечения с осью ОХ: 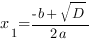

Если a>0, то график функции выглядит примерно так:
Значит, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.
Следующий важный этап построения графика квадратичной функции – координаты вершины параболы:
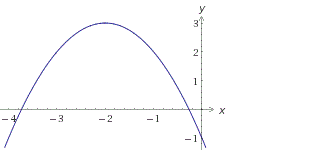
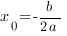

Прямая, прохдящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один этап построения графика функции – точка пересечения параболы y=ax 2 +bx+c с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы y=ax 2 +bx+c с осью OY, нужно в уравнение параболы вместо х подставить ноль: y(0)=c.
- Тема: «Решение квадратных уравнений с помощью номограммы»
- Разработка теории номографических построений началась в 19 в. Первой была создана теория построения прямолинейных сетчатых номограмм (французский математик Л. , 1843).
- Основания общей теории номографических построений дал М. Окань в 1884—91; в его же работах впервые встречается название Номография. Первым в России вопросами Номография начал заниматься М. Герсеванов в 1906—08. Большая заслуга в деле развития теории Номография и организации номографирования инженерных расчетов принадлежит А. Глаголеву, возглавлявшему советскую номографическую школу.
- Номограмма (от греческого «nomos» – закон и …грамма), графическое представление функции от нескольких переменных, позволяющее с помощью простых геометрических операций (например, прикладывание линейки) исследовать функциональные зависимости без вычислений. Например, решать квадратное уравнение без применения формул.
- Геометрические изображения зависимостей между переменными, избавляющие от вычислений, известны давно. К ним можно отнести достаточно сложные построения, содержащие семейства линий и шкалы как изображения переменных (встречающиеся, например, в солнечных часах и астролябиях).
- Номография (от греч. nómos — закон и . графия), раздел математики, объединяющий теорию и практические методы построения номограмм – специальных чертежей, являющихся изображениями функциональных зависимостей. Особенность номограмм заключается в том, что каждый чертеж изображает заданную область изменения переменных и каждое из значений переменных в этой области изображено на номограмме определенным геометрическим элементом (точкой или линией); изображения значения переменных, связанных функциональной зависимостью, находятся на номограмме в определенном соответствии, общем для номограмм одного и того же типа
- (Современный энциклопедический словарь)
- Квадратные уравнения с помощью номограммы
- 💥 Видео
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Тема: «Решение квадратных уравнений с помощью номограммы»
Тема: «Решение квадратных уравнений с помощью номограммы»
Тип занятия: Изучение нового материала
Вид занятия: Урок углубления знаний
Программное обеспечение: Авторская программа элективного курса ««История квадратных уравнений и десять способов их решения»
Дидактический материал: Номограммы для учащихся, карточки с заданиями
Форма работы: индивидуальная, парная, групповая
Время проведения: 40 минут
— Формирование знания решения квадратных уравнений с помощью номограмм
· Познакомить с теорией способа решения квадратных уравнений с помощью номограмм
· Познакомить с применением способа решения квадратных уравнений с помощью номограмм на практике
· Создать условия для формирования мотивации выбора математики для последующего углубленного изучения.
· Выработать умения выбирать рациональный способ решения квадратных уравнений и создать условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений.
· Сформировать умения составлять алгоритмы для способа решения квадратных уравнений
· Развитие вычислительных навыков
· Развитие кругозора учащихся
· Развитие умения наблюдать, анализировать.
· Способствовать интеллектуальному развитию учащихся, формированию качеств мышления, познавательных интересов, творческих способностей учащихся.
· Развитие коммуникативных качеств личности
· Воспитание навыков сотрудничества в процессе совместной работы.
· Содействовать воспитанию интереса к математике, активности, мобильности, отношения ответственной зависимости, взаимопомощи, умения общаться, толерантности у детей
· Воспитание самостоятельности, умения представлять выбранный способ решения уравнения
— Организационный момент. Вступительное слово учителя
— Актуализация опорных теоретических и практических знаний о способах решения квадратных уравнений
— Объяснение нового материала
— Закрепление нового материала
— Подведение итогов. Рефлексия.
Вступительное слово учителя.
Сообщаю цель, задачи занятия, план работы на занятии.
Актуализация опорных теоретических – повторение алгоритмов известных способов решения квадратных уравнений (разложение левой части на множители, выделение квадрата двучлена, с помощью теоремы Виета, с помощью свойства коэффициентов, с помощью «переброски» коэффициентов, графический способ)
Актуализация практических знаний о способах решения квадратных уравнений. Решить квадратные уравнения различными способами:
1. Способом разложения на множители
2. Способом выделения квадрата двучлена
3. По теореме Виета (обратной)
4. Используя свойства коэффициентов
345х2 – 137х – 208 = 0
5. Используя свойства коэффициентов
313х2 + 326х + 13 = 0
6. Способом переброски
7. Графическим способом
Задание выполняют самостоятельно, но каждое уравнение решает двое учащихся, которые не в одной группе.
Проверка проводится по группам учащихся с одинаковыми заданиями.
1) Способом разложения на множители:
7х2 + 7х + 2х + 2 = 0
7х (х + 1) + 2(х +1) =0
7х +2 = 0 или х +1 = 0
2) Способом выделения квадрата двучлена:
3(х2 + 2/3 х –5/3) = 0
х2 + 2* 1/3 х +1/9– 1/9– 5/3=0
(х +1/3)
(х + 1/3)
х +1/3 = 4/3 или х+1/3 = –4/3
3) По теореме Виета (обратной)




х 


4) Используя свойство коэффициентов
345х2 – 137х – 208 = 0
а + b+ с = 345 –137 –208 =0, значит, х 

5) Используя свойство коэффициентов
313х2 + 326х + 13 = 0
а – b +с = 313 – 326 +13 = 0, значит, х 

6) Способом переброски


у 

у 

у

х 


7) Графическим способом х2 – 2х – 3 = 0
у = х2 , графиком является парабола
у = 2х + 3, графиком является прямая
Прямая и парабола
имеют две общие точки,
абсциссы которых являются
Объяснение нового материала
«Решение квадратных уравнений с помощью номограммы»
Сообщение ученика о понятии номограмма
Видео:Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать

Разработка теории номографических построений началась в 19 в. Первой была создана теория построения прямолинейных сетчатых номограмм (французский математик Л. , 1843).
Видео:Быстрый способ решения квадратного уравненияСкачать

Основания общей теории номографических построений дал М. Окань в 1884—91; в его же работах впервые встречается название Номография. Первым в России вопросами Номография начал заниматься М. Герсеванов в 1906—08. Большая заслуга в деле развития теории Номография и организации номографирования инженерных расчетов принадлежит А. Глаголеву, возглавлявшему советскую номографическую школу.
Видео:Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

Номограмма (от греческого «nomos» – закон и …грамма), графическое представление функции от нескольких переменных, позволяющее с помощью простых геометрических операций (например, прикладывание линейки) исследовать функциональные зависимости без вычислений. Например, решать квадратное уравнение без применения формул.
(Большой энциклопедический словарь: Номограмма – см. в ст. Номография.)
Номограмма – графическое изображение математической зависимости. С помощью номограммы можно, не производя вычислений, получать решения уравнений, для которых номограмма построена. Номограммы широко применяются в базисных прицелах, радиотехнических системах и других устройствах и системах для бомбометания, воздушной стрельбы, самолетовождения и т. д.
(Военно-авиационный словарь, Москва, Воениздат)
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Геометрические изображения зависимостей между переменными, избавляющие от вычислений, известны давно. К ним можно отнести достаточно сложные построения, содержащие семейства линий и шкалы как изображения переменных (встречающиеся, например, в солнечных часах и астролябиях).
Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Номография (от греч. nómos — закон и . графия), раздел математики, объединяющий теорию и практические методы построения номограмм – специальных чертежей, являющихся изображениями функциональных зависимостей. Особенность номограмм заключается в том, что каждый чертеж изображает заданную область изменения переменных и каждое из значений переменных в этой области изображено на номограмме определенным геометрическим элементом (точкой или линией); изображения значения переменных, связанных функциональной зависимостью, находятся на номограмме в определенном соответствии, общем для номограмм одного и того же типа
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

(Современный энциклопедический словарь)
Это старый и незаслуженно забытый способ решения квадратных уравнений, о котором рассказывается в Таблице XXII Четырехзначных математических таблиц, автор Брадис для решения уравнения z2 + рz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения. Криволинейная шкала номограммы построена по формулам ОВ = 

(слайд) Полагая, что ОС = р, ЕД =q, ОЕ = а, из подобия треугольников САН и СДF (почему треугольники подобны?) получим пропорцию 





p – q = p + pz +z
z
Из пропорции после подстановок и упрощений получаем уравнение z2 + рz + q = 0, причем буква z означает метку любой точки криволинейной шкалы.
 |
 |