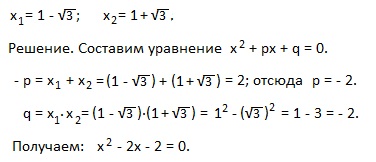Квадратное уравнение х2 рх q 0 имеет два различных натуральных корня (3 видео)

Содержание

Докажите, что если q
Ваш ответ
решение вопроса
Похожие вопросы
math4school.ru
Квадратный трёхчлен
Немного теории
Задачи с решениями
Задачи без решений
Итоговая работа по теме: «Многоуровневая система задач с параметрами по теме «Квадратные уравнения» в курсе алгебры 8 класса»
8.2.3. Теорема Виета
🎥 Видео

Видео:Уравнение x^2+px+q=0 имеет корни -6; 4. Найдите q. | ОГЭ 2017 | ЗАДАНИЕ 4 | ШКОЛА ПИФАГОРАСкачать

Докажите, что если q

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Ваш ответ

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

решение вопроса

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

math4school.ru

Видео:Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать

Квадратный трёхчлен

Немного теории

В большинстве задач, сводящихся к исследованию квадратичной функции

полезно представить себе её график:

если он пересекает ось Ох в двух точках (корнях) х₁ и х₂, то между корнями значения функции у = f(х) противоположны по знаку числу а, а вне отрезка [х₁; х₂] – совпадают по знаку с числом а;
при этом вершина параболы у = f(х) (абсцисса которой равна полусумме корней) соответствует точке экстремума функции у = f(х): минимума, если а > 0, и максимума, если а

В ряде задач полезно использовать такой факт:

если непрерывная на отрезке [а, b] функция у = f(х) принимает в концах этого отрезка значения разных знаков, то между точками a и b лежит хотя бы один корень уравнения f(х) = 0.

Задачи с решениями

1. Известно, что a + b + c 2 + bx + c = 0 не имеет действительных корней. Определить знак коэффициента с.

Квадратный трёхчлен f(x) = ax 2 + bx + c не имеет действительных корней, значит, он сохраняет один и тот же знак для всех значений аргумента х. Так как f(1) = a + b + c

2. Может ли квадратное уравнение ax 2 + bx + c = 0 с целыми коэффициентами иметь дискриминант равный 23?

Допустим, что дискриминант указанного уравнения равен числу 23. Тогда можно записать:

Заметим, что b – 5 и b + 5 – числа одинаковой чётности, поэтому их произведение, если оно чётно, делится на 4. Правая часть последнего равенства есть чётное число, не делящееся на 4. Полученно противоречие, значит, сделаное допущение ложно.

3. Найти все пары действительных чисел p, q, для которых многочлен x 4 + px 2 + q, имеет 4 действительных корня, образующих арифметическую прогрессию.

Многочлен x 4 + px 2 + q, имеет 4 действительных корня в том и только в том случае, если многочлен у 2 + pу + q (относительно у = x 2 ) имеет два неотрицательных корня, т.е. числа р и q удовлетворяют условиям

Если исходный многочлен имеет 4 действительных корня (а именно: –х₁, –х₂, х₁, х₂, где без ограничения общности считаем, что х₁ > х₂ > 0), то они образуют арифметическую прогрессию тогда и только тогда, когда совместна система

(смотрите теорему Виета и обратную к ней), т.е. когда q = 0,09 · р 2 . Таким образом, все искомые пары чисел р, q описываются условиями

(неравенства p 2 > 4q и q > 0,вытекают из последнего равенства).

4. Пусть a, b, c – действительные числа. Доказать, что уравнение

всегда имеет хотя бы один действительный корень. Выяснить, когда таких корня два.

Без ограничения общности рассуждений можно считать, что a b c. Рассмотрим все возможные случаи:

f ( a ) = ( a – b ) ( a – c ) > 0,

f ( c ) = ( c – a ) ( c – b ) > 0.

Так как f ( x ) – непрерывная квадратичная функция, принимающая значения разного знака на концах интервалов (a; b) и (b; c), то она имеет два различных действительных корня х 1 и х 2 . Более того

Решение задачи окончено.

5. Дан многочлен ax 2 + bx + c. За один ход разрешается заменить х на (х – k) или заменить многочлен целиком на многочлен

Можно ли после нескольких ходов из многочлена x 2 – 3x – 4 получить многочлен x 2 – 2x – 5?

Нетрудно убедиться, что при указанных заменах исходного многочлена его дискриминант не изменяется. Значит, если из многочлена x 2 – 3x – 4 можно получить многочлен x 2 – 2x – 5, то их дискриминанты должны быть равны. Однако это не так.

6. Найдите все значения a и b, такие, что для любого х из отрезка [–1; 1] будет выполняться неравенство

Пусть числа а и b такие, что для любого х из отрезка [–1; 1] выполняется данное неравенство, т. е,

Полагая здесь последовательно х = 0, х = 1, х = – 1, получаем, что а и b удовлетворяют следующей системе неравенств:

Сложив почленно два последних неравенства, подучим

Отсюда и из первого неравенства следует, что b = –1. Тогда а удовлетворяет следующим двум неравенствам:

и поэтому, а = 0. Таким образом, если существуют числа а и b, удовлетворяющие условию задачи, то

и других решений задача не имеет.

Чтобы доказать, что найденные значения а = 0, b = – 1 являются решением задачи, остается проверить, что для любого х из отрезка [–1; 1] верно двойное неравенство

А оно равносильно неравенству

которое, очевидно, справедливо на числовом промежутке [–1; 1].

7. По трём прямолинейным дорогам с постоянными скоростями идут три пешехода. В начальный момент времени они не находились на одной прямой. Докажите, что они могут оказаться на одной прямой не более двух раз.

Поставим каждому из пешеходов в соответствие точку в прямоугольной системе координат. Точки (х₁; у₁), (х₂; у₂), (х₃; у₃) лежат на одной прямой тогда и только тогда, когда

Так как скорости пешеходов постоянны, то х₁(t), у₁(t), х₂ (t), у₂(t), х₃(t) и у₃(t) – линейные функции от времени t и последнее равенство является квадратным уравнением относительно t, которое может иметь не более двух решений t₁ и t₂. Это и есть те два возможных момента времени, когда все три пешехода могут оказаться на одной прямой.

8. На координатной плоскости Oхy нарисован график функции y = x 2 . Потом оси координат стёрли, осталась только парабола. Как при помощи циркуля и линейки восстановить оси координат и единицу длины?

Докажем следующую лемму.

Лемма. Пусть M и N – середины двух параллельных хорд параболы. Тогда прямая MN параллельна оси параболы.

Доказательство. Пусть хорды AB и CD параболы лежат на параллельных прямых

тогда абсциссы точек A , B , C , D – это корни уравнений

а абсциссы точек M и N – полусуммы корней этих уравнений, то есть по теореме Виета равны k /2. Следовательно, точки M и N лежат на прямой х = k /2, которая параллельна оси Oy . Лемма доказана.

Вернёмся к исходной задаче.

Последовательно осуществляем следующие построения:

1) две параллельные прямые, каждая из которых пересекает параболу в двух точках;

2) прямую через середины получающихся отрезков;

3) перпендикуляр к этой прямой, пересекающий параболу в двух точках А и В;

4) серединный перпендикуляр к отрезку АВ – это ось Оу;

5) ось Ох перпендикулярна Оу в точке пересечения с параболой;

6) единичный отрезок – абсцисса пересечения прямой у = х с параболой.

9. Учитель написал на доске квадратный трехчлен х 2 + 10х + 20, после чего по очереди каждый из учеников увеличил или уменьшил на единицу либо коэффициент при х, либо свободный член, но не оба сразу. В результате на доске оказался написан квадратный трехчлен х 2 + 20х+10. Верно ли, что в некоторый момент на доске был написан квадратный трехчлен с целыми корнями?

Заметим, что при каждом изменении трехчлена его значение в точке х = – 1 изменяется на 1 (в ту или другую сторону). Значение первого трехчлена

в этой точке равно f(–1) = 11, а последнего,

— g(–1) = –9. Поэтому в какой-то промежуточный момент на доске был написан трехчлен

для которого h(–1)=0. Оба его корня – целые числа: один равен –1, другой по теореме Виета равен –q.

Каждому квадратному трёхчлену

поставим в соответствие точку координатной плоскости Оbc, где вдоль оси Оb будем откладывать значения второго коэффициента, а вдоль Ос – свободного члена. Многочленам

будут соответствовать точки

соответственно. Предложенные в условии операции предполагают перемещение от точки А к точке В вдоль узлов некоторой ломаной L. Узлы L – некоторые целочисленные точки плоскости Оbc, а длина каждого звена L равна 1 (соседние звенья могут лежать на одной прямой).

Так как точки А и В расположены в разных полуплоскостях относительно прямой

то ломаная L одним из своих узлов имеет точку этой прямой. Значит, одним из промежуточных многочленов будет многочлен вида

10. Какова вероятность того, что корни квадратного уравнения x 2 + 2bx + c = 0 действительны?

Для того чтобы вопрос задачи имел смысл, предположим, что точка (b; c) равномерно распределена на квадрате с центром в начале координат и стороной 2B. Решим задачу при фиксированном значении B, а затем устремим B к бесконечности, так что b и c могут принимать любые значения.

На рисунке более тёмная выделенная область отвечает случаю действительных корней,

более светлая – комплексных.

Для того чтобы уравнение имело действительные корни, необходимо и достаточно, чтобы

На приведенном рисунке изображена парабола с = b 2 и показана область, где наше уравнение имеет действительные корни для B = 4.

Нетрудно подсчитать, что площадь «комплексной» области равна (4 · B 3/2 )/3 (при B > 1), а площадь всего квадрата, конечно, равна 4B 2 . Следовательно, вероятность того, что корни комплексные, равна 1/(3 √ В ). При B = 4 она составляет 1/6. Действительно,

(4 · B 3/2 ) / 3	=	1	=	1
4 B 2	=	3 · √ В	=	3 · √ 4

С ростом B значение дроби 1/ √ В стремится к нулю, так что вероятность того, что корни вещественные, стремится к 1.

Замечание. Рассмотренная задача отличается от такой же задачи, связанной с уравнением

Конечно, можно разделить на a, но если a, b и c были независимы и равномерно распределены в некотором кубе, то b/a и c/a уже зависимы и распределены неравномерно.

Задачи без решений

1. Корни уравнения х 2 + pх + q = 0, у которого p + q = 198, являются целыми числами. Найдите эти корни.

2. В квадратном уравнении х 2 + pх + q = 0 коэффициенты p и q независимо пробегают все значения от –1 до +1 включительно. Найти множество значений, которые при этом могут принимать действительные корни данного уравнения.

3. Квадратный трёхчлен f ( х ) = ax 2 + bx + c таков, что уравнение f ( х ) = x не имеет действительных корней. Докажите, что уравнение f ( f ( х )) = х так же не имеет вещественных корней.

4. Найдите уравнение общей касательной к параболам у = x 2 + 4x + 8 и у = x 2 + 8x + 4.

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Итоговая работа по теме: «Многоуровневая система задач с параметрами по теме «Квадратные уравнения» в курсе алгебры 8 класса»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

Видеолекции для
профессионалов

Свидетельства для портфолио
Вечный доступ за 120 рублей
311 видеолекции для каждого

Уточкина Татьяна Анатольевна

Государственное бюджетное общеобразовательное учреждение Самарской области г. о. Отрадный средняя общеобразовательная школа № 8

А. Г. Мордкович Алгебра 8 класс: Учебник для общеобразовательных учреждений – М.: Мнемозина, 2010.

Задачи с параметрами практически не представлены в школьном курсе математики. Между тем они включены в итоговую аттестацию как в 9, так и в 11 классах. Для решения задач с параметрами не требуется обладать знаниями, выходящими за рамки школьной программы. Однако непривычность формулировки обычно ставит в тупик учащихся, не имеющих опыта решения подобных задач.

Параметр, присутствующий в условии задач, не создаёт слишком больших трудностей, но, в то же время, позволяет сформировать у учащих-ся отчетливое представление о параметрических задачах и основных прин-ципах их решения.

сформировать у учащихся отчетливое представление о параметрических задачах при решении квадратных уравнений и основных принципах их решения.

— образовательные (формирование познавательных УУД):

анализировать и выявлять существенную информацию, самостоятельное выделение и формулирование познавательной цели, моделировать условие в графическом виде, переформулировать условие, строить логическую цепочку рассуждений, критически оценивать полученный ответ, осознанное и произвольное построение речевого высказывания, выбор наиболее эффективного способа решения задач, постановка и формулирование проблемы, выдвижение гипотез и их обоснование;

— развивающие (формирование регулятивных УУД)

целеполагание, планирование своей деятельности в зависимости от конкретных условий;

прогнозирование способа её решений, контроль и оценка процесса и результатов деятельности, волевая саморегуляция, готовность к саморазвитию, самообразованию;

— воспитательные (формирование коммуникативных и личностных УУД):

смыслообразование, умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем.

На каждом этапе решения задач с параметром формируются универсальные учебные действия.

Этапы решения задачи

Целеполагание, выделение существенной информации, прогнозирование способа решения, аналогия, классификация, знакосимволические действия.

Схематическая запись условия

Планирование, систематизация, моделирование.

Составление математической модели

Корректировка условия, моделирование в графическом виде, создание способа решения задачи.

Решение математической модели

Анализ и выявление существенной информации, выделение следствий, построение цепи рассуждений, выдвижение и проверка гипотезы, преобразования модели.

Анализ, выделение следствий, конкретизация.

Поиск аналогов, умение передать содержание, создание способов решения проблем, умение применять схемы, анализ и синтез.

Самооценка, самоанализ, готовность к саморазвитию, умение определить цели, ставить и формулировать для себя новые задачи, развивать мотивы и интересы своей познавательной деятельности.

Ниже приводится многоуровневая система задач по решению и исследованию квадратных уравнений с параметрами в курсе алгебры 8 класса. Данная система задач включает в себя задачи трёх уровней: базовые, модифицированные и исследовательские.

Задачи первого уровня (базовые) позволяют сформировать у учащихся ключевые компетенции, применимые в учебной деятельности при решении задач более высокого уровня.

Видоизменение задач второго уровня (модифицированных) осуществляется в трёх направлениях: увеличение технической сложности и трудности задачи; варьирование известного алгоритма решения; необычная форма предоставления условия задачи, при которой сразу не видно применение знакомого способа действий.

При решении задач третьего уровня учебная деятельность носит исследовательский характер. При решении таких задач ученик должен ориентироваться в новой ситуации и выработать новые приемы действий.

1. Линейным или квадратным является уравнение

b ( b -5) x 2 +(6 b -3) x -18= 0 относительно х при:

2. При каких значениях параметра p уравнение х 2 -2( p +3)х+16=0 имеет:

в) не имеет действительных корней?

3. При каких значениях параметра p уравнение 2х 2 + p х+68=0 имеет корень, равный 17?

4. Найдите p и q , если х₁=1 и х₂=2 – нули квадратичной функции

Т. к. х₁=1 и х₂=2 – нули квадратичной функции у=х 2 + p х+ q , то по теореме Виета имеем: х₁+ х₂=- p , х₁∙х₂= q . Тогда p =-3, q =2.

5. Решите относительно х уравнение

, D = 4 – 4с

Алгоритм: рассмотреть случаи, когда: D > 0, D = 0, D

3) с > 1 исходное уравнение корней не имеет.

Ответ: если с  (–  ; 1), то _,;

если с  (1; +  ), то корней нет.

6. Докажите, что не существует такого значения k , при котором уравнение имеет только один корень.

Уравнение имеет один корень, если дискриминант равен 0.

Если это уравнение не имеет решений, значит, и не может иметь только одного решения.

, D

7. При каких значениях параметра b уравнение имеет: а) два положительных корня;

б) два отрицательных корня;

в) единственный корень?

Если b  1, то

Согласно теореме Виета: а) , b  (–  ; – 1)  ( – 1; +  );

б) , решений нет

в) если b = 1, то –2х + 2 = 0; х = 1

если b  1; .

б) таких b не существует;

8. При каких значениях a уравнения и равносильны?

1) При : имеет два различных корня, имеет один корень. Равносильности нет.

2) При решения уравнений совпадают.

3) При ни первое, ни второе уравнения решений не имеют. Как известно, такие уравнения считаются равносильными.

Ответ: при .

9. График функции у=3х 2 — k х+2 проходит через точку (-2;6). Найдите значение параметра k .

1. (Базовая задача 1. Увеличение технической сложности и добавление дополнительных условий.)

При каких значениях параметра а уравнение является:

б) неполным квадратным;

а, б )

Уравнение является неполным квадратным, если:

если а  (–  ; – 2)  (– 2; 0)  (0; 1)  (1; +  ), то исходное уравнение является квадратным.

В ) Уравнение явл. Линейным, если при а = 0 или а = 1.

2. (Базовая задача 2. Увеличение трудности задачи)

При каких значениях параметра b уравнение

а) имеет корни; б) не имеет корней?

Решение: _, D = , D =

а) , но , следовательно, ;

если , то уравнение корни имеет.

Б) – при любых значениях b , кроме нуля;

если b  (–  ; 0)  (0; +  ), то исходное уравнение корней не имеет.

3. (Базовая задача 4. Увеличение громоздкости задачи)

При каких значениях параметра p сумма корней квадратного уравнения х 2 +( p 2 + 4 p -5)х – p =0 равна 0?

4. (Базовая задача 4. Увеличение громоздкости задачи)

При каких значениях k произведение корней квадратного уравнения x 2 + 3 x + ( k 2 – 7 k + 12) = 0 равно нулю?

5. (Базовая задача 5. Возрастание трудности задачи)

Решите относительно х уравнение

Решение:

1) Если m = 0, то _, _.

2) Если m  0, то D = 36 – 4 m

, _;

б) 36 – 4 m = 0, m = 9, х = _;

в) 36 – 4 m m > 9, исходное уравнение корней не имеет.

Ответ: если m  (–  ; 0)  (0; – 9), то

если m  (9; +  ), то корней нет.

6. (Базовая задача 9. Необычная форма предоставления условия задачи, при которой сразу не видно применение знакомого способа действий)

Найдите, при каком значении параметра q абсцисса вершины параболы у=(х-5 q ) 2 — q 2 + q +12 отрицательна, а ордината – положительна.

7. (Базовая задача 4. Необычная форма предоставления условия задачи, увеличение громоздкости)

Корни уравнения таковы, что . Найдите а .

Решение.
По теореме Виета и . Возведём обе части первого равенства в квадрат: . Учитывая, что , а , получаем: или , , . Проверка показывает, что все значения удовлетворяют условию.
Ответ:

8. (Базовая задача 7. Увеличение технической сложности задачи, варьирование известного алгоритма)

Решите уравнение , если известно, что один из корней вдвое больше другого.

Запишем формулы Виета: и учтем, что . Подставим эту связь между корнями в формулы Виета и получим или

Из первого уравнения находим: и подставляем во второе:

После этого определяем и

9. (Базовая задача 5. Увеличение трудности задачи)

При каких а уравнение имеет более одного корня?

При а = 0 уравнение имеет единственный корень, что не удовлетворяет условию.

При а  0 исходное уравнение, будучи квадратным, имеет два корня, если его дискриминант – положительный. Отсюда получаем: . Однако в полученный промежуток (– 4; 1) входит число 0, которое, как мы уже проверили, неприемлемо.

Ответ: или .

10. (Базовая задача 5. Аналог предыдущей задачи 9, увеличение трудности и громоздкости)

При каких а уравнение имеет более одного корня?

Стандартный шаг – начать со случаев а = 0 и а = – 3.

При а = 0 уравнение имеет единственное решение. При а = – 3 решением уравнения является любое действительное число.

При а  0 и а  – 3, разделив обе части данного уравнения на а + 3, получим квадратное уравнение , дискриминант которого положителен при а > – .

Из промежутка ( –; +  ) надо исключить точку а = 0, а в ответ не забыть включить а = – 3.

Ответ: а = – 3, или – 0.

11. (Базовая задача 8. Увеличение трудности и громоздкости)

При каких значениях b уравнения и равносильны?

12. (Базовая задача 5. Варьирование известного алгоритма решения задачи)

Найдите значения а, при которых оба корня уравнения не превосходят 1.

По условию задачи корни , т.е. или откуда
Ответ: при .

13. (Базовая задача 5. Варьирование известного алгоритма решения задачи)

При каких значениях корни уравнения равны по модулю, но противоположны по знаку.

1. При каких значениях а оба корня уравнения х 2 – ах +2 = 0 лежат на интервале (0;3)?

Ответ: .

2. При каких значениях а один корень уравнения ах 2 +х +1 = 0 больше 2, а другой меньше 2?

3. Найдите все значения а, при которых уравнение 4х 2 – 2х + а = 0 имеет два корня, каждый из которых принадлежит интервалу (-1;1).

4. При каких значениях корни уравнения равны по модулю, но противоположны по знаку?

5. Решите уравнение .

Данное уравнение можно переписать в виде

Рассматривая его как уравнение относительно переменной и параметром , найдем дискриминант:

Так как необходимым и достаточным условием существования решения квадратного уравнения является неотрицательность его дискриминанта, получим, что это возможно лишь, если .

Подставляя в уравнение найденное значение, получим, что

Таким образом, нам действительно удалось решить данное уравнение, хотя это уравнение с двумя переменными.

Замечание: При решении данной задачи был использован еще один основополагающий принцип решения задач с параметрами – параметром может быть объявлена любая переменная, входящая в уравнение.

Ответ: .

Данный принцип хорошо иллюстрируется следующими двумя примерами, которые повторяют и расширяют материал.

6. Решите уравнение

Непосредственное решение этого уравнения как уравнения относительно переменной с параметром невозможно, т.к. это уравнение четвертой степени.

Рассмотрим данное уравнение как квадратное относительно переменной и параметром . Получим, что . Условием существования решения, т.е. выражения значения как функции , служит неотрицательность дискриминанта.

Таким образом, уравнение равносильно совокупности

Ответ:; ; , и

при любом значении .

В качестве параметра может выступать на каком-то этапе решения единственная переменная, входящая в уравнение.

7. Решите уравнение .

Представим это уравнение как квадратное относительно .

Данное решение подтверждает принцип свободы выбора неизвестной и параметра.

Таким образом, уравнение равносильно совокупности

Ответ: ; ; ; .

Психологическая наука давно пришла к выводу, что лучше всего формировать и развивать мышление в ходе решения задач. В обучении математике они являются и целью, и средством обучения и математического развития школьников. В частности, это относится и к задачам с параметрами.

Добавление параметра значительно усложняет задачу, т.к. увеличивается ее размерность, появляется «глубина». Решение такой задачи требует системного подхода, целостного представления ситуации. Для решения уравнений (неравенств) с параметрами необходимо умение проводить разветвленные логические построения. При этом необходимо четко и последовательно следить за сохранением равносильности решаемых уравнений (неравенств), учитывая области определения выражений в них входящих.

Использование стандартных методов при решении задач с параметрами иногда приводит к необходимости выполнения очень громоздких вычислений, что существенно затрудняет решение. Такая ситуация, как правило, способствует началу творческих поисков других путей решений, их исследования, направленное на нахождение наиболее рационального, наиболее «красивого» способа решения. Под исследованием в науке понимается изучение какого-либо объекта с целью выявления закономерностей его возникновения, развития, преобразования. В процессе исследования синтезируются имеющиеся знания, накопленный опыт, а также методы и способы изучения объектов.

Из вышесказанного можно сделать вывод, что решение задач с параметрами развивает системное, логическое мышление. Являясь прекрасным материалом для исследовательской работы, решение уравнений (неравенств) с параметрами развивает такие умения как наблюдение, сравнение, обобщение и др.; учит творчески мыслить, способствует развитию гибкости мыслительного процесса и, что очень важно, развивает теоретическое мышление.

В. Локоть. Задачи с параметрами: иррациональные уравнения, неравенства, системы, задачи с модулем. — М.: АРКТИ, 2004.—64 с. (Абитуриент: Готовимся к ЕГЭ).

П. И. Горнштейн, В. Б. Полонский, М. С. Якир. Задачи с параметрами. 2007 год

3. Мордкович, А.Г. Алгебра. 8 кл [Текст] : Учебник для кл. с углубл. изуч. математики / А.Г. Мордкович.- М.: Мнемозина, 2007.

4. Мордкович, А.Г. Алгебра. 8 кл [Текст] : Задачник / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская.- М.: Мнемозина, 2007.

5. Научно – теоретический и методический журнал «Математика в школе» №4, 2004.

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

8.2.3. Теорема Виета

I. Теорема Виета для приведенного квадратного уравнения.

Сумма корней приведенного квадратного уравнения x 2 +px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Найти корни приведенного квадратного уравнения, используя теорему Виета.

Пример 1) x 2 -x-30=0. Это приведенное квадратное уравнение ( x 2 +px+q=0), второй коэффициент p=-1, а свободный член q=-30. Сначала убедимся, что данное уравнение имеет корни, и что корни (если они есть) будут выражаться целыми числами. Для этого достаточно, чтобы дискриминант был полным квадратом целого числа.

Находим дискриминант D=b 2 — 4ac=(-1) 2 -4∙1∙(-30)=1+120=121=11 2 .

Теперь по теореме Виета сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, т.е. (-p), а произведение равно свободному члену, т.е. (q). Тогда:

x₁+x₂=1; x₁∙x₂=-30. Нам надо подобрать такие два числа, чтобы их произведение было равно -30, а сумма – единице. Это числа -5 и 6. Ответ: -5; 6.

Пример 2) x 2 +6x+8=0. Имеем приведенное квадратное уравнение со вторым коэффициентом р=6 и свободным членом q=8. Убедимся, что есть целочисленные корни. Найдем дискриминант D₁, так как второй коэффициент – четное число. D₁=3 2 -1∙8=9-8=1=1 2 . Дискриминант D₁ является полным квадратом числа 1, значит, корни данного уравнения являются целыми числами. Подберем корни по теореме Виета: сумма корней равна –р=-6, а произведение корней равно q=8. Это числа -4 и -2.

На самом деле: -4-2=-6=-р; -4∙(-2)=8=q. Ответ: -4; -2.

Пример 3) x 2 +2x-4=0. В этом приведенном квадратном уравнении второй коэффициент р=2, а свободный член q=-4. Найдем дискриминант D₁, так как второй коэффициент – четное число. D₁=1 2 -1∙(-4)=1+4=5. Дискриминант не является полным квадратом числа, поэтому, делаем вывод: корни данного уравнения не являются целыми числами и найти их по теореме Виета нельзя. Значит, решим данное уравнение, как обычно, по формулам (в данном случае по формулам для частного случая с четным вторым коэффициентом). Получаем:

Пример 4). Составьте квадратное уравнение по его корням, если x₁=-7, x₂=4.

Решение. Искомое уравнение запишется в виде: x 2 +px+q=0, причем, на основании теоремы Виета –p=x₁+x₂=-7+4=-3 → p=3; q=x₁∙x₂=-7∙4=-28. Тогда уравнение примет вид: x 2 +3x-28=0.

Пример 5). Составьте квадратное уравнение по его корням, если:

II. Теорема Виета для полного квадратного уравнения ax 2 +bx+c=0.

Сумма корней равна минус b, деленному на а, произведение корней равно с, деленному на а:

Пример 6). Найти сумму корней квадратного уравнения 2x 2 -7x-11=0.

Решение.

Убеждаемся, что данное уравнение будет иметь корни. Для этого достаточно составить выражение для дискриминанта, и, не вычисляя его, просто убедиться, что дискриминант больше нуля. D=7 2 -4∙2∙(-11)>0. А теперь воспользуемся теоремой Виета для полных квадратных уравнений.

Пример 7). Найдите произведение корней квадратного уравнения 3x 2 +8x-21=0.

Решение.

Найдем дискриминант D₁, так как второй коэффициент (8) является четным числом. D₁=4 2 -3∙(-21)=16+63=79>0. Квадратное уравнение имеет 2 корня, по теореме Виета произведение корней x₁∙x₂=c:a=-21:3=-7.