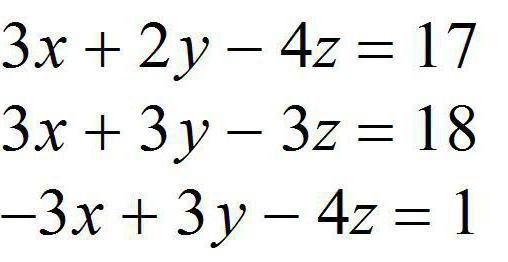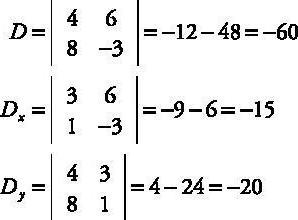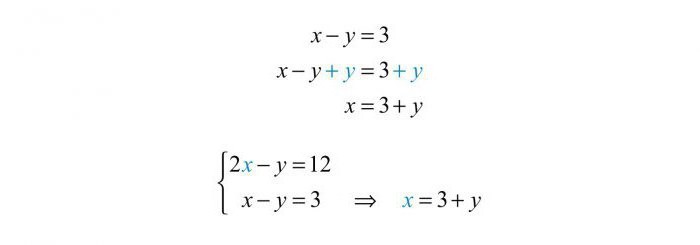Кто создал систему линейных уравнений

Ещё в школе каждый из нас изучал уравнения и, наверняка, системы уравнений. Но не многие знают, что существует несколько способов их решения. Сегодня мы подробно разберём все методы решения системы линейных алгебраических уравнений, которые состоят более чем из двух равенств.

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

История

На сегодняшний день известно, что искусство решать уравнения и их системы зародилось ещё в Древнем Вавилоне и Египте. Однако равенства в их привычном для нас виде появились после возникновения знака равенства «=», который был введён в 1556 году английским математиком Рекордом. Кстати, этот знак был выбран не просто так: он означает два параллельных равных отрезка. И правда, лучшего примера равенства не придумать.

Основоположником современных буквенных обозначений неизвестных и знаков степеней является французский математик Франсуа Виет. Однако его обозначения значительно отличались от сегодняшних. Например, квадрат неизвестного числа он обозначал буквой Q (лат.»quadratus»), а куб — буквой C (лат. «cubus»). Эти обозначения сейчас кажутся неудобными, но тогда это был наиболее понятный способ записать системы линейных алгебраических уравнений.

Однако недостатком в тогдашних методах решения было то, что математики рассматривали только положительные корни. Возможно, это связано с тем, что отрицательные значения не имели никакого практического применения. Так или иначе, но первыми считать отрицательные корни начали именно итальянские математики Никколо Тарталья, Джероламо Кардано и Рафаэль Бомбелли в 16 веке. А современный вид, основной метод решения квадратных уравнений (через дискриминант) был создан только в 17 веке благодаря работам Декарта и Ньютона.

В середине 18 века швейцарский математик Габриэль Крамер нашёл новый способ для того, чтобы сделать решение систем линейных уравнений проще. Этот способ был впоследствии назван его именем и по сей день мы пользуемся им. Но о методе Крамера поговорим чуть позднее, а пока обсудим линейные уравнения и методы их решения отдельно от системы.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Линейные уравнения

Линейные уравнения — самые простые равенства с переменной (переменными). Их относят к алгебраическим. Линейные уравнения записывают в общем виде так: а₁*x₁+а_2*x₂+. а_n*x_n=b. Представление их в этом виде нам понадобится при составлении систем и матриц далее.

Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Системы линейных алгебраических уравнений

Определение этого термина такое: это совокупность уравнений, которые имеют общие неизвестные величины и общее решение. Как правило, в школе все решали системы с двумя или даже тремя уравнениями. Но бывают системы с четырьмя и более составляющими. Давайте разберёмся сначала, как следует их записать так, чтобы в дальнейшем было удобно решать. Во-первых, системы линейных алгебраических уравнений будут выглядеть лучше, если все переменные будут записаны как x с соответствующим индексом: 1,2,3 и так далее. Во-вторых, следует привести все уравнения к каноническому виду: а₁*x₁+а_2*x₂+. а_n*x_n=b.

После всех этих действий мы можем начать рассказывать, как находить решение систем линейных уравнений. Очень сильно для этого нам пригодятся матрицы.

Видео:Система уравнений. Метод алгебраического сложенияСкачать

Матрицы

Матрица — это таблица, которая состоит из строк и столбцов, а на их пересечении находятся её элементы. Это могут быть либо конкретные значения, либо переменные. Чаще всего, чтобы обозначить элементы, под ними расставляют нижние индексы (например, а₁₁ или а₂₃). Первый индекс означает номер строки, а второй — столбца. Над матрицами, как и над любым другим математическим элементом можно совершать различные операции. Таким образом, можно:

1) Вычитать и складывать одинаковые по размеру таблицы.

2) Умножать матрицу на какое-либо число или вектор.

3) Транспонировать: превращать строчки матрицы в столбцы, а столбцы — в строчки.

4) Умножать матрицы, если число строк одной их них равно количеству столбцов другой.

Подробнее обсудим все эти приёмы, так как они пригодятся нам в дальнейшем. Вычитание и сложение матриц происходит очень просто. Так как мы берём матрицы одинакового размера, то каждый элемент одной таблицы соотносится с каждым элементом другой. Таким образом складываем (вычитаем) два этих элемента (важно, чтобы они стояли на одинаковых местах в своих матрицах). При умножении матрицы на число или вектор необходимо просто умножить каждый элемент матрицы на это число (или вектор). Транспонирование — очень интересный процесс. Очень интересно иногда видеть его в реальной жизни, например, при смене ориентации планшета или телефона. Значки на рабочем столе представляют собой матрицу, а при перемене положения она транспонируется и становится шире, но уменьшается в высоте.

Разберём ещё такой процесс, как умножение матриц. Хоть он нам и не пригодится, но знать его будет всё равно полезно. Умножить две матрицы можно только при условии, что число столбцов одной таблицы равно числу строк другой. Теперь возьмём элементы строчки одной матрицы и элементы соответствующего столбца другой. Перемножим их друг на друга и затем сложим (то есть, например, произведение элементов a₁₁ и а₁₂ на b₁₂ и b₂₂ будет равно: а₁₁*b₁₂ + а₁₂*b₂₂). Таким образом, получается один элемент таблицы, и аналогичным методом она заполняется далее.

Теперь можем приступить к рассмотрению того, как решается система линейных уравнений.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Метод Гаусса

Этой тему начинают проходить еще в школе. Мы хорошо знаем понятие «система двух линейных уравнений» и умеем их решать. Но что делать, если число уравнений больше двух? В этом нам поможет метод Гаусса.

Конечно, этим методом удобно пользоваться, если сделать из системы матрицу. Но можно и не преобразовывать её и решать в чистом виде.

Итак, как решается этим методом система линейных уравнений Гаусса? Кстати, хоть этот способ и назван его именем, но открыли его ещё в древности. Гаусс предлагает следующее: проводить операции с уравнениями, чтобы в конце концов привести всю совокупность к ступенчатому виду. То есть, нужно, чтобы сверху вниз (если правильно расставить) от первого уравнения к последнему убывало по одному неизвестному. Иными словами, нужно сделать так, чтобы у нас получилось, скажем, три уравнения: в первом — три неизвестных, во втором — два, в третьем — одно. Тогда из последнего уравнения мы находим первое неизвестное, подставляем его значение во второе или первое уравнение, и далее находим оставшиеся две переменные.

Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Метод Крамера

Для освоения этого метода жизненно необходимо владеть навыками сложения, вычитания матриц, а также нужно уметь находить определители. Поэтому, если вы плохо всё это делаете или совсем не умеете, придется поучиться и потренироваться.

В чём суть этого метода, и как сделать так, чтобы получилась система линейных уравнений Крамера? Всё очень просто. Мы должны построить матрицу из численных (практически всегда) коэффициентов системы линейных алгебраических уравнений. Для этого просто берём числа перед неизвестными и расставляем в таблицу в том порядке, как они записаны в системе. Если перед числом стоит знак «-«, то записываем отрицательный коэффициент. Итак, мы составили первую матрицу из коэффициентов при неизвестных, не включая числа после знаков равенства (естественно, что уравнение должно быть приведено к каноническому виду, когда справа находится только число, а слева — все неизвестные с коэффициентами). Затем нужно составить ещё несколько матриц — по одной для каждой переменной. Для этого заменяем в первой матрице по очереди каждый столбец с коэффициентами столбцом чисел после знака равенства. Таким образом получаем несколько матриц и далее находим их определители.

После того как мы нашли определители, дело за малым. У нас есть начальная матрица, и есть несколько полученных матриц, которые соответствуют разным переменным. Чтобы получить решения системы, мы делим определитель полученной таблицы на определитель начальной таблицы. Полученное число и есть значение одной из переменных. Аналогично находим все неизвестные.

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Другие методы

Существует ещё несколько методов для того, чтобы получить решение систем линейных уравнений. Например, так называемый метод Гаусса-Жордана, который применяется для нахождения решений системы квадратных уравнений и тоже связан с применением матриц. Существует также метод Якоби для решения системы линейных алгебраических уравнений. Он легче всех адаптируется для компьютера и применяется в вычислительной технике.

Видео:Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Сложные случаи

Сложность обычно возникает, если число уравнений меньше числа переменных. Тогда можно наверняка сказать, что, либо система несовместна (то есть не имеет корней), или количество её решений стремится к бесконечности. Если у нас второй случай — то нужно записать общее решение системы линейных уравнений. Оно будет содержать как минимум одну переменную.

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Заключение

Вот мы и подошли к концу. Подведём итоги: мы разобрали, что такое система и матрица, научились находить общее решение системы линейных уравнений. Помимо этого рассмотрели другие варианты. Выяснили, как решается система линейных уравнений: метод Гаусса и метод Крамера. Поговорили о сложных случаях и других способах нахождения решений.

На самом деле эта тема гораздо более обширна, и если вы хотите лучше в ней разобраться, то советуем почитать больше специализированной литературы.

Видео:Решение систем уравнений методом подстановкиСкачать

Презентация «Из истории решения систем уравнений».

Роль великих математиков в развитии методов решения систем уравнений.

Просмотр содержимого документа
«Презентация «Из истории решения систем уравнений».»

«Из истории решения систем уравнений»

Урок алгебры в 9 классе.

Автор: учитель первой категории Кочевых Р. П.

Кто хочет ограничиться

настоящим без знания прошлого,

тот никогда его не поймет.

В древневавилонских текстах, написанных в III – II тысячелетиях до н.э., содержится немало задач, решаемых с помощью составления систем уравнений, в которые входят и уравнения второй степени. Вот одна из них. Площади двух своих квадратов я сложил: . Сторона второго квадрата равна стороны первого и еще 5. Соответствующая система уравнений в современной записи имеет вид:

• Для решения этой системы вавилонский автор возводит во втором уравнении у в квадрат, получает ,
• Подставив это значение в первое уравнение, получает .
• Решая уравнение, находит х , затем у.
• Так как вавилоняне не имели обозначений для многих неизвестных, то они прилагали немало усилий для выбора неизвестного таким образом, чтобы свести решение системы к решению одного уравнения.

Математик эпохи эллинизма, один из основоположников алгебры. Жил и работал в Александрии.

Ввел буквенную символику. Работы Диофанта в области теории чисел послужили основанием для дальнейших исследований.

Его именем названы: диофантовы уравнения — алгебраические уравнения или системы алгебраических уравнений с рациональными коэффициентами, решения которых отыскиваются в целых и рациональных числах.

Диофант -последний из великих математиков античности.

Задача Найти два натуральных числа, зная, что их сумма равна 20, а сумма их квадратов 208. Мы бы решали эту задачу составлением системы уравнений:

Диофант же, выбирая в качестве неизвестного половину разности искомых чисел, получает ( в современных обозначениях):

x 2 + y 2 = (z + 10) 2 + (10 – z) 2 = 2z 2 + 200, а по условию это равно 208,

z = ± 2; z = — 2- не удовлетворяет условию задачи, поэтому, если z = 2, то

В XVII — XVIII в.в. приемы исключения при решении систем уравнений разрабатывали Ферма, Ньютон, Лейбниц, Эйлер, Безу, Лагранж В современной записи система двух линейных уравнений с двумя неизвестными имеет вид

• Решение этой системы выражается формулами

Нижние индексы при буквах впервые употребил в 1675 году немецкий математик Лейбниц, что в большей мере способствовало созданию теории определителей.

31.III. 1596 – 11.II. 1650

Родился в 1596 г. в городе Лаэ во Франции в дворянской семье. Отец хотел из сына сделать офицера. Но Рене интересовала математика. Вскоре он познакомился с Мерсеном, а затем и с другими математиками Франции.

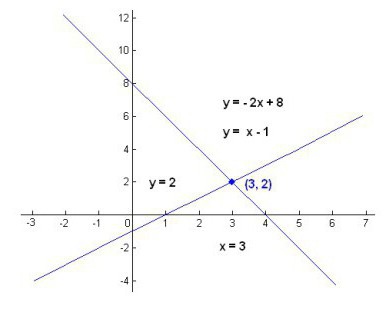
Будучи в армии, Декарт изучил алгебру немецких, математику французских и греческих ученых. Декарт был крупнейшим философом и математиком своего времени. Самым известным его трудом является «Геометрия». Декарт ввел прямоугольную систему координат, установил соответствие между числами и отрезками прямой и таким образом ввел алгебраический метод в геометрию. Это позволило решать системы уравнений графическим методом. Эти открытия Декарта дали огромный толчок развитию математики.

Крамер Габриель (1704-1752)- швейцарский математик. Учился и работал в Женеве. Основные труды по высшей алгебре и аналитической геометрии.

Установил и опубликовал (1750г.) правила решения систем n линейных уравнений с n неизвестными с буквенными коэффициентами (правило Крамера), заложил основы теории определителей .

– 23.02.1855) немецкий математик, внесший фундаментальный вклад также в астрономию и геодезию, почетный член Петербургской Академии Наук, именем которого назван метод решения

— развитие методов решения систем уравнений прошло длинный путь; — только благодаря трудам ученых решение систем уравнений приняло современный вид.

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Системы уравнений: история, понятия

Система уравнений — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.

Решением системы уравнений называется упорядоченный набор чисел — значений неизвестных, при подстановке которых каждое уравнение системы обращается в верное равенство.

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

$$left<begin a_ cdot x_+a_ cdot x_+ldots+a_ cdot x_=b_ \ a_ cdot x_+a_ cdot x_+ldots+a_ cdot x_=b_ \ ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots . . \ a_ cdot x_+a_ cdot x_+ldots+a_ cdot x_=b_ endright.$$

Упорядоченный набор значений $left<x_^, x_^, ldots, x_^right>$ называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.

Видео:6 способов в одном видеоСкачать

История систем уравнений

Задачи, соответствующие современным задачам на составление и решение систем уравнений с несколькими неизвестными, встречаются еще в вавилонских и египетских рукописях II века до н.э., а также в трудах древнегреческих, индийских и китайских мудрецов. В китайском трактате «Математика в девяти книгах» словесно изложены правила решения систем уравнений, были замечены некоторые закономерности при решении.

Видео:Как ЛЕГКО РЕШАТЬ Систему Линейный Уравнений — Метод СложенияСкачать

Основные понятия и применения

Система может состоять из алгебраических уравнений, линейных алгебраических уравнений, нелинейных уравнений, дифференциальных уравнений.

Методы решения системы уравнений зависят от типа системы. Например, решения систем линейных алгебраических уравнений хорошо известны ( метод Крамера, метод Гаусса, матричный метод, метод итераций и т.д.). Для нелинейных же систем общего аналитического решения не найдено, они решаются разного рода численными методами. Аналогично дело обстоит и с системами дифференциальных уравнений.

Системы линейных уравнений широко используются в задачах экономики, физики, химии и других науках.

Решение систем линейных алгебраических уравнений — одна из основных задач вычислительной линейной алгебры. Хотя задача решения именно системы линейных уравнений сравнительно редко представляет самостоятельный интерес для прикладных задач, но от умения эффективно решать данные системы часто зависит сама возможность математического моделирования самых разнообразных процессов с применением ЭВМ. Значительная часть численных методов решения различных (в особенности — нелинейных) задач включает в себя решение систем линейных уравнений как элементарный шаг соответствующего алгоритма.

🎥 Видео

Метод Гаусса решения систем линейных уравненийСкачать

Системы линейных уравнений. Пример 02.Скачать

Алгебра 7. Урок 8 - Системы линейных уравненийСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Видеоурок "Однородные системы линейных уравнений"Скачать

Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать