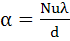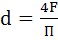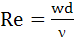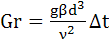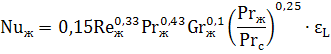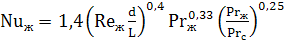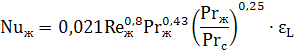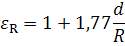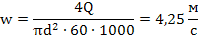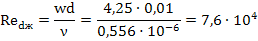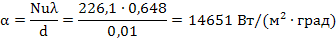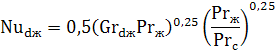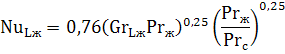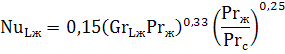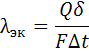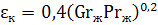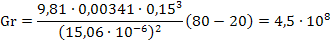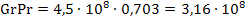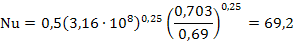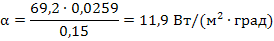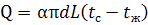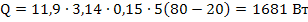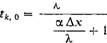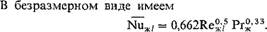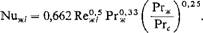Критериальное уравнение м а михеева

7.4.1.Теплоотдача в прямолинейных каналах

Интенсивность теплоотдачи в прямых гладких каналах при вынужденной конвекции определяется в основном режимом движения теплоносителя.

Ламинарный режим. При ламинарном движении необходимо учитывать влияние естественной конвекции. Наличие ее меняет закон распределения скорости в сечении, что сказывается на интенсивности теплообмена.

Для определения коэффициента теплоотдачи при ламинарном течении теплоносителя в прямых гладких трубах при (l/d)>50 используется критериальное уравнение М.А. Михеева [6]:

. (7.15)

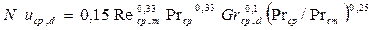
Здесь индекс „ср“ у критериев обозначает, что в качестве определяющей температуры принята средняя по длине канала температура теплоносителя. Критерий же Pr_cm определяется для теплоносителя при температуре стенки. Определяющим размером в этом уравнении является эквивалентный диаметр. Отношение Pr_cp/Pr_cm в уравнениях (7.14, 7.15) учитывает влияние на теплоотдачу направления теплового потока. Так как величина критерия Прандтля для жидкостей с увеличением температуры уменьшается, то при Т_cm>T_m отношение Pr_cp / Pr_cm будет больше единицы, в случае T_m> T_cm это отношение меньше единицы. Отсюда при прочих равных условиях теплоотдача интенсивнее в случае направления теплового потока от стенки к теплоносителю. Это явление можно объяснить меньшей толщиной теплового пограничного слоя вследствие влияния температуры на вязкость теплоносителя.

Турбулентный режим. При турбулентном режиме движения теплоноситель в канале весьма интенсивно перемешивается, и естественная конвекция не оказывает влияния на теплоотдачу. Для определения среднего коэффициента теплоотдачи при развитом турбулентном движении повсеместно используется критериальное уравнение М.А. Михеева [6].

(7.16)

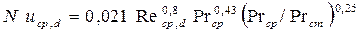
Для воздуха эта формула упрощается:

(7.17)

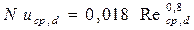
Индексы у критериев теплового подобия „ cp“ и „ d “ показывают, что за определяющую температуру принята средняя температура теплоносителя по длине канала, а определяющий размер ─ эквивалентный диаметр канала. Уравнения (7.16) и (7.17) применимы для прямых гладких труб при (l/d)>50 в пределах Re = 1×10 4 . 5×10 5 и Pr = 0,6 . 2500.

Для переходного режима (от ламинарного к турбулентному) надежных критериальных уравнений нет. Для определения приближенного коэффициента теплоотдачи в этой области можно использовать уравнение, рекомендованное в [6].

(7.18)

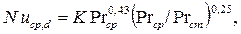
где К определяют из табл. 7.1.

Т а б л и ц а 7.1

Re
K	3,6	4,9	5,9	7,5	12,2
Re
K	16,5

7.4.2.Теплоотдача на начальном участке канала

При вынужденном движении теплоотдача по длине канала неодинакова. Непосредственно у входа в канал коэффициент теплоотдачи имеет максимальное значение, на последующих участках длины он резко убывает, асимптотически приближаясь к некоторому постоянному значению,

рис. 7.5а. Такая закономерность объясняется полем скоростей теплоносителя, (см. рис. 7.5 b).

На входе в канал скорость теплоносителя одинакова по всему его сечению, динамический пограничный слой только начинает обозначаться, отсюда максимальное значение теплоотдачи. Далее, по каналу, скорость по сечению изменяется, толщина пограничного слоя растет, а коэффициент теплоотдачи падает. На некотором расстоянии от входа в канал скоростное поле стабилизируется, δ_д принимает постоянное значение, постоянным становится и коэффициент теплоотдачи α .

Участок канала от входа до сечения стабилизации температурного поля теплоносителя называют участкомтепловой стабилизации.

Экспериментально установлено, что для горизонтальных каналов длина участка тепловой стабилизации l_cm ≈ 50d_экв. Для определения коэффициента теплоотдачи на участке стабилизации используются те же уравнения, но с введением поправочного коэффициента , т.е.

Величина поправочного коэффициента ε_l определена экспериментально в зависимости от длины начального участка канала и значения Re, (табл. 7.2).

Фактор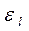
l/d
Re=2000	1,90	1,70	1,44	1,28	1,18	1,13	1,05	1,02	1,00
Re=20000	1,51	1,40	1,27	1,18	1,13	1,10	1,05	1,02	1,00
Re=200000	1,28	1,22	1,15	1,10	1,08	1,06	1,03	1,02	1,00

7.4.3. Теплоотдача в изогнутых каналах

При движении теплоносителя в изогнутых каналах (отводах, коленах, змеевиках) неизбежно возникает центробежный эффект, характер движения нарушается: поток теплоносителя отжимается к внешней стенке, отчего в поперечном сечении возникает так называемая в т о р и ч н а я ц и р к у-

л я ц и я, рис. 7.6.

Это приводит к значительному повышению коэффициента теплоотдачи по сравнению с его значением для прямых каналов. Теплоотдача в таких каналах рассчитывается по формулам для прямолинейных каналов с последующим умножением на поправочный коэффициент . Для змеевиковых труб значение ε_R определяется по эмпирической формуле:

, (7.19)

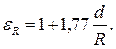
где d – диаметр трубы;

R – радиус кривизны канала.

7.4.4. Теплообмен потока с преградами

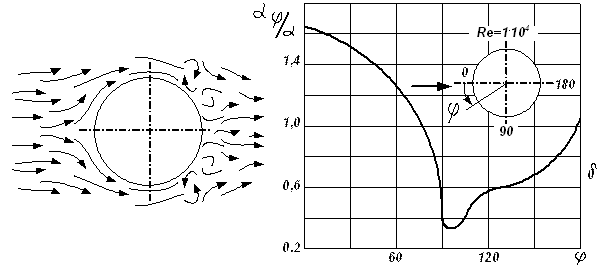
При обтекании тел, стоящих на пути движения теплоносителя, форма их поверхности определяет условия формирования пограничного слоя и поэтому существенно влияет на интенсивность теплоотдачи. На рис. 7.7 а показана картина течения при поперечном обтекании цилиндра (трубы). В месте натекания потока на поверхность образуется пограничный слой, толщина которого по мере движения теплоносителя вдоль образующей цилиндра увеличивается. Затем происходит отрыв потока, и образуются вихри.

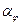
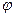
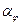
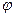
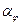
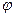
С изменением характера обтекания меняется и коэффициент теплоотдачи. На рис. 7.7 б показано изменение относительного значения коэффициента теплоотдачи по окружности цилиндра. Здесь — местное значение коэффициента теплоотдачи, α — среднее его значение по контуру. Как видно из рисунка, в месте набегания потока на цилиндр ( = 0) коэффициент максимален. С увеличением угла теплоотдача резко падает и при = 90 …100 о , т.е. в области отрыва потока от поверхности, имеет минимальное значение. При > 120 о интенсивность теплоотдачи возрастает вследствие вихреобразований.

Если теплоноситель натекает на цилиндр под прямым углом к его оси, то среднее значение коэффициента теплоотдачи можно вычислить с использованием критериального уравнения, [4].

, (7.20)

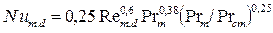
Которое справедливо в пределах 10 3 5 и 0,6 3 .

Другие критериальные уравнения, описывающие конвективный теплообмен при взаимодействии теплоносителя с преградами, приведены в Приложении табл. 13.

7.4.5. Теплоотдача в газоходах

Часто теплотехнические задачи состоят в необходимости определения коэффициентов теплоотдачи в каналах различных форм и размеров, например, газоходах котельных установок, в цилиндрах и теплообменниках поршневого компрессора, в коллекторах и глушителях ДВС и т.п. При этом теплоноситель может быть в виде а э р о з о л е й. Аэрозоль – это коллоидная система, состоящая из газовой среды, в которой взвешены твердые или жидкие частицы (дым, туман).

Теплоотдачу аэрозолей в прямых гладких каналах можно определить по критериальному уравнению, рекомендованному в работе [12],

, (7.21)

Nu_г,d – критерий Нуссельта чистого газа;

– объемная доля частиц в газе;

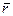
c_m и ρ_mр – массовая теплоемкость и плотность частиц, соответственно;

c_г и ρ_г – массовая теплоемкость и плотность газа, соответственно.

Для газоходов в виде коротких каналов при определении критерия Нуссельта чистого газа при Re> 10 4 можно использовать выражение:

(7.22)

Здесь Nu_m,d – среднее по длине канала значение Нуссельта. За определя -ющую температуру принята температура теплоносителя на входе в канал, за определяющий размер – d_экв. В криволинейных газоходах интенсивность теплоотдачи возрастает, найденное по уравнению (7.22) значение α нужно умножить на поправочный коэффициент ε_R (7.19). В сечениях газоходов, где теплоноситель меняет направление течения на угол 90 о и более, значение коэффициента теплоотдачи возрастает примерно в 1,8 раза.

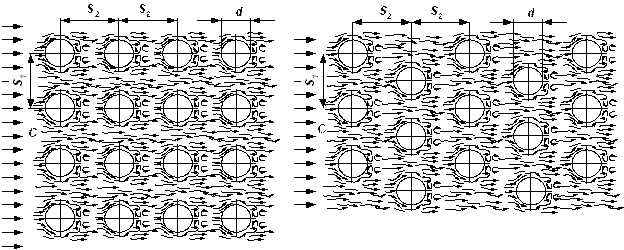
В некоторых типах газоходов теплоносителю приходится омывать трубчатые теплообменники. Такие теплообменники, как правило, выполняются в виде пучков труб с нормальным расположением к направлению движения теплоносителя. Различают коридорное и шахматное расположение труб в пучке, рис. 7.8.

Первый ряд труб в обоих пучках по условиям обтекания близок к одиночной трубе, трубы же последующих рядов находятся в других условиях. Если для шахматного пучка (см.рис.7.8 б) характер обмывания последующих рядов труб мало отличается от труб первого ряда, то для коридорного (см. рис. 7.8 а) эти отличия весьма существенны.

В коридорных пучках все трубы второго и последующих рядов находятся в вихревой зоне впереди стоящих труб, причем циркуляция теплоносителя в вихревой зоне слабая, так как поток в основном проходит в продольных зазорах между трубами . Поэтому в коридорных пучках как лобовая, так и кормовая части труб омываются со значительно меньшей интенсивностью, чем те же части одиночной трубы или труб первого ряда. В шахматных пучках характер обтекания глубоко расположенных труб качественно мало отличается от характера обтекания труб первого ряда.

Многочисленные исследования теплоотдачи пучков труб показали, что средняя теплоотдача первого и последующих рядов труб различна и определяется первоначальной турбулентностью потока. Начиная с третьего ряда, средняя теплоотдача стабилизируется. Если для третьего ряда теплоотдачу принять за 100 %, то для первого ряда шахматных и коридорных пучков она составит всего лишь 60 %, а для второго ряда — 70 % шахматного и 90 % коридорного пучков.

Теплоотдача пучков труб зависит также от расстояния между трубами, которое принято выражать в виде безразмерных характеристик s₁/d и s₂/d, называемых соответственноо т н о с и т е л ь н ы м п о п е р е ч н ы м

и п р о д о л ь н ы мш а г а м и.

Согласно [4], при режиме течения теплоносителя, соответствующем Re = 10 3 . 10 5 , средний коэффициент теплоотдачи, начиная с третьего ряда пучков труб, может быть найден по уравнению:

(7.23)

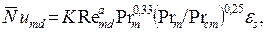
где для шахматных пучков К = 0,41, а = 0,6 и для коридорных – К = 0,26, а =0,65.

Поправочный коэффициент ε_s учитывает влияние относительных шагов. Для коридорного пучка ε_s = ( s₂ / d ) -0,15 ; для шахматного при s₁/s₂ 1/6 и при s₁/s₂ >2. ε_s = 1,2.

В формуле (7.23) определяющим размером является внешний диаметр труб d. Скорость теплоносителя подсчитывается по самому узкому поперечному сечению ряда пучка. За определяющую температуру принята температура теплоносителя перед соответствующим рядом пучка.

Для других режимов течения теплоносителя критериальные уравнения приведены в табл. 14 Приложения.

Критериальные уравнения теплообмена: расчет теплоотдачи в трубах и каналах

Теплоотдача при вынужденном течении жидкости в трубах и каналах

Теплоотдача в трубах и каналах может происходить при вынужденном или свободном характере конвекционных потоков (возможны также их сочетания в случае существенного влияния гравитационных сил).

При вынужденном течении (вынужденная конвекция) жидкость нагнетается или отводится под действием сил внешнего давления, например, ветра, насоса или вентилятора.

Свободное течение жидкости происходит под действием подъемных (гравитационных) сил за счет изменения ее плотности из-за разницы температуры – слой жидкости с меньшей плотностью стремиться занять верхнее положение относительно холодного слоя (свободная или естественная конвекция).

Интенсивность теплоотдачи, как при вынужденной, так и при свободной конвекции характеризуется коэффициентом теплоотдачи α, имеющим размерность Вт/(м 2 ·град), который определяется по формуле:

Nu – число Нуссельта; λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, равный

F – площадь сечения канала, м 2 ; П – периметр канала, м.

Для трубы круглого сечения, эквивалентный диаметр равен внутреннему диаметру трубы.

В целом, расчет коэффициента теплоотдачи сводится к определению числа Нуссельта, значение которого задается соответствующими критериальными уравнениями конвективного теплообмена, зависящими от режима течения жидкости и формы канала.

Течение жидкости в трубах определяется значением числа Рейнольдса Re и в зависимости от его величины может быть ламинарным, переходным или турбулентным.

• Ламинарный режим течения жидкости характеризуется величиной числа Re до 2300.
• При значении числа Re от 2300 до 10000 режим течения в трубах является переходным.
• Турбулентный режим течения в трубах наблюдается при числах Re более 10000.

Число (критерий) Рейнольдса представляет собой безразмерный комплекс, связывающий скоростные и вязкостные характеристики жидкости с определяющим размером канала (для трубы – это ее диаметр).

Число Re определяется по формуле:

w – скорость течения жидкости, м/с; d – эквивалентный диаметр канала, м; ν — кинематическая вязкость жидкости при средней температуре, м 2 /с.

Теплоотдача в трубах и каналах существенно зависит от режима течения жидкости. При ламинарном режиме интенсивность теплоотдачи значительно меньше, чем при развитом турбулентном.

Теплоотдача при ламинарном течении в трубах и каналах

Ламинарный режим течения жидкости обычно характеризуется низкой скоростью потока. При этом в некоторых случаях влиянием конвекции, обусловленной действием гравитационных сил, пренебрегать нельзя.

Для выбора правильного критериального уравнения теплообмена и оценки влияния естественной конвекции на интенсивность теплопередачи при ламинарном режиме служит критерий Грасгофа Gr.

g – ускорение свободного падения, м/с 2 ;

β – температурный коэффициент объемного расширения, град -1 ;

d – эквивалентный диаметр канала, м;

ν — кинематическая вязкость жидкости при средней температуре, м 2 /с;

Δt – средняя разность температур жидкости и стенки, °С.

Теплоотдача при ламинарном течении в трубах и каналах с учетом естественной конвекции. Если величина комплекса GrPr превышает 8·10 5 , то расчет коэффициента теплоотдачи необходимо проводить с учетом влияния естественной конвекции в потоке жидкости по следующему критериальному уравнению:

Индекс «ж» означает, что свойства среды, входящие в критерии подобия Re, Pr и Gr берутся при средней температуре жидкости.

Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки.

ε_L – коэффициент, учитывающий изменение теплоотдачи по длине трубы или канала. Его можно определить с помощью таблицы:

Значения коэффициента ε_L при ламинарном режиме

L/d	1	2	5	10	15	20	30	40	50
εL	1,9	1,7	1,44	1,28	1,18	1,13	1,05	1,02	1

Теплоотдача при ламинарном течении в трубах и каналах без учета естественной конвекции. При значении GrPr 5 , влияние естественной конвекции на теплоотдачу жидкости пренебрежительно мало, и расчет коэффициента теплоотдачи можно проводить по следующему критериальному уравнению:

d – эквивалентный диаметр канала, м;

L – длина трубы (канала), м.

Представленные критериальные уравнения теплообмена при ламинарном режиме позволяют определить среднее значение числа Нуссельта, по величине которого можно рассчитать средний коэффициент теплоотдачи:

λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, м.

Теплоотдача в трубах и каналах при турбулентном режиме

Теплоотдача в трубах и каналах при турбулентном режиме осуществляется путем передачи тепла при интенсивном перемешивании слоев жидкости. Критериальное уравнение теплообмена для расчета средней теплоотдачи в трубах и каналах в этом случае имеет вид:

Критерии подобия Re и Pr берутся при средней температуре жидкости. Число Прандтля с индексом «с» Pr_с берется при температуре стенки.

Представленное критериальное уравнение применяется в диапазоне чисел Re от 1·10 4 до 5·10 6 и Pr от 0,6 до 2500.

ε_L – коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы или канала при турбулентном режиме течения. Значения ε_L приведены в следующей таблице при различных числах Рейнольдса и отношениях длины канала к его эквивалентному диаметру:

Значения коэффициента ε_L при турбулентном режиме

Reж	L/d
	1	2	5	10	15	20	30	40	50
1·10 4	1,65	1,5	1,34	1,23	1,17	1,13	1,07	1,03	1
2·10 4	1,51	1,4	1,27	1,18	1,13	1,1	1,05	1,02	1
5·10 4	1,34	1,27	1,18	1,13	1,1	1,08	1,04	1,02	1
1·10 5	1,28	1,22	1,15	1,1	1,08	1,06	1,03	1,02	1
1·10 6	1,14	1,11	1,08	1,05	1,04	1,03	1,02	1,01	1

Расчет теплоотдачи в изогнутых трубах и каналах проводится по тому же критериальному уравнению с добавлением множителя — поправки на действие центробежных сил, которая определяется по формуле:

R — радиус изгиба трубы или канала, м; d – эквивалентный диаметр трубы или канала, м.

Теплоотдача в изогнутых трубах проходит более интенсивно, чем в прямых, за счет большего вихреобразования и лучшего перемешивания жидкости.

Расчет теплоотдачи при вынужденной конвекции

Пример расчета. Рассчитаем средний коэффициент теплоотдачи воды, текущей по трубопроводу длиной 1 м, диаметром d=0,01 м с расходом Q=20 л/мин. Средняя температура воды t_ж=50°С, температура стенки трубы t_с=10°С.

1. Определим физические свойства воды при температуре 50°С:

• Теплопроводность воды λ_ж= 0,648 Вт/(м·град);
• Плотность воды ρ_ж=988 кг/м 3 ;
• Кинематическая вязкость воды ν_ж=0,556·10 -6 , м 2 /с;
• Число Прандтля при температуре жидкости Pr_ж=3,54;
• Число Прандтля при температуре стенки Pr_с=9,52.

2. Рассчитаем среднюю скорость течения воды w по трубе:

3. Определим число Рейнольдса Re:

4. Поскольку число Рейнольдса имеет значение больше 1·10 4 , то режим течения является турбулентным и расчет теплоотдачи необходимо проводить по следующему критериальному уравнению:

Определим коэффициент ε_L по соотношению L/d=1/0,01=100. Поскольку L/d>50, то коэффициент ε_L=1_.

Выполним расчет числа Нуссельта по приведенному критериальному уравнению:

5. Рассчитаем средний коэффициент теплоотдачи от воды к стенке трубы по формуле:

Таким образом, средний коэффициент теплоотдачи от воды к стенке трубы составляет 14,65 кВт/(м 2 ·град).

Теплоотдача при свободной конвекции в трубах и каналах

Теплообмен при свободном движении жидкости (или газа) происходит вследствие разности плотностей нагретых и холодных ее слоев. Интенсивность теплоотдачи жидкости в трубах и каналах при свободной конвекции существенно зависит от их положения в пространстве относительно силы тяжести.

Теплоотдача при свободной конвекции имеет различный характер в случаях свободного течения в неограниченном пространстве и теплообмена в ограниченном объеме (в узкой трубе или канале).

Свободная конвекция в неограниченном пространстве

Конвекция в неограниченном пространстве протекает, например при охлаждении трубопровода центрального отопления, расположенного на улице в безветренную погоду, вблизи от которого отсутствуют препятствия для движения воздушных потоков.

Горизонтальный канал или труба. Интенсивность теплоотдачи при свободной конвекции зависит от величины комплекса GrPr. При значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу от поверхности горизонтальных труб и каналов, имеет вид:

В качестве определяющего размера принимается наружный диаметр d канала или трубы.

Вертикальный канал (труба, пластина). Для вертикальных труб и каналов при значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу, имеет вид:

При GrPr>10 9 :

Примечание: В приведенных критериальных уравнениях теплообмена свойства жидкости, входящие в числа Gr и Pr, определяются при температуре окружающей среды. Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки. В качестве определяющего размера принимается длина L (высота) вертикально стоящей трубы или канала.

Свободная конвекция в ограниченном объеме

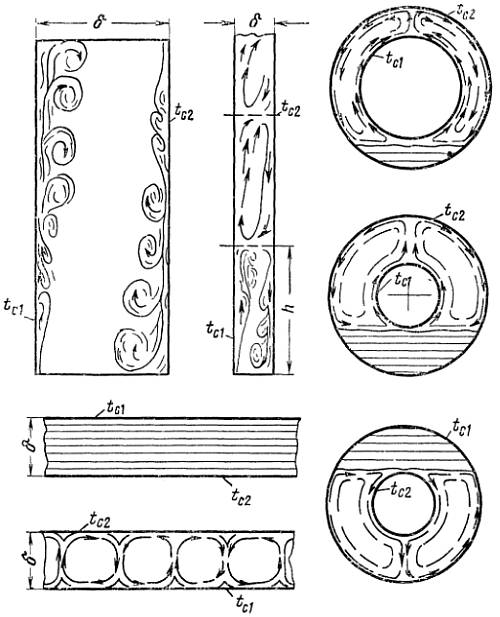
Теплообмен жидкости в ограниченном объеме при свободной конвекции характеризуется совместным протеканием процессов нагрева и охлаждения соседних слоев жидкости (или газа). Эти процессы сопровождаются сложным течением нисходящих и восходящих потоков, зависящих от рода жидкости, разницы температуры, формы канала и его геометрических размеров.

Для упрощения расчета таких сложных процессов конвективного теплообмена принято рассматривать их, как явление теплопроводности в щели толщиной δ с учетом понятия эквивалентного коэффициента теплопроводности λ_эк.

Эквивалентный коэффициент теплопроводности определяется по формуле:

Q — количество переданного тепла, Вт; δ — толщина слоя жидкости (или газа), м; F — площадь теплоотдающей поверхности, м 2 ; Δt=t_c1-t_c2 — температурный напор между нагретой и холодной стенками, °С.

Отношение эквивалентного коэффициента теплопроводности λ_эк к величине теплопроводности окружающей жидкости при средней температуре называется коэффициентом конвекции ε_к, который определяется значением комплекса GrPr.

При малых значениях комплекса GrPr 3 6 :

При 10 6 10 :

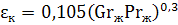
Примечание: Числа подобия Gr и Pr рассчитываются при средней температуре жидкости (или газа), равной t_ж=0,5(t_c1+t_c2). В качестве определяющего размера принимается δ — толщина слоя жидкости.

Расчет теплоотдачи при свободной конвекции

Пример расчета. Рассчитаем потери тепла естественной конвекцией от горизонтального трубопровода центрального отопления, находящегося на открытом воздухе. Диаметр трубопровода d=0,15 м, длина L=5 м, средняя температура наружной стенки t_с=80°С. Температура окружающего воздуха t_ж=20°С.

1. Определим физические свойства воздуха при температуре 20°С:

• Теплопроводность воздуха λ_ж= 0,0259 Вт/(м·град);
• Кинематическая вязкость воздуха ν_ж=15,06·10 -6 , м 2 /с;
• Число Прандтля при температуре жидкости Pr_ж=0,703;
• Число Прандтля при температуре стенки Pr_с=0,69;
• Коэффициент объемного расширения β_ж=1/(273+20)=0,00341 град -1 .

2. Вычислим число Грасгофа Gr по формуле:

3. Определим значение комплекса GrPr:

Этому значению комплекса соответствует следующее критериальное уравнение теплообмена при свободной конвекции в случае горизонтальной трубы:

4. Вычислим значение числа Нуссельта Nu:

5. Рассчитаем коэффициент теплоотдачи от трубы α по формуле:

6. Определим потери тепла с боковой поверхности трубопровода по формуле:

Подставляя численные значения, окончательно получаем потерю тепла:

Таким образом, только путем естественной (свободной) конвекции рассмотренный трубопровод отопления отдает воздуху 1681 Вт тепла.

КОНВЕКТИВНЫЙ ТЕПЛООБМЕН

Теплообмен между движущейся средой и поверхностью твердого тела называется конвективным теплообменом или теплоотдачей. Кон­вективный теплообмен обусловлен совместным действием конвектив­ного и молекулярного переноса теплоты (теплопроводности). Под кон­вективным переносом теплоты в среде с неоднородным распределением температуры понимают перенос, осуществляемый макроскопическими элементами среды при их перемещении, движении.

Различают движение вынужденное и свободное. Под вынужденным движением или вынужденной конвекцией жидкости понимают движение, вызванное действием внешних сил, приложенных на границах системы, поля массовых сил, приложенных к жидкости внутри системы, или за счет кинетической энергии, сообщенной жидкости вне системы.

Свободное движение или свободная (естественная) конвекция жид­кости — движение под действием неоднородного поля массовых сил, приложенных к частицам жидкости внутри системы и обусловленных внешними полями (например, гравитационным).

Различают ламинарный и турбулентный режимы течения. При лами­нарном режиме характер течения спокойный, слоистый, без переме­шивания (от лат. lamina — полоска, слой). Ламинарное движение жид­кости — это движение, при котором возможно существование стационар­ных траекторий ее частиц, часто повторяющих профиль канала.

При турбулентном движении течение жидкости неупорядоченное, вихревое (от лат. turbulentus — бурный, беспорядочный), с хаотично
изменяющимися во времени траекториями частиц, при котором в потоке возникают нерегулярные пульсации скорости и давления.

Переход ламинарного режима течения в турбулентный определя­ется значением числа Рейнольдса, которое называется критическим ReKp = vvKp//v. Чем больше Re, тем больше силы инерции по сравне­нию с силами вязкости, тем больше турбулентность потока.

Режим движения жидкости, промежуточный между ламинарным и турбулентным, называется переходным.

Течение жидкости состоит из основного потока и пограничного слоя. На твердой поверхности вследствие действия сил вязкого трения образуется тонкий слой заторможенной жидкости. Частицы жидкости, непосредственно прилегающие к поверхности теплообмена, как бы при­липают к ней. С возрастанием сил вязкости и, следовательно, с умень­шением числа Re происходит утолщение пограничного слоя. Чем больше Re, тем тоньше пристеночная область течения, тем тоньше пограничный слой.

Несмотря на то что пограничный слой остается тонким (а измере­ние скоростей показывает, что толщина его порой составляет несколько молекулярных слоев жидкости), он играет большую роль в процессах конвективного теплообмена.

Различают динамический и тепловой пограничные слои. Динами­ческим пограничным слоем называют пограничный слой жидкости, характеризующийся большим градиентом продольной составляющей скорости.

Тепловой пограничный слой характеризуется большим градиентом температуры, под действием которого осуществляется поперечный пере­нос теплоты. В области, непосредственно прилегающей к поверхности теплообмена, температура изменяется от гж — температуры основного потока до температуры стенки Tc. За пределами теплового пограничного слоя температура однородна и там явление переноса теплоты отсут­ствует. Тепловой пограничный слой по толщине 8Х может совпадать или не совпадать с динамическим 8 (рис. 2.28, 2.29). Соотношения толщин теплового и динамического пограничных слоев определяются значением числа Pr = V/A.

Как было показано выше, расчет теплоотдачи, несмотря на боль­шую сложность процесса, проводится по формуле Ньютона — Рихмана

Рис. 2.28. Схема дина­мического погранич­ного слоя

Рис. 2.29. Схема теплово­го пограничного слоя

Достаточно простого вида

Вся сложность расчета состоит в определении коэффициента тепло­отдачи. Согласно (2.229), коэффициент теплоотдачи определяется как плотность теплового потока при температурном напоре, равном одному градусу. Перенос теплоты в вязком пограничном слое осуще в — ляется путем теплопроводности и в соответствии с законом Фурье определяется соотношением

Сравнивая (2.229) и (2.230), получим коэффициент теплоотдачи

В первом приближении можно принять градиент температуры в теп­ловом пограничном слое равным

В этом случае коэффициент теплоотдачи будет определяться соот­ношением

Величина а зависит от всех факторов, влияющих на сам процесс теплообмена. К ним относятся скорость движения жидкости, физические свойства теплоносителя, характеристики температурного поля и гидро­динамические характеристики потока, геометрическая форма Ф и раз­меры / поверхности теплообмена:

Ос =/( 3-Ю6 вдоль пластины устанавливается устойчивый турбулентный режим течения. При значе­ниях 8 • 104 8Т и в направлении оси Z равен 1.

На основании закона сохранения энергии при стационарном тепло­вом режиме алгебраическая сумма тепловых потоков, проходящих через все плоскости, ограничивающие выделенный объем Dx — H— 1, равна нулю:

Где т2.З — масса жидкости, входящей через поверхность 2-3.

Величина т2.3 может быть определена по разности расходов ти2

Поток массы через плоскость 1-2

При прохождении расстояния dx поток массы изменится на вели­

Тогда поток через поверхность 3-4 будет

Поток массы через плоскость 2-3 будет

Поток теплоты через поверхность 2-3 выразится соответственно уравнением f

62-3 = P^Wo Dyj dx. (д)

Подставив в уравнение теплового баланса (а) выражения (в), (г), (д), получим

PCpVi^f dy J dx + Qc dx ■ 1 = 0.

После подстановки qc и некоторых преобразований получим оконча­тельное выражение интегрального уравнения энергии для пограничного слоя:

В уравнении (2.241) верхний предел интегрирования заменен на 5Х, так как при H > 5Т температура потока постоянна и равна температуре невозмущенного потока f0. В этом случае стоящая под знаком интеграла разность температур обращается в нуль. Выражение (2.241) впервые получено Г. И. Кружшшным. Для динамического пограничного слоя решение задачи было получено Т. Карманом (1921). В случае пластины интегральное уравнение динамического слоя имеет аналогичное выра­жение :

— j wx (vv0 — W) dy = V-—. (2.242)

Теплоотдача при ламинарном пограничном слое. Решением уравнений (2.241) и (2.242) можно определить толщину теп­лового пограничного слоя 5Т и коэффициент теплоотдачи согласно (2.233). Для этого необходимо знать распределение скорости wx (у) и температу­ры Ty по толщине теплового пограничного слоя.

Из опыта известно, что распределение в ламинарном потоке имеет параболический характер и может быть удовлетворительно описано уравнением кубической параболы, в которое в качестве неизвестного входит толщина пограничного слоя 6:

Уравнение квадратичной параболы неприемлемо, так как не удовлет­воряется условие на поверхности: при у = 0 и>Л. = 0 и >у = 0, так как в непосредственной близости от стенки инерционные силы равны нулю в связи с практически полным торможением потока (условие прилипания). В таком случае из уравнения движения для пограничного слоя (2.239) следует, что этого могло бы не быть, если бы в уравнение параболы входил член (у/5)2. В результате решения уравнения (2.243) совместно с граничными условиями (2.244) получим

Решим вторую часть задачи. Найдем распределение температуры T (у) по толщине теплового пограничного слоя.

Введем новую переменную — избыточную температуру 9 = T — Te и

= T0 — T„ считая температуру стенки Tc постоянной, не зависящей от х. В новом обозначении граничные условия запишутся:

В новых обозначениях форма интегрального уравнения энергии (2.241) не изменится

Для отыскания распределения температуры по толщине теплового пограничного слоя воспользуемся тем же методом, что и при опреде­лении распределения скорости. Вследствие подобия полей скорости и температуры примем параболическое распределение температуры

Вследствие идентичности граничных условий для скорости и избыточ­ной температуры (2.244) и (2.246) получим

З 90 , 1 S0 «=2ЇиЬ-ІГ

Окончательное распределение температуры в тепловом пограничном слое выражается уравнением

Из (2.248) и (2.242) и учитывая, что при у > 5 скорость равна постоян­ной величине w0 основного потока, а подынтегральное выражение ста­новится равным нулю, получаем выражение для определения толщины пограничного слоя

Решая последнее, получаем зависимость для толщины слоя

Или в безразмерном виде

Теперь, подставив полученные выражения скорости (2.245) и темпе­ратуры (2.248) в (2.241), вычислим интеграл в уравнении теплового потока в пределах теплового пограничного слоя, приняв 8Т ^ 8:

A v _ _ і 5 JL Оо ‘ 8Т

Считая 8T/8 ^ 1, вторым слагаемым можно пренебречь и считать

Правую часть уравнения (2.247) найдем из (2.248)

Подставив значение интеграла (2.252) и (2.253) в интегральное урав­нение теплового пограничного слоя (2.241), получим

W* (So — 3) dy = — 90w08 f ^

Или — vv0h3 8 — +2p282 ^

Подставляя в это уравнение значение толщины пограничного слоя согласно (2.249) и (2.250), получим

Решением этого уравнения будет

Показанное ранее соотношение толщин теплового и динамического пограничных слоев получило количественное выражение от Рг. Под­ставляя значение (2.251) в (2.255), получим окончательное выражение для 8Т:

8, = 4,64 _____ *__ .-. (2.256)

Определим коэффициент теплоотдачи

АЛ. Э0 = — X — и а, = — г — —. .

Величина градиента температуры на поверхности пластины легко определяется из уравнения (2.253):

Ду)у = о 2 8 , ‘ откуда получаем

Подставив 5Т согласно (2.256), получим окончательное уравнение для местного коэффициента теплоотдачи

Где С объединяет величины, не зависящие ОТ X.

Уравнение (2.258) легко привести к безразмерному виду, зная, что Nu* = OlXX/X:

Nu, = 0,331Re°-5Pr°-33. (2.260)

Среднее значение а для пластины длиной / определяется путем формального осреднения местного значения: І і

Где а і — местный коэффициент теплоотдачи на конце пластины длиной /.

Согласно (2.261) среднее значение а будет

А = 0,662 у >/Re, f/Pr.

В формуле (2.263) за определяющую температуру принята средняя температура жидкости, а за определяющий размер — длина пластины вдоль потока. Анализ полученной зависимости для а позволяет выявить роль основных факторов, влияющих на теплообмен.

Как видно из формулы (2.259), коэффициент теплоотдачи уменьшается с увеличением х. Это объясняется тем, что температурный напор £0 — Tc При постоянной температуре поверхности плиты не меняет своего значения, а при увеличивающейся толщине 5х(х) пограничного слоя градиент температуры падает с увеличением х.

Коэффициент теплоотдачи зависит и от направления теплового потока, зависит от того, нагревается жидкость или охлаждается. Градиент температуры в пограничном слое при нагревании больше, чем при охлаждении. Как показывает опыт и анализ влияния градиента температуры в случае нагревания и в случае охлаждения жидкости вдоль пластины, коэффициент теплоотдачи при нагревании капельных жид­костей больше, чем при охлаждении.

По предложению М. А. Михеева, зависимость коэффициента тепло­отдачи от направления теплового потока учитывается введением в кри­териальное уравнение множителя (Ргж/Ргс)0’25, где Prf относится к жидкости при температуре стенки. При нагревании жидкости эта поправка больше единицы, при охлаждении — меньше единицы.

Окончательное расчетное уравнение теплоотдачи при течении жидкости вдоль плоской поверхности:

Для газов Рг мало зависит от температуры, поэтому формула (2.264) может быть упрощена. Так, для воздуха, приняв Рг = 0,72, получим расчетное уравнение

Следует отметить, что наличие необогреваемого участка в начале плиты влияет на формирование динамического и теплового пограничных слоев. Это следует учитывать особой поправкой, которая может быть найдена в справочной литературе.

Приведенные зависимости, полученные на основе аналитического решения задачи теплообмена при ламинарном пограничном слое, совпадают с экспериментальными результатами обобщенных данных при постоянных физических свойствах жидкости (рис. 2.33). Такое совпадение свидетельствует о широких возможностях теории погранич­ного слоя при решении задач конвективного теплообмена. В этом разделе показан путь решения и анализ полученных результатов одной из
простых задач теплообмена. Для более сложных случаев мы огра­ничимся анализом результатов, полученных опытным путем.

Теплоотдача при турбулентном пограничном слое. Аналитический расчет теплоотдачи в турбулентном слое представляет большие трудности вследствие сложности самого движения и сложности механизма переноса количества движения и теплоты. Особенностью турбулентного течения является пульсационный характер движения. На рис. 2.34 показана осциллограмма колебаний скорости в фикси­рованной точке турбулентного потока. Отклонение мгновенной скорости w’ от средней w называется пульсацией. Наличие пульсаций как бы увеличивает вязкость, и тогда полная вязкость турбулентного потока будет суммой двух величин — молекулярной вязкости и дополнитель­ной турбулентной. Турбулентная вязкость рф не является физическим параметром теплоносителя, как коэффициент динамической вязкости, и характеризует интенсивность переноса количества движения в турбу­лентном потоке. Аналогично вязкости в уравнении движения, в дифферен­циальном уравнении энергии дополнительно к молекулярной тепло­проводности появляется турбулентная теплопроводность їгр, характе­ризующая турбулентный перенос теплоты и также не являющаяся физическим параметром теплоносителя.

Аналитическое решение дифференциальных уравнений становится невозможным вследствие трудностей, связанных с определением пульса- циоиных характеристик и их связи с осредненными параметрами потока.

Теоретическое исследование теплоотдачи при турбулентном движе­нии развивается на базе полуэмпирической теории турбулентности Прандтля или на базе гидродинамической теории теплообмена Рейнольдса, основанной на аналогии между процессами турбулентного переноса количества движения и теплоты. Рассмотрение этих вопросов не входит в задачи настоящего курса.

В заключение приведем расчетные формулы, полученные методом гидродинамической аналогии для расчета теплообмена в турбулент­ном потоке:

🎦 Видео