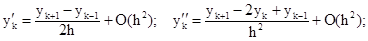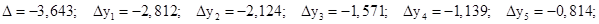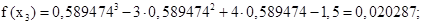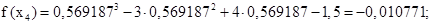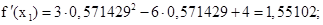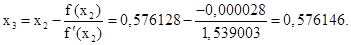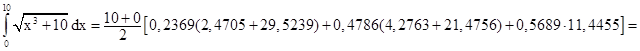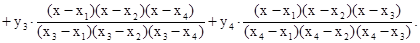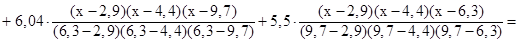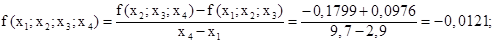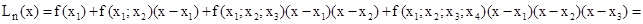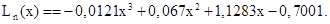Краевые задачи для обыкновенных дифференциальных уравнений примеры

Как было сказано в п. 10.1, в силу основной теоремы су­ществования и единственности решения для уравнения второ­го порядка

Определена задача Коши, когда в точке Х = X0 заданы значения неизвестной функции и ее производной:

Если выполнены условия теоремы 10.1, то задача Коши (10.13), (10.14) однозначно определяет частное решение.

Однако существует и другой тип задач для дифференци­альных уравнений второго порядка — значения неизвестной функции задаются в двух разных точках. Иными словами, при решении уравнения (10.13) на интервале (А, B) рассмотрим Гра­ничные условия наиболее простого вида на концах интервала

В этом случае уравнение (10.13) совместно с условиями (10.14) называется Первой краевой задачей для уравнения второго по­рядка. Поскольку второе условие в (10.15) равносильно второ­му условию в (10.14), то указанная краевая задача может иметь единственное решение, т. е. определять единственным образом частное решение дифференциального уравнения (10.13), прохо­дящее через точки (X1, Y1), (X2, Y2). Так, для линейного диффе­ренциального уравнения второго порядка первая краевая зада­ча имеет решение, если определитель системы линейных алгеб­раических уравнений относительно произвольных постоянных C1 и С2

Реализующей краевые условия (10.15), отличен от нуля. Здесь в соответствии с теоремой 10.4 (X) — частное решение не­однородного уравнения, У1(х) и У2(х) — линейно независимые решения соответствующего однородного уравнения. В таком случае краевая задача с условиями (10.15) однозначно опреде­ляет частное решение дифференциального уравнения (10.8).

Пример 1. Найти частное решение уравнения

Удовлетворяющее краевым условиям

Общее решение этого уравнения было найдено в примере 4 и. 10.3:

Для отыскания частного решения, соответствующего данным краевым условиям, подставим это решение в эти краевые усло­вия. Получаем систему линейных уравнений относительно про­извольных постоянных С1 и С2

Нетрудно видеть, что определитель этой системы не равен ну­лю, т. е. данная краевая задача имеет решение. Вычитая из второго уравнения первое, умноженное на 2, получаем С2, а затем из первого уравнения — С1:

Отсюда решение данной краевой задачи как частное решение дифференциального уравнения, проходящее через точки (0, 1) и (ln 2, 2), имеет вид

Видео:Краевые Задачи для Обыкновенных Дифференциальных УравненийСкачать

Конечно-разностный метод решения краевых задач.

для обыкновенных дифференциальных уравнений.

Примером краевой задачи является двухточечная краевая задача для обыкновенного дифференциального уравнения второго порядка:

с граничными условиями, заданными на концах отрезка [a; b]:

Следует найти такое решение у(х) на этом отрезке, которое принимает на концах отрезка значения у₀, у₁. Если функция линейна по аргументам , то задача поиска этой функции – линейная краевая задача, в противном случае – нелинейная..

Кроме граничных условий, задаваемых на концах отрезка и называемых граничными условиями первого рода, используются еще условия на производные от решения на концах — граничные условия второго рода:

или линейная комбинация решений и производных – граничные условия третьего рода:

где – такие числа, что

Возможно на разных концах отрезка использовать условия различных типов.

Наиболее распространены два приближенных метода решения краевой задачи:

— метод стрельбы (пристрелки);

Используя конечно-разностный метод, рассмотрим двухточечную краевую задачу для линейного дифференциального уравнения второго порядка на отрезке [а; b].

Введем разностную сетку на отрезке [а; b]:

Решение задачи будем искать в виде сеточной функции:

предполагая, что решение существует и единственно.

Введем разностную аппроксимацию производных следующим образом:

Подставляя эти аппроксимации производных в исходное уравнение, получим систему уравнений для нахождения y_k:

Приводя подобные члены и учитывая, что при задании граничных условий первого рода два неизвестных уже фактически определены, получим систему линейных алгебраических уравнений с трехдиагональной матрицей коэффициентов:

Для этой системы уравнений при достаточно малых шагах сетки h и q(x_k)

В первом случае линейная алгебраическая система аппроксимирует дифференциальную задачу в целом только с первым порядком (из-за аппроксимации в граничных точках), однако сохраняется трех диагональная структура матрицы коэффициентов. Во втором случае второй порядок аппроксимации сохраняется везде, но матрица линейной системы не трехдиагональная.

Пример. Решить краевую задачу:

с шагом 0,2.

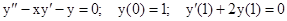
Во всех внутренних узлах отрезка [0; 1] после замены производных их разностными аналогами получим:

На левой границе y₀ = 1, на правой границе аппроксимируем производную односторонней разностью 1-го порядка:

С помощью группировки слагаемых, приведения подобных членов и подстановки значений x_k, а также с учётом у₀ = 1,получим систему линейных алгебраических уравнений:

.

В результате решения системы методом Крамера в Excel, получим:

Решением краевой задачи является табличная функция:

Расчетная часть

3.1. Найти действительные корни уравнения методами простых итераций и касательных (Ньютона) с точностью до 0,00001.

Решение: Для нахождения корня уравнения предварительно отделим корень уравнения графическим методом, записав уравнение в виде:

Построим в осях ХОУ графики функций:

:

Линии графиков пересекаются в единственной точке с абсциссой х₀, лежащей в интервале [0,5; 0,6], т.е.

Значение функции на концах интервала:

Т.к. знаки различны, то уравнение имеет единственный корень в интервале [0,5; 0,6].

3.1.1. Уточнение корня методом простых итераций.

Приведём исходное уравнение к виду:

Т.к. первая производная заданной функции в этом интервале положительна и численно первая производная на этом участке близка к 1,5, то константу С выбираем из интервала:

Т.о. итерационная функция приобретает вид:

Делаем первую итерацию:

Делаем вторую итерацию:

Делаем третью итерацию:

Делаем четвёртую итерацию:

Делаем пятую итерацию:

Делаем шестую итерацию:

Делаем седьмую итерацию:

Делаем восьмую итерацию:

Делаем девятую итерацию:

Продолжая далее, получаем:

На 19-ой итерации изменение шестого знака после запятой, позволяет утверждать, что пятый знак – после запятой – 5. Т.о. значение корня с заданной точностью:

3.1.2. Уточнение корня методом касательных (метод Ньютона):

Т.к. уравнение то же, то интервал, содержащий искомый корень, оставляем тот же [0,5; 0,6], т.е. а = 0,5; b = 0,6.

Находим первую и вторую производную функции :

Очевидно необходимые условия выполняются, т.к.:

, т.е. сохраняют знак на отрезке .

Выполняем первое приближение (х₀ = 0,5):

Выполняем второе приближение (х₁ = 0,571429):

Выполняем третье приближение (х₂ = 0,576128:

Выполняем четвёртое приближение (х₃ = 0,576146):

В пределах заданной точности f(x₂) оказался равен нулю, т.е. требуемая точность достигнута за 4 шага. Значение корня с заданной точностью:

3.2. Вычислить приближенное значение интеграла , используя формулы:

а) трапеций (n = 10); б) Симпсона (n = 10); в) Гаусса (n = 5).

Решение: Ограничимся в расчётах 4 знаками после запятой. Для приближённого вычисления определённого интеграла методом трапеций используется формула:

Разобьём интервал (–1; 9) на n = 10 отрезков (h =1) и вычислим значения подынтегрального выражения для начала и конца каждого отрезка.

№	0	1	2	3	4	5	6	7	8	9	10
х	0	1	2	3	4	5	6	7	8	9	10
	2,4495	2,6458	3,7417	5,7446	8,3666	11,4455	14,8997	18,6815	22,7596	27,1109	31,7175

Тогда по формуле трапеций, имеем:

Используя формулу Симпсона (формулу параболических трапеций) в виде:

получим:

Применяя к исходному интегралу квадратурную формулу Гаусса, имеем:

где

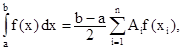
Для n = 5, коэффициенты t_i, представляющие нули полинома Лежандра и коэффициента А_i (эти значения табулированы в справочных таблицах) составляют:

i	1	2	3	4	5
ti	–0,9061	–0,5385	0	0,5385	0,9061
A1	0,2369	0,4786	0,5689	0,4786	0,2369
хi	0,4695	2,3075	5	7,6925	9,5305
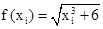	2,4705	4,2763	11,4455	21,4756	29,5239

3.3. Построить интерполяционные многочлены Лагранжа и Ньютона по следующим табличным данным:

	2,9	4,4	6,3	9,7
	2,84	4,53	6,04	5,50

Проверить совпадение значений интерполирующего многочлена с табличными значениями функции в узлах интерполяции.

Решение: Интерполяционный полином Лагранжа для четырёх узлов интерполяции записывается в виде:

Подставим численные значения из заданной таблицы:

Для составления интерполяционного полинома в форме Ньютона, вычислим разности первого порядка для заданной таблицы по формуле:

Вычислим разности второго порядка по формуле:

Вычислим разность третьего порядка по формуле:

Тогда интерполяционный полином Ньютона L_n(x) приобретает следующую форму:

Расчёты показывают, что оба интерполяционных полинома практически одинаковы, т.е. интерполяция ряда точек полиномом третьей степени осуществляется единственным образом.

По заданным узлам интерполяции х_i значения полинома по этому уравнению составляют:

Расчётные значения практически совпадают с заданными значениями f(x).

По полученному уравнению построена кривая, проходящая через узлы интерполяции.

3.4. Найти оценки параметров линейной и квадратичной моделей функциональной зависимости величин у и х по результатам наблюдений , приведенным в таблице:

	0,4	2,4	3,4	4,4	5,4
	2,14	2,14	2,24	2,34	2,34

Построить чертеж: на плоскости нанести экспериментальные точки , построить графики полученных эмпирических функций .

Решение: Коэффициенты «a₀ и а₁» линейной модели найдём, выполнив необходимые вычисления. Расчеты сведем в таблицу:

Номер наблюдения	1	2	3	4	5	Сумма
х	0,4	2,4	3,4	4,4	5,4	16
у	2,14	2,14	2,24	2,34	2,34	11,2
х 2	0,16	5,76	11,56	19,36	29,16	66
х∙y	0,856	5,136	7,616	10,296	12,636	36,54
	2,108	2,202	2,249	2,297	2,344	11,200
	0,0011	0,0039	0,0001	0,0019	0,0000	0,0069

Т.о. линейная зависимость у = а₀ + а₁х имеет вид: у = 2,08865 + 0,0473х.

По этой зависимости определены выровненные значения и остаточная сумма квадратов отклонений, которые записаны в нижних строках таблицы.

Коэффициенты а₀, а₁, а₂ квадратичной зависимости найдём, также выполнив необходимые расчёты в таблице:

Номер наблюдения	1	2	3	4	5	S
х	0,4	2,4	3,4	4,4	5,4	16
у	2,14	2,14	2,24	2,34	2,34	11,2
х 2	0,16	5,76	11,56	19,36	29,16	66
х 3	0,064	13,824	39,304	85,184	157,464	295,84
х 4	0,0256	33,1776	133,634	374,81	850,306	1391,95
у·х	0,856	5,136	7,616	10,296	12,636	36,54
у·х 2	0,3424	12,3264	25,8944	45,3024	68,2344	152,1
	2,128	2,182	2,230	2,292	2,368	11,200
	0,0001	0,0018	0,0001	0,0023	0,0008	0,0051

Составим систему уравнений:

Решение этой системы методом Крамера даёт:

Т.о. квадратичная зависимость у = а₀ + а₁х + а₂х 2 имеет вид:

у = 2,12433 + 0,00729·х + 0,006996·х 2 .

В нижней строке таблицы по полученному уравнению тоже рассчитаны значения по заданным значениям Х и остаточная сумма квадратов отклонений, которые записаны в нижних строках таблицы.

Эмпирическая ломаная, а также линии линейной и квадратичной модели построены на рисунке.

Результаты и выводы.

1. Т.о. интерполяционный полином Лагранжа и Ньютона, построенный по 4 заданным узлам интерполяции имеет вид:

Значения функции, вычисленные по этому полиному третьей степени, точно совпадают с заданными значениями в узлах интерполяции.

Полученное уравнение позволяет найти приближённые значения функции в любых промежуточных точках от х₁ = 2,9 до х₄ = 9,7.

2. Применение метода минимальных квадратов (МНК) к аппроксимации пяти экспериментальных точек линейной зависимостью вида у = а₀ + а₁х, т.е. прямой линией и квадратичной зависимостью вида 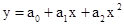, т.е. параболой дало следующие выражения:

– линейная зависимость реализована уравнением: у = 2,0887 + 0,0473х

– квадратичная зависимость реализована уравнением: у = 2,1243 + 0,0073·х + 0,007·х 2 .

Судя по остаточной сумме квадратов отклонений, квадратичная зависимость несколько лучше аппроксимирует экспериментальные данные, т.к. для неё остаточная сумма квадратов отклонений меньше, чем для линейной функции.

Список использованной литературы

1. Самарский А.А. Гулин А.В. Численные методы. М. МГУ. 1989 год.

2. Н. С. Бахвалов; Н.П. Жидков; Г.М. Кобельков. Численные методы. М 2003 год;

3. В.А. Буслов, С.Л.Яковлев. Численные методы и исследование функций. СПГУ. Курс лекций. СПБ 2001 г

4. Г.А. Зуева. Метод наименьших квадратов и его применение. Электронное учебное пособие. Иваново, 2009

Видео:Дифференциальные уравнения | задача Штурма - Лиувилля | классические краевые задачи | 1Скачать

«Краевая задача для дифференциального уравнения 2-го порядка. Примеры»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Ленинградский государственный университет имени А.С.Пушкина

Кафедра высшей математики

Курсовая работа по дифференциальным уравнениям на тему:

«Краевая задача для дифференциального уравнения 2-го порядка. Примеры»

студентки 3 курса,

физики и информатики

(ФИО, уч степень, уч звание, долж-ть)

Санкт-Петербург, 2010 г.

Цель курсовой работы исследовать дифференциальные уравнения второго порядка, в частности проанализировать решение краевых задач для дифференциального уравнения второго порядка.

В данной курсовой работе речь пойдет о дифференциальных уравнениях второго порядка и краевых задачах для данного типа уравнений. Мы рассмотрим следующие понятия:

Дифференциальные уравнения второго порядка;

Так же рассмотрим применение краевых задач в практической жизни человека, на примере уравнения колебаний струны.

Глава 1. Краевая задача для дифференциального уравнения второго порядка стр.5

§1. Общие сведения о дифференциальных уравнениях второго порядка стр.5

п.1.1. Общие понятия стр.5

п.1.2. Механический смысл дифференциального уравнения второго порядка

§2. Введение в краевые задачи стр.8

п.2.1.Определение краевой задачи стр.8

п.2.2.Постановка краевой задачи стр.8

§3. Линейная краевая задача. Сведение ее к задаче Коши стр.11

§4. Функция Грина стр.14

Глава 2. Применение краевых задач на практике стр.15

§1. Краевая задача для дифференциального уравнения второго порядка, в частных производных стр.15

п.1. Дифференциальные уравнения в частных производных стр.15

п.2. Вывод уравнения колебаний струны. Понятие о граничных и начальных условиях стр.17

§2. Решение обыкновенных дифференциальных уравнений второго порядка с заданными краевыми условиями стр.20

Список литературы стр.25

Дифференциальные уравнения – это уравнения, содержащие искомые функции, их производные различных порядков и независимые переменные. Теория дифференциальных уравнений возникла в конце 17 века, под влиянием потребностей механики и других естественнонаучных дисциплин, по существу одновременно с интегральным и дифференциальным исчислением.

Простейшие дифференциальные уравнения встречались уже в работах И.Ньютона и Г.Лейбница; термин «дифференциальные уравнения» принадлежит Лейбницу.

Под обыкновенным дифференциальным уравнением понимается равенство, содержащее независимую переменную, неизвестную функцию от этой переменной и ее производные. Порядком старшей производной, входящей в состав уравнения задается порядок дифференциального уравнения. Функцией, имеющей соответствующие производные и обращающие уравнение в тождество, определяется решение дифференциального уравнения. Процесс нахождения решений дифференциального уравнения называют его интегрированием.

В данной курсовой работе рассмотрим обыкновенные дифференциальные уравнения второго порядка, в частности краевые задачи для дифференциального уравнения второго порядка. А так же во второй главе познакомимся с дифференциальными уравнениями в частных производных, на примере уравнения колебания струны.

Для достижения цели, представленной в предисловии необходимо выполнить следующие задачи:

Ознакомиться с дифференциальными уравнениями второго порядка;

Ввести понятие краевой задачи;

Рассмотреть функцию Грина, и метод отыскания периодических решений;

Исследовать применение данных задач к практике.

Глава 1. Краевая задача для дифференциального уравнения второго порядка

В данной главе, мы познакомимся с обыкновенными дифференциальными уравнениями второго порядка, рассмотрим общие понятия о дифференциальных уравнения данного порядка (общие понятия и механический смысл). Также введем понятие краевой задачи и краевых условий для дифференциального уравнения второго порядка.

§1. Общие сведения о дифференциальных уравнениях второго порядка

п.1.1. Общие понятия

Дифференциальное уравнение второго порядка с неизвестной функцией у=у(х) имеет вид:

где F — данная функция.

Предполагая, что данное уравнение может быть однозначно разрешено относительно производной , получим:

, где f – некоторая функция.

Общее решение этого уравнения содержит две произвольные постоянные С ₁ и С ₂ . Поэтому через данную точку М ₀ (х ₀ ,у ₀ ), проходит пучок интегральных кривых, (рис.1) так как одна из произвольных постоянных остается неопределенной.

Чтобы выделить определенную интегральную кривую, кроме точки М ₀ , достаточно задать направление касательной в точке М ₀ к искомой интегральной кривой:

Таким образом, имеем следующие начальные условия:

Из начальных условий вытекает, что постоянные С ₁ и С ₂ должны удовлетворять системе уравнений:

.

Теорема о существовании и единственности решений:

Если в некоторой области где а, b , с – положительные числа, функция непрерывна и имеет ограниченные частные производные то существует единственное решение дифференциального уравнения , удовлетворяющее начальным условиям и определенное на некотором отрезке .

п.1.2. Механический смысл дифференциального уравнения второго порядка

Пусть по оси Ох движется материальная точка массы m (рис.2), причем действующая сила зависит от времени t , координаты точки x и ее скорости . На основании закона Ньютона имеем дифференциальное уравнение движения:

Следовательно, всякое дифференциальное уравнение второго порядка, разрешенное относительно старшей производной, можно рассматривать как дифференциальное уравнение прямолинейного движения материальной точки. Начальные условия принимают следующий вид:

,

т.е. в начальный момент t ₀ задаются: х ₀ – начальное положение точки и — ее начальная скорость.

§2. Введение в краевые задачи

п.2.1. Определение краевой задачи

Рассмотрим дифференциальное уравнение второго порядка, имеющее вид:

, (1)

Уравнение такого вида могут иметь бесконечное множество решений. Но на практике необходимо из множества решений выделять только одно. Для этого задают дополнительные условия на концах некоторого отрезка и получают задачу, которую называют краевой задачей.

Условия, которые задаются на концах отрезка называются краевыми условиями. Будем задавать линейные краевые условия вида:

Решением краевой задачи называется такое решение дифференциального уравнения, которое удовлетворяет заданным краевым условиям.

Однородная краевая задача всегда имеет решение: y ≡0 (тривиальное решение).

п.2.2. Постановка краевой задачи

Рассмотрим дифференциальное уравнение второго порядка: (3)

где у — искомая функция; х — независимая переменная; f — функция, определенная и непрерывная в некоторой замкнутой области D изменения своих аргументов.

Общее решение такого дифференциального уравнения содержит две произвольные постоянные. Если для их нахождения задать при х=x ₀ значения у(х ₀ ) искомой функции у(х) и ее производной у'(х ₀ ) , то придем к постановке задачи Коши для дифференциального уравнения (3) с двумя начальными условиями. Если же потребовать, чтобы искомое решение у(х) удовлетворяло также двум условиям:

(4),

но в двух различных точках х=а и х= b , то получим одну из возможных постановок краевой задачи, называемую двухточечной . Соотношения вида (4) называют краевыми условиями данной задачи. Геометрически постановка задачи с краевыми условиями (4) означает, что требуется найти такую интегральную кривую у(х) дифференциального уравнения (3), которая проходит через точки А(а,у _а ) и В( b ,у _b ) (рис. 3).

Возможно видоизменение постановки краевой задачи: найти такое решение y=y(x) дифференциального уравнения (3), чтобы в точках х=а и х=b были выполнены краевые условия для производной функции у(х) :

(5)

где и

Такая постановка краевой задачи с геометрической точки зрения соответствует поиску интегральной кривой у(х) дифференциального уравнения (1), пересекающей прямые х=а и х= b под заданными углами и (рис.4), где, согласно геометрическому смыслу производной функции у(х) , и .

Условия (4) и (5) принято называть краевыми условиями первого и второго рода соответственно. Очевидно, имеет смысл и постановка смешанной двухточечной краевой задачи, когда в точках х=а и х= b заданы краевые условия разного рода.

Необходимо отметить, что в отличие от задачи Коши, для которой теорема Коши гарантирует при выполнении определенных условий существование и единственность решения дифференциального уравнения, краевая задача для того же дифференциального уравнения может не иметь решения или иметь несколько решений (в том числе и бесконечное множество решений).

§3. Линейная краевая задача. Сведение ее к задаче Коши

Рассмотрим линейное неоднородное обыкновенное дифференциальное уравнение второго порядка:

(6)

Функции p ( x ), q ( x ), f ( x ) предполагаем непрерывными на отрезке [ a , b ]. Требуется найти на этом отрезке решение y ( x ) дифференциального уравнения (6), удовлетворяющее краевым условиям:

(7)

где , В – постоянные, причем такой вариант краевых условий является линейной комбинацией краевых условий первого и второго рода, его называют краевыми условиями третьего рода . В частном случае и соотношения (7) переходят в краевые условия (4) первого рода, а при , — в краевые условия (5) второго рода.

Постановка двухточечной краевой задачи в виде (6), (7) включает линейное дифференциальное уравнение второго порядка и линейные относительно значений искомой функции и ее производных краевые условия. В таком случае говорят о линейной двухточечной краевой задаче. Ее называют однородной, если f(x)=0 и А=В=0 , и неоднородной — в противном случае.

Однородная краевая задача всегда имеет тривиальное решение у(х)≡0 . Однако в прикладных исследованиях часто для однородной задачи представляют интерес решения у(х)0 . В этом случае в дифференциальных уравнениях или краевые условия (7) вводят параметр, изменяя который можно добиться, чтобы при некоторых его значениях однородная краевая задача помимо тривиального имела решение, отличное от тождественно нулевого. В некоторых случаях такой параметр уже присутствует в исходной формулировке краевой задачи и имеет вполне определенный физический, механический или геометрический смысл. Эти исключительные значения параметра, при которых однородная краевая задача имеет решение, отличное от тривиального, называют собственными значениями, а отвечающие им решения — собственными функциями этой задачи.

Нахождение собственных значений и собственных функций составляет содержание так называемой задачи на собственные значения, или задачи Штурма — Лиувилля.

Краевую задачу (6), (7) можно свести к задачам Коши для того же дифференциального уравнения (6) второго порядка и соответствующего ему однородного дифференциального уравнения:

(8)

Для этого решение краевой задачи будем искать в виде

(9)

где u = u ( x ) — нетривиальное решение однородного дифференциального уравнения (8), a v(x) — решение неоднородного дифференциального уравнения (6). Ясно, что (9) как линейная комбинация решений неоднородного дифференциального уравнения и соответствующего ему однородного уравнения также является решением дифференциального уравнения (6).

Потребуем, чтобы первое из краевых условий (7) было выполнено для у(х) при любом значении μ. Подставив (9) в это краевое условие, запишем

Это равенство будет выполнено при любом значении μ, если приравнять нулю коэффициент при μ, что приведет к двум равенствам

для выполнения которых достаточно, например, положить:

(10)

(11)

В случае  ₀ =0 вместо (11) положим

v ( a )=0 , (12)

Таким образом, u (х) есть решение задачи Коши для однородного дифференциального уравнения (8), удовлетворяющее начальным условиям (10), а v(x)- решение задачи Коши для неоднородного дифференциального уравнения (6), удовлетворяющее начальным условиям (11) или (12). При этом для любого μ функция у(х)=μu(x) + v(x) удовлетворяет первому из краевых условий (7) (при х=а ). Постоянную μ выбирают так, чтобы функция у(х) удовлетворяла второму из краевых условий (7) (при х= b ), т.е.

(13)

Если выполнено неравенство

(14)

то из (13) находим

(15)

Следовательно, краевая задача (6), (7) сведена к двум задачам Коши относительно функций u (х) и v(x) для однородного (8) и неоднородного (6) дифференциальных уравнений соответственно. Эти дифференциальные уравнения удовлетворяют всем условиям теоремы Коши о существовании и единственности решения задачи Коши, т.е. существует единственное решение u (х) дифференциального уравнения (8), удовлетворяющее начальным условиям (10), и единственное решение v(x) дифференциального уравнения (6), удовлетворяющее начальным условиям (11) или (12). Поэтому при выполнении неравенства (14) существует решение рассматриваемой линейной краевой задачи (7), (8).

Отметим, что если исходное дифференциальное уравнение (6) будет однородным, т.е. f(x)=0 , и в (7) А=0 , то в силу начальных условий (11) или (12) имеем v(a)=0 и v'(a)=0 , и поэтому v(x)=0. Тогда при выполнении неравенства (14) получим где u (х)- решение дифференциального уравнения (8), удовлетворяющее начальным условиям (10).

Сведение задачи с краевыми условиями к задаче Коши рассмотрим на примере 7, главы 2, §2.

§4. Функция Грина

Определение: Функцией Грина называется функция G ( x , s ) , определенная при и при каждом фиксированном обладающая свойствами:

1. при функция G ( x , s ) удовлетворяет уравнению:

3. при x = s функция G ( x , s ) непрерывна по x , а ее производная по x терпит разрыв первого рода со скачком, равным 1/а( s ) , т.е. G ( s +0, s )= G ( s -0, s ), (17)

Чтобы найти функцию Грина краевой задачи (16) с краевыми условиями (2), необходимо найти два решения y ₁ ( x ) и y ₂ (х) , отличные от y ( x )≡0 , уравнение (16), удовлетворяет соответственно первому и второму из краевых условий (2).

Если y ₁ ( x ) не удовлетворяет одновременно обоим краевым условиям, то функция Грина G ( x , s ) существует и ее можно представить в виде:

(18)

где функции и подбираются так, чтобы функция (18) удовлетворяла условиям (17), т.е. чтобы

Если найдена функция Грина G ( x , s ), то решение краевой задачи (16), с краевыми условиями (2) выражается формулой:

Замечание: Из определения функции Грина еще не следует ее существование для каждой краевой задачи.

Глава 2. Применение краевых задач на практике

Краевые задачи на практике применяются:

в изучении течения жидкостей в каналах;

уравнение колебаний струны;

рассеяние волн областью с неровной поверхностью

В данной главе мы рассмотрим, как можно физическую задачу свести к математической задаче.

А так же рассмотрим примеры решения уравнений для обыкновенных дифференциальных уравнений второго порядка.

§1. Краевая задача для дифференциального уравнения второго порядка в частных производных

п.1. Дифференциальные уравнения в частных производных

В главе 1 данной курсовой работы были рассмотрены дифференциальные уравнения, в которых участвовали искомые функции от одной независимой переменной, вместе с их производными. Эти уравнения носят названия обыкновенные дифференциальные уравнения.

Однако, в различных технических вопросах наиболее часто встречается искомой функция, u , от двух независимых переменных, x и t :

причем условия поставленного вопроса дают для ее определения некоторое соотношение, связывающее не только величины x , t , y , но и частные производные:

т.е. соотношение вида:

. (1)

Такое соотношение называется дифференциальным уравнением в частных производных ; порядок его определяется порядком наивысшей встречающейся в нем производной. Число независимых переменных может оказаться более двух. Для техники наибольшую важность представляют линейные уравнения в частных производных второго или высшего порядка.

Уравнение (1) называется линейным , если оно первой степени относительно искомой функции и всех производных и не содержит их произведений, т.е. это уравнение может быть записано в виде

Причем коэффициенты A , B , C , a , b , c зависят только от x и y .

Если эти коэффициенты не зависят от x и y , то уравнение (2) представляет собой линейное дифференциальное уравнение с постоянными коэффициентами .

Пусть D = B 2 -4 AC – дискриминант уравнения. В зависимости от значения D уравнение (2) относится к одному из следующих типов:

D > 0 – эллиптический тип;

D = 0 – параболический тип;

D — гиперболический тип;

D не сохраняет постоянного знака – смешанный тип.

Дифференциальное уравнение с частными производными имеет в общем случае бесчисленное множество решений. Для конкретного решения уравнения нужны дополнительные условия – начальные или краевые условия. Начальные условия характеризуют процесс в начальный момент времени. Краевые условия описывают состояние физического процесса в граничных (краевых) областях (точках).

Краевые задачи ставятся следующим образом: найти функция u , которая удовлетворяет уравнению Лапласа:

Во всех внутренних точках области S , а на границе области — некоторому условию. В зависимости от вида условия различают следующие краевые задачи:

— задача Дирихле;

— задача Неймана.

В следующем пункте представлена краевая задача для дифференциального уравнения второго порядка в частных производных, на примере уравнения колебания струны.

п.2. Вывод уравнения колебаний струны. Понятие о граничных и начальных условиях

Рассмотрим натянутую струны, т.е. тонкую гибкую упругую нить, расположенную в плоскости Oxu , которая в результате известного возмущения была выведена из положения равновесия Ox . Изучим поперечные колебания струны, полагая, что при таком колебании струны ее точки движутся перпендикулярно оси Ox .

Обозначим через u = u ( x , t ) – смещение точки струны с абсциссой х в момент времени t относительно оси Ох (рис.5).

Тогда функцией u ( x , t ) при опишется процесс колебаний струны: для любого фиксированного момента времени t = t ₁ выражением u = u ( x , t ₁ ) определяется мгновенной профиль струны.

Сделаем следующие допущения:

Предположим, что струна совершает малые колебания, т.е. ее форма в процессе колебаний незначительно отличается от прямой u =0 . Будем предполагать, что наклон касательной к графику функции u ( x , t ) , t = const , т.е. , есть малая по модулю величина по сравнению с единицей. Отсюда получаем, что и

К концам участка струны приложены направленные по касательной упругие силы натяжения (рис.5), модули которых равны: и являются практически постоянными, т.е. Т ₀ не зависит от х и t .

На струну действуют непрерывно распределенные внешние силы, перпендикулярные оси Ox , с плотностью (нагрузкой) p(x,t) , рассчитанной на единицу длины.

Вырежем из струны бесконечно малый элемент , абсциссами которого являются х и х+ dx . Воздействие отброшенной левой и правой частей струны заменим соответствующими силами натяжения. Тогда элемент можно рассматривать, как свободную материальную точку, находящуюся под действием упругих сил и внешней силы — орт оси О u .

Пусть — линейная плотность струны в точке х. Так в положении равновесия масса элемента равна , то в силу сохранения массы, элемент имеет ту же массу. Обозначим через и углы, образованные с осью Ох касательными к профилю струны в момент времени t в точках М и соответственно. Проектируя на ось Ou силы, приложенные к элементу , в силу закона Ньютона и предположения 2) получим:

(1)

Согласно предположению 1) углы и малы, поэтому:

(2)

(2*).

Для подсчета (2*) используем следующую формулу: , справедливую с точностью до бесконечно малых высших порядков.

(3)

Подставляя выражение (2) и (3) в формулу (1), получим:

(4)

Мы получили искомое уравнение малых вынужденных поперечных колебаний струны.

В случае постоянной плотности () это уравнение принимает вид:

. (5),

где , а — плотность силы, отнесенная к единице массы.

При отсутствии внешней силы ( P ( x , t ) =0) мы получаем уравнение малых свободных колебаний струны:

(6)

Уравнение (4), как показано выше, имеет бесчисленное множество решений. Поэтому для однозначной характеристики процесса колебаний необходимо к уравнению присоединить некоторые дополнительные условия, вытекающие их физического смысла данной задачи. Эти условия могут быть весьма разнообразными. В простейшем случае, как и в динамике точки, задается положение и скорость точек струны в начальный момент времени:

(7)

Эти условия, которым должно удовлетворять решение u ( x , t ) при t =0, называются начальными условиями.

Если струна ограничена, то необходимо задать условия на ее концах. В частности, для струны, концы которой x =0 и x = l закреплены,

(8)

при всяком . Условия (8) – граничные (краевые) условия.

Таким образом, физическая задача о колебаниях струны, закрепленной на концах, свелась к следующей математической задаче: найти решение u ( x , t ) уравнения (4), удовлетворяющее начальным условиям (7) и граничным условиям (8). Такая задача называется смешанной краевой задачей для уравнения колебания. К ней также можно прийти при изучении одномерных колебаний идеального газа или одномерных продольных колебаний стержня.

§2. Решение обыкновенных дифференциальных уравнений второго порядка с заданными краевыми условиями

Пример 1 . Найти решение уравнения , удовлетворяющее краевым условиям y (0)=3,

Все решения данного дифференциального уравнения выражаются формулой , где C ₁ , C ₂ – произвольные постоянные. Подберем C ₁ и C ₂ так, чтобы удовлетворялись заданные краевые условия, т.е. определим постоянные C ₁ и C ₂ из уравнений C ₁ + C ₂ =3, C ₁ + C ₂ e — C ₂ e =1. Отсюда С ₁ =1, С ₂ =2. Таким образом, решением краевой задачи является функция

Пример 2. Найти решение уравнения удовлетворяющее краевым условиям

Решение: Общее решение данного дифференциального уравнения имеет вид Условие y (0)=0 удовлетворяется при С ₁ =0, при этом y = C ₂ sinx . Если , где n – целое число, то из второго граничного условия находим: , .

Следовательно, в этом случае существует единственное решение данной краевой задачи:

.

Если , то из второго краевого условия имеет бесконечное множество решений: , где С ₂ может принимать любые значения.

В случае, если , а указанным краевым условиям не удовлетворяет ни одно решение данного дифференциального уравнения, т.е. краевая задача решений не имеет.

Пример 3: Решить краевую задачу:

Решение: Общее решение данного уравнения имеет вид:

Подставим общее решение в заданные краевые условия, получим систему уравнений относительно постоянных C ₁ и C ₂ :

Следовательно,

Пример 4: Решить краевую задачу

Решение: Общее решение данного уравнения имеет вид:

Так как то из общего решения следует, что Из краевого условия следует, что

В результате получаем:

Пример 5: Построить функцию Грина для краевой задачи

Решение: Общее решение уравнения есть Условию y (-1)=0 удовлетворяет, например, решение , а второму краевому условию – решение

Функцию Грина для указанной краевой задачи ищем в виде:

где функции и определяются из условий Отсюда

Таким образом, искомая функция Грина имеет вид:

Построив функцию Грина G ( x , s ) , запишем решение данной краевой задачи:

Пример 6: Решить краевую задачу ограничена при

Решение: Построим функцию Грина для этой задачи. Общее решение уравнения есть Решение удовлетворяет первому краевому условию, а решение удовлетворяет второму краевому условию, поэтому функцию Грина ищем в виде:

Функции и определяем из условий

, т.е. Отсюда получаем:

Искомое решение имеет вид:

Пример 7: Решить краевую задачу

На примере этой краевой задачи проиллюстрируем метод приведения краевых задач к задачам Коши. В данном случае такое приведение не эффективно, но во многих случаях, особенно в связи с методами численного решения, этот прием оказывается полезным. Найдем решение указанной краевой задачи в виде:

где соответственно решения таких задач Коши: Решив каждую из этих задач Коши, находим:

Подберем в выражении

коэффициенты  и  так, чтобы это выражение удовлетворяло краевым условиям. Подставляя в краевые условия, получаем уравнения для определения  и  :  =  , 6  +  =7.

Отсюда  =  =1. Таким образом, искомое решение имеет вид:

Теория дифференциальных уравнений является одним из самых больших разделов современной математики. Чтобы охарактеризовать ее место в современной математической науке, прежде всего необходимо подчеркнуть основные особенности теории дифференциальных уравнений, состоящей из двух обширных областей математики: теории обыкновенных дифференциальных уравнений и теории уравнений с частными производными.

Важная особенность — это непосредственная связь теории дифференциальных уравнений с приложениями. Характеризуя математику как метод проникновения в тайны природы, можно сказать, что основным путем применения этого метода является формирование и изучение математических моделей реального мира. Изучая какие-либо физические явления, исследователь прежде всего создает его математическую идеализацию или, другими словами, математическую модель, то есть, пренебрегая второстепенными характеристиками явления, он записывает основные законы, управляющие этим явлением, в математической форме. Очень часто эти законы можно выразить в виде дифференциальных уравнений. Такими оказываются модели различных явлений механики сплошной среды, химических реакций, электрических и магнитных явлений и др.

В данной курсовой работе мы познакомились с понятиями дифференциального уравнения, краевых условий; рассмотрели применение дифференциальных уравнений второго порядка к практике.

Агафонов С.А., Герман А.Д., Муратова Т.В. Диффенциальные уравнения. Математика в техническом университете. Выпуск 8. Изд-во МГТУ им.Н.Э.Баумана. 2003 – 348.

Демидович Б.П., Моденов В.П. Дифференциальные уравнения: Учебное пособие. 3-е изд.,стер. – Спб.: Издательство «Лань», 2008. – 288 с.

Егоров А.И. Обыкновенные дифференциальные уравнения с приложениями. – М.: Физматлит, 2005. – 384 с.

Камке Э. Справочник по обыкновенным дифференциальным уравнения. М., 1965. – 704 с.

Кисилев А.И., Краснов М.Л., Макаренко Г.И. Сборник задач по обыкновенным уравнениям. – М.: Изд-во «Высшая школа», 1965. – 235 с.

Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000. – 176 с.

Фихтенгольц Г.М. Математика для инженеров, часть вторая, выпуск второй. Государственное технико-теоретическое издательство Ленинград, Москва 1933 г.

🎬 Видео

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Пример 65. Решить задачу Коши (диффуры)Скачать

Краевая задача.Функция Грина.Дифференциальное ур.Скачать

Методы решения нелинейных краевых задач для ОДУСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Задача Коши для дифференциальных уравненийСкачать

Вычислительная математика. Лекция 7. Решение краевых задач для дифференциальных уравненийСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

5_1. Краевые задачи для ОДУСкачать

Вычислительная математика 14 Краевые задачиСкачать

Сведение нелинейных краевых задач для обыкновенных дифференциальных уравнений к эквивален. зад. КошиСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Численное решение задачи Коши методом ЭйлераСкачать

Кобельков Г. М. - Численные методы. Часть 2 - Краевые задачи для дифф-ых уравнений 2-го порядкаСкачать

Поле направлений дифференциального уравнения первого порядкаСкачать

Решаю высшую математику, решаю задачи качественноСкачать