Корни уравнения w3 z 0 (8 видео) | Про уравнения

Решение уравнений с комплексными числами

Итак, необходимо решить уравнение с комплексными переменными, найти корни этого уравнения. Рассмотрим принцип решения комплексных уравнений, научимся извлекать корень из комплексного числа.

Для того, чтобы решить уравнение n-й степени с комплексными числами, используем общую формулу:

где |z| — модуль числа, φ = arg z — главное значение аргумента, n — степень корня, k — параметр, принимает значения : k = .

Пример 1. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня третьей степени из комплексного числа

Воспользуемся общей формулой для вычисления корней степени n комплексного числа z. Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения.

Пример 2. Найти все корни уравнения

Найдем дискриминант уравнения:

Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта:

Найдем корни уравнения:

Ответ:

Пример 3. Найти все корни уравнения

Выразим z из уравнения:

Все корни заданного уравнения являются значениями корня четвертой степени из комплексного числа

Вновь используем общую формулу для нахождения корней уравнения n степени комплексного числа z.
n = 4 — количество корней данного уравнения. k = . Найдем модуль комплексного числа:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2, 3 найдем все 4 корня уравнения:

Пример 4. Найти корни уравнения

Решение кубического уравнения комплексными числами:

Воспользуемся общей формулой для вычисления корней степени 3 комплексного числа z.

Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:

Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения:

Домашнее задание: Самостоятельно составить и решить уравнение с комплексными числами.

Условия: переменная z должна быть «спрятана» и представлена в качестве аргумента тригонометрической функции косинуса. Чтобы привести данное уравнение к привычной форме, нужно «вытащить» z, а для этого необходимо помнить, как решаются тригонометрические уравнения,а также знать, как применять свойства логарифмической функции от комплексного числа.

После того, как мы решили тригонометрическое уравнение с комплексным числом, получаем «голый» z, который представлен в качестве аргумента обратной тригонометрической функции. Чтобы преобразовать данное выражение, нужно использовать формулу разложения арккосинуса в логарифм.

Вместо z — выражение (3i/4) и дальше все делаем по приведенной выше формуле, преобразовывая выражение под корнем, используя свойства мнимой единицы i.

Как быть далее? Теперь будем использовать формулу для решения выражения с натуральным логарифмом.

Для того чтобы найти корни логарифмического уравнения, нужно найти модуль комплексного числа |z| и его аргумент φ = arg z. По сути, перед нами чисто мнимое число.

Теперь предлагаем ознакомиться с формулами, которые могут пригодиться при решении уравнений или неравенств с комплексными числами. Это формулы, где комплексное число выступает в роли аргумента тригонометрической функции, логарифмической функции или показательной функции.

Содержание

Комплексные числа по-шагам
Результат
Примеры комплексных выражений
Правила ввода
Извлечение корня из комплексного числа
1. Определение комплексного корня
2. Формула корней
3. Геометрическая интерпретация
4. Почему корней всегда ровно n
5. Выводы
📽️ Видео

Видео:Решение, дано комплексное число z=−1+√3i. Найти корни уравнения ω3+z=0, пример 2Скачать

Комплексные числа по-шагам

Видео:Решение, дано комплексное число z=−2+2√3i. Найти корни уравнения ω3+z=0, пример 4 Высшая математикаСкачать

Результат

Примеры комплексных выражений

Деление комплексных чисел
Умножение комплексных чисел
Комплексные уравнения
Возведение комплексного числа в степень
Корень из комплексного числа

Указанные выше примеры содержат также:

квадратные корни sqrt(x),
кубические корни cbrt(x)
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
показательные функции и экспоненты exp(x)
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
натуральные логарифмы ln(x),
десятичные логарифмы log(x)
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
обратные гиперболические функции:
asinh(x), acosh(x), atanh(x), actanh(x)
число Пи pi
комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

Видео:Решение запишите число z в трех формах Найдите все корни уравнения w3−z=0 пример 7 Высшая математикаСкачать

Извлечение корня из комплексного числа

Третий урок по комплексным числам. В этом уроке вы узнаете:

Начнём с ключевого определения.

Видео:Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать

1. Определение комплексного корня

Определение. Корнем $n$-й степени из комплексного числа $z$, где $nin mathbb$, $n gt 1$, называется такое комплексное число $omega $, что

т.е. $n$-я степень числа $omega $ равна $z$.

Таких корней на множестве комплексных чисел всегда будет ровно $n$ штук. Все они обозначаются привычным знаком радикала:

Пример. Вычислить $sqrt[3]$ на множестве комплексных чисел.

Очевидно, привычная нам единица является таким корнем, потому что $<^>=-1$. Но есть ещё два корня:

Итого три корня. Как и предполагалось.

Теорема. Для любого комплексного числа $zne 0$ существует ровно $n$ комплексных чисел, каждое из которых является корнем $n$-й степени из числа $z.$

Все эти корни считаются по следующей формуле.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

2. Формула корней

Теорема. Пусть комплексное число записано в тригонометрической форме:

[z=left| z right|cdot left( cos varphi +isin varphi right)]

Тогда все корни степени $n$ из этого числа можно найти по формуле:

По сути, эта теорема является обратной к формуле Муавра:

Почему степень всегда одна, а корней несколько — об этом в конце урока. Сейчас для нас главное — алгоритм извлечения корня из комплексного числа. Он состоит из четырёх шагов:

Перевести комплексное число в тригонометрическую форму;
Записать общую формулу корня степени $n$;
Подставить в эту формулу $k=0$, затем $k=1$ и так до $k=n-1$.
Получим $n$ комплексных корней. Вместе они и будут ответом.

В ответе всегда будет набор из $n$ чисел. Потому что невозможно однозначно извлечь корень из комплексного числа $zne 0$.

Представим число $-8i$ в тригонометрической форме:

[begin -8i &=0+left( -8 right)cdot i= \ & =8cdot left( 0+left( -1 right)cdot i right)= \ & =8cdot left( cos left( -frac right)+isin left( -frac right) right) end]

Запишем формулу корней в общем виде:

[sqrt[3]=2cdot left( cos left( -frac right)+isin left( -frac right) right)=sqrt-i]

В ответе нужно указать все три числа: $-2i$; $sqrt-i$; $-sqrt-i$.

Ещё раз: подставляя разные $k$, мы будем получать разные корни. Всего таких корней будет ровно $n$. А если взять $k$ за пределами диапазона $left$, то корни начнут повторяться, и ничего нового мы не получим.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

3. Геометрическая интерпретация

Если отметить на комплексной плоскости все значения корня $n$-й степени из некоторого комплексного числа $zne 0$, то все они будут лежать на окружности с центром в начале координат и радиусом $R=sqrt[n]$. Более того: эти точки образуют правильный $n$-угольник.

Отметить на комплексной плоскости все числа вида $sqrt[3]$.

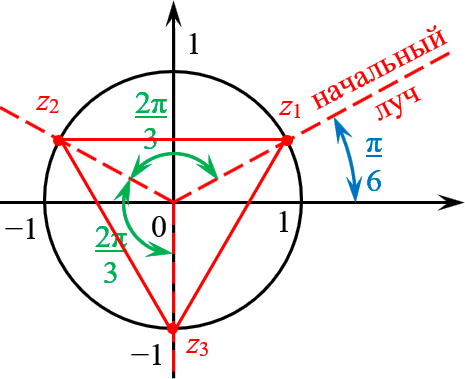
Представим число $z=i$ в тригонометрической форме:

[begin z & =1cdot left( 0+icdot 1 right)= \ & =1cdot left( cos frac+isin frac right) end]

Формула комплексных корней:

[sqrt[3]=1cdot left( cos left( frac+frac right)+isin left( frac+frac right) right)]

Это три точки $<_>$, $<_>$ и $<_>$ на окружности радиуса $R=1$:

Получили правильный треугольник. Его первая вершина лежит на пересечении окружности радиуса 1 и начального луча, который образован поворотом оси $OX$ на угол $/;$.

Рассмотрим более сложный пример:

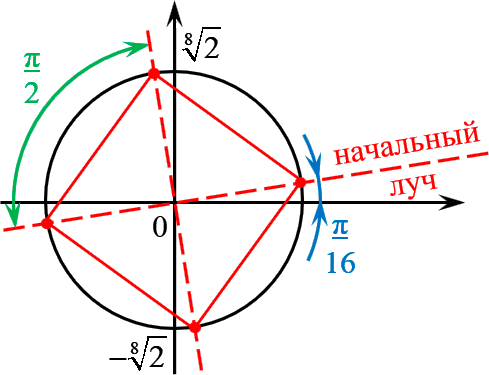
Отметить на комплексной плоскости все числа вида $sqrt[4]$.

Сразу запишем формулу корней с выделением начального луча:

[sqrt[4]=sqrt[8]cdot left( cos left( frac+frac right)+isin left( frac+frac right) right)]

Отмечаем эти точки на комплексной плоскости. Радиус окружности $R=sqrt[8]$, начальный луч $/;$:

И вновь всё чётко: четыре точки — правильный четырёхугольник, т.е. квадрат. С отклонением начального луча $/;$.

Ну и ещё один пример — вновь без промежуточных вычислений. Только формулировка задачи, формула корней и окончательный чертёж:

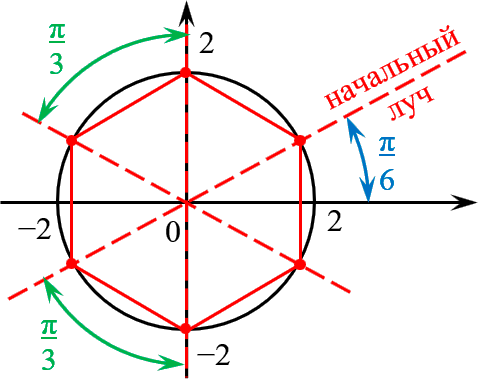
Отметить на комплексной плоскости все числа вида $sqrt[6]$.

Формула корней с выделением начального луча:

[sqrt[6]=2cdot left( cos left( frac+frac right)+isin left( frac+frac right) right)]

Получили правильный шестиугольник со стороной 2 и начальным лучом $/;$.

Таким образом, мы получаем «графический» алгоритм извлечения корня $n$-й степени из комплексного числа $zne 0$:

Перевести число в тригонометрическую форму;
Найти модуль корня: $sqrt[n]$ — это будет радиусом окружности;
Построить начальный луч с отклонением $varphi =/;$;
Построить все остальные лучи с шагом $/;$;
Получим точки пересечения лучей с окружностью — это и есть искомые корни.

Такой алгоритм прекрасно работает, когда аргумент исходного числа и отклонение начального луча $varphi $ — стандартные «табличные» углы вроде $/;$. На практике чаще всего именно так и бывает. Поэтому берите на вооружение.:)

Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

4. Почему корней всегда ровно n

С геометрической точки зрения, всё очевидно: если мы будем последовательно зачёркивать вершины правильного $n$-угольника, то ровно через $n$ шагов все вершины будут зачёркнуты. И для дальнейшего зачёркивания придётся выбирать вершину среди уже зачёркнутых.

Однако рассмотрим проблему с точки зрения алгебры. Ещё раз запишем формулу корня $n$-й степени:

Последовательно подставим в эту формулу указанные значения параметра $k$:

Очевидно, последняя строка получена при $k=n-1$. Подставим теперь $k=n$:

Поскольку синус и косинус — периодические функции с периодом $2pi $, $<_>=<_>$, и далее корни будут повторяться. Как мы и заявляли в самом начале урока.

Видео:Комплексные корни квадратных уравнений. 11 класс.Скачать

5. Выводы

Ключевые факты из урока.

Определение. Корень степени $n$ из комплексного числа $z$ — это такое число $omega $, что $<^>=z$.

Обозначение. Для обозначения комплексных корней используется знакомый знак радикала: $omega =sqrt[n]$.

Замечание. Если $zne 0$, таких чисел корней будет ровно $n$ штук.

Алгоритм нахождения корней состоит из двух шагов.

Шаг 1. Представить исходное число в тригонометрической форме:

[z=left| z right|cdot left( cos varphi +isin varphi right)]

Шаг 2. Воспользоваться формулой Муавра для вычисления корней:

Все полученные корни лежат на окружности радиуса $sqrt[n]$ с центром в начале координат и являются вершинами правильного $n$-угольника. Первая вершина лежит на т.н. «начальном луче», который отклонён от положительной полуоси $OX$ на угол $/;$. Остальные вершины обычно легко находятся из соображений симметрии с помощью циркуля и линейки.

Геометрическую интерпретацию можно использовать для быстрого «графического» извлечения корней. Но это требует практики и хорошего понимания, что именно и зачем вы делаете. Технология такого извлечения корней описана выше в разделе «Геометрическая интерпретация».

Всё. В следующем уроке начнём решать уравнения в комплексных числах.:)