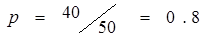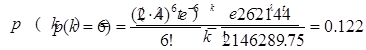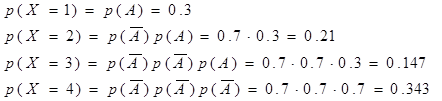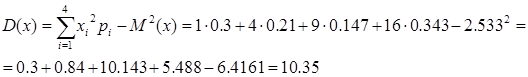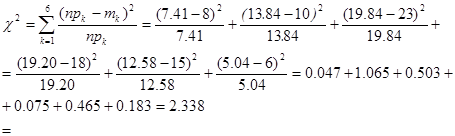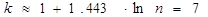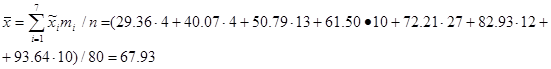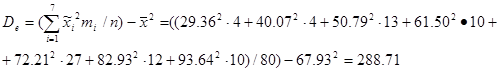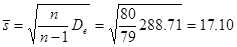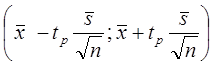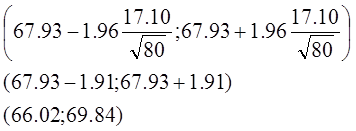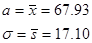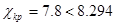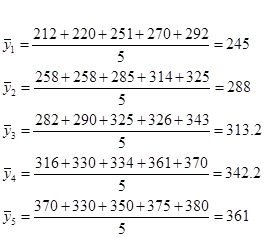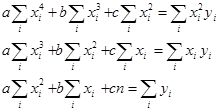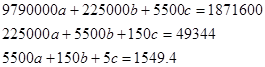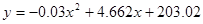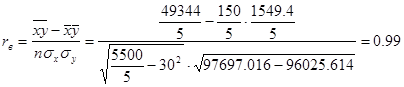| Название: Формула Бернулли, Пуассона. Коэффициент корреляции. Уравнение регрессии Раздел: Рефераты по математике Тип: контрольная работа Добавлен 01:29:20 14 мая 2003 Похожие работы Просмотров: 750 Комментариев: 21 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
Если же происходит событие Н2 то во второй урне станет 6 черных и 4+1=5 белых шаров. Вероятность наступления А
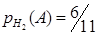 |
По формуле полной вероятности вычислим вероятность события А (из второй урны вынут черный шар)
 |
Видео:10. Уравнения БернуллиСкачать

Ответ: 0,60
5 . Студент знает 40 из 50 вопросов программы. Найти вероятность того, что студент знает 2 вопроса, содержащиеся в его экзаменационном билете.
Для каждого вопроса вероятность того что студент его знает, одинакова
Найдем вероятность того, что в двух испытаниях событие А (студент знает вопрос) произойдет 2 раза по формуле Бернулли
 |
Ответ: 0,64
11 . Среднее число вызовов, поступающих на АТС в 1 мин., равно четырем. Найти вероятность того, что за 2 мин. поступит: 1) 6 вызовов; 2) менее шести вызовов; 3) не менее шести вызовов. Предполагается, что поток вызовов – простейший.
Решение
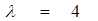
По формуле Пуассона, вероятность того что за время t поступит k вызовов, равна
 |
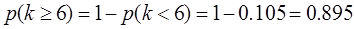 |
3)
15 . Среднее число самолетов, прибывающих в аэропорт за 1 мин, равно трем. Найти вероятность того, что за 2 мин прибудут: 1) 4 самолета; 2) менее четырех самолетов; 3) не менее четырех самолетов.
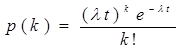 |
По формуле Пуассона, вероятность того что за время t поступит k вызовов, равна
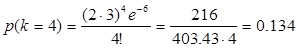
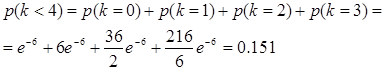 |
2)
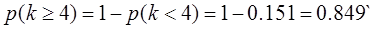
21-30 . Для дискретной случайной величины Х, определенной в задаче:
1).написать ряд распределения; 2).построить многоугольник распределения;
3).вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение; 4).построить интегральную функцию распределения.
21. Вероятность того, что в библиотеке необходимая книга свободна, равна 0,3. В городе 4 библиотеки. СВ Х – число библиотек, которые посетит студент в поисках необходимой книги.
Случай ная величина Х может принимать такие значения
Х=1 – если студент найдет книгу в первой же библиотеке
Х=2 –если в первой не найдет а найдет во второй
Х=3- если не найдет в первой и второй а найдет в третьей
Х=4- если не найдет ни в первой, ни во второй, ни в третьей.
Найдем их вероятности.
Пусть событие А состоит в том что книга найдена. Р(А)=0,3.
Не найдена – вероятность противоположного события равна
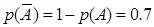
| Х | 1 | 2 | 3 | 4 |
| Р | 0,3 | 0,21 | 0,147 | 0,343 |
2) См. рисунок 1(21)
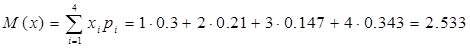
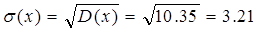 |
Среднеквадратическое отклонение
По таблицам для критерия Пирсона найдем критическую точку для количества степеней свободы k=6-1-2=3 и q=0.05
Отсюда следует, что различия между теоретическими и опытными частотами случайны и гипотезу о нормальном распределении следует принять.
45.
24, 99, 28, 68, 72, 81, 85, 93, 29, 36, 32, 48, 72, 52, 62, 60, 40, 85, 68, 76,
64, 52, 60, 76, 56, 60, 64, 68, 72, 76, 72, 68, 72, 85, 68, 72, 73, 98, 44, 51,
48, 52, 97, 56, 84, 81, 97, 62, 64, 56, 93, 86, 69, 89, 64, 81, 56, 72, 72, 81,
68, 76, 85, 70, 81, 72, 68, 71, 72, 93, 76, 92, 72, 93, 65, 55, 84, 36, 48, 52.
2) Объем выборки n=80
Наименьшее значение признака Х
| MIN: | 24 |
| MAX: | 99 |
Определим оптимальное число интервалов разбиения по формуле
| Число интервалов: | 7,00 |
| Шаг интервала h=(99-24)/7= | 10,71 |
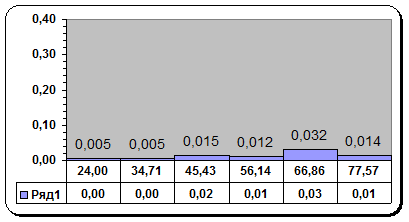
Составим интервальный вариационный ряд
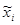 Интервальный ряд Интервальный ряд | Колич. Элементов m(i) | |||
| 24,00 | 34,71 | 4 | 0,05 | 29,36 |
| 34,71 | 45,43 | 4 | 0,05 | 40,07 |
| 45,43 | 56,14 | 13 | 0,16 | 50,79 |
| 56,14 | 66,86 | 10 | 0,13 | 61,50 |
| 66,86 | 77,57 | 27 | 0,34 | 72,21 |
| 77,57 | 88,29 | 12 | 0,15 | 82,93 |
| 88,29 | 99,00 | 10 | 0,13 | 93,64 |
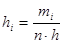
 |
3)Точечной оценкой математического ожидания является эмпирическая средняя
Точечной оценкой генеральной дисперсии является дисперсия эмпирическая
Точечная оценка генерального среднего квадратического отклонения
Исправленное среднее квадратическое отклонение
4)Доверительный интервал для неизвестного математического ожидания
имеет вид (при надежности p=0.95)
Доверительный интервал для оценки математического ожидания имеет вид
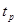
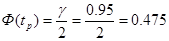 |
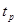 |
По таблицам значений функции Лапласа находим =1,96
Доверительный интервал имеет вид
7)
Предположим, что количественный признак Х имеет нормальное распределение и вычислим теоретические частоты.
Вероятность попадания в интервал для нормально распределенной случайной величины
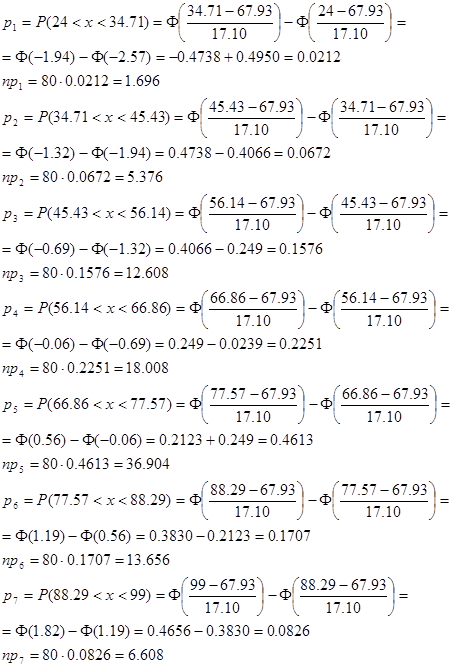 |
Для более точного применения критерия Пирсона требуется чтобы теоретические частоты были>5. Это не выполняется для интервала 1, который объединяем с соседним. Теперь количество интервалов равно 6. Найдем величину уклонения
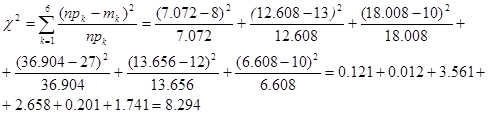 |
По таблицам для критерия Пирсона найдем критическую точку для количества степеней свободы k=6-1-2=3 и q=0.05
Отсюда следует, что различия между теоретическими и опытными частотами значимы и гипотезу о нормальном распределении следует отклонить..
Для установления корреляционной зависимости между величинами
X и Y (где Y- случайная величина, X- неслучайная величина) проведены
эксперименты, результаты которых представлены в таблице.
Требуется: 1. Найти условные средние 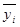
регрессии Y по X (ломаную). 2. Найти уравнение регрессии Y по X
методом наименьших квадратов, принимая в качестве сглаживающей
линии параболу 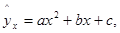
с эмпирической линией регрессии. 3. Оценить тесноту корреляционной
зависимости Y по X. 4. Проверить адекватность уравнения регрессии Y по X.
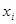 | 10 | 20 | 30 | 40 | 50 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
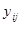 |
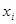 | 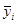 | 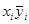 | 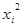 | 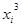 | 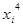 | 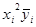 | Y(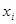 ) ) | |
| 1 | 10 | 245 | 2450 | 100 | 1000 | 10000 | 24500 | 246,64 |
| 2 | 20 | 288 | 5760 | 400 | 8000 | 160000 | 115200 | 284,26 |
| 3 | 30 | 313,2 | 9396 | 900 | 27000 | 810000 | 281880 | 315,88 |
| 4 | 40 | 342,2 | 13688 | 1600 | 64000 | 2560000 | 547520 | 341,5 |
| 5 | 50 | 361 | 18050 | 2500 | 125000 | 6250000 | 902500 | 361,12 |
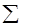 | 150 | 1549,4 | 49344 | 5500 | 225000 | 9790000 | 1871600 |
Получаем систему уравнений
Решение системы: a=-0.03; b=4.662; c=203.02
Получаем уравнение кривой
Подставляя в уравнение поочередно значения х, получаем соответствующие точки параболы, которые и наносим на график.(рис 3(51))
3. Найдем значение коэффициента корреляции
Отсюда можно сделать вывод что зависимость прямая сильная., тк
Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Контрольная работа «Испытания Бернулли»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Будут ли испытаниями Бернулли следующие серии опытов (если да, то найдите р и q в тех случаях, когда это возможно):
а) десятикратное бросание кубика; успех выпадение шестерки;
б) ответы у доски на уроках математики в течение месяца; успех получение пятерки;
в) проверка лампочек при их продаже в магазине; успех лампочка бракованная;
г) вытаскивание 10 карт из колоды без возвращения; успех вытаскивание красной масти.
б)да, р=1/5, g=4/5 Так как ученик на уроке может получить отметки1;2;3;4;5
г) нет, так как результаты опыта зависимы
Какова вероятность, что при бросании шести кубиков выпадет хотя бы одна шестерка?
Вподъезде горит 5 лампочек. Вероятность, что любая лампочка не сгорит в течение ближайшего месяца, равна 0,2. Какова вероятность, что в течение месяца
а) сгорят все лампочки;
б) сгорит ровно одна лампочка;
в) останутся гореть, по крайней мере, 3 лампочки.
то есть0 лампочек не сгорит
б) т.е. останется 4 лампочки
в) по крайней мере,три,т.е.3 или 4 лампочки
Вратарь футбольной команды отражает в среднем каждый третий пенальти. Сколько пенальти из пяти он отразит, скорее всего? С какой вероятностью?
Нахожу ожидаемое число удач при n =5 с вероятностью успеха р=1/3.
Завод отправил заказчику 10000 стандартных изделий. Средняя доля изделий, повреждаемых при транспортировке, составляет 0,02%. Найдите вероятность того, что в этой партии будет повреждено.
а) ровно 3 изделия;
б) не более 3 изделий.
1. а ) Вероятность того , что изделие будет повреждено при транспортировке , равна
мала , n=10000 — велико и
n p 10000 0,0002 2 10 , следует
применить формулу Пуассона : P
Для события «будет повреждено не более 3 из 10000», p = 0,0002 и P10000(m ≤ 3) = P0,10000+ P1,10000+ P2,10000+ P3,10000 = 0,1353+0,2707+0,2707+0,1805 = 0,8572.
Краткое описание документа:
Контрольная работа с решениями по теме «Испытания Бернулли». Рассмотрены 5 заданий на вероятность с решениями. Материал может пригодится при подготовке к ЕГЭ (задание 4) и изучении темы «Элементы теории вероятностей», а так же для внеурочных занятий. По данной теме очень интересный материал на курсах Инфоурока!
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 932 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 682 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 308 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Закон БернуллиСкачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 574 134 материала в базе
Другие материалы
- 27.11.2017
- 251
- 0
- 27.11.2017
- 303
- 0
- 27.11.2017
- 216
- 0
- 27.11.2017
- 219
- 0
- 27.11.2017
- 167
- 0
- 26.11.2017
- 1386
- 2
- 26.11.2017
- 398
- 1
- 26.11.2017
- 1450
- 37
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 27.11.2017 3250
- DOCX 21 кбайт
- 98 скачиваний
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Затравкина Татьяна Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 4 месяца
- Подписчики: 0
- Всего просмотров: 16553
- Всего материалов: 11
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Контрольная работа. Уравнения с МОДУЛЕМСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Инфоурок стал резидентом Сколково
Время чтения: 2 минуты
Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.
Время чтения: 2 минуты
Минпросвещения подключит студотряды к обновлению школьной инфраструктуры
Время чтения: 1 минута
В Курганской области дистанционный режим для школьников продлили до конца февраля
Время чтения: 1 минута
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
Объявлен конкурс дизайн-проектов для школьных пространств
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

контрольная работа по гидравлике. Контрольная работа Определение слагаемых уравнения Д. Бернулли при движении жидкости в трубопроводе Цель работы
| Название | Контрольная работа Определение слагаемых уравнения Д. Бернулли при движении жидкости в трубопроводе Цель работы |
| Анкор | контрольная работа по гидравлике |
| Дата | 14.09.2020 |
| Размер | 1.54 Mb. |
| Формат файла |  |
| Имя файла | контрольная работа по гидравлике.docx |
| Тип | Контрольная работа #137821 |
| Подборка по базе: Практическая работа ИБ1.docx, Практическая работа № 2.docx, Практические работа 6.docx, Практическая работа 1.docx, Самостоятельная работа 4-2. История.docx, Практическая работа 10.docx, Самостоятельная работа 4-3. История.docx, Лабораторная работа 1..docx, Контрольная работа по экономике 5 курс.doc, Лабораторная работа №2 208.docx Кафедра «Теоретические основы теплотехники и гидромеханика» Видео:Закон БернуллиСкачать  Цель работы:
Видео:Урок 134. Применения уравнения Бернулли (ч.1)Скачать  Порядок выполнения работы
🔍 ВидеоДифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать  ФЕВРАЛЬ 2024 БУДЕТ ЗАКЛЮЧИТЕЛЬНЫМ! ПРЕДСКАЗАНИЕ ИНДИЙСКОГО МАЛЬЧИКАСкачать  Эффект Магнуса и уравнение БернуллиСкачать  Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать  Галилео. Эксперимент. Закон БернуллиСкачать  Уравнения Бернулли. Дифференциальны уравненияСкачать  Математика без Ху!ни. Теория вероятностей. Схема БернуллиСкачать  Закон БернуллиСкачать  Уравнение Бернулли. Практическая часть. 10 класс.Скачать  Уравнение Бернулли гидравликаСкачать  18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать  |

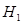 Решение
Решение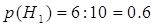
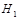 Пусть гипотезы и состоят в том что:
Пусть гипотезы и состоят в том что: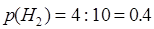 Из первой урны извлекли черный шар, вероятность
Из первой урны извлекли черный шар, вероятность