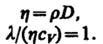Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Описание презентации по отдельным слайдам:
Лекция 22-23. Явления переноса Макроскопические явления переноса. Внутреннее трение (перенос импульса): закон Ньютона — Стокса. Теплопроводность: закон Фурье. Диффузия: закон Фика. Уравнение переноса. Явление переноса в газах. Связь коэффициентов переноса с молекулярно-кинетическими характеристиками газа. Связь между коэффициентами переноса и их зависимость от температуры и плотности. Особенности процессов переноса в жидких и твердых телах.
Явления переноса Термодинамика — системы в равновесном состоянии. Система в неравновесном состоянии — переход к равновесному состоянию посредством явлений переноса. Время достижения равновесия — время релаксации. Рассмотрим три основных явления переноса – внутреннее трение (вязкость), теплопроводность и диффузию. Вязкость. При относительном движении различных частей фазы возникают факторы, стремящиеся уменьшить относительную скорость, т. е. возникают силы торможения, или вязкость. Механизм этих сил в газах сводится к обмену импульсом упорядоченного движения между различными слоями газа, т. е. к переносу импульса упорядоченного движения. Возникновение сил трения в жидкостях также обусловлено процессом переноса импульса упорядоченного движения молекул.
Явления переноса Теплопроводность. В состоянии равновесия температура Т во всех точках системы одинакова. При отклонении температуры от равновесного значения в некоторой области в системе возникает движение теплоты в таких направлениях, чтобы сделать температуру всех частей системы одинаковой. Связанный с этим движением перенос теплоты называется теплопроводностью. Диффузия. В состоянии равновесия плотность каждой из компонент во всех точках фазы одинакова. При отклонении плотности от равновесного значения в некоторой области в системе возникает движение компонент вещества в таких направлениях, чтобы сделать плотность каждой из компонент постоянной по всему объему системы. Связанный с этим движением перенос вещества компонент, составляющих фазу, называется диффузией.
Явления переноса Внутреннее трение: закон Ньютона — Стокса
Явления переноса Теплопроводность: закон Фурье
Явления переноса Диффузия: закон Фика Бинаная смесь. Через перпендикулярную к z площадку S устанавливается поток молекул 1-го сорта массы M1:
Явления переноса Уравнение переноса. Явление переноса в газах. Общее уравнение переноса. Пусть G характеризует некоторое молекулярное свойство, отнесенное к одной молекуле. Этим свойством может быть энергия, импульс, концентрация, электрический заряд и т. д. При наличии градиента G имеет место движение G в направлении его уменьшения. Пусть ось X направлена вдоль градиента G. Среднее расстояние, пробегаемое молекулами, пересекающими площадку dS после последнего столкновения, равно 2 /3. Эта величина в большинстве случаев достаточно мала и G на расстоянии 2 /3 от площадки dS можно представить в виде
Явления переноса Среднее расстояние вдоль оси Z, которое проходят молекулы, пересекающие площадку dS после последнего столкновения dN — число молекул, пересекших площадку dS и на пути от элемента объема dV не испытавших ни одного последующего столкновения Поток числа молекул в направлении оси X равен n0 /4. Следовательно, поток G сквозь площадку dS в направлении отрицательных и положительных значений оси X равны
Явления переноса Полный поток в положительном направлении оси X в точке х имеет вид Уравнение является основным уравнением процессов переноса количества G. Теплопроводность. G — средняя энергия теплового движения, приходящаяся на одну молекулу. IG — поток теплоты, который будем обозначать Iq. Из теоремы о равнораспределении энергии по степени свободы
Явления переноса Уравнение переноса (уравнение Фурье или закон Фурье) где — теплопроводность, — соответственно плотность Главное изменение теплопроводности при фиксированной концентрации частиц газа проистекает из-за различия в средней скорости . Благодаря этому легкие газы обладают начительно большей теплопроводностью, чем тяжелые. Кислород — 0,024 Вт/(м • К), водород — 0,176 Вт/(м • К). и удельная теплоемкость газа при постоянном объеме.
Явления переноса Поскольку n0 = 1/σ не зависит от давления, a
Т1/2 и также не зависит от давления, можно заключить, что теплопроводность не зависит от давления, что хорошо подтверждается экспериментом, и увеличивается приблизительно прямо про- пропорционально корню квадратному из температуры. Здесь использовано выражение «приблизительно» потому, что с увеличением температуры поперечное сечение σ несколько уменьшается.
Явления переноса Вязкость. В результате теплового движения молекулы перелетают из одного слоя газа в другой, перенося при этом свой импульс упорядоченного движения из одного слоя в другой. В результате обмена молекулами между слоями, движущимися с различ- различными скоростями, импульс упорядоченного движения быстрее движущегося слоя уменьшается, а медленнее движущегося — увеличивается. Это означает, что быстрее движущийся слой тормозится, а медленнее движущийся ускоряется. В этом и состоит механизм возникновения силы внутреннего трения между слоями газа, движущимися с различными скоростями.
Явления переноса Сила трения, τ, отнесенная к площади трущихся поверхностей газа, равна потоку импульса упорядоченного движения в перпендикулярном скорости направлении. — динамическая вязкость (Дж. Максвелл, 1860 г.) динамическая вязкость не зависит от давления и растет в основном пропорционально корню квадратному от температуры, (небольшой рост связан с уменьшением σ при росте температуры.
Явления переноса Независимость динамической вязкости, т. е. силы трения, от давления и, следовательно, от плотности газа. Длина свободного пробега изменяется обратно пропорционально давлению, а концентрация молекул — прямо пропорционально. Переносимый каждой молекулой импульс упорядоченного движения прямо пропорционален длине свободного пробега, т. е. обратно пропорционален давлению. Поскольку концентрация молекул, переносящих импульс, прямо пропорциональна давлению, получается, что суммарный переносимый молекулами импульс, отнесенный к промежутку времени и объему, не зависит от давления (подтверждается экспериментально). Единицей динамической вязкости является 1 Па∙с. Динамическая вязкость газов при температуре 20°С и атмосферном давлении имеет порядок 10-5 Па∙с. Кинематическая вязкость:
Явления переноса Самодиффузия. Пусть молекулы равномерно заполняют некоторый объем. Допустим, что все молекулы одинаковы по всем своим механическим и динамическим параметрам, однако могут отличаться по некоторому признаку, не оказывающему влияние ни на взаимодействие между молекулами, ни на их движения. Таким образом, переносимым признаком в этом случае является просто идентичность молекул, т. е. признак их индивидуальной идентификации. Назовем условно этот признак «цветом» и будем считать, что имеются белые и черные молекулы. Предположим, что концентрация белых и черных молекул в пространстве неоднородна. Очевидно, что в состоянии равновесия как «черный», так и «белый» сорт молекул должен равномерно заполнить весь объем. Поэтому при неоднородном распределении начнется выравнивание концентраций в результате столкновений между молекулами. Переносимым количеством в этом случае является концентрация рассматриваемого сорта молекул.
Явления переноса Пусть концентрация первого сорта молекул n1(х). Учитывая, что G в уравнении переноса есть характеристика переносимого количества, отнесенная к одной молекуле, имеем где n0 — равновесная концентрация. Уравнение переноса принимает вид где — коэффициент диффузии.
Явления переноса При фиксированной температуре =const, а l
1/р. Следовательно, при T=const D
1/р. С другой стороны, при фиксированном давлении l
Т, a Следовательно, при p=const D
Т3/2. Эти заключения были тщательно проверены в экспериментах. Соотношение Dp = const, соблюдается в довольно широком интервале давлений для не очень плотных газов с точностью до нескольких десятков процентов. В зависимости от температуры D растет несколько быстрее, чем пропорционально Т3/2. Это объясняется тем, что при росте Т несколько уменьшается поперечное сечение, что приводит к дополнительному увеличению длины свободного пробега. Коэффициент диффузии для кислорода и азота в воздухе при нормальных условиях имеет порядок 10-5 м2/с.
Явления переноса Связь между коэффициентами, характеризующими уравнение переноса. где cv— удельная теплоемкость при постоянном объеме, ρ — плотность вещества. Наличие этой связи между коэффициентами процессов переноса обусловлено одинаковостью физической природы процессов переноса.
Явления переноса Взаимодиффузия в газе из различных молекул. Если имеется два сорта молекул, различающихся динамическими свойствами и характером взаимодействия, то процесс диффузии значительно усложняется. Пусть для определенности имеются тяжелые и легкие молекулы. Обозначим концентрации молекул n1 и n2. Условие постоянства давления и температуры по всему объему по закону Дальтона имеет вид Для диффузионных потоков молекул каждого сорта
Явления переноса Очевидно, что в общем случае D1 и D2 не равны, поэтому диффузионные потоки не компенсируют друг друга, вследствие чего должно нарушиться постоянство давления по объему газа. Поэтому наряду с диффузионными потоками должен возникнуть гидродинамический поток, т. е. движение газа как целого, такой, чтобы сохранить постоянство давлений. Обозначая v — гидродинамическую скорость потока газа как целого, можно условие неизменности давления записать в виде Отсюда
Явления переноса Поэтому полный поток первой компоненты, являющийся суммой диффузионного и гидродинамического потоков этой компоненты, равен где Таким образом, задача сводится к громоздким вычислениям средних длин свободных пробегов. Дж. Максвелл и Ц. Стефан для вычисления этих величин в модели жестких, абсолютно упругих шаров предложили следующие формулы:
Явления переноса Физические явления в разреженных газах Вакуум. При уменьшении давления длина свободного пробега увеличивается. Когда она становится равной линейным геометрическим размерам объекта, то молекулы сталкиваются лишь со стенками сосуда (если объем ограничен стенками) и практически не сталкиваются друг с другом. Такая ситуация называется вакуумом. Понятие вакуума относительно. Чем больше линейные размеры области, тем при меньшем давлении он достигается. При нормальных атмосферных условиях l
10-6 см. Теплопередача при малых давлениях. Столкновения между молекулами практически отсутствуют, молекулы являются переносчиками энергии от более горячих стенок к более холодным. Правильнее говорить о теплопередаче газом теплоты, поскольку никакого градиента температур в объеме сосуда нет.
Явления переноса Зависимость способности к теплопередаче от давления у газа другая, чем зависимость теплопроводности от давления. При высоком давлении теплопроводность не зависит от давления, теплопередача же при низком давлении увеличивается с ростом давления, поскольку увеличивается частота ударов молекул о стенки сосудов. И наоборот, теплопередача уменьшается при уменьшении давления до сколь угодно малых значений. Примером практического использования этого являются сосуды Дьюара. В полых стенках создаются условия вакуума с достаточно низкой теплопередачей. Диффузия при малых давлениях. Поскольку столкновений между молекулами в объеме практически нет, передача молекулярных признаков происходит со скоростью движения молекул, т. е. очень быстро. Время уравнивания концентраций даже в очень больших объемах является малым.
Явления переноса Трение при малых давлениях. Если имеются две твердые поверхности, движущиеся друг относительно друга, причем между поверхностями находится газ в условиях вакуума, то между поверхностями возникают силы трения, стремящиеся затормозить более быстро движущуюся и ускорить медленнее движущуюся поверхности. Это явление похоже по внешнему виду на возникновение аналогичных сил при достаточно высоком давлении, но механизм совершенно другой. В условиях вакуума между движущимися поверхностями не возникает слоев газа, движущихся поступательно друг относительно друга, в результате чего возникает сила внутреннего трения, передающаяся от слоя к слою. При столкновении с движущейся поверхностью молекула приобретает соответствующий импульс упорядоченного движения и, пролетев без столкновений пространство между поверхностями, обменивается импульсом своего упорядоченного движения с другой поверхностью.
Явления переноса Импульс, переданный поверхности молекулами в каждую секунду, численно равен силе трения. Таким образом, в условиях вакуума отсутствует внутреннее трение в газе в том смысле, в каком оно существует при более высоком давлении, но имеется взаимное трение движущихся друг относительно друга поверхностей. Сосуды, сообщающиеся через пористую перегородку. Размеры пор в пористой перегородке могут быть столь малыми, что в них соблюдаются условия вакуума уже при нормальном атмосферном давлении. Если по разные стороны пористой перегородки имеется один и тот же газ и поддерживаются различные температуры, то устанавливается равновесное состояние, при котором давления по разные стороны пористой перегородки различны.
Явления переноса В условиях равновесия число молекул, перелетающих из одной половины в другую через пористую перегородку, равно числу молекул, пролетающих через пористую перегородку в обратном направлении. Поскольку сами поры молекулы проходят без столкновений, то это условие имеет вид где Sэф — эффективная суммарная «площадь» пор в перегородке. Учитывая, что т. е. там, где температура больше, давление также больше. Такая ситуация при нормальных условиях невозможна, поскольку возникшие при разности давлений гидродинамические потоки быстро выравнивают давление.
Явления переноса Явления переноса в твердых телах Диффузия. В жидкостях и твердых телах также имеют место явления переноса, но механизм этих явлений отличается от механизма в газах. Это обусловлено тем, что, во-первых, в жидкостях и твердых телах теряет смысл представление о длине свободного пробега и, во-вторых, силы взаимодействия между молекулами очень велики и оказывают постоянное влияние на их движение. В твердых телах наблюдается как самодиффузия, так и взаимодиффузия. Наиболее наглядно это демонстрируется фактом взаимопроникновения вещества двух тел, находившихся достаточно долгое время в тесном контакте друг с другом.
Явления переноса Самодиффузия осуществляется главным образом с помощью трех следующих механизмов. 1. Если в узле кристаллической решетки имеется вакансия, то один из соседних атомов может совершить переход из своего узла в вакантный узел. Этот переход эквивалентен движению вакансии. Для того чтобы имел место процесс самодиффузии, обусловленный движением вакансий, необходимо, чтобы в решетке присутствовало неравномерное распределение вакансий, т. е. градиент плотности вакансий. При создании вакансий важную роль играют дислокации. Для осуществления диффузии посредством движения вакансий необходимо одновременное наличие двух условий: существования вакансии и образования у одного из соседних атомов достаточно большой энергии колебания, чтобы он смог покинуть свой узел.
Явления переноса 2. Если у атома в узле кристаллической решетки образовалась достаточно большая энергия колебаний, то он покидает свой узел. Если по соседству нет вакансии, то он располагается между узлами и затем движется в междоузлиях. 3. Может произойти обмен атомами в соседних узлах решетки. Диффузия в твердом теле описывается уравнением Фика, однако коэффициент диффузии D определяется другими факторами. определяется другими факторами. Главную роль в диффузии играет движение вакансий. Обозначим: τ — среднее время «оседлой» жизни атома в узле решетки, — смещение атома при перескоке (период решетки). Средняя скорость движения атомов при перескоках = / . Атом может равновероятно сделать перескок по шести независимым направлениям. Следовательно,
Явления переноса Для осуществления перескока необходимо, чтобы имелась вакансия и соседний атом имел достаточную энергию для совершения перескока в вакансию. Обозначим εв энергию, при приобретении которой атом покидает обязательно свой узел, в результате чего образуется вакансия. В соответствии с распределением Гиббса вероятность образования вакансии равна С другой стороны, обозначая εп энергию, которую должен иметь атом, чтобы совершить перескок в имеющуюся вакансию, можно для вероятности перескока при наличии вакансии написать
Явления переноса Отсюда для вероятности того, что одновременно будет иметься вакансия и совершится перескок в эту вакансию, можем написать W — энергия активации диффузии. Очевидно, что частота перескоков прямо пропорциональна вероятности перескока, т. е. вещества. Коэффициент диффузии в твердых телах очень мал (неизмеримо меньше, чем для газов). Например, для золота он равен 10-35 м2/с, в то время как для кислорода в атмосфере он равен примерно 10-5 м2/с. — постоянная, определяемая свойствами
Явления переноса Теплопроводность. Она осуществляется не тем, что молекулы перемещаются в твердом теле, а посредством взаимодействия между молекулами, в результате которого их тепловое движение приобретает коллективный характер. где vзв — скорость звука в твердом теле; — средняя длина свободного пробега фононов. Константа определяется свойствами вещества. Теплопроводность твердых тел во много раз превосходит теплопроводность газов.
Явления переноса Явления переноса в жидкостях Диффузия. Механизм диффузии в жидкостях аналогичен механизму диффузии в твердом теле. Молекула скачками меняет свое окружение и переходит в другую точку. Если среднее время «оседлой» жизни молекулы между скачками обозначить , то — среднее расстояние, на которое перескакивает молекула при изменении своего окружения. Время в жидкости также определяется через вероятность перескока. Энергия активации W молекулы, так же как и D0, определяется свойствами жидкости. Коэффициент диффузии у жидкостей много меньше, чем у газов, но много больше, чем у твердых тел (
Явления переноса Теплопроводность. Так же как и в тв. телах, теплопроводность в жидкостях осуществляется передачей теплового движения от одних молекул к другим в результате взаимодействия. Вязкость. Механизм возникновения вязкости в жидкостях не удается представить столь просто, как в разреженных газах, когда картина сводится к переносу импульса упорядоченного движения слоев газа при переходе молекул из одного слоя в другой в результате молекулярного движения. Если принять эту картину и применить механизм «скачков» молекулы из «оседлого» положения в одном слое в «оседлое» положение молекулы в другом слое, то для динамической вязкости получается противоречащая эксперименту зависимость от температуры, а именно в то время как эксперимент обнаруживает
Явления переноса «Перескоки» молекулы из одного «оседлого» положения в другое необходимо рассматривать в направлении действия силы, т.е. перпендикулярно градиенту скорости. При этом процесс оказывается зависящим от конкретных особенностей межмолеку- межмолекулярных сил. Молекуле приходится «вырываться» из своего окружения, чтобы передвинуться в направлении действия силы. Связи между молекулами, которые при этом приходится преодолевать, аналогичны тем, которые преодолеваются при испарении. Динамическая вязкость достаточно хорошо описывается формулой вида где А и b определяются свойствами жидкости. Следствие: при повышении температуры динамическая вязкость сильно уменьшается. Такое поведение динамической вязкости жидкостей противоположно наблюдаемому у газов.
Видео:Явления переноса Теплопроводность и вязкостьСкачать

Явление переноса. Общее уравнение переноса
1.3 Явление переноса. Общее уравнение переноса
Группа явлений, обусловленных хаотическим движением молекул и приводящих при этом к передаче массы, кинетической энергии и импульса, называется явлением переноса.
К ним относят диффузию – перенос вещества, теплопроводимость – перенос кинетической энергии и внутреннее трение – перенос импульса.
Общее уравнение переноса, описывающее эти явления, можно получить на основе молекулярно-кинетической теории.
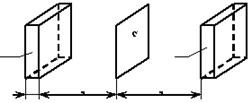
Пусть через площадку площадью «S» (рисунок) переносится некоторая физическая величина в результате хаотического движения молекул.
Похожие работы
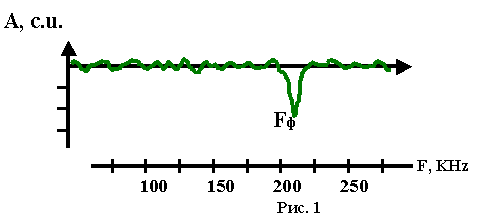
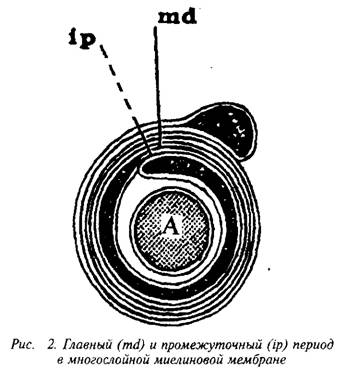
. материалы хорошо описываются в рамках квантово-механической фононной Модели строения и функционирования клеточных мембран, что позволяет утверждать: “ФОНОН – КВАНТ биологической (клеточной) мембраны”. Модель пригодна для объяснения широкого круга наблюдаемых явлений. При этом наблюдаемые явления описываются в рамках единого понятийного аппарата и не требуют специфических допущений для описания .
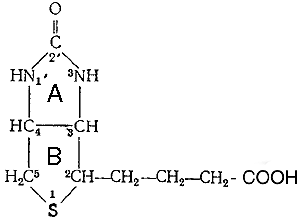
. активность тиамина и некоторых его производных. За последние 20 лет наряду выяснением механизма основных реакций, в которых каталитическую роль играет ТДФ, стали накапливаться данные о высокой биологической активности других некоферментных производных тиамина. Отчетливо наметились два направления исследований: возможное, участие различных фосфорных эфиров витамина в активном переносе .
. формами географической (территориально-механической) изоляции, известны и разные формы биологической изоляции, которые могут быть разбиты на три основные группы: эколого-этологическую, морфо-физиологическую и собственно генетическую. Биологическая изоляция приводит к уменьшению вероятности встречи особей разных полов в период размножения, снижению полового влечения и эффективности спаривания, к .
. и инозитолтрифосфат подвергаются химическим превращениям, требующим АТФ и ЦТФ и приводящим к восстановлению три-фосфоинозитида. Таким образом, цикл замыкается и уровень полифосфоинозитидов в мембране восстанавливается. 7. МИЕЛИН В ЦЕНТРАЛЬНОЙ НЕРВНОЙ СИСТЕМЕ Мозг человека содержит 120 г миелина, что составляет одну треть его сухой массы. Миелин – уникальное образование, организация которого .
Видео:Явления переноса. Диффузия.Скачать

Явления переноса. Диффузия, вязкость, теплопроводность. Коэффициенты диффузии, вязкости, теплопроводности.
Читайте также:
|


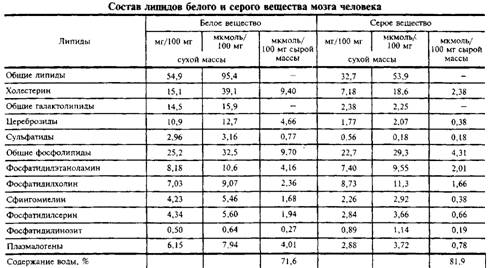
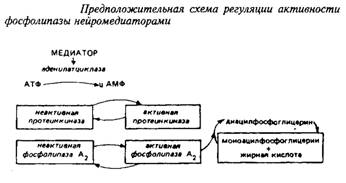
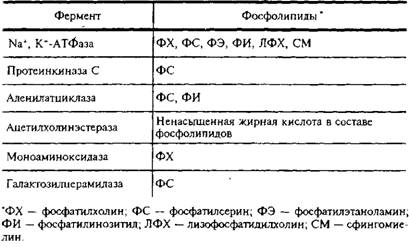
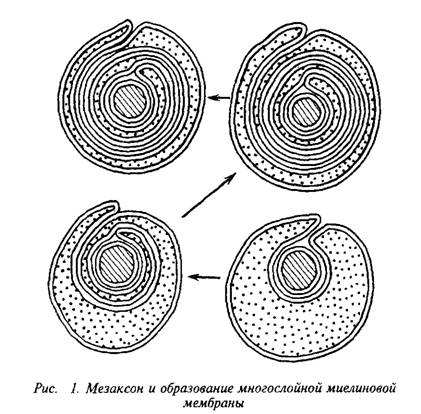
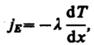 (48.1)
(48.1) 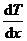 — градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры (поэтому знаки jE и
— градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры (поэтому знаки jE и 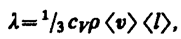 (48.2)
(48.2) 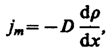 (48.3)
(48.3) 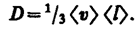 (48.4)
(48.4) 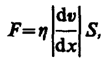 (48.5)
(48.5) 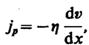 (48.6)
(48.6)  — градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости (поэтому знаки jр и
— градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости (поэтому знаки jр и 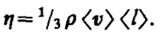 (48.7)
(48.7)