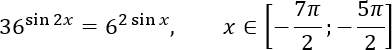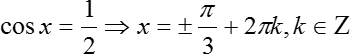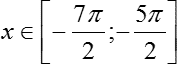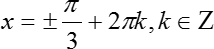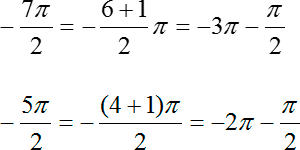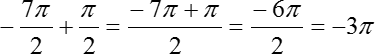Комбинированные уравнения с тригонометрическими функциями

Открытый банк заданий по теме показательно-тригонометрические уравнения. Задания C1 из ЕГЭ по математике (профильный уровень)

Видео:УРОК 4 4 КОМБИНИРОВАННЫЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ С ОГРАНИЧЕНИЯМИ.Скачать

Задание №1168

Условие

а) Решите уравнение 0,2^-26cdot 0,2^+25=0.

б) Укажите корни этого уравнения, принадлежащие отрезку left[ -pi ; frac2right].

Решение

а) Запишем уравнение в виде

5cdot 0,2^-26sqrt 5cdot 0,2^+25=0. После замены t=0,2^ исходное уравнение примет вид 5t^2-26sqrt 5t+25=0. Корни этого уравнения t=5sqrt 5, t=frac1. Возвращаясь к переменной x , получим:

Первое уравнение совокупности не имеет корней. Решая второе уравнение, получим:

x=pm fracpi 3+2pi n, n in mathbb Z.

б) Запишем решение уравнения в виде x=fracpi 3 +2pi k, k in mathbb Z или x=-fracpi 3+2pi n,nin mathbb Z и выясним, для каких целых значений n и k справедливы неравенства -pi leqslant -frac 3+2pi n leqslant frac2 и -pi leqslant fracpi 3+2pi kleqslant frac2.

Получим: -frac13leqslant nleqslant frac и -frac23leqslant kleqslant frac, откуда следует, что два целых значения n=0 и k=0 удовлетворяют соответствующим неравенствам.

При n=0enspace x=fracpi 3+2picdot 0=fracpi 3.

При k=0enspace x=-fracpi 3+2picdot 0=-fracpi 3.

Итак, fracpi 3 и -fracpi 3 — корни уравнения, принадлежащие промежутку left[ -pi ; frac2right].

Ответ

а) pmfracpi 3+2pi n, nin mathbb Z;

б) -fracpi 3, fracpi 3;

Видео:Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Комбинированные уравнения с тригонометрическими функциями

Видео:УРОК 4 5 КОМБИНИРОВАННЫЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ С ОГРАНИЧЕНИЯМИ.Скачать

Методы решения тригонометрических уравнений.

Видео:Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

1. Алгебраический метод.

( метод замены переменной и подстановки ).

Видео:Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

2. Разложение на множители.

П р и м е р 1. Решить уравнение: sin x + cos x = 1 .

Р е ш е н и е . Перенесём все члены уравнения влево:

sin x + cos x – 1 = 0 ,

преобразуем и разложим на множители выражение в

левой части уравнения:

П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.

Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,

sin x · cos x – sin 2 x = 0 ,

sin x · ( cos x – sin x ) = 0 ,

П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.

Р е ш е н и е . cos 2 x + cos 6 x = 1 + cos 8 x ,

2 cos 4x cos 2x = 2 cos ² 4x ,

cos 4x · ( cos 2x – cos 4x ) = 0 ,

cos 4x · 2 sin 3x · sin x = 0 ,

1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,

Видео:УРОК 3.4-КОМБИНИРОВАННЫЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ БЕЗ ОГРАНИЧЕНИЙСкачать

3. Приведение к однородному уравнению.

а) перенести все его члены в левую часть;

б) вынести все общие множители за скобки;

в) приравнять все множители и скобки нулю;

г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на

cos ( или sin ) в старшей степени;

д) решить полученное алгебраическое уравнение относительно tan .

П р и м е р . Решить уравнение: 3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.

Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,

sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,

tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,

корни этого уравнения: y ₁ = — 1, y ₂ = — 3, отсюда

1) tan x = –1, 2) tan x = –3,

Видео:Тригонометрические уравнения | Борис ТрушинСкачать

4. Переход к половинному углу.

П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7.

Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =

= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,

2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,

tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,

Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

5. Введение вспомогательного угла.

где a , b , c – коэффициенты; x – неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos и sin ( здесь — так называемый вспомогательный угол ), и наше уравнение прини мает вид:

Видео:Комбинированные тригонометрические уравненияСкачать

6. Преобразование произведения в сумму.

П р и м е р . Решить уравнение: 2 sin x · sin 3 x = cos 4 x .

Р е ш е н и е . Преобразуем левую часть в сумму:

Видео:Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать

Задача C1: тригонометрия и показательная функция — 2 вариант

17 февраля 2014

Сегодня мы разберем еще одну комбинированную задачу из части С ЕГЭ по математике, где требуется решить уравнение, содержащее в себе и показательную, и тригонометрическую функцию.

Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку:

Видео:СЕКРЕТНЫЙ ЛАЙФХАК С ТРИГОНОМЕТРИЕЙ НА ЕГЭ #shorts #математика #егэ #огэ #тригонометрияСкачать

Шаг 1: решение тригонометрического уравнения

Итак, нужно решить уравнение:

36 sin 2 x = 6 2sin x

Очевидно, перед нами комбинированная конструкция, содержащая в себе и показательное, и тригонометрическое уравнение.

Синус двойного угла

Как решать такое уравнение? Давайте для начала выпишем все тригонометрические функции, которые присутствуют в этом уравнении, а именно:

Что мы можем сказать о полученных выражениях? В первом (sin 2 x ) аргумент синуса — это 2х; а во втором (2sin x ) аргумент — просто x . Итак, аргументы наших тригонометрических функций не совпадают. Это первое, на что нужно обратить внимание при решении любого тригонометрического уравнения. Следовательно, каким-то образом нужно сделать так, чтобы аргументы стали одинаковыми. В данном случае все очень просто, ведь мы знаем формулу двойного угла:

sin 2 x = 2sin x · cos x;
36 2sin x cos x = 6 2sin x .

Решение показательного уравнения

Теперь у нас другая проблема: перед нами [показательное уравнение], в котором присутствуют функции с разными основаниями. Слева основание показательной степени 36, а справа — 6. И это еще один принципиальный момент: нам нужно сделать так, чтобы и слева, и справа основание показательной функции было одним и тем же. Для этого заметим, что 36 можно записать так:

Следовательно, мы можем переписать наше уравнение в следующем виде:

(6 2 ) 2sin x cos x = 6 2sin x

Теперь воспользуемся правилом возведения степени в степень: при возведении степень в степень, показатели этих степеней перемножаются. В нашем случае получаем:

( a 2 ) f ( x ) = a 2 f ( x ) ;
6 4sin x cos x = 6 2sin x .

Итак, мы получили классическое показательное уравнение, в котором основания степеней являются константами и равны друг другу. Следовательно, мы можем просто убрать их и записать:

4sin x cos x = 2sin x

Решение тригонометрического уравнения

Тригонометрическое уравнение, которое мы получили, содержит несколько элементов с тригонометрической функцией. Для решения такого уравнения предлагаю перенести все слагаемые в левую часть, в результате чего получим:

4sin x cos x − 2sin x = 0

В полученном уравнении присутствуют два алгебраических слагаемых, причем и в первом, и во втором имеется множитель 2sin x . Выносим 2sin x за скобку:

2sin x (2cos x − 1) = 0

Вынесение за скобку общего множителя

Обратите внимание: на этом шаге многие ученики допускают ошибку! Давайте я еще раз напомню, как выносить общий множитель за скобку. Для этого выпишем наше выражение еще раз:

4sin x cos x − 2sin x

Перепишем эту конструкцию следующим образом:

2 · 2sin x cos x − 2sin x

Отсюда нам нужно вынеси [общий множитель]. Как вообще определяется, что можно вынести множитель за скобку? Простым перебором: мы берем самое первое слагаемое в нашем выражении и рассматриваем самый первый множитель, входящий в это слагаемое. Таким множителем является число 2.

А теперь — вопрос: встречается ли множитель 2 во втором нашем слагаемом? Конечно, встречается! Значит, ее мы выносим и идем далее. Следующий множитель тоже 2, но второй двойки во втором слагаемом не имеется, поэтому еще одну двойку вынести за скобку мы не можем.

Идем дальше: множитель sin x . Присутствует ли sin x во втором слагаемом? Да, безусловно. И последний множитель из первого слагаемого — cos x . Есть ли он во втором слагаемом? Нет, такого множителя во втором слагаемом нет. Поэтому вынести за скобку множитель cos x мы не можем. Вот и все. Получается, что из нашей конструкции можно вынести за скобку лишь множители 2 и sin x .

2 · 2sin x cos x − 2sin x = 2sin x (2cos x − 1)

Но на этом проблемы не заканчиваются. Когда ученики записывают элементы в скобках, здесь часто допускаются совершенно нелепые ошибки. Поэтому всем своим ученикам я рассказываю одно и то же правило, которое [гарантировано] избавит вас от всех подобных проблем. Правило звучит следующим образом:

При вынесении за скобку общего множителя обязательно ставьте единицу на месте каждого вынесенного элемента!

Такая запись является гарантом того, что вы не допустите ошибку при вынесении множителя за скобку. Давайте посмотрим, как это правило сработает для нашего выражения. Записываем готовое разложение — и мы получили именно то выражение, которое у нас получилось в самом начале:

2 · 2sin x cos x − 2sin x = 2sin x (1 · 2 · 1cos x − 1 · 1) = 2sin x (2cos x − 1)

Решение простейших тригонометрических уравнений

С вынесением общего множителя за скобку разобрались, возвращаемся к нашему уравнению. Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю. Получаем несколько вариантов:

2 = 0; sin x = 0 (х = π n , n ∈ Z ); 2cos x − 1 = 0.

Очевидно, что уравнение 2 = 0 корней не имеет (Что за бред вообще?). Второе уравнение мы разобрали сразу, т.к. это был частный случай. Рассмотрим теперь последнее уравнение:

Уравнение решено. Мы разобрали каждый вариант, поэтому других корней не будет.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Отбор корней на отрезке

Переходим ко второй части задачи C1 — отбору корней в отрезке:

И снова предлагаю вашему вниманию небольшое усовершенствование.

Хитрость: отмечаем корни на тригонометрическом круге

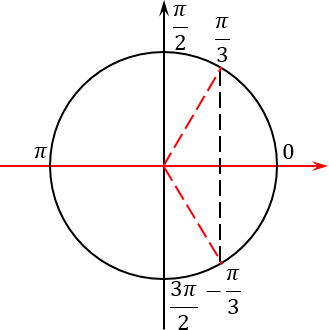
Этот прием я разработал совсем недавно вместе со своими учениками. Суть приема проста: чертим тригонометрический круг (в простонародье — радар) и отмечаем на нем наши корни. Сначала — первую группу:

Это одна точка в самом начале круга и еще одна точка, которая диаметрально противоположна исходной.

Теперь отмечаем вторую группу корней:

Поскольку период 2π k — это полный оборот окружности, никаких других точек на тригонометрическом круге точно не появится. Итого получим следующую картинку:

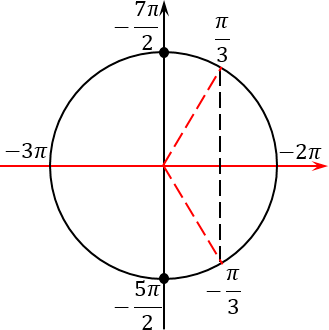
Все, корни мы отметили. Теперь разбираемся с концами отрезка. Давайте перепишем их в таком виде:

По существу, мы просто выделили целую часть — по аналогии с неправильными дробями в арифметике. Отметим эти точки на том же тригонометрическом круге:

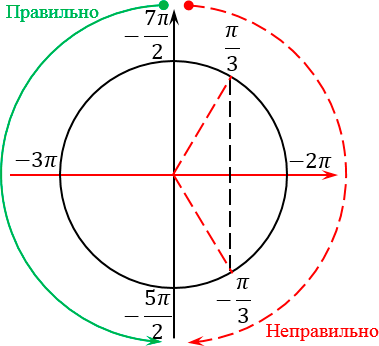
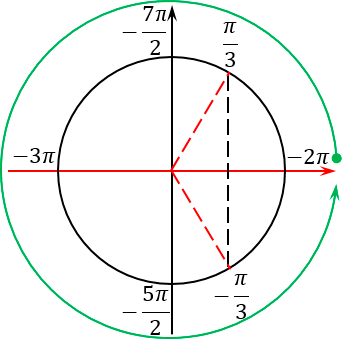
Отлично, концы искомого отрезка отмечены. Осталось грамотно отметить сам отрезок. Для этого нужно понять, как он расположен на нашем тригонометрическом круге. И вот тут многие ученики опять допускают ошибку: они путаются, в какую сторону «наматывать» этот отрезок. Ведь существует два варианта — против часовой стрелки (это правильный вариант) и по часовой (соответственно, неправильный):

На самом деле, чтобы никогда больше не путаться, нужно вспомнить основное правило: мы всегда накручиваем углы в сторону, противоположную движению часовой стрелки. Например, если бы мы хотели попасть из точки 0 в точку 2π, мы бы двигались именно против часовой стрелки:

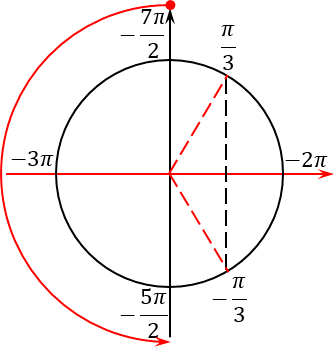
Это правило все прекрасно помнят, когда считают значение тригонометрических функций. Но почему-то забывают, что это правило работает для любых отрезков, а не только в пределах от 0 до 2π. Поэтому еще раз смотрим на наш исходный отрезок, берем его левый конец, т. е. самое маленькое число −7π/2, и идем от него в наш второй конец против часовой стрелки:

Прекрасно, отрезок отмечен. Для того, чтобы выявить интересующие нас корни, давайте продолжим лучи, проходящие через все корни, отмеченные красным, за пределы тригонометрического круга (по сути — до бесконечности). Таких лучей будет 4 штуки.

А теперь берем ручку, ставим ее в самый левый конец отрезка (точку −7π/2) и начинаем двигаться ко второму концу отрезка. Разумеется, мы тут же наткнемся на пересечение нашего отрезка и одного из лучей, отвечающих за корни. Так вот: любое такое пересечение означает, что мы нашли конкретный корень, который лежит на нашем рассматриваемом отрезке.

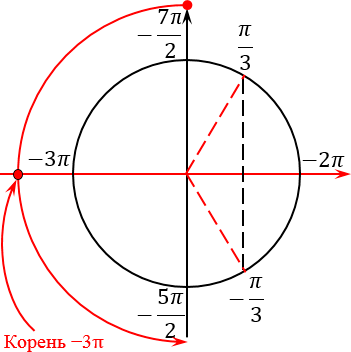
Возникает вопрос: как найти числовое значение этого корня? Но и тут все очень просто. Давайте подумаем: на какое расстояние нужно шагнуть из точки −7π/2, т. е. из начала нашего отрезка, чтобы попасть на горизонтальный диаметр? Очевидно, что это расстояние равно π/2. Прибавляем к концу нашего отрезка этот самый шаг:

В данном случае получилось, что этот корень уже изначально был отмечен, когда мы отмечали концы нашего отрезка: −7π/2 и −5π/2.

Если мы пойдем дальше, двигаясь из точки -3π к правому концу нашего отрезка, никаких других корней уже не встретим. Получается, что во время обхода мы столкнулись лишь с одним корнем — −3π. В принципе, это и неудивительно: в данной задаче нам попался довольно короткий отрезок, который на тригонометрическом круге занимает лишь половину полного оборота. И так уж получилось, что большинство корней, которые мы получили при решении уравнения, сосредоточены на второй половине нашего круга — в той самой, которую мы вообще не рассматривали.

В общем, не стоить удивляться, когда в процессе отбора корней у нас получился всего лишь один ответ. Это правильный ответ, и приведенный выше рисунок является полноценным тому обоснованием. Следовательно, задача решена полностью:

1. Мы решили само уравнение, последовательно разобравшись с показательным и тригонометрическим уравнением;
2. Затем отобрали те корни, которые лежат на требуемом отрезке, и обосновали этот выбор графически.

Видео:Арк-функции. Простейшие тригонометрические уравнения | Осторожно, спойлер! | Борис Трушин !Скачать

Замечание по поводу разложения на множители

Еще один тонкий момент в решении данной задачи состоит в том, что многие ученики неправильно выносят за скобку общие множители. Но это — тема отдельного урока, который вообще не относится к ЕГЭ по математике, поэтому сегодня я коснулся данного вопроса лишь вкратце. Ровно настолько, насколько это необходимо для решения конкретной задачи.

Однако если в сегодняшнем уроке вам все равно что-то непонятно, если вы хотите решать тригонометрию еще лучше, не нужно расстраиваться, просто заходите на мой сайт berdov . com . Там вас ждет еще больше уроков, а также тесты для самостоятельного решения.

Но и это еще не все: на любой странице моего сайта справа вверху есть форма для записи на занятие. Смело заполняйте ее, указывайте свое имя, телефон и хоть немного расскажите о своей математической проблеме. И как только вы нажмете на кнопку «Записаться», буквально через несколько секунд я получу ваше сообщение, и в течение нескольких минут (максимум — нескольких часов) я вам позвоню, и мы обсудим все интересующие проблемы и составим индивидуальную программу обучения, рассчитанную именно на вас.

И вот тогда вы точно убедитесь, что математика — это, на самом деле, легко, что никаких сложных формул и теорем в ней нет. Тем более, в школьном курсе. Пишите, звоните, приходите — и будем заниматься. А у меня на сегодня все. С Вами был Павел Бердов. До новых встреч!

📺 Видео

Простейшие тригонометрические уравнения. y=cosx. 1 часть. 10 класс.Скачать

10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Подготовка к ЕГЭ #95. Решение уравнений, содержащих обратные тригонометрические функцииСкачать

УРОК 3.5 РЕШЕНИЕ КОМБИНИРОВАННЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ БЕЗ ОГРАНИЧЕНИЙСкачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

Обратные тригонометрические функции #1Скачать

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 11 класс графики тригонометрических функцийСкачать