В математических описаниях часто фигурирует термин «числовой коэффициент», например, в работе с буквенными выражениями и выражениями с переменными. Материал статьи ниже раскрывает понятие этого термина, в том числе, на примере решения задач на нахождение числового коэффициента.
- Определение числового коэффициента. Примеры
- Нахождение числового коэффициента выражения
- График линейной функции, его свойства и формулы
- Понятие функции
- Понятие линейной функции
- Свойства линейной функции
- Построение линейной функции
- Решение задач на линейную функцию
- Метод неопределенных коэффициентов и его универсальность
- 🎬 Видео
Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Определение числового коэффициента. Примеры
Учебник Н.Я. Виленкина (учебный материал для учащихся 6 классов) задает такое определение числового коэффициента выражения:
Если буквенное выражение является произведением одной или нескольких букв и одного числа, то это число называется числовым коэффициентом выражения.
Числовой коэффициент зачастую называют просто коэффициентом.
Данное определение дает возможность указать примеры числовых коэффициентов выражений.
Рассмотрим произведение числа 5 и буквы a , которое будет иметь следующий вид: 5 · a . Число 5 является числовым коэффициентом выражения согласно определению выше.
В заданном произведении x · y · 1 , 3 · x · x · z десятичная дробь 1 , 3 – единственным числовой множитель, который и будет служить числовым коэффициентом выражения.
Также разберем такое выражение:
7 · x + y . Число 7 в данном случае не служит числовым коэффициентом выражения, поскольку заданное выражение не является произведением. Но при этом число 7 – числовой коэффициент первого слагаемого в заданном выражении.
Пусть дано произведение 2 · a · 6 · b · 9 · c .
Мы видим, что запись выражения содержит три числа, и, чтобы найти числовой коэффициент исходного выражения, его следует переписать в виде выражения с единственным числовым множителем. Собственно, это и является процессом нахождения числового коэффициента.
Отметим, что произведения одинаковых букв могут быть представлены как степени с натуральным показателем, поэтому определение числового коэффициента верно и для выражений со степенями.
Выражение 3 · x 3 · y · z 2 – по сути оптимизированная версия выражения 3 · x · x · x · y · z · z , где коэффициент выражения – число 3 .
Отдельно поговорим о числовых коэффициентах 1 и — 1 . Они очень редко записаны в явном виде, и в этом их особенность. Когда произведение состоит из нескольких букв (без явного числового множителя), и перед ним обозначен знак плюс или вовсе нет никакого знака, мы можем говорить, что числовым коэффициентом такого выражения является число 1 . Когда перед произведением букв обозначен знак минус, можно утверждать, что в этом случае числовой коэффициент – число — 1 .
Далее определение числового коэффициента расширяется с произведения нескольких букв и числа до произведения числа и нескольких буквенных выражений.
К примеру, в произведении — 5 · x + 1 число — 5 будет служить числовым коэффициентом.
По аналогии, в выражении 8 · 1 + 1 x · x число 8 – коэффициент выражения; а в выражении π + 1 4 · sin x + π 6 · cos — π 3 + 2 · x числовой коэффициент — π + 1 4 .
Видео:Метод неопределенных коэффициентов. 10 класс.Скачать

Нахождение числового коэффициента выражения
Выше мы говорили о том, что если выражение представляет собой произведение с единственным числовым множителем, то этот множитель и будет являться числовым коэффициентом выражения. В случае, когда выражение записано в ином виде, предстоит совершить ряд тождественных преобразований, который приведет заданное выражение к виду произведения с единственным числовым множителем.
Задано выражение − 3 · x · ( − 6 ) . Необходимо определить его числовой коэффициент.
Решение
Осуществим тождественное преобразование, а именно произведем группировку множителей, являющихся числами, и перемножим их. Тогда получим: − 3 · x · ( − 6 ) = ( ( − 3 ) · ( − 6 ) ) · x = 18 · x .
В полученном выражении мы видим явный числовой коэффициент, равный 18 .
Ответ: 18
Задано выражение a — 1 2 · 2 · a — 6 — 2 · a 2 — 3 · a — 3 . Необходимо определить его числовой коэффициент.
Решение
С целью определения числового коэффициента преобразуем в многочлен заданное целое выражение. Раскроем скобки и приведем подобные слагаемые, получим:
a — 1 2 · 2 · a — 6 — 2 · a 2 — 3 · a — 3 = = 2 · a 2 — 6 · a — a + 3 — 2 · a 2 + 6 · a — 3 = — a
Числовым коэффициентом полученного выражения будет являться число — 1 .
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

График линейной функции, его свойства и формулы
О чем эта статья:
Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Понятие функции
| Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. |
|---|
Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:
Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.
Графический способ — наглядно. Его мы и разберем в этой статье.
| График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу. |
|---|
Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Понятие линейной функции
| Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент. |
|---|
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Нам дана функция: у = 0,5х — 2. Значит:
если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0 и т. д.
Для удобства результаты можно оформлять в виде таблицы:
| х | 0 | 2 | 4 |
| y | -2 | -1 | 0 |
Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.
| Функция | Коэффициент k | Коэффициент b |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.
Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Свойства линейной функции
Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит, y = b — четная;
b = 0, k ≠ 0, значит, y = kx — нечетная;
b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;
b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (−b/k; 0);
ось ординат OY — в точке (0; b).
x = −b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).
При k 0, то этот угол острый, если k
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
если k > 0, то график наклонен вправо;
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Если k > 0 и b
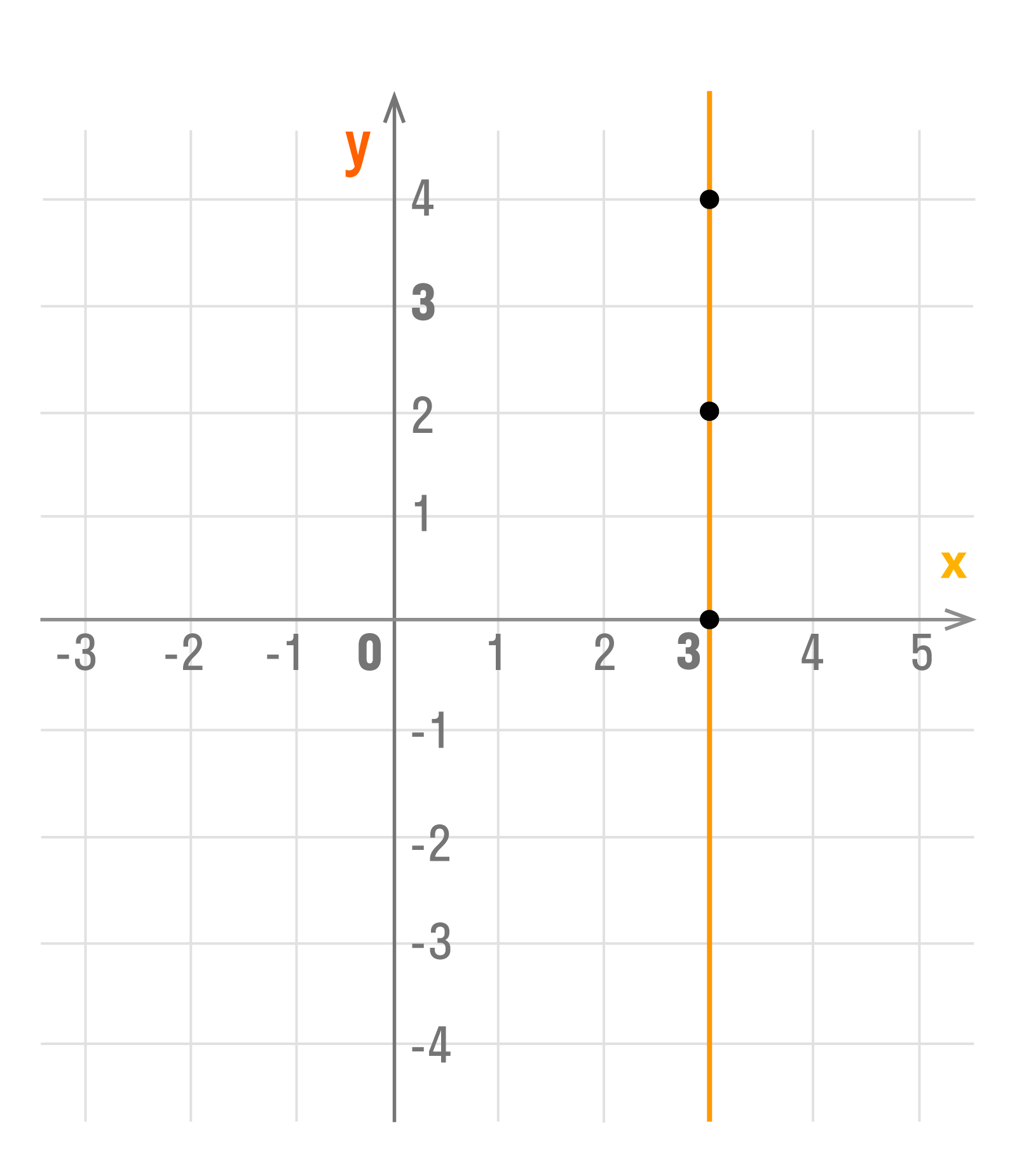
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Ответ: уравнение прямой y = 3x — 2.
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Метод неопределенных коэффициентов и его универсальность
Разделы: Математика
Применение метода неопределённых коэффициентов основано на следующих двух теоремах.
Теорема №1 (о многочлене, тождественно равном нулю).
Если при произвольных значениях аргумента x значение многочлена f(x) = а0+ а1х + а2х 2 +. + а nx n , заданного в стандартном виде, равно нулю, то все его коэффициенты а0, а1, а2, . аn равны нулю.
Теорема №2 (следствие теоремы № 1).
Деление многочлена на многочлен.
Пример 1. Выполнить деление многочлена х 5 – 6х 3 + 2х 2 -4 на многочлен х 2 – х + 1.
Решение: Надо найти такие многочлены Q(x) и R(x), что х 5 – 6х 3 + 2х 2 -4 = (х 2 – х + 1) Q(x) + R(x), причём степень многочлена R(x) меньше степени многочлена (х 2 – х + 1). Из того, что степень произведения многочленов равна сумме их степеней, следует, что степень многочлена Q(x) равна 5 – 2 = 3.
Многочлены Q(x) и R(x) имеют вид:
Раскроем скобки в правой части равенства:
Для отыскания неизвестных коэффициентов получаем систему уравнений:
Ответ: Q(x) = x 3 + x 2 — 6x — 5, R(x) = x + 1.
Пример 2. Выполнить деление многочлена х 7 –1 на многочлен х 3 + х + 1.
Решение: Надо найти такие многочлены Q(x) и R(x), что х 7 –1 = (х 3 + х + 1) Q(x) + R(x), причём степень многочлена R(x) меньше степени многочлена (х 3 + х + 1).
Из того, что степень произведения многочленов равна сумме их степеней, следует, что степень многочлена Q(x) равна 7– 3 = 4.
Многочлены Q(x) и R(x) имеют вид: Q(x) = q 4x 4 + q 3x 3 + q 2x 2 + q 1x + q0,
R(x) = r 2x 2 + r 1x + r0.
Подставим Q(x) и R(x):
Раскроем скобки в правой части равенства:
Получаем систему уравнений:
Ответ: Q(x) = x 4 — x 2 — x + 1, R(x) = 2x 2 — 2.
Расположение многочлена по степеням.
Возьмем функцию 
Задача сводится к нахождению неизвестных коэффициентов а0, а1, . аn. В каждом конкретном случае эти числа найти легко. Действительно, расположим многочлены, находящиеся в левой и правой частях равенства, по степеням x. Так как мы имеем тождество, то (по теореме № 2) коэффициенты при одинаковых степенях x должны быть равны между собой. Приравняв коэффициенты правой части соответствующим заданным коэффициентам левой, мы придем к системе n+1 уравнений с n+1 неизвестными а0, а1, . аn , которую нужно решить.
Пример 3. Расположим многочлен 

Приравниваем коэффициенты при одинаковых степенях и получаем систему:
Решая систему, находим:
Ответ: 
Пример 4. Расположим f(x) = х 4 — 8х 3 + 24х 2 — 50х + 90 по степеням (х-2).
Решение: Полагаем х4 — 8х 3 + 24х 2 — 50х + 90
Ответ: f(x) =
Представление произведения в виде многочлена стандартного вида.
Пример 5. Не выполняя действий, представим в виде многочлена стандартного вида произведение (х — 1)(х + 3)(х + 5).
Решение: Произведение есть многочлен третьей степени, коэффициент при старшем члене равен 1, а свободный член равен (- 15), тогда запишем:
(х — 1)(х + 3)(х + 5) = х 3 + ах 2 + вх — 15, где а и в — неизвестные коэффициенты.
Для вычисления их положим х = 1 и х = — 3, тогда получим:

Ответ: х 3 +7х 2 + 7х — 15.
Разложение многочлена на множители
Пример 6. Дан многочлен
Разложим его на множители, если известно, сто все его корни – целые числа.
Решение: Будем искать разложение в виде:
полагая числа a, b, c и d его корнями. Раскроем скобки в правой части и сгруппируем по одинаковым степеням.
Приравниваем коэффициенты при одинаковых степенях.
Так как корни нашего многочлена – целые, то из последнего уравнения системы заключаем, что они должны быть делителями числа 30. Следовательно, их следует искать среди чисел
Проведя испытания, установим, что корни нашего многочлена -2, -5, 1 и 3. Следовательно х 4 + 3х 3 — 15х 2 — 19х + 30 = (х — 1)(х — 3)(х + 2)(х + 5)
Пример 7. Дан многочлен 
Разложим его на множители, если известно, сто все его корни – целые числа.
Решение: Будем искать разложение в виде:
полагая числа a, b, c и d его корнями. Раскроем скобки в правой части и сгруппируем по одинаковым степеням.
Приравниваем коэффициенты при одинаковых степенях.
Так как корни нашего многочлена – целые, то из последнего уравнения системы заключаем, что они должны быть делителями числа 84. Следовательно, их следует искать среди чисел
Проведя испытания, установим, что корни нашего многочлена -7,-2,2,3. Следовательно х 4 + 4х 3 — 25х 2 — 16х + 84 = (х — 2)(х — 3)(х + 2)(х + 7)
Пример 8. Разность 
Решение: Так как,
Тогда
Положим 
Тогда
Решая данную систему уравнений, получим а = 5, b = -4.
Значит 
Аналогично устанавливаем, что
Следовательно
Пример 9. Является ли разность 
Решение: Т.к.
тогда —
Положим 
Тогда 
из второго уравнения 
b 2 = 12,5 — — не удовлетворяет условию задачи, или b 2 = 9, откуда b = -3 или b = 3 — не удовлетворяет числу 
Аналогично,
Окончательно получаем: 
Уничтожение иррациональности в знаменателе
Пример 10. Избавимся от иррациональности в знаменателе:
Решение:
отсюда
Раскроем скобки, сгруппируем:
Ответ:
Пример 11. Избавимся от иррациональности в знаменателе:
Решение: 
отсюда
Раскроем скобки, сгруппируем
Отсюда
Итак
Следовательно
Ответ:
Применение метода неопределенных коэффициентов при решении уравнений
Пример 12. Решим уравнение х 4 + х 3 — 4х 2 — 9х — 3 = 0.
Решение: Предположим, что корни уравнения — целые числа, тогда их надо искать среди чисел
Если х = 1, то 
если х = -1, то 
если х = 3, то 
если х = -3, то
Отсюда делаем вывод, что рациональных корней наше уравнение не имеет.
Попробуем разложить многочлен 

Приравнивая соответствующие коэффициенты выражений для неизвестных a, b, c и d получаем систему уравнений:
Так как bd = -3, то будем искать решения среди вариантов:
Проверим вариант № 2, когда b = —1; d = 3:
Пример 13. Решить уравнение: х 4 — 15х 2 + 12х + 5= 0.
Решение: Разложим многочлен f(х) = х 4 — 15х 2 + 12х + 5 на множители в следующем виде: 
Приравнивая соответствующие коэффициенты выражений для неизвестных a, b, c и d получаем систему уравнений:
Так как , bd = 5, то будем искать решения среди вариантов:
Системе удовлетворяет вариант №2, т.е. а = 3, b = -1, c = -3, d = 5.
Итак,

D =13
D = 29
Ответ:
О решении одного класса кубических уравнений.
Пусть дано кубическое уравнение: а 1 х 3 + b 1х 2 +с 1х +d1 = 0, где а ≠ 0.
Приведём его к виду х 3 + ах 2 +bх + с = 0 (1), где а = 


Положим в уравнении (1) х = у + m. Тогда получим уравнение: 
Раскроем скобки, сгруппируем: y 3 +3у 2 m + 3ym 2 + m 3 + ay 2 + 2aym +am 2 + by +bm + с = 0,
y 3 + y 2 (a +3m) +y(3m 2 +2am +b) + m 3 +am 2 +bm + с = 0.
Для того, чтобы уравнение (1) было двучленным, должно выполняться условие:
Решения этой системы: m = —

Пример14. Решить уравнение: х 3 + 3х 2 +3х — 9 =0.
Решение: В данном уравнении а = 3, в =3, тогда условие a 2 = 3b выполняется, а m = — 
Уравнение принимает вид: (у -1) 3 +3(у -1) 2 +3(у -1) – 9 = 0.
y 3 -3y 2 +3у -1 +3у 2 – 6у +3 +3у –3 – 9 = 0.
y 3 – 10 = 0, откуда у = 

Ответ: 
Пример15. Решить уравнение: х 3 + 6х 2 + 12х + 5 = 0.
Решение: а = 6, в =12, тогда условие a 2 = 3b (62 = 3×12) выполняется, а m = — 
Выполним подстановку х = у — 2. Уравнение принимает вид: (у -2) 3 +6(у -2) 2 +12(у -2) + 5 = 0.
у 3 – 6у 2 + 12у – 8 + 6у 2 -24у + 24 + 12у – 24 + 5 = 0.
у 3 – 3 = 0, у = 

Ответ: 
Рассмотренные в работе примеры могут быть решены и другими способами. Но цель работы заключалась в том, чтобы решить их методом неопределённых коэффициентов, показать универсальность этого метода, его оригинальность и рациональность, не отрицая того, что в некоторых случаях он приводит к громоздким, но не сложным преобразованиям.
🎬 Видео
Уравнение прямой. Как построить график линейной функции. Коэффициент k и m.Скачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Расстановка Коэффициентов в Химических Реакциях // Подготовка к ЕГЭ по ХимииСкачать

Метод неопределенных коэффициентовСкачать

Как написать уравнения касательной и нормали | МатематикаСкачать

СУММА КОЭФФИЦИЕНТОВ: Как решать Квадратные Уравнения по МАТЕМАТИКЕ 8 классСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Занятие 1. График линейной функции y=kx+bСкачать