- Парабола, её форма, фокус и директриса.
- Свойства параболы.
- Уравнение касательной к параболе.
- Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
- Касательная к графикам функции в точке
- Основные значения угла наклона прямой
- Значение производной функции в точке и ее геометрический смысл
- Понятие уравнения касательной прямой
- Уравнение касательной
- Геометрический смысл производной в точке и касательной
- Готовые работы на аналогичную тему
- Уравнение касательной через производную
- Уравнение касательной для параболы
- Расположение касательной в зависимости от значения её углового коэффициента
- 📹 Видео
Видео:Касательная к параболеСкачать

Парабола, её форма, фокус и директриса.
Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
y^=2pxlabel
$$
при условии (p > 0).
Из уравнения eqref вытекает, что для всех точек параболы (x geq 0). Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.
Форма параболы известна из курса средней школы, где она встречается в качестве графика функции (y=ax^). Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством (2p=a^).
Фокусом параболы называется точка (F) с координатами ((p/2, 0)) в канонической системе координат.
Директрисой параболы называется прямая с уравнением (x=-p/2) в канонической системе координат ((PQ) на рис. 8.11).
Рис. 8.11. Парабола.
Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Свойства параболы.
Расстояние от точки (M(x, y)), лежащей на параболе, до фокуса равно
$$
r=x+frac
.label
$$
Вычислим квадрат расстояния от точки (M(x, y)) до фокуса по координатам этих точек: (r^=(x-p/2)^+y^) и подставим сюда (y^) из канонического уравнения параболы. Мы получаем
$$
r^=left(x-frac
right)^+2px=left(x+frac
right)^.nonumber
$$
Отсюда в силу (x geq 0) следует равенство eqref.
Заметим, что расстояние от точки (M) до директрисы также равно
$$
d=x+frac
.nonumber
$$
Следовательно, мы можем сделать следующий вывод.
Для того чтобы точка (M) лежала на параболе, необходимо и достаточно, чтобы она была одинаково удалена от фокуса и от директрисы этой параболы.
Докажем достаточность. Пусть точка (M(x, y)) одинаково удалена от фокуса и от директрисы параболы:
$$
sqrt<left(x-frac
right)^+y^>=x+frac
.nonumber
$$
Возводя это уравнение в квадрат и приводя в нем подобные члены, мы получаем из него уравнение параболы eqref. Это заканчивает доказательство.
Параболе приписывается эксцентриситет (varepsilon=1). В силу этого соглашения формула
$$
frac=varepsilonnonumber
$$
верна и для эллипса, и для гиперболы, и для параболы.
Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Уравнение касательной к параболе.
Выведем уравнение касательной к параболе в точке (M_(x_, y_)), лежащей на ней. Пусть (y_ neq 0). Через точку (M_) проходит график функции (y=f(x)), целиком лежащий на параболе. (Это (y=sqrt) или же (y=-sqrt), смотря по знаку (y_).) Для функции (f(x)) выполнено тождество ((f(x))^=2px), дифференцируя которое имеем (2f(x)f'(x)=2p). Подставляя (x=x_) и (f(x_)=y_), находим (f'(x_)=p/y_) Теперь мы можем написать уравнение касательной к параболе
$$
y-y_=frac
<y_>(x-x_).nonumber
$$
Упростим его. Для этого раскроем скобки и вспомним, что (y_^=2px_). Теперь уравнение касательной принимает окончательный вид
$$
yy_=p(x+x_).label
$$
Заметим, что для вершины параболы, которую мы исключили, положив (y_ neq 0), уравнение eqref превращается в уравнение (x=0), то есть в уравнение касательной в вершине. Поэтому уравнение eqref справедливо для любой точки на параболе.
Касательная к параболе в точке (M_) есть биссектриса угла, смежного с углом между отрезком, который соединяет (M_) с фокусом, и лучом., выходящим из этой точки в направлении оси параболы (рис. 8.12).
Рассмотрим касательную в точке (M_(x_, y_)). Из уравнения eqref получаем ее направляющий вектор (boldsymbol(y_, p)). Значит, ((boldsymbol, boldsymbol_)=y_) и (cos varphi_=y_/boldsymbol). Вектор (overrightarrow<FM_>) имеет компоненты (x_=p/2) и (y_), а потому
$$
(overrightarrow<FM_>, boldsymbol)=x_y_-frac
y_+py_=y_(x_+frac
).nonumber
$$
Но (|overrightarrow<FM_>|=x_+p/2). Следовательно, (cos varphi_=y_/|boldsymbol|). Утверждение доказано.
Заметим, что (|FN|=|FM_|) (см. рис. 8.12).
Видео:Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Время чтения: 30 минут
Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

Касательная к графикам функции в точке
Угол наклона прямой линии [y=k x+b] — это угол [a], который берет свой отсчет от положительного направления оси координат ox по направлению к прямой. Угол наклона может иметь значение как со знаком плюс, так и со знаком минус.
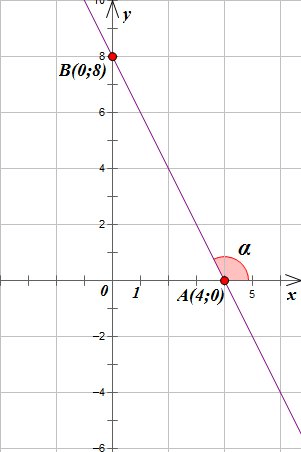
На расположенном рис.1 показана прямая и угол наклона относительно оси.
Для каждого угла наклона характерен угловой коэффициент прямой.
Угловой коэффициент — это числовой коэффициент прямой вида [boldsymbol]. В уравнение он обозначается буквой k.
Угловой коэффициент равен значению тангенса наклона заданной прямой линии: [k=operatorname alpha].
Видео:Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.Скачать

Основные значения угла наклона прямой
- Угол наклона прямой линии будет иметь нулевое значение, только в случае, когда параллельна ось Ox, и значение углового коэффициента равняется нулю. Потому что [operatorname 0=0]. Следовательно уравнение прямой будет записываться следующим образом: [y=b].
- В случае, когда угол наклона будет острым, то должно выполняться два следующих условия: [0 0]. При этом будет наблюдаться возрастание графика функции на протяжении всей координатной прямой.
- При условии, что угол [alpha=frac], из этого следует, что прямая будет располагаться относительно оси Ox в перпендикулярном положении. Условие задается следующим равенством [x=c]. Где с — это простое действительное число.
- Если угол наклона прямой, является тупым, то будет применяться следующее условие: [frac
Рисунок 2. Секущая прямая на графике функции.
На графике показана секущая, которая обозначена красным цветом и точками А и В.
Если угловой коэффициент прямой линии равен тангенсу угла наклона, то используя прямоугольный треугольник можно найти значение тангенса. Сделать это можно вычислением по правилу: тангенс равен отношению противолежащего катета к прилежащему.
Чтобы определить значение секущий, нужно использовать следующую формулу:
Значение секущий определяется, используя следующее неравенство:
Уравнение записывается следующим образом:
Касательная к графику функции — это прямая, которая проходит через определенную заданную точку, которая в свою очередь имеет отрезок с множеством числовых значений x.
Пример:
Прямая задана следующей функцией: [y=x+1]. Данная функция считается касательной к графику [y=2 sqrt] с координатными точками (1;2).
Рассмотрим графики со значениями (1;2). Функция обозначается черным цветом, а касательная линия соответственно синим цветом.
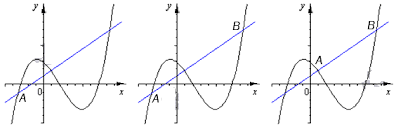
Чтобы определить касательную к функции, нужно исследовать поведение касательной АВ. При этом должно быть бесконечное приближение точки В к точке А.
Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Значение производной функции в точке и ее геометрический смысл
Для заданной функции [f(chi)] рассмотрим секущую АВ. Точки А и В заданы следующими значениями: [left(chi_, fleft(chi_right)right)] и [left(chi_+Delta chi ,left(chi_+Delta chiright)right.].
[Delta chi] — это показатель приращения значения аргумента.
Подставив все значения в исходную функцию получим следующий вид:
[Delta y=Delta f(chi)=fleft(chi_+Delta chiright)-f(Delta chi)].
Для более лучшего восприятия решения, построим график.
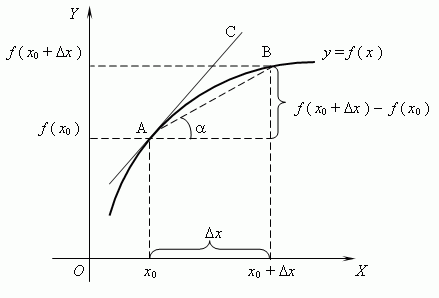
Из графика видно, что образуется прямоугольный треугольник ABC. Составим соотношение [frac=operatorname alpha], для этого необходимо применить основное определение тригонометрической функции, а именно тангенса.
Исходя из основного определения касательной, запишем следующее выражение:
Используя правило производной, имеем следующее:
- производная [f(x)] в точке [x_] — является пределом отношения приращения функции к аргументу.
- [Delta_ rightarrow 0 text fleft(x_right)=lim _ frac].
[k_] — это угловой коэффициент касательной функции.
Из данной функции можно сделать следующий вывод:
- функция [f(x)] может находится в точке со значением [x_]
- функция может быть касательной к графику в некой точке касания, где угловой коэффициент равняется производной.
Видео:Касательная к графику функции в точке. 10 класс.Скачать

Понятие уравнения касательной прямой
Чтобы составить уравнение прямой, нужно знать угловой коэффициент с заданной точкой. Это точка, через которую проходит прямая. При пересечении угловой коэффициент записывается как значение [x_].
Уравнение касательной записывается следующим образом:
График функции [y=f(x)].
Расположение касательной прямой непосредственно зависит от значения углового коэффициента. Если прямая параллельна оси Ox, то значение коэффициента равно нулевому значению. При параллельном расположении относительно оси Oy, коэффициент угловой принимает значение бесконечности. При это уравнение касательной записывается как: [x=x_].Также угловой коэффициент будет возрастать при значении больше нуля, а если коэффициент меньше нуля, то функция соответственно будет убывать.
Нужно составить уравнение касательной к графику функции.
Порядок решения: Из условия задачи следует, что функция может быть определенной для всех действительных значений. Точка, которая задана с координатами (1;3) будет являться точкой касания, следовательно , [x_=-1, fleft(x_right)=-3].
Для точки со значение равным -1, нужно определить производную. Для этого составим уравнение:
Показатель [f^(x)] в точке, которая является касательной, будет равен угловому коэффициенту.
Угловой коэффициент равен наклону тангенса. Отсюда следует, что:
Подведем итоги, и запишем ответ:
По условию задачи нужно определить касательную к графику функции [y=3 cdot sqrt[5]+1]. Точки координат равны (1;1). Также нужно составить уравнение и определить значение угла наклона. Согласно условию задачи, область определения функции — это простые действительные числа. Определим значение производной.
При условии, что [x_=1] тогда функция будет не определенной, но пределы ее можно записать как:
Это значит, что вертикальная касательная в точке существует.
Ответ: после всех проведенных вычислений уравнение приобретает вид x=1, где угол наклона будет равен [frac].
Видео:Уравнение касательнойСкачать

Уравнение касательной
Вы будете перенаправлены на Автор24
Вспомним определение секущей для лучшего понимания что такое касательная.
Секущей называют прямую, пересекающую график кривой в двух точках одновременно.
Касательной прямой к графику кривой называют прямую, проходящую через некую точку кривой и совпадающую с ней в этой точке так, что это прямая лишь касается кривой.
Другое и более ёмкое определение касательной дал Лейбниц.
Лейбниц касательной называл прямую, проведённую через пару точек на рассматриваемой кривой, не совпадающих между собой, но находящихся бесконечно близко друг к другу. Из определения Лейбница видно, что касательная является частным случаем секущей.
Видео:Прямая y=8x+11 параллельна касательной к графику функции y=x^2+7x-7. Найдите абсциссу точки касания.Скачать

Геометрический смысл производной в точке и касательной
Рассмотрим определение касательной подробнее.
Рисунок 1. Касательная и секущая к графику. Автор24 — интернет-биржа студенческих работ
Пусть дана некая кривая $L$, а на ней выбрана произвольная точка $M$. Возьмём ещё одну точку $P$, расположенную также на этой кривой и проведём через точки $M$ и $P$ секущую. Теперь поставим точку $P$ ещё ближе к точке $M$ и проведём новую секущую.
Проделаем так ещё несколько раз, каждый раз получая новую секущую, как бы поворачивающуюся вокруг точки $M$.
В момент, когда очередная точка $P$ находится бесконечно близко к точке $M$, секущая как бы достигает своего предельного положения, в котором по сути она лишь касается графика.
Готовые работы на аналогичную тему
Это положение называется касательной к графику кривой $L$ в точке $M$.
Видео:ЕГЭ Задание 7 Уравнение касательнойСкачать

Уравнение касательной через производную
Теперь узнаем, как найти уравнение касательной.
Рассмотрим некую функцию $y(x)$ и выберем на ней точку $M$ с координатами $(a; y(a))$.
Сделаем приращение к аргументу $x$ в этой точке, равное $Δx$ и рассмотрим точку $P$ на графике функции с абсциссой, равной $x=x+Δx$. Значение функции в этой точке будет равно $y(a+ Δx)$. Проведём через точки $M$ и $P$ секущую.
Как мы помним из курса математики, угловой коэффициент равен тангенсу угла прямой с осью абсцисс. Это значит, что угловой коэффициент рассматриваемой нами секущей равен приращению функции $y$ к приращению функции $x$:
Теперь рассмотрим приращение $Δx$ как бесконечно малую величину. В этом случае точка $P$ с координатами $(a; y(a)+ Δy)$ будет приближаться к точке $M$, стремясь к ней. Следовательно, угловой коэффициент нашей секущей, которая в данном случае является касательной, равен пределу:
Воспользуемся формулой $(1)$ для секущей:
Данный предел также носит название производной функции $y=f(x)$ в точке $x$ и обозначается как $y’(x)$.
Геометрический смысл производной состоит в том, что при условии возможности проведения касательной в точке $x$ к графику исследуемой кривой, такой, что эта касательная не параллельна оси $OX$, значение производной является угловым коэффициентом проведённой касательной в этой точке.
Иначе данное утверждение можно записать как
То есть, при составлении уравнения касательной через производную, производная функции является угловым коэффициентом.
Заметим на всякий случай, что сама функция $y=f(x)$ и её производная $y’(x)$ — две разные функции, равные между собой в точке $x$.
Таким образом, в общем виде уравнение касательной будет иметь вид:
где $f(x_0)$ — значение функции в точке $x_0$, а $f’(x_0)$ — её производная.
Видео:ЕГЭ по математике. Касательная к параболеСкачать

Уравнение касательной для параболы
Рисунок 2. Уравнение касательной к графику параболической функции. Автор24 — интернет-биржа студенческих работ
Рассмотрим получение уравнения касательной к графику функции на параболе $y=ax^2$ в точке $M$ c координатами $(x; y)$.
Придадим этой точке приращение по оси $OX$, равное $Δx$, приращение по оси $y$ тогда составит $y+Δy=a(x+ Δx)^2$. Точку с координатами $(x+ Δx; y+Δy)$ назовём $P$.
Теперь чтобы определить тангенс угла секущей $MP$с осью абсцисс, рассмотрим прямоугольный треугольник $triangle MNP$. В нём катет $MN$ равен $Δx$, а второй катет $Δy$ — это приращение ординаты, равное $Δy=a(2x cdot Δx + Δx^2)$.
Выразим используя эти данные тангенс угла $φ$.
$mathrmφ=frac=2ax + a cdot Δx$
Теперь для получения углового коэффициента рассмотрим это отношение при бесконечно малой величине $Δx$. Как известно, в этом случае мы имеем дело с пределом:
Благодаря такому соотношению становится легко построить касательную к параболе (рис. 2, б).
Для этого достаточно рассмотреть треугольник $triangle MPT$, так как отрезок $TP$ будет равен:
То есть, для того чтобы получить касательную, необходимо соединить середину отрезка $OP$ с точкой $M$.
Видео:14.1. Касательная к параметрически заданной функцииСкачать

Расположение касательной в зависимости от значения её углового коэффициента
Рассмотрим несколько различных случаев значения углового коэффициента для касательной.
Если её угловой коэффициент, то есть, тангенс, равен нулю, то касательная расположена параллельно оси $OX$, а сама прямая принимает вид $y=b$.
Если тангенс положительный, то касательная образует острый угол с осью абсцисс, что значит, что вместе с ростом $x$ растёт и $y$.
В случае если тангенс отрицательный, прямая образует тупой угол с горизонтальной осью, а это значит, что с увеличением значения икса происходит уменьшение значения игрека.
Есть ещё один случай расположения касательной — параллельно оси $OY$, в этом случае её уравнение описывается как $x=c$, где $c$ — некая константа.
Другим числом, определяющим положение касательной, является число $b$, являющееся свободным членом в уравнении прямой $y=kx+b$. Число $b$ характеризует значение функции $y(x)$ в точке её пересечения с осью ординат, иначе говоря, оно есть не что иное, как значение уравнения касательной к графику функции в точке $x=0$.
Составить уравнение касательной в точке $x=3$ для графика функции $y(x)=2x^2+3x-6$.
Сначала найдём значение функции в точке $x=3$:
$y=2 cdot 3^2 +3 cdot 3 – 6 = 21$
Теперь определим значение производной для исследуемой функции:
Теперь получим значение углового коэффициента, для этого подставим $x=3$ в производную:
$y’(x)=4 cdot 3 + 3 = 15$
Подставим это значение в формулу для касательной $(2)$:
$y=15x-24$ — уравнение касательной получено.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 14 03 2021
📹 Видео
Уравнение касательнойСкачать

Уравнение касательной к графику функции в заданной точкеСкачать

Касательная к параболе. Построение касательнойСкачать

Что такое касательная | Осторожно, спойлер! | Борис Трушин |Скачать

Уравнение касательной к графику функции в задачах. Часть 3. Алгебра 10 классСкачать

Уравнения касательной и нормали к кривойСкачать

Часть 4: Общее уравнение КасательнойСкачать

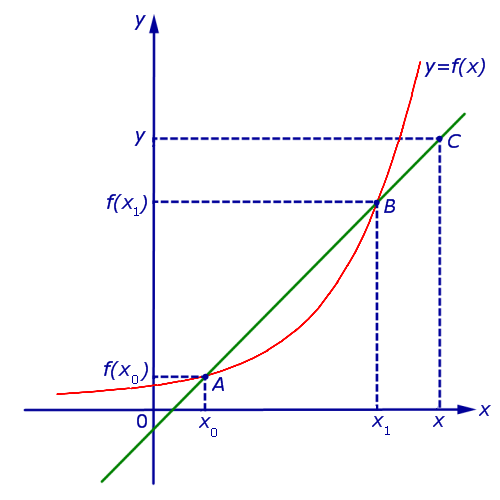 Рисунок 2. Секущая прямая на графике функции.
Рисунок 2. Секущая прямая на графике функции.