В 11-ом задании ОГЭ по математике идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции и математическим выражением (формулой). В задании сопоставляется различная информация о функциях. Необходимо находить и использовать в выполнении задания область определения функции, ее промежутки возрастания и убывания, промежутки знакопостоянства, нули функции, уметь читать графики функций. Работать надо с функциями, описывающими прямую пропорциональную зависимость, линейными функциями, гиперболами, квадратичными функциями.
Хотя на самом экзамене мы ожидаем работу именно с графиками функций, тем не менее в некоторых заданиях дается вместо рисунков их описание. Это делается, чтобы подчеркнуть те детали, на которые надо обратить внимание при работе с графиками функций.
Задание 11 несложное, тем не менее последние задания придуманы таким образом, чтобы любознательным школьникам было над чем подумать.
Ответом в задании 10 является набор цифр, описывающий соответствие между различными объектами.
- Теория к заданию №11
- Разбор типовых вариантов задания №11 ОГЭ по математике
- Первый вариант задания (параболы)
- Второй вариант задания (гиперболы)
- Третий вариант задания (линейный график)
- Экзамен по алгебре в 9-м классе «Функции»
- Задания ОГЭ на анализ графиков Начало
- Изученные функции и их графики.
- Задания на соответствие графика и формулы функции.
- Линейная функция. Прямая линия.
- График линейной функции, его свойства и формулы
- Понятие функции
- Понятие линейной функции
- Свойства линейной функции
- Построение линейной функции
- Решение задач на линейную функцию
- 🔥 Видео
Теория к заданию №11
Так как в данном задании речь идет о функциях и их графиках, приведем основные понятия и формулы.
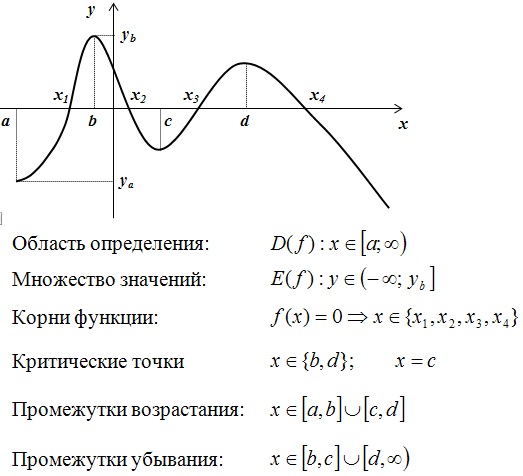
На произвольном примере ознакомимся с исследованием функции:
- область определения и множество значений
- корни и критические точки
- промежутки возрастания убывания
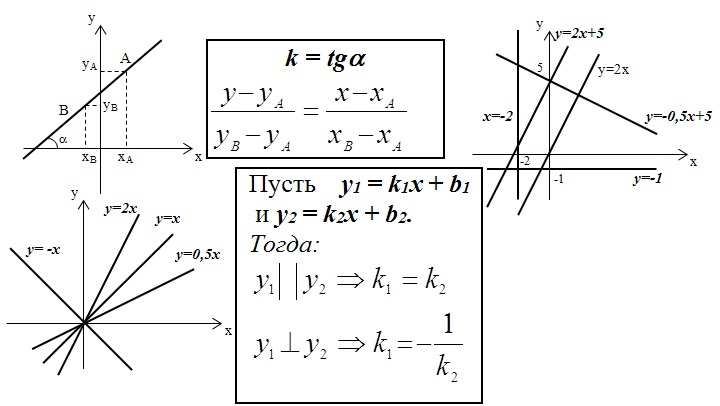
Теперь рассмотрим данный материал на линейной функции:
y = kx + b
где k – угловой коэффициент, b – свободный член
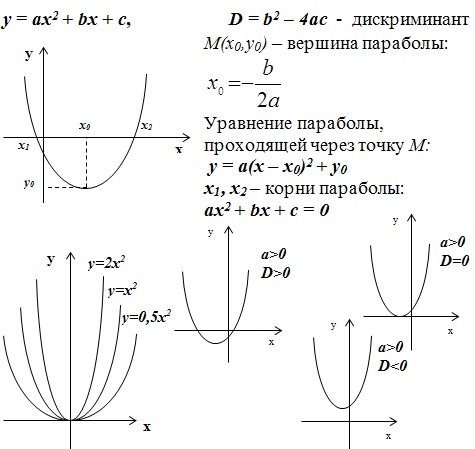
Рассмотрим случай квадратичной функции:
Также вспомним, что такое коренная функция и модуль:
Я разобрал три случая — случай с параболой и влияние коэффициентов на вид параболы — в первом примере. Во втором примере разобрана гипербола и общие закономерности зависимости общего вида графика от математического выражения. Третий случай рассматривает прямую и варианты её построения в зависимости от коэффициентов.
Разбор типовых вариантов задания №11 ОГЭ по математике
Первый вариант задания (параболы)
На рисунках изображены графики функций вида
Установите соответствие между знаками коэффициентов a и c и графиками функций.
В) a > 0, c 0, то ветви направлены вверх, а если a 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
Из всего вышеперечисленного можно найти ответ:
Второй вариант задания (гиперболы)
Установите соответствие между функциями и их графиками.
Решение:
В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
- если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
- если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
- чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости
- чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
Третий вариант задания (линейный график)
Установите соответствие между функциями и их графиками.
Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Экзамен по алгебре в 9-м классе «Функции»
Разделы: Математика
№1. Найдите все значения k, при которых прямая y=kx пересекает в трех различных точках график функции
Построим график данной функции. Прямые y=2x+1 и
y=2x-3 параллельны ,т.к. у них одинаковый угловой коэффициент , равный 2. Прямая y= — 1 параллельна оси абсцисс.
| y=2x+1, | y=2x — 3. |
| y(0)= 1, y(-1)= -1, | y(0)= — 3, y(1)= — 1. |
Прямая n задана уравнением y=2x. Для нахождения уравнения прямой l необходимо подставить координаты точки А(-1; -1) в уравнение y=kx.
-1=(-1)k. Отсюда k=1. Уравнение прямой l имеет вид y=kx.
Для того чтобы искомая прямая m пересекала график данной функции в трех различных точках (рис.1), она должна располагаться между прямыми n и l. При этом 1
№2 Постройте график функции y = f(x), где
При каких значениях m прямая y = m имеет с графиком этой функции три общие точки?
1. Графиком функции 
а) Ветви параболы направлены вниз.
б)
(–1;2) – координаты вершины параболы.

(0;1) – координаты точки пересечения параболы и оси Оy(оси ординат).
2. Графиком функции 
а) Ветви параболы направлены вверх.
б)


(0; – 5) – координаты точки пересечения параболы и оси Оy(оси ординат).
Найдём дополнительные точки для точного построения графика функции 
Найдём дополнительные точки для точного построения графика функции 
График данной функции (рис.2) только в трёх точках пересекают прямые
№ 3. Постройте график функции y= ¦ (x) , где
При каких значениях m прямая y = m имеет с графиком этой функции две общие точки?
Построим график данной функции. Для этого проведем исследования.
1. Графиком функции y= — x 
x


Определим точки пересечения параболы с осями координат:
x=0, y = -3; y=0, x

2. Графиком функции y= x + 1 является прямая.
y ( — 1 )= 0 , y (1) = 2.
3. Графиком функции y= 
График данной функции (рис.3) только в двух точках пересекает прямая y=0 и прямые y=m при 1
№ 4. Постройте график функции y = 
При каких значениях x выполняется неравенство y ? 3 ?
Найдем область определения функции:
2x — x




Преобразуем выражение, задающее функцию:
y = 
x


Построим прямую y= -(x + 1)= — x – 1 и “ выколем ” на ней точки, абсциссы которых равны 0 и 2 (рис.4).
y(- 4) = 3, y(0) = -1, y( 2) = -3.
— 4
x 2.
Ответ: [- 4; 0) E (0; 2) E (2; + ? ).
№ 5. Постройте график функции y= 
1. Найдем область определения данной функции:
x

x


Значит, областью определения является множество всех действительных чисел , кроме – 4 и – 2.
2. Для разложения числителя на множители решим уравнения :
а) x

x



3. Упростим данную функцию:
y= 

4.Исследуем полученную квадратичную функцию: графиком функции y = x


5. Построим параболу и “выколем” на ней точки, абсциссы которых равны — 4 и – 2, поскольку при этих значениях переменной исходная функция не определена (рис.5).
№ 6. Постройте график функции y= 
1. Найдем область определения данной функции:
2. Упростим данную функцию:
y=


3. Построим прямую y=x+1 на промежутках (- 1; — 1) и (1; + 
№ 7. Задайте аналитически функцию, график которой изображен на рисунке 7.
Ломаная состоит из двух звеньев, одно из них является графиком линейной функции y=kx+b при x 
В каждом случае необходимо найти k и b.
Для этого необходимо на каждом из звеньев выбрать по две точки, подставить их координаты в уравнение линейной функции и решить две получившиеся системы уравнений относительно k и b.
1)На левом звене возьмем точки с координатами (-2;0) и (2; -6).

Получим уравнение прямой y= -1,5 x–3 при x 
2) На второй части ломаной возьмем точки с координатами (2; — 6) и (4;0).

Получим уравнение прямой y= 3x – 12 при x > 2.
Зададим теперь заданную графически функцию аналитически:
Видео:Как построить график линейной функции.Скачать

Задания ОГЭ на анализ графиков
Начало
Если возникают вопросы — обращайтесь через форму для письма, рисунок конверта кликабелен.
Узнайте, как можно поддержать сайт и помочь его развитию.
- Изученные функции и их графики.
- Задания на соответствие графика и формулы функции в случае функций разных видов.
- Линейная функция. Прямая линия.
- Квадратичная функция. Парабола.
- Гипербола.
Видео:Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать

Изученные функции и их графики.
К концу учебного года в 9-ом классе вы успели изучить следующие функции:
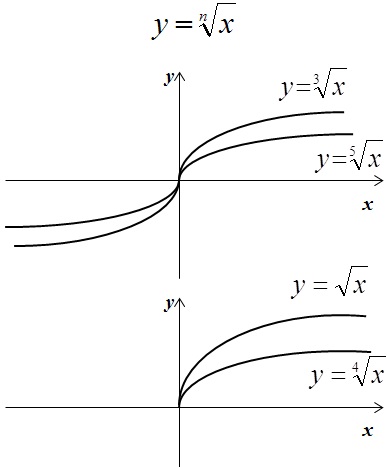
(y = kx+b) — линейная функция. Графиком является прямая линия. Коэффициент (k) задаёт тангенс угла наклона к оси (Ox). Если (k>0), прямая наклонена под острым углом к оси, если (k (y = dfrac) График этой функции называется гиперболой. Его легко «узнать в лицо», потому что на данный момент это единственная хорошо изученная функция с разрывом. Так как на 0 делить нельзя, то график не может пройти через эту точку, иными словами, пересечь ось (Oy), поэтому состоит из двух отдельных ветвей. Коэффициент (k) показывает насколько далеко отстоят вершины ветвей гиперболы от начала координат, а знак коэффициента (знак перед дробью) показывает в каких четвертях расположены ветви гиперболы. Если (k>0), то в первой и третьей, если (k (y = ax^2+bx+c) — квадратичная функция. Графиком функции является парабола. Коэффициент (a) задаёт направление. Если (a>0), ветви параболы направлены вверх, если (a (y = sqrt) По внешнему виду этот график похож на повёрнутую на 90 градусов половинку параболы. Это, действительно, она и есть, потому что квадратный корень является обратной функцией для квадратичной функции. Влияние коэффициентов (a) и (b) на положение графика заметно, прежде всего, по его сдвигу вдоль оси (Ox). График должен быть расположен так, чтобы его область определения совпадала с ОДЗ выражения, т.е. (ax+b ge 0.)
Ещё подробнее повторить графики функций вы сможете, если перейдёте к сводной таблице и воспользуетесь помещенными там ссылками на другие статьи сайта и видео на youtube-канале Mathematichka.
Видео:7 класс, 8 урок, Линейное уравнение с двумя переменными и его графикСкачать

Задания на соответствие графика и формулы функции.
Задачи, в которых приведены графики функций разных типов, я считаю самыми лёгкими в этом задании. Давайте рассмотрим несколько примеров, и вы в этом убедитесь.
Задача 1. Установите соответствие между графиками функций и формулами, которые их задают
На рисунке всего один график прямая линия. Ищем среди формул ту, которая содержит (x) только в первой степени. Смотрим, чтобы в этой формуле не было квадрата и переменной в знаменателе. Такая формула только одна, это формула (3); y=-2x). Делаем вывод: графику Б) соответствует формула 3).
Среди формул только одна содержит (x^2) (формула 4), и только один график непрерывная кривая линия симметричная относительно вертикальной прямой, проведенной через её вершину. Это парабола – график В). Вывод: графику В) соответствует формула 4).
Остался один график с разрывом. Две отдельных ветви содержит график А) – гипербола. Но у нас две формулы с (x) в знаменателе. Придётся выбирать.
На графике А) ветви гиперболы расположены во второй и четвёртой координатных четвертях, где знаки координат (x и y) не совпадают, поэтому перед дробью в формуле гиперболы должен быть знак минус. Но оказалось, что этой приметы недостаточно, так как минус есть в обеих формулах.

Пусть (x = 1), тогда по формуле 1) получим (y = -dfrac = -4), а по формуле 2) получим (y = -dfrac = -2). Проводим на рисунке вертикальную линию (x = 1) до пересечения с графиком и смотрим значение (y). Получилось (y = -4), значит верна первая формула. Вывод: графику А) соответствует формула 1).
Ответ:
| А | Б | В |
| 1 | 3 | 4 |
Ответы и решения некоторых задач временно скрыты. Это задачи для самостоятельного решения. Чтобы посмотреть ответы, воспользуйтесь соответствующими кнопками. Но предварительно попробуйте решить задачу самостоятельно.
Задача 2. Установите соответствие между функциями и их графиками.
На графике 1) линия с разрывом, следовательно в формуле есть (x) в знаменателе. Вывод: графику 1) соответствует формула А).
На графике 2) изображена прямая линия. Осталась только одна формула, где (x) в первой степени умножен на число (dfrac = dfraccdot x). Вывод: графику 2) соответствует формула В).
Два оставшихся графика нелинейны, т.е. кривые линии. Формула Б) представляет собой квадратный трёхчлен. Следовательно, график должен быть параболой. Мы знаем, что парабола симметрична относительно линии, проходящей через вершину. График 3) обладает этим свойством, а на графике 4) такую линию провести невозможно. Вывод: формула Б) соответствует графику 3).
Замечение. Проверку ответа можно сделать «по единичке», т.е. задать какое-либо значение (x), подставить его в формулы, вычислить значения (y) и найти соответствующие точки на графике. Но решить задание в буквальном смысле по единичке, т.е. подставить (x = 1) в формулу Б), а затем найти на графиках 3) и 4) ординаты точек с абсциссой 1, не получится. Потому что во всех случаях будет (y = 2). Выбор не состоится.
Ответ:
| А | Б | В |
| 1 | 3 | 2 |
Задача 3. Установите соответствие между графиками функций и формулами, которые их задают.
Координатные плоскости здесь представлены без клеточек. Проверить принадлежность точек не получится, выбираем только по внешнему виду графиков.
Прямая линия олна – А). Её формула 1) содержит просто (x).
Симметричная кривая на графике В) – парабола. Формула 2) содержит (x^2).
На среднем графике кривая линия похожа на перевёрнутую половинку параболы. Это график функции 3) квадратный корень.
Ответ:
| А | Б | В |
| 1 | 3 | 2 |
Видео:7кл. Постройте график уравнения x+y=5Скачать

Линейная функция. Прямая линия.
Задача 4. Установите соответствие между графиками функций и формулами, которые их задают.
Все графики – прямые линии и все формулы имеют вид (y = kx + b). Выбираем по наклону к оси (Ox) и точке пересечения с осью (Oy).
На графике В) прямая никак не наклонена к оси (Ox), она ей параллельна. Следовательно, угол наклона равен 0, тангенс угла наклона равен 0, угловой коэффициент (k=0), и (y = kx + b = 0cdot x + b = 0 + b = b.) Таким образом, формула, которая задаёт прямую, параллельную оси абсцисс, не должна содержать (x). Здесь такая формула под номером 3.
В двух оставшихся графиках наклон на глаз кажется примерно одинаковым. Поэтому начнём с точки пересечения с с осью (Oy). Вспомним, что для точек, расположенных на этой оси, (x=0), поэтому (y = kx + b = kcdot0 + b = 0 + b = b.) Таким образом, высота точки пересечения графика с этой осью показывает значение коэффициента (b) в формуле функции. На первом графике пересечение при (y=2), подходит формула (2); y = x+2.) На втором – при (y=0), подходит формула (1); y = 2x,) так как (2x = 2x+0.)
Сделаем проверку по единичке для графиков А) и Б).
При (x=1) по формуле 2) получим (y = 1 + 2 = 3). Если мы правильно установили соответствие, то точка с координатами (1;3) должна лежать на графике А).
При (x=1) по формуле 1) получим (y = 2cdot1 =2). Если мы правильно установили соответствие, то точка с координатами (1;2) должна лежать на графике Б).
Отметим эти точки на указанных графиках. Точки «не промахнулись», значит задача решена верно.
Ответ:
| А | Б | В |
| 2 | 1 | 3 |
Итак, все графики, которые задаются формулой (y = b), т.е. формулой, содержащей (y) и число, но не содержащей (x), представляют собой прямые линии, параллельные оси (Ox). Все графики, которые задаются формулой (y = kx), т.е. формулой, содержащей (x) в виде одночлена первой степени, представляют собой прямые линии, проходящие через начало координат. Эти выводы нужно запомнить на будущее не только, чтобы быстрее решать это задание ОГЭ, но и для задания на графики во второй части экзаменационного варианта.
Задача 5. Установите соответствие между функциями и их графиками.
Прямые на графиках 1) и 2) имеют одинаковый наклон. Одинаковый угловой коэффициент (k = 2) мы видим в формулах Б) и В). Методом исключения делаем вывод, что для графика 3) остаётся формула А).
Теперь, чтобы установить соответствие между графиками 1) и 2) и формулами Б) и В) смотрим на точку пересечения с осью (Oy). На первом графике она находится ниже оси абсцисс, что говорит о том, что в формуле коэффициент (b) имеет отрицательное значение. Смотрим: (b = -6) в формуле Б). Вывод: формула Б) соответствует графику 1), тогда формула В) соответствует графику 2).
Проверка по единичке: [А); y = -2cdot1+6 = 4;;; Б); y = 2cdot1-6 = -4;;; В); y = 2cdot1+6 = 8]
Как и предполагалось, (y = 4) на графике 3), (y = -4) на графике 1) (y = 8) на графике 2).
Ответ:
| А | Б | В |
| 3 | 1 | 2 |
Задача 6. На рисунке изображены графики функций вида (y = kx+b.) Установите соответствие между графиками линейных функций и угловыми коэффициентами прямых.
[1); -1;;; 2); -1,25;;; 3); 3;;; 4);0,8] В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В | Г |
Угловой коэффициент равен тангенсу угла наклона прямой к оси (Ox.) На данный момент мы знаем, что тангенс определён в прямоугольном треугольнике, как отношение противолежащего катета к прилежащему. Поэтому, прежде всего, надо начертить прямоугольные треугольники такие, что их гипотенузы лежат на заданных прямых, а катеты проходят по клеточкам. Вершины этих треугольников обязательно должны находиться в узлах клеточек, иначе будет трудно определить длины катетов. Размер треугольника может быть произвольным, «приклеить» его к прямой можно в любом удобном месте.
Угол наклона прямой по определению отсчитывается от положительного направления оси абсцисс (оси (Ox)), поэтому в наших треугольниках противолежащий катет всегда параллелен оси (Oy) (считаем клеточки по вертикали), а прилежащий – оси (Ox) (считаем клеточки по горизонтали).
Если прямая образует с положительным направлением оси абсцисс тупой угол, то угловой коэффициент будет со знаком минус. Поскольку линии клеток параллельны, то можно смотреть угол между прямой и правой частью горизонтальных линий сетки, как показано на рисунке.
Итак, вычисляем угловые коэффициенты по чертежу
[А); k = frac = 0,8; ;;; Б); k = -frac = -1,25; ;;; В); k = frac = 3; ;;; Г); k = -frac = -1 ] и сравниваем с предложенными значениями. [1);-1;;; 2);-1,25;;; 3); 3 ;;; 4);0,8.]
Ответ:
| А | Б | В | Г |
| 4 | 2 | 3 | 1 |
На эту тему также можно посмотреть видеоуроки на странице Линейная функция или на youtube-канале Mathematichka.
Видео:График линейного уравнения с двумя переменными, 7 классСкачать

График линейной функции, его свойства и формулы
О чем эта статья:
Видео:Как построить график функции без таблицыСкачать

Понятие функции
| Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. |
|---|
Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:
Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.
Графический способ — наглядно. Его мы и разберем в этой статье.
| График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу. |
|---|
Видео:Определение графика линейной функции по его формулеСкачать

Понятие линейной функции
| Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент. |
|---|
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Нам дана функция: у = 0,5х — 2. Значит:
если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0 и т. д.
Для удобства результаты можно оформлять в виде таблицы:
| х | 0 | 2 | 4 |
| y | -2 | -1 | 0 |
Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.
| Функция | Коэффициент k | Коэффициент b |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.
Видео:Все графики функций за 20 секундСкачать

Свойства линейной функции
Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит, y = b — четная;
b = 0, k ≠ 0, значит, y = kx — нечетная;
b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;
b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (−b/k; 0);
ось ординат OY — в точке (0; b).
x = −b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).
При k 0, то этот угол острый, если k
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
если k > 0, то график наклонен вправо;
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Если k > 0 и b
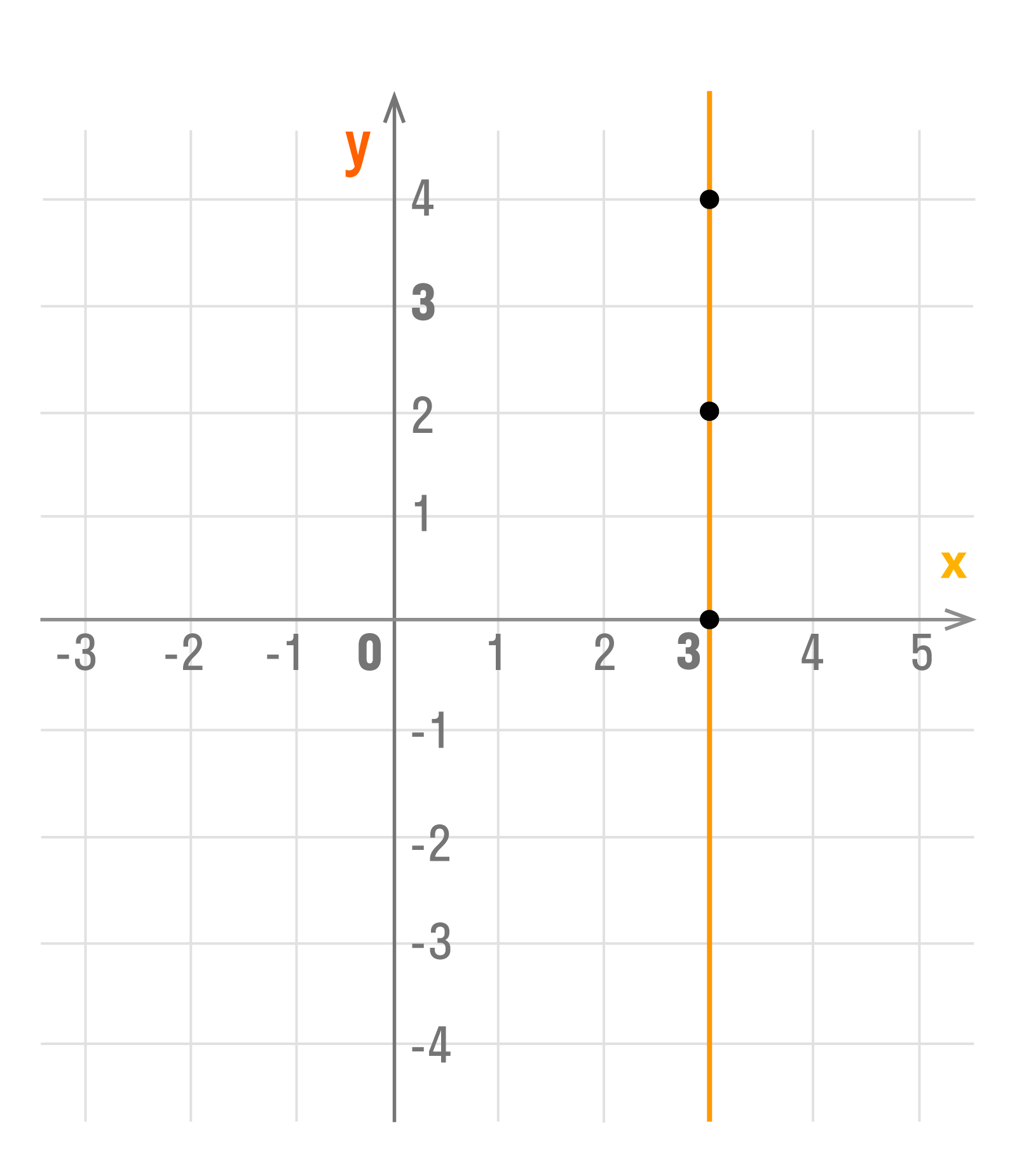
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Видео:ГРАФИК ЛИНЕЙНОГО УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСС видеоурокСкачать

Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Ответ: уравнение прямой y = 3x — 2.
🔥 Видео
Прямая y = 3x + 1 является касательной к графику функции f(x)= ax в квадрате + 2x + 3. Найдите a.Скачать

Как запомнить графики функцийСкачать

Как строить графики без таблицСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

7 класс, 35 урок, Графическое решение уравненийСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Линейная функция и её график. Алгебра, 7 классСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать
















 x 2.
x 2.