Идеальным называется газ, в котором межмолекулярные силы взаимодействия отсутствуют.
Свойства идеального газа:
- — размерами молекул газа по сравнению с размерами сосуда, в котором они находятся можно пренебречь, т.е. их можно считать материальными точками;
- — молекулы газа являются свободными. Это значит, что до столкновения с другими молекулами или со стенками сосуда, содержащего газ, они движутся прямолинейно и равномерно, как тела, неподверженные действию каких-либо сил;
- — столкновения молекул друг с другом или со стенками сосуда, содержащего газ, являются абсолютно упругими. Совершая движение молекулы, приближаются к стенкам сосуда на достаточно малые расстояния. Молекулы могут также подойти достаточно близко и друг к другу. В этом случае между молекулами газа или между молекулой газа и молекулами вещества стенки возникают силы взаимодействия, которые очень быстро убывают с увеличением расстояния. Под действием этих сил молекулы газа изменяют направление своего движения. Процесс изменения направления движения называется столкновением.
Физические величины, служащие для характеристики состояния газа называются параметрами состояния.
Важнейшими параметрами состояния идеального газа являются температура, давление, объем.
Газовые законы справедливы лишь для идеальных газов. Всякий реальный газ по мере убывания его плотности все больше приближается к идеальному. Это происходит, если газ имеет низкую плотность, т.е. средние расстояния между молекулами значительно превышают их диаметр. Последнее условие выполняется при достаточно малых давлениях и не слишком низких температурах (по мере приближения к абсолютному нулю температур газы переходят в жидкую фазу, для которой характерно относительно большое взаимодействие молекул между собой).
Соотношение, дающее связь между параметрами какого-либо тела, называется уравнением состояния.
Для изотермического процесса справедлив закон, установленный англичанином Бойлем (1662 г.) и французом Мариоттом (Закон Бойля-Мариотта).
Для данной массы газа при t = const давление изменяется обратно пропорционально объему
P·V = const, при m = const и T = const
Для одинаковой массы газа при одной и той же температуре газ занимает тем больший объем, чем ниже давление:
Изменяя температуру газа, Гей-Люссак нашел, что для данной массы газа при постоянном давлении объем растет линейно с температурой (Закон Гей-Люссака). Такой процесс получил название изобарического.
Vt = V0 · (1+a·t), при m = const и p = const
Физический смысл универсальной газовой постоянной в том, что она показывает, какую работу совершает один моль идеального газа при изобарном расширении при нагревании на 1 К (R = 8,31 ДжДмоль * К)).
При постоянном объеме для данной массы газа давление растет линейно с температурой (закон Шарля). Данный изопроцесс называется изохорическим.
pt = p0·(1+a·t), при m = const и V = const
Объединив законы Бойля-Мариотта и Гей-Люссака, получается уравнение состояния идеального газа, связывающее все его параметры. Это уравнение называется уравнением состояния идеального газа (уравнение Клайперона).
PV / T = const, при m = const
Если массу газа удвоить при постоянном объеме и Т (или соединить два объема равных масс), то отношение увеличивается вдвое. Поэтому Клайперон указал, что const = Bm, где В — индивидуальная газовая постоянная, зависящая от природы газа.
Менделеев несколько видоизменил закон Клайперона, объединив его с законом Авогадро (если Р и Т одинаковы, то киломоли разных газов занимают одинаковый объем — Vm). PVm /Т = R = const — одинакова для всех газов. R — универсальная газовая постоянная.
PVm = ТR — уравнение Менделеева-Клайперона для киломоля газа. Для произвольной массы газа уравнение Менделеева — Клайперона примет вид:
где m/m = n — число киломолей.
где r — плотность вещества
Рассмотрим смесь идеальных газов, заключенных в объеме V при температуре Т. Обозначим массы и молекулярные веса их:
Парциальным давлением газа, входящего в газовую смесь, называется то давление, которое имел бы этот газ, если бы он один занимал весь объем сосуда при данной температуре.
Тогда суммарное давление газовой смеси равно сумме парциальных давлений входящих в нее газов — закон Дальтона.
где pi = (mi/mi)·R·T/V — парциальное давление iой компоненты в смеси газов.
Из уравнения Менделеева-Клайперона можно получить любой из газовых законов.
Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Физическая химия: конспект лекций
Данное учебное пособие предназначено для студентов химических факультетов высших учебных заведений педагогического и технического направления. Изложены основные концепции и процессы, составляющие современную физическую химию. Материал соответствует государственному стандарту. Пособие рекомендовано в помощь студентам при подготовке к экзаменам.
Оглавление
- Введение
- ЛЕКЦИЯ № 1. Идеальный газ. Уравнение состояния реального газа
- ЛЕКЦИЯ № 2. Химическая термодинамика
Приведённый ознакомительный фрагмент книги Физическая химия: конспект лекций предоставлен нашим книжным партнёром — компанией ЛитРес.
ЛЕКЦИЯ № 1. Идеальный газ. Уравнение состояния реального газа
1. Элементы молекулярно-кинетической теории
Науке известно четыре вида агрегатных состояний вещества: твердое тело, жидкость, газ, плазма. Переход вещества из одного состояния в другое называют фазовым переходом. Вода, как известно, существует в трех агрегатных состояниях: в жидком (вода), твердом (лед), газообразном (пар). Это различие между тремя агрегатными состояниями определяется межмолекулярным взаимодействием и степенью сближения молекул.
Газ — агрегатное состояние вещества, в котором молекулы движутся хаотически, расположены на большом расстоянии друг от друга. В твердых телах расстояния между частицами малы, сила притяжения соответствует силе отталкивания. Жидкость — агрегатное состояние, промежуточное между твердым и газообразным. В жидкости частицы расположены близко одна к другой и могут перемещаться друг относительно друга; жидкость, как и газ, не имеет определенной формы.
Каждое из этих состояний можно описать набором некоторых параметров: например, состояние газа достаточно полно описывается тремя параметрами: объем, давление, температура.
Комбинация трех параметров, достаточно легко измеряемых, уже с середины ХVII века, когда были созданы барометры и термометры, хорошо описывает состояние газовой системы. Именно поэтому изучение сложных многоатомных систем началось с газов. У истоков наук химии и физики стоял Р. Бойль.
2. Уравнение состояния идеального газа
Изучение эмпирических газовых законов (Р. Бойль, Ж. Гей-Люссак) постепенно привело к представлению об идеальном газе, поскольку обнаружилось, что давление данной массы любого газа при постоянной температуре обратно пропорционально объему, занимаемому этим газом, и термические коэффициенты давления и объема с высокой точностью совпадают для различных газов, составляя, по современным данным, 1/273 град –1 . Придумав способ графического представления состояния газа в координатах «давление — объем», Б. Клапейрон получил объединенный газовый закон, связывающий все три параметра:
где коэффициент В зависит от вида газа и его массы.
Только через сорок лет Д. И. Менделеев придал этому уравнению более простой вид, записав его не для массы, а для единицы количества вещества, т. е. 1 кмоля.
где R — универсальная газовая постоянная.
Физический смысл универсальной газовой постоянной. R — работа расширения 1 кмоля идеального газа при нагревании на один градус, если давление не меняется. Для того, чтобы понять физический смысл R, представим себе, что газ находится в сосуде при постоянном давлении, и мы повысим его температуру на ΔT, тогда
Вычитая из (3) уравнение (2), получим
Если правая часть уравнения равна единице, т. е. мы нагрели газ на один градус, тогда
Поскольку P = F/S, а ΔV равно площади сосуда S, умноженной на высоту подъема его поршня Δh, имеем
Очевидно, что справа получим выражение для работы, и это подтверждает физический смысл газовой постоянной.
3. Кинетическая теория газов
Очень плодотворным в середине XIX века оказалось представление о молекулярном строении вещества. Когда была принята гипотеза А. Авогадро о том, что в киломоле любого вещества содержится одно и то же количество структурных единиц: 6,02 x 10 26 кмоля = 6,02 x 10 23 моля, поскольку молярная масса воды M(H2O) = 18 кг/кмоль, следовательно, в 18 литрах воды находится столько же молекул, сколько в 22,4 м 3 водяного пара. Это позволяет легко понять, что расстояние между молекулами газообразной воды (пара) значительно больше, в среднем на один порядок, чем в жидкой воде. Можно предположить, что это выполняется для любого вещества. Считая, что в газах молекулы движутся хаотически, можно вывести так называемое основное уравнение кинетической теории:
где Na — 6,02 x 10 26 кмоль = 6,02 x 10 23 моль — число Авогадро;
VM — молекулярный объем = 22,4 м 3 ;
m — масса одной молекулы;
v — скорость молекулы.
Преобразуем уравнение (4):
где Ek — энергия одной молекулы.
Видно, что справа стоит полная кинетическая энергия всех молекул. С другой стороны, сравнивая с уравнением Менделеева — Клапейрона, видим, что это произведение равно RT.
Это позволяет выразить среднюю кинетическую энергию молекулы газа:
где к = R / Na — постоянная Больцмана, равная 1,38 ґ 10– 23 кДж/кмоль. Зная кинетическую энергию молекулы, можно рассчитать ее среднюю скорость
Около 1860 г. Д. К. Максвелл вывел функцию, описывающую распределение молекул газа по скоростям. Эта функция имеет на графике вид характерной кривой с максимумом около наиболее вероятной скорости примерно 500 м/с. Важно заметить, что существуют молекулы со скоростями, превышающими этот максимум. С другой стороны, уравнение (6) позволяет сделать вывод об увеличении доли молекул с большими скоростями при нагревании газа. Спустя почти 60 лет гениальная догадка Д. К. Максвелла была подтверждена в опытах О. Штерна.
4. Уравнение состояния реального газа
Исследования показали, что уравнение Менделеева — Клапейрона не очень точно выполняется при исследовании разных газов. Голландский физик Я. Д. Ван-дер-Ваальс первым понял причины этих отклонений: одна из них состоит в том, что вследствие огромного числа молекул, их собственный объем в целом сравним с объемом сосуда, в котором находится газ. С другой стороны, существование взаимодействия между молекулами газа слегка искажает показание манометров, с помощью которых обычно измеряют давление газа. В итоге Ван-дер-Ваальс получил уравнение следующего вида:
где а, в — постоянные величины для различных газов.
Недостаток этого уравнения в том, что а и в должны быть измерены для каждого газа эмпирически. Преимущество в том, что оно включает область перехода газа в жидкую фазу при высоких давлениях и низких температурах. Осознание этого сделало возможным получать любой газ в жидкой фазе.
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Уравнения состояния реальных газов
Вопрос №1
Идеальный газ. Законы идеальных газов
Идеальным называется газ, у которого объемы молекул бесконечно малы и отсутствуют силы межмолекулярного взаимодействия. Молекулы идеального газа представляют собой материальные точки, взаимодействие между которыми ограничено молекулярными соударениями.
Любой реальный газ тем ближе к идеальному, чем ниже его давление и выше температура. Например, окружающий нас воздух можно считать идеальным газом. Понятие идеального газа и законы идеальных газов полезны в качестве предела законов реального газа.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
На практике часто приходится иметь дело с газами при невысоких давлениях, поэтому расчеты различных термодинамических процессов с достаточной степенью точности можно проводить по уравнениям идеального газа.
Закон Авогадро
Согласно этому закону, все газы при одинаковых температурах и одинаковом давлении содержат в одном и том же объеме одинаковое число молекул. Большую техническую значимость имеет следствие из закона Авогадро: объемы киломолей различных газов равны, если они находятся при одинаковых температурах и давлениях. При нормальных физических условиях (Т= 273,15 К, р = 760 мм рт. ст.) объем киломоля любого вещества равен Vµ=µν=22,4 м 3 /кмоль.Напомним, что киломолем называется количество вещества в килограммах, численно равное его молекулярной массе.
Этот закон был открыт независимо друг от друга английским физиком Р. Бойлем и французским ученым Э. Мариоттом. Ими было доказано, что при постоянной температуре газа произведение давления газа на его объем есть величина постоянная, т.е. при
рV= const и рv = const.
Закон Гей-Люссака
Этот закон устанавливает, что если в процессе нагрева или охлаждения газа давление подцерживается постоянным, то объем изменяется пропорционально абсолютной температуре, т.е. если
Р = const, то и v/ Т = const.
Если же мы рассмотрим процесс нагрева или охлаждения газа в сосуде постоянного объема (v= const), то р/Т = const.
Уравнение состояния идеального газа
Для 1 кг газа Клапейроном установлено уравнение состояния рv = RT, в котором газовая постоянная Rимеет для каждого газа свое постоянное значение. Измеряется Rв Дж/кг-К и имеет вполне определенный физический смысл — это работа, совершаемая 1 кг газа при его нагреве на один кельвин при постоянном давлении. Для газа с произвольной массой M/(кг) уравнение состояния имеет вид
Для одного киломоля вещества уравнение состояния (получено Д.И. Менделеевым) имеет вид рVµ =µRT, где µR— универсальная газовая постоянная, которая одинакова для всех газов и равна 8314 Дж/кмольК.
Во всех этих уравнениях давление подставляется в Па, температура — в К, объем — в м 3 и удельный объем — в м 3 /кг.
В резервуаре объемом 10 м 3 находится азот при избыточном давлении 100 кПа и при температуре 27 °С. Атмосферное давление равно 750 мм рт. ст. Требуется найти массу и плотность азота.
Выразим атмосферное давление в паскалях: рб = 10 5 Па.
Абсолютное давление газа равно:p =ри +рб = 100 • 10 3 + 10 5 = = 2 • 10 5 Па.
Газовая постоянная азота равна (µ = 28 кг/кмоль)
R = 8314/28 = 297 Дж/кгЧК. Масса газа равна
М =рV/RT= 2*10 5* 10/297 • (273,15 + 27) = 22,43 кг.
р = M/V= 22,43/10 = 2,243 кг/м 3 .
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
РЕАЛЬНЫЕ ГАЗЫ
Свойства реальных газов
Свойства реальных газов значительно отличаются от свойств идеальных газов, причем отличия тем значительнее, чем выше давление и ниже температура газа. Это объясняется тем, что молекулы реальных газов имеют конечный объем и между ними существуют силы межмолекулярного взаимодействия. Уравнение состояния 1 кг реального газа имеет вид
где z= φ(р, T) — коэффициент сжимаемости, который может быть как больше, так и меньше единицы.
При проведении термодинамических расчетов с реальными газами нужно учитывать зависимость внутренней энергии, энтальпии и теплоемкости не только от температуры, но и от давления газа. При одном и том же давлении какое-либо вещество в зависимости от температуры может находиться в разных состояниях.
Из физики известно, что любое вещество может находиться в твердом, жидком или газообразном состоянии. Эти состояния будем называть фазами, а процесс перехода из одного состояния в другое — фазовым переходом.
При определенных условиях могут существовать одновременно две фазы вещества, например, лед и жидкость, пар и жидкость. Если пар и жидкость находятся в состоянии равновесия, то пар называется насыщенным.
У всех веществ фазовые переходы происходят при определенных физических параметрах, поэтому рассмотрение свойств реальных газов можно начать на примере вещества, которое является основным рабочим телом в циклах тепловых электростанций, в том числе и атомных. Этим рабочим телом является вода, и не только потому, что она относительно дешева и нетоксична, а потому, что она обладает благоприятными для работы термодинамическими свойствами.
Рассмотрим диаграмму «v—p» воды и водяного пара, на которой изобразим границы между фазами (рис. 1.1). В области а находится в равновесии смесь льда и некипящей воды, в области Ь находится некипящая вода, в области с находится смесь кипящей воды и водяного пара, в области d— перегретый водяной пар. Прямой 1-2 показан изобарный процесс подвода теплоты.
Показанные на рис. 1.1 кривые называются пограничными; кривые, ограничивающие с двух сторон область с, называются левой и правой пограничными кривыми. Им соответствуют кипящая вода (левой) и сухой насыщенный пар (правой). Область между этими кривыми называется областью влажного насыщенного пара — в этой области находятся в равновесии сухой насыщенный пар и кипящая вода. Смесь сухого насыщенного пара и кипящей воды называют влажным насыщенным паром. Масса влажного насыщенного пара равна
где М’ — масса кипящей воды и М» — масса сухого насыщенного пара.
В дальнейшем все параметры, относящиеся к кипящей жидкости, будут иметь индекс «штрих» (р’, h’и т.д.), а все параметры, относящиеся к сухому насыщенному пару,— индекс «два штриха» (р’, h» и т.д.).
Температуру и давление насыщенного пара принято обозначать Тн и рн. В то же время в ряде литературных источников их обозначают Тs и рs (буква s является первой буквой английского слова sаturation — насыщение). Отношение массы сухого насыщенного пара к общей массе влажного насыщенного пара называется степенью сухости и обозначается х. Ясно, что на левой пограничной кривой х = 0, а на правой — х = 1. Разность <1-х) называется степенью влажности.
Чем выше давление пара, тем меньше расстояние по горизонтали между левой и правой пограничными кривыми, а при определенном давлении пара эти кривые смыкаются. Точка, в которой исчезают различия в свойствах кипящей жидкости и сухого насыщенного пара, называется критической (точка к на рис. 1.1).
Термические параметры различных веществ в критической точке различны. Эти параметры для ряда химических веществ приведены в табл. 1
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Таблица 1 Критические параметры веществ
| Вещество | Tкр, К | pкр,МПа | ρкр, кг/м 3 |
| Азот N2 | 3,40 | ||
| Водород Н2 | 33,2 | 1,29 | |
| Водяной пар H2O | 647,12 | 22,115 | |
| Кислород О2 | 5,05 | ||
| Ртуть Нg | — | ||
| Диоксид углерода СО2 | 7,38 |
При сверхкритическом давлении не может быть влажного насыщенного пара. Если давление пара больше критического и постоянно по величине (р > ркр), то при подводе (или отводе) теплоты физические параметры (удельный объем, энтальпия и др.) меняются плавно, в то же время наблюдается резкое изменение тепло-емкостей сp исvв тех процессах, где сверхперегретая вода переходит в сверхперегретый водяной пар.
Уравнения состояния реальных газов
Известно значительное число уравнений состояния реальных газов, и одна из самых удачных попыток была сделана Ван-дер-Ваальсом, который получил уравнение в виде
Слагаемое a/v 2 учитывает внутреннее давление, обусловленное силами взаимодействия молекул газа, а величина b— уменьшение объема, в котором движутся молекулы реального газа. Если по этому уравнению находить величины удельных объемов реальных газов, то уравнение (1) имеет три действительных корня при Т Ткр . Точность вычислений по этому уравнению невелика.
В самой общей форме уравнение состояния реальных газов имеет вид
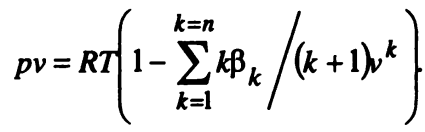
где 𝛽k — вириальные коэффициенты, зависящие от температуры газа.
Число членов ряда в уравнении (2) может быть достаточно велико, поэтому расчеты по этому уравнению вызывают значительные трудности.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
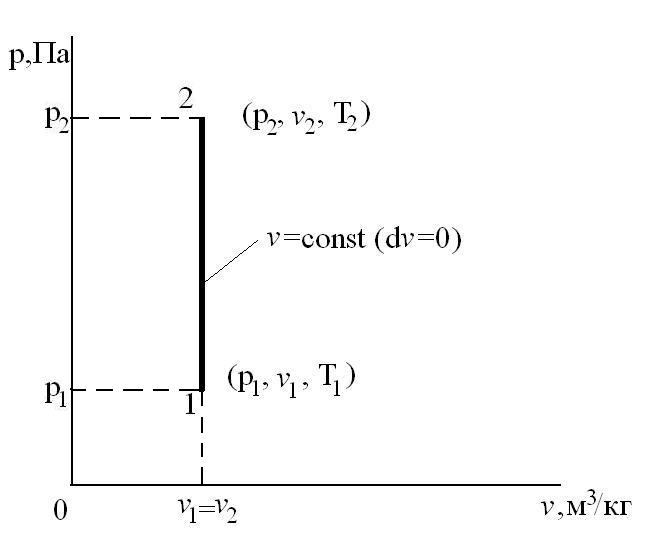
Изохорный процесс – это процесс сообщения или отнятия теплоты от газа при постоянном объеме v=const.
Этот процесс используется как подготовительный процесс в циклах.
Соотношение между параметрами для конечного участка процесса 1-2 определяется законом Шарля: 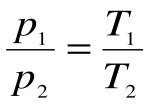
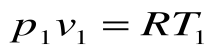
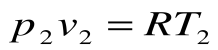
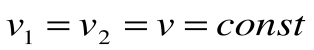
Поскольку работа расширения в этом процессе равна нулю: 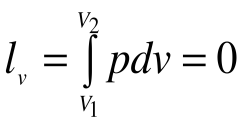
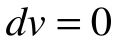
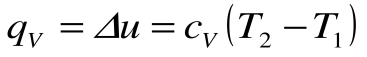
Таким образом, подведенная к газу в изохорном процессе теплота целиком идет на увеличение его внутренней энергии. Для ТП 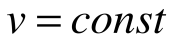


| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
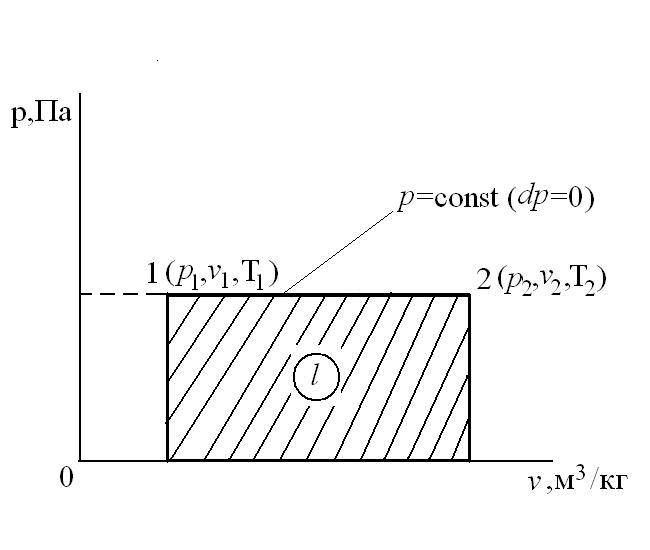
Изобарный процесс – это процесс сообщения или отнятия теплоты от газа при постоянном давлении р=const.
Соотношение между параметрами в процессе р=const: 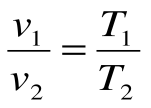


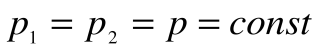
Работа расширения 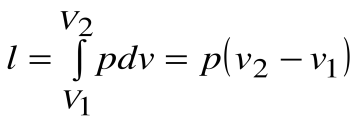
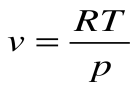
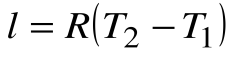
Следовательно, удельная газовая постоянная R— это работа, совершаемая 1кг газа в процессе p=const при его нагревании на один градус. Размерность R: Дж/кгК. Уравнение 1-го закона термодинамики в этом случае имеем вид:
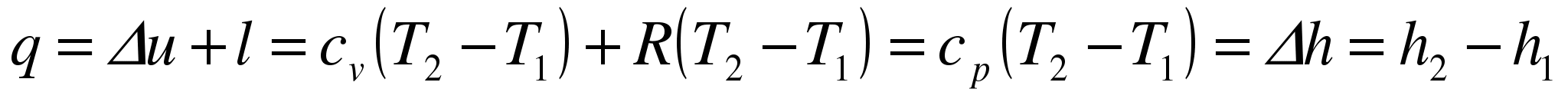
Таким образом, вся теплота, подведенная к газу в изобарном процессе, расходуется на увеличение его энтальпии.
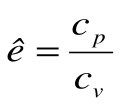
Коэффициент распределения теплоты в процессе р=const равен:
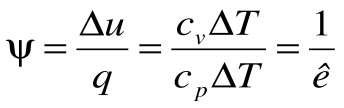
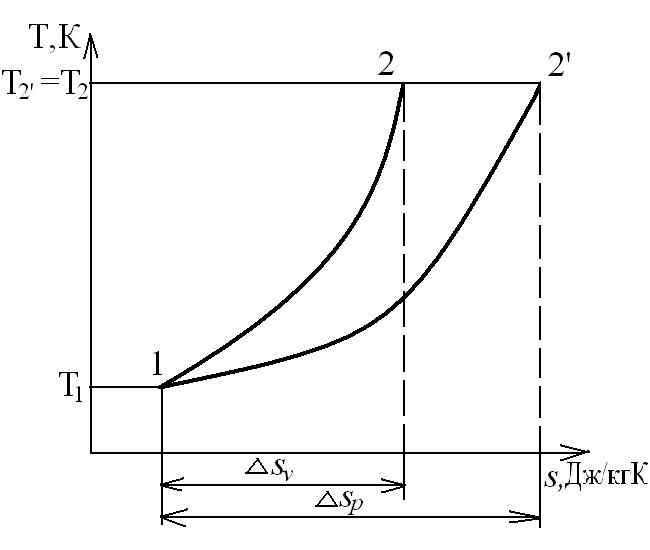
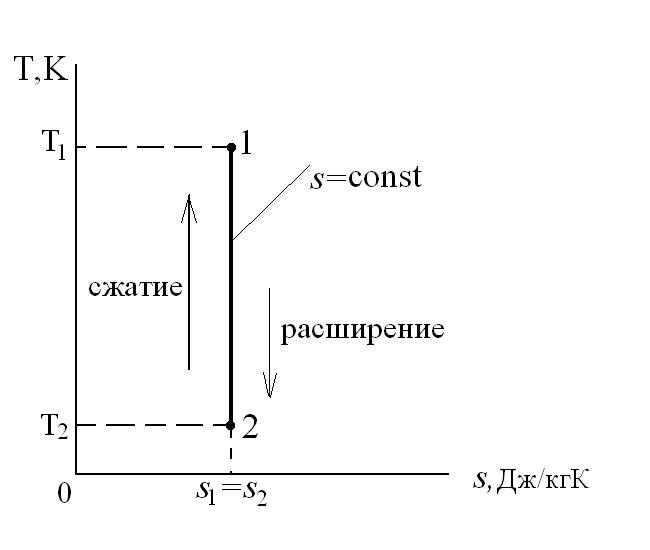
В T-s координатах взаимное положение изобары и изохоры имеет вид:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
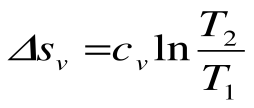
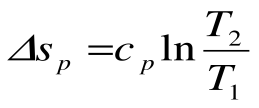
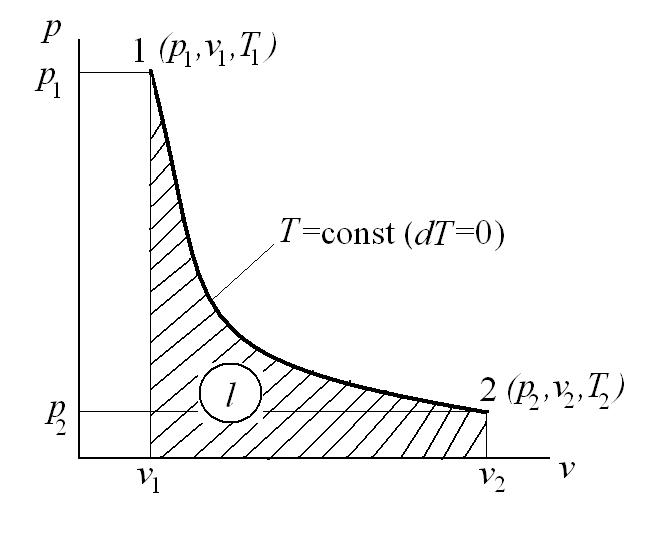
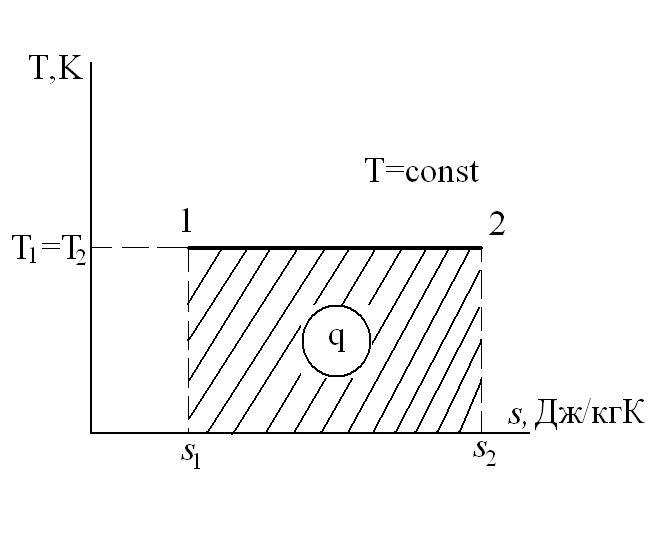
Изотермический процесс – это процесс сообщения или отнятия теплоты от газа при постоянной температуре
При Т=const из уравнения состояния 
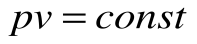
Тогда 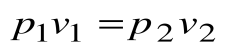
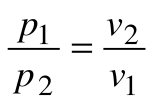
Из уравнения 1-го закона термодинамики 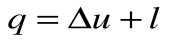
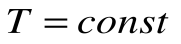
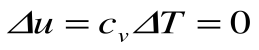
Изменение энтальпии в процессе T=const равно:
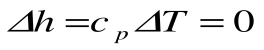
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Работа расширения 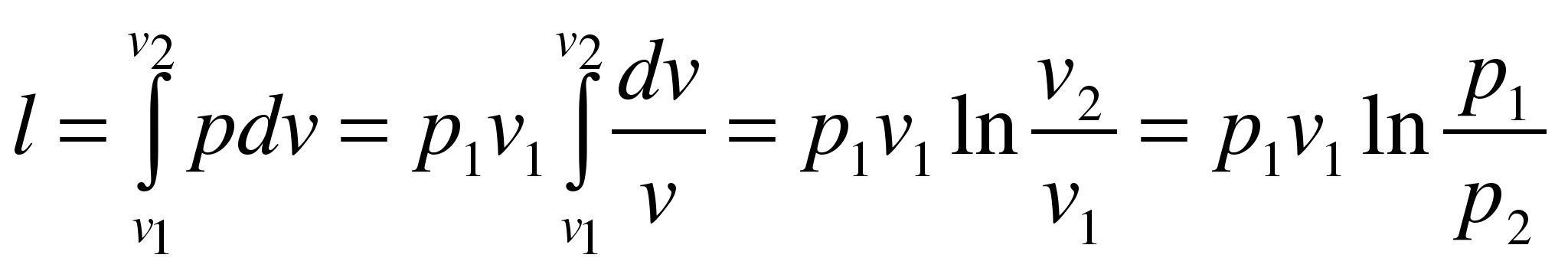
Коэффициент распределения теплоты
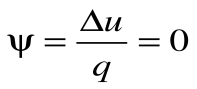
Тогда теплоемкость 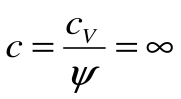
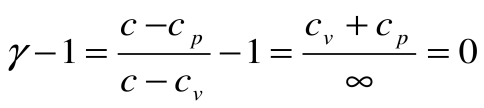
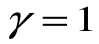
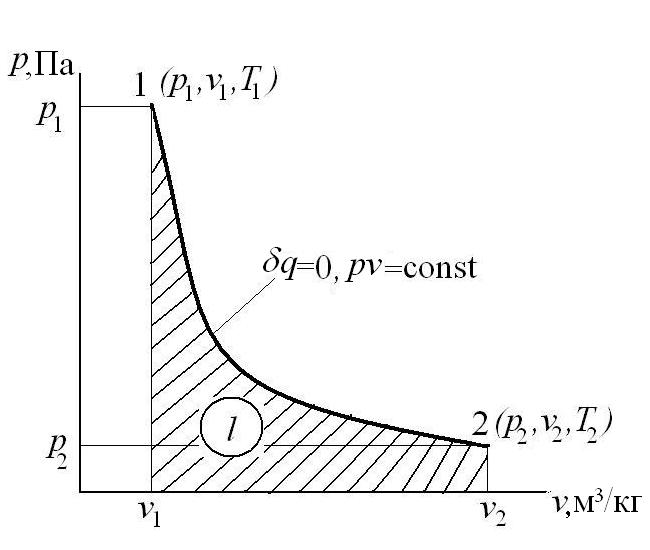
Адиабатный процесс – это процесс, протекающий без внешнего теплообмена, т.е. q=0 и 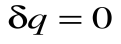
Если записать для этого случая уравнения 1-го закона термодинамики в виде:
1. 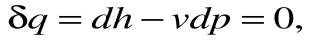
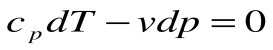
2. 
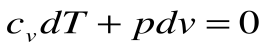

Тогда после интегрирования выражения 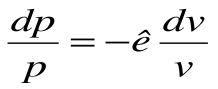

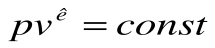
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
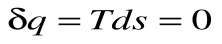
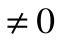
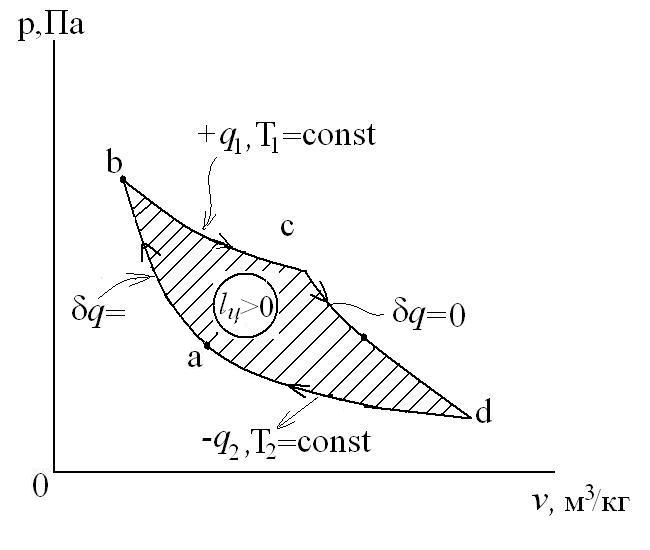
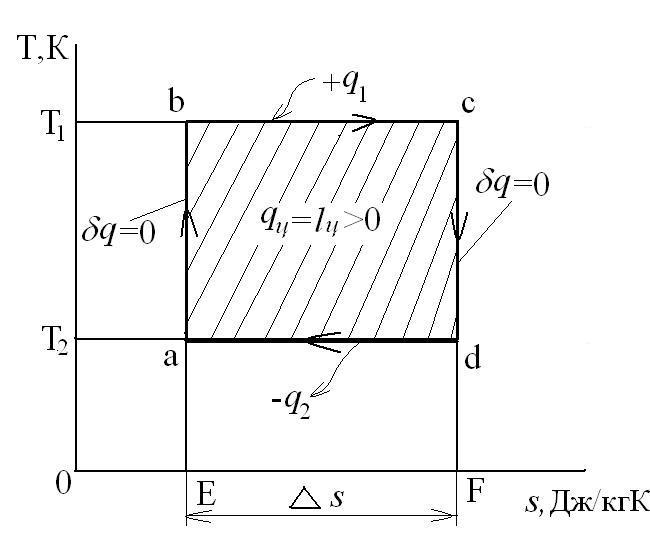
Для теплового двигателя цикл Карно – прямой цикл, состоящий из двух адиабат и двух изотерм, а для тепловых трансформаторов используется обратный цикл Карно. Тепловые машины, работающие по циклу Карно, имеют наибольшие значения термических кпд по сравнению с любым другим циклом при одинаковых предельных температурах цикла Т1 и Т2.
Рассмотрим прямой цикл Карно.
Графически в p-v и T-s координатах этот цикл можно представить в виде:
где ab – адиабатное сжатие ТРТ;
bc – подвод теплоты q1 в изотермическом процессе при Т1=const;
cd – адиабатное расширение ТРТ;
da – отвод теплоты 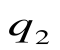
q1 = площадь bсFEb – теплота, затраченная на совершение цикла 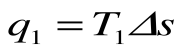
q2 = площадь adFЕa – теплота, отведенная в холодильник 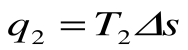
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Тогда термический кпд прямого цикла Карно будет равен:
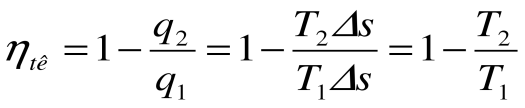
Таким образом, термический кпд цикла Карно зависит только от предельных температур источника и холодильника и не зависит от рода рабочего тела. (Первая теорема Карно). Температура Т1 и Т2 являются основными параметрами цикла Карно, которые полностью определяют этот цикл.
При Т1=Т2 термический кпд цикла Карно 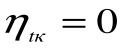
При Т2=0 или Т1= 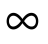
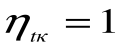
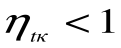
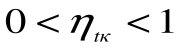
Любое заключение, вытекающее из анализа прямого цикла Карно, можно рассматривать как формулировку второго закона термодинамики.
В двух разобщенных между собой теплоизолированных сосудах А и В содержатся газы, в сосуде А – аргон, в сосуде В– водород, объем сосуда А– 150 л, сосуда В – 250 л. Давление и температура аргона – р1, t1, водорода – р2, t2. Определить давление и температуру, которые установятся после соединения сосудов и смешения газов. Теплообменом с окружающей средой пренебречь
🎥 Видео
Реальный газ Уравнение Ван-Дер-ВаальсаСкачать

Уравнение Ван-дер-Ваальса | Газы.Молекулярно-кинетическая теория | Химия (видео 8)Скачать

Уравнение Ван дер ВаальсаСкачать

Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Уравнение состояния идеального газаСкачать

Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

Газовые законы. Изопроцессы | Физика 10 класс #34 | ИнфоурокСкачать

Уравнение Ван-дер-Ваальса и опыт Джоуля и ТомсонаСкачать

Урок 195. Изотермы реального газаСкачать

ЕГЭ по физике. Теория #25. Идеальный газ. Уравнение состояния идеального газаСкачать

Уравнение Ван дер Ваальса. Часть 3. Внутренняя энергия реального газа. Фазовые переходы 1 рода.Скачать

Газовые законыСкачать

идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать

Лекция №2. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать

Идеальный и реальный газ | Газы.Молекулярно-кинетическая теория | Химия (видео 7)Скачать

Лекция №7 "Реальный газ"Скачать