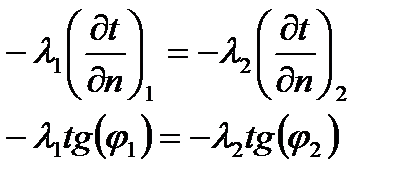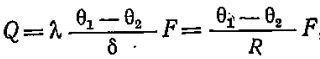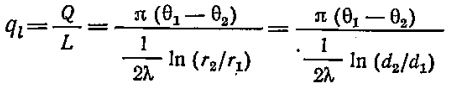Какое из приведенных уравнений является уравнением фурье

В 1807 году французский ученый Фурье доказал экспериментально, что во всякой точке тела (вещества) в процессе теплопроводности присуща однозначная взаимосвязь между тепловым потоком и градиентом температуры:

,

где Q – тепловой поток, выражается в Вт;

grad(T) – градиент температурного поля (совокупности числовых значений температуры в разнообразных местах системы в выбранный момент времени), единицы измерения К/м;

S – площадь поверхности теплообмена, м 2 ;

Градиент температуры получится характеризовать в виде векторной суммы составляющих по осям декартовых координат:

,

где i, j, k – ортогональные между собой единичные векторы, нацеленные по координатным осям.

Значит, данный закон устанавливает величину теплового потока при переносе тепла посредством теплопроводности.

Закон Фурье для поверхностной плотности теплового потока принимает вид:

.

Знак « минус» обозначает, что векторы теплового потока и градиента температуры разнонаправленные. Следует понимать, что теплота передается в направлении спада температуры.

И все же не лишним будет указать, что закон Фурье не принимает в расчет инерционность процесса теплопроводности, иначе говоря, в представленной модели колебание температуры в любой точке мгновенно распространяется на всё тело. Закон Фурье некорректно применять для характеристики высокочастотных процессов таких как, к примеру, распространение ультразвука, ударной волны.

Видео:Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Закон Фурье | Все это важно с 6 часто задаваемыми вопросами

Видео:Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Content

Видео:УМФ. Метод Фурье для параболического уравненияСкачать

Закон теплопроводности Фурье

Закон Фурье теплопроводности может иметь следующий вид:

«Скорость теплопередачи от материала или образца прямо пропорциональна площади поперечного сечения (перпендикулярной площади), через которую проходит тепло, и разности температур вдоль торцевых поверхностей материала».

Мы можем записать это утверждение математически как,

q = скорость теплопередачи в ваттах (Вт или Дж / с)

K = теплопроводность материала или образца (Вт / м · K)

A = Площадь поперечного сечения, через которую проходит тепло, в м 2

dT = разница температур между горячей и холодной сторонами в K (Кельвинах)

dx = Толщина материала в м (толщина между горячей и холодной стороной)

Самое важное: здесь в уравнении отрицательный знак означает, что тепло всегда течет в направлении уменьшения температуры.

Видео:5. Решение волнового уравнения на отрезке методом ФурьеСкачать

Уравнение закона Фурье

Уравнение закона теплопроводности получено выше. Он широко используется для решения задач теплопроводности и анализа. Суть уравнения остается прежней, но параметры меняются в зависимости от формы и положения объекта.

Видео:Классические точные аналитические методы решения уравнений гиперболического и параболического типаСкачать

Сферические координаты закона Фурье

Закон теплопроводности, примененный к цилиндру и уравнению, приведен ниже:

Здесь, в любом месте

r — радиус рассматриваемого цилиндрического участка,

Видео:AGalilov: Преобразование Фурье "на пальцах"Скачать

Цилиндрические координаты закона Фурье

Закон теплопроводности, применяемый к цилиндру и уравнению, приведен ниже:

в любом месте площадь A = 2πrL,

r — радиус рассматриваемого цилиндрического участка,

Видео:Уравнения математической физики. Решение гиперболического уравнения методом Фурье.Скачать

Эксперимент с законом Фурье

Перенос тепла проводимостью происходит за счет микроскопической диффузии и столкновений молекул или квазичастиц внутри объекта из-за разницы температур. Если мы видим микроскопически, то диффузный и сталкивающийся любой материал включает в себя молекулы, электроны, атомы.

Обычно у металлов есть свободная подвижность электронов внутри объекта. Это причина его хорошей проводимости.

Рассмотрим двухблочный A и B,

Блок А очень горячий

Блок Б холодный

Предположим, мы соединяем эти два блока и изолируем все остальные внешние поверхности. Изоляция предназначена для уменьшения потерь тепла от блока. Вы можете быстро понять, что тепловая энергия будет перетекать от горячего блока к холодному. Передача тепла будет продолжаться до тех пор, пока оба блока не достигнут одинаковой температуры (температурного равновесия).

Это один из способов передачи тепла в обоих блоках. Это кондуктивный режим теплопередачи. Используя уравнение закона теплопроводности, мы можем рассчитать теплопередачу с помощью этого эксперимента. Выполнение в лаборатории теплопередачи (машиностроение и химическая инженерия) очень информативно и важно с практической точки зрения.

Видео:8.1 Решение уравнения теплопроводности на отрезкеСкачать

История закона Фурье

Фурье начал свою работу по выражению теплопроводности в 1822 году. Он также дал понятие ряда Фурье и интеграла Фурье. Он был математиком. Его закон теплопроводности хорошо известен благодаря его имени «закон теплопроводности Фурье».

Видео:Уравнение в частных производных Уравнение теплопроводностиСкачать

Единицы закона Фурье

Для теплопередачи сформулирован закон Фурье теплопроводности. Итак, мы можем рассматривать для него единицу теплоотдачи. Единицей теплоотдачи является ватт (Дж / с) Вт.

Видео:Уравнения математической физики. Одномерное волновое уравнение. Метод Фурье.Скачать

Допущения закона Фурье

Есть некоторые предположения о законе теплопроводности Фурье. Закон применяется только при соблюдении и соблюдении следующих условий.

• Кондуктивная теплопередача будет происходить в стационарных условиях объекта.
• Поток тепла должен быть однонаправленным.
• Температурный градиент должен быть постоянным на протяжении всего процесса, а температурный профиль должен быть линейным.
• Внутреннее тепловыделение должно быть нулевым.
• Ограничивающие поверхности должны быть должным образом изолированы.
• Материал должен быть однородным и изотропным.

Видео:Метод Фурье для волнового уравненияСкачать

Пример закона теплопроводности Фурье

Есть много примеров закона теплопроводности в повседневной жизни. Некоторые примеры обсуждаются ниже.

В кружке горячий кофе. Теперь вы знаете, что тепло будет передаваться с горячей стороны на холодную. Здесь передача тепла происходит от внутренней стенки к внешней стенке кружки. Это кондуктивный перенос тепла, основанный на законе теплопроводности Фурье.

В качестве примера можно рассмотреть стену нашего дома.

Если в стержне происходит внутреннее тепловыделение, тепло будет течь во внутренней части к внешним поверхностям.

Можно потрогать любое электрическое и электронное оборудование. Вы получите немного тепла. Все эти устройства могут быть примером закона Фурье.

Видео:2.1. Метод характеристик. Задача Коши для гиперболического уравнения на плоскости.Скачать

Число Фурье

Это безразмерное число, полученное с помощью безразмерного уравнения теплопроводности..

Число Фурье обозначается F_o

L — длина пластины (диаметр в случае цилиндра) в м.

K — коэффициент градиентного переноса

Видео:4.3 Решение неоднородного волнового уравнения на бесконечной прямойСкачать

Поток закона Фурье

Согласно информации закон теплопроводности,

Тепловой поток можно определить как тепловой поток на единицу площади в единицу времени прямо пропорционален разнице температур между горячей и холодной стороной (температурный градиент).

Видео:Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

Тепловой поток

Тепловой поток можно определить как тепловой поток на единицу площади в единицу времени прямо пропорционален разнице температур между горячей и холодной стороной (температурный градиент).

Видео:Преобразование ФурьеСкачать

Уравнение теплового потока

Уравнение теплового потока приведено ниже.,

q- тепловой поток в Вт / м 2

K — теплопроводность, Вт / м · K

ΔT / ΔX — температурный градиент,

Видео:Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать

Агрегаты теплового потока

Единица теплового потока — Вт / м 2

Видео:6.1 Смешанные краевые задачи для уравнений гиперболического и параболического типов. Метод Фурье.Скачать

Часто задаваемые вопросы

Видео:Неоднородное уравнение колебания струныСкачать

Что такое закон Фурье

«Скорость теплопередачи через материал или образец прямо пропорциональна площади поперечного сечения, через которую проходит тепло, и разности температур вдоль торцевых поверхностей материала».

Мы можем записать это утверждение математически как,

q = скорость теплопередачи в ваттах (Вт или Дж / с)

K = теплопроводность материала или образца (Вт / м · K)

A = Площадь поперечного сечения, через которую проходит тепло, в м 2

dT = разница температур между горячей и холодной сторонами в K (Кельвинах)

dx = Толщина материала в м (толщина между горячей и холодной стороной)

Самое важное: здесь в уравнении отрицательный знак означает, что тепло всегда течет в направлении уменьшения температуры.

Видео:13.1. Что такое ряд Фурье?Скачать

Каковы предположения закона теплопроводности Фурье?

Есть некоторые предположения о законе теплопроводности Фурье. Закон применяется только при соблюдении и соблюдении следующих условий. Закон теплопроводности Фурье можно сравнить с законом охлаждения Ньютона и законом диффузии Фика. Допущения в каждом законе разные.

1. Кондуктивная теплопередача будет происходить в стационарных условиях объекта.
2. Поток тепла должен быть однонаправленным.

1. Температурный градиент не изменится, а температурный профиль должен быть линейным.
2. Внутреннее тепловыделение должно быть нулевым.
3. Ограничивающие поверхности должны быть должным образом изолированы.
4. Материал должен быть однородным и изотропным.

Что является доказательством закона теплопроводности Фурье и отрицательного градиента?

Доказательство закона теплопроводности Фурье уже дано в теме «Закон Фурье».

Отрицательный градиент используется, потому что тепло всегда течет при понижении температуры.

Этот вопрос очень важен для собеседования, потому что интервьюер всегда старается проверить ваши фундаментальные знания.

Чем закон теплопроводности Фурье противоречит теории относительности?

Закон Фурье противоречит теории относительности из-за его мгновенного распространения тепла через диффузию тепла. Если мы рассмотрим зависящую от времени диффузию тепла с помощью уравнения в частных производных, то рост теплового потока будет со временем релаксации. На этот раз порядка 10 -11 . Распространение тепла в природе занимает бесконечное время. Время релаксации незначительно.

Если исключить время релаксации, уравнение станет законом теплопроводности Фурье. Это нарушает популярную теорию Эйнштейна (теория относительности). Скорость света в вакууме составляет 2.998 * 10. 8

Чем физика, лежащая в основе закона Фурье, отличается от физики, лежащей в основе закона охлаждения Ньютона

Как мы уже знаем, закон Фурье используется для теплопроводности, а закон охлаждения Ньютона — для конвективной теплопередачи. Предположим, у вас есть вопрос, почему для анализа скорости теплопередачи требуются два разных закона. Причина в том, что режимы теплопередачи отличаются от индивидуальной физики.

Перенос тепла проводимостью происходит за счет микроскопической диффузии и столкновений молекул или квазичастиц внутри объекта из-за разницы температур. Если мы видим микроскопически, то диффузный и сталкивающийся любой материал включает в себя молекулы, электроны, атомы. Они передают друг другу кинетическую и потенциальную энергию микроскопически. Эта энергия известна как внутренняя энергия объекта. Закон гласит, что теплопроводность является законом Фурье.

Конвекционную теплопередачу в любом объекте можно определить как теплопередачу от одной молекулы к другой за счет перемещения жидкостей или потока жидкости. Закон охлаждения Ньютона определяет конвекционную теплопередачу.

Физика, используемая для отдельного процесса, различна. Следовательно, регулирующий закон для человека отличается.

В чем сходство между законом вязкости Ньютона, законом теплопроводности Фурье и законом диффузии Фика?

Это аналогия между этими уравнениями.

Закон Фурье теплопроводности

В нем описан процесс теплопроводности. Уравнение можно записать следующим образом:

Уравнение теплового потока приведено ниже.,

q- тепловой поток в Вт / м 2

K — теплопроводность, Вт / м · K

ΔT / ΔX — температурный градиент,

Закон диффузии Фика

Он используется для описания и определения процесса массопереноса. Уравнение массопереноса можно записать следующим образом:

(dC / dx) — градиент концентрации

D — коэффициент диффузии транспортных свойств

Закон вязкости Ньютона

Он используется для передачи импульса и широко используется для изучения вязкости любой жидкости.

Здесь (du / dx) — градиент скорости

μ — вязкость жидкости

Таким образом, вы можете сразу проанализировать три разных закона относительности этих уравнений.

Чтобы прочитать больше статей по соответствующей теме, пожалуйста нажмите сюда

Последнее сообщение о машиностроении

Вопрос 31. Теплопроводность. Закон Фурье. Коэффициент теплопроводности.

Теплопроводность — процесс передачи теплоты путем непосредственного соприкосновения тел, имеющих различную температуру. При этом процесс теплообмена происходит за счет передачи энергии микродвижения одних частиц другим.
Тепловой поток , .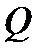

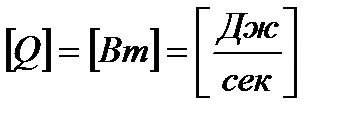
Закон Фурье: тепловой поток пропорционален градиенту температуры и площади, то есть .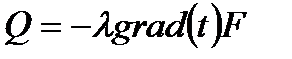
Плотность теплового потока , .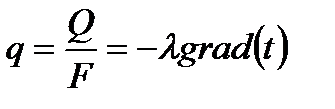
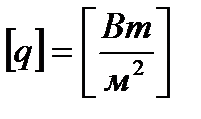
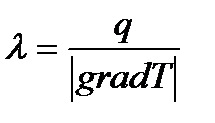
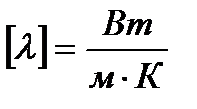
Коэффициент теплопроводности — количество теплоты, которое проходит в единицу времени через единицу поверхности через единичную толщину стенки при перепаде температуры в один градус, .
_____________________________________________________________________

Вопрос 32. Дифференциальное уравнение теплопроводности. Условия однозначности.
Условности:

1. Теплофизические свойства системы: , , .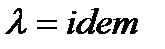

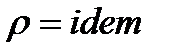
2. Микрочастицы тела неподвижны.

3. Внутренние источники теплоты распределены в теле равномерно.

, где – коэффициент температуропроводности, характеризующий скорость изменения температуры в любой точке тела, [ ]
– теплоемкость тела; – плотность тела; – объемная плотность тепловыделения, [вm/м 3 ]; – температура; – оператор Лапласа.
(для полярных координат , , ),
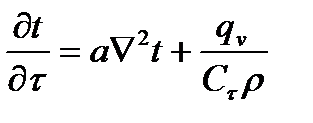
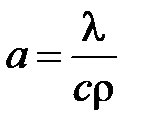
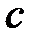
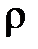
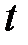
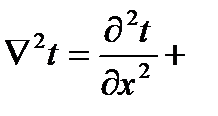
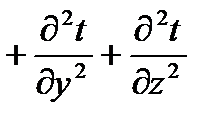
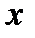
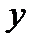
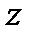
Условия однозначности – математическое описание частных особенностей рассматриваемого процесса.
Решая уравнение 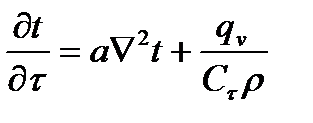, получим общее решение, которое в совокупности с условиями однозначности даст нам частные решения.

Условия однозначности:

1. Геометрические условия (характеризуют форму, размеры и положение тела в пространстве):

a. Форма тела (плоское, цилиндрическое сферическое тело)

b. Ограниченное тело.

c. Неограниченное тело.

2. Физические условия (определяют физические свойства тела и среды)

a. Характер изменения физических параметров:

i. Характер изменения .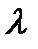

ii. Характер изменения .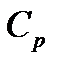

iii. Характер изменения .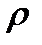

iv. Характер изменения .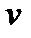

3. Временные условия (дают представление о распределении температуры в исследуемом теле в начальный момент времени):

a. :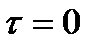

i. .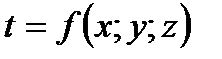

ii. .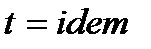

b. .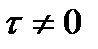

4. Граничные условия (определяют особенности взаимодействия на границе изучаемого тела с окружающими телами (средой)):

a. Граничные условия первого рода – закон изменения температуры на границе тела:

i. .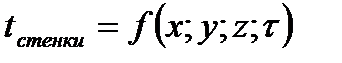

ii. .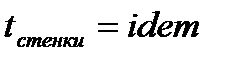

b. Граничные условия второго рода – закон изменения температурного потока в стенке тела:

i. .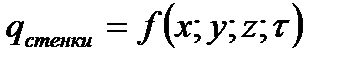

ii. .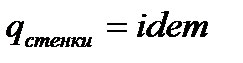

c. Граничные условия третьего рода:

i. Закон изменения температуры окружающей среды.

ii. Закон, по которому идёт теплообмен тела с окружающей средой, .

d. Граничные условия четвёртого рода, .

________________________________________________________

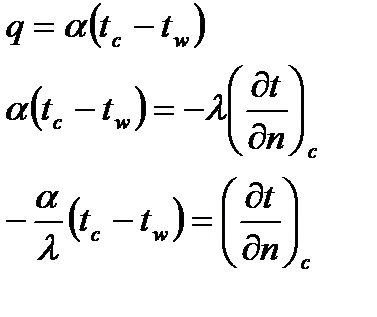
Билет 33. Теплопроводность через однослойные и многослойные плоские стенки.
Теплопроводность – процесс передачи теплоты соприкасающимися, беспорядочно движущимися структурными частицами вещества

В основу теории теплопроводности положен закон Фурье – тепловой поток прямо пропорционален температурному градиенту и площади поверхности тела. Закон Фурье для плоской однослойной стенки

Плотность теплового потока – отношение теплового потока к площади поверхности теплопроводности. Для плоской стенки:
, где .
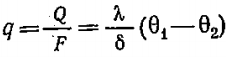
Коэффициент теплопроводности λ характеризует способность тел проводить теплоту.
Плотность теплового потока для стенки, состоящей из n слоёв:
,
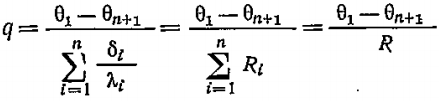
где R – термическое сопротивление многослойной стенки
Многослойную стенку можно заменить эквивалентной однослойной, толщина которой равна толщине многослойной стенки

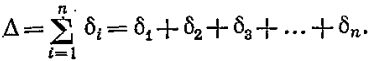
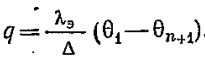
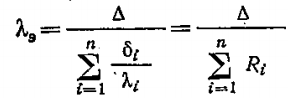
Тогда плотность теплового потока , где
_____________________________________________________________________

Вопрос 34. Теплопроводность через однослойные и многослойные цилиндрические стенки
Тепловой поток для цилиндрической однослойной стенки:

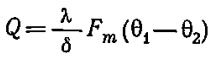
где Fm — расчётная поверхность теплопроводности,

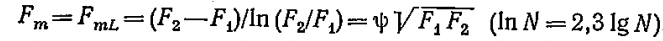
где.
δ – толщина стенки, δ=r₂ – r₁
F₁, F₂ – площади внутренней и наружной поверхностей трубы, [м 2 ]
ψ – коэффициент, характеризующий отношение средней логарифмической F_mL к средней геометрической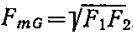
Линейная плотность теплового потока (тепловой поток, отнесённый к единице длины трубы) однослойной стенки определяется по формуле:

Тепловой поток для многослойной цилиндрической стенки:

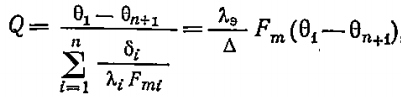
Где

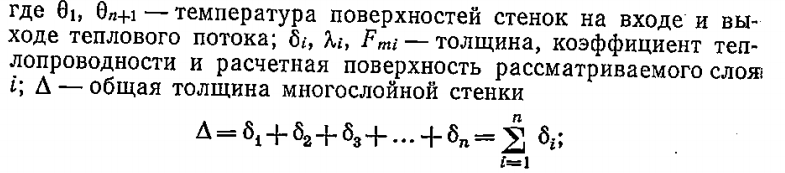
Fm – расчётная поверхность теплопроводности стенки;
λ_э – эквивалентный коэффициент теплопроводности многослойной стенки

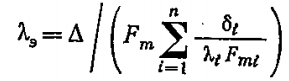
Линейная плотность теплового потока для многослойной стенки трубы

_____________________________________________________________________

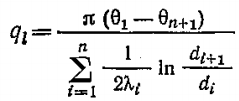
Вопрос 35. Теплоотдача. Уравнение Ньютона. Коэффициент теплоотдачи.
Теплоотдача — конвективный теплообмен между жидкостью и поверхностью твёрдого тела (совместный перенос теплоты конвекцией и теплопроводностью).
Теплоотдачу рассчитывают по формуле Ньютона-Рихмана:

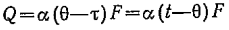
и плотность теплового потока


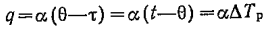
Коэффициент теплоотдачи зависит от: природы возникновения движения жидкости у поверхности теплообмена, режима движения жидкости, физических свойств жидкости, формы, размеров, положения в пространстве и состояния поверхности теплообмена.
____________________________________________________________________

Вопрос 36. Критериальные уравнения, физический смысл критериев подобия.Числа подобия, составленные только из заданных величин математического описания задачи, называются определяющими критериями подобия. Критерии подобия, содержащие альфа, называются определяемыми.
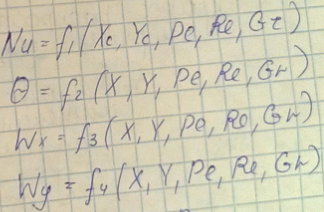
Число Нуссельта, или критерий теплоотдачи, характеризует соотношение тепловых потоков, передаваемых конвекцией и теплопроводностью по нормали через пристенный слой.
, где
— коэффициент теплоотдачи, [Вт/м^2*С]
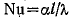
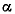
l – определяющий линейный размер, [м]
— коэффициент теплопроводности жидкости, [Вт/м**С]
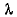
Число Рейнольдса – критерий гидродинамического подобия, характеризуется соотношением сил инерции и молекулярного трения (вязкости)
, где
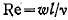
w – средняя (линейная) скорость жидкости, определяется отношением объемного расхода к площади поперечного сечения потока, [м/с],
— кинематическая вязкость жидкости, [м^2/с]
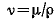
По числовому значению Re судят о режиме течения жидкости:
Re =10^4 – развитый турбулентный
2320 2 К 4 ], ε – степень черноты наружной поверхности опытной трубы, F – площадь наружной поверхности опытной трубы.
Тепловой поток, передаваемый от опытной трубы в окружающую среду путем конвекции, равен

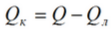
а опытное значение коэффициента теплоотдачи составляет

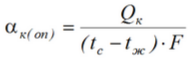
Определив при средней температуре пограничного слоя tm теплофизические свойства сухого воздуха λ; ν; β; Pr (находятся значения числа Грасгофа)
и комплекса (GrPr).
В зависимости от значения комплекса (GrPr) подбирается коэффициент C и показатель степени n в уравнении подобия конвективного теплообмена и определяются число Нуссельта

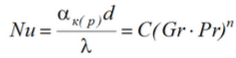
и расчетное значение коэффициента теплоотдачи

_____________________________________________________________________

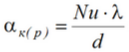
Вопрос 38. Последовательность расчетов конвективного теплообмена в условиях вынужденной конвекции.
Рассчитаем конвективный теплообмен на примере лабораторной работы

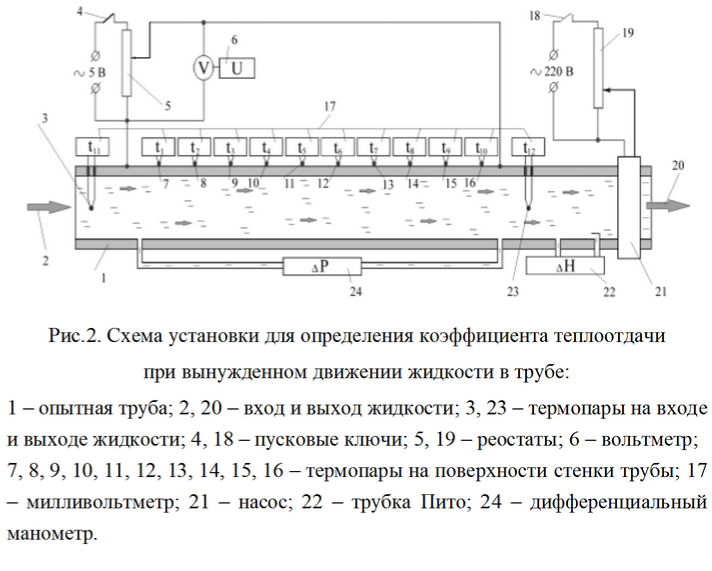
Дано: напряжение U [В]
Динамический напор жидкости ΔH [кГ/м 2 ]
Температура стенки трубы t₁ [°С] (10 измерений)
Температура жидкости на входе в трубу t₁₁ [°C]
Температура жидкости на выходе из трубы t₁₂ [°С]
Рассчитаем коэффициент теплоотдачи
Обработка опытных данных начинается с определения средней темпе-ратуры поверхности стенки трубы tс:

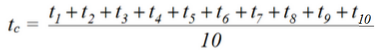
Средняя температура потока воды в трубе:

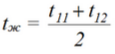
При средней температуре потока по таблице определяются теплофизические свойства воды: ρ; с_p; λ; v.
Число Прандтля при средней температуре потока (10):

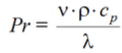
Скорость движения воды в трубе:

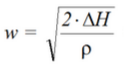
При движении жидкость нагревается на:

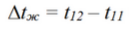
Количество теплоты в единицу времени, которое получает поток жид-кости от горячей поверхности стенки трубы:

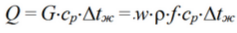
Плотность теплового потока от стенки трубы к потоку жидкости:

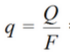
Опытное значение среднего коэффициента теплоотдачи:

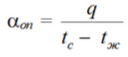
Число Рейнольдса (8) для потока жидкости в трубе:

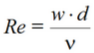
В зависимости от полученного значения определяется выражение для поиска числу Нуссельта.
Теоретическое значение среднего коэффициента теплоотдачи вычисляется из определения критерия Нуссельта

_____________________________________________________________________
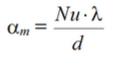