Какое еще уравнение равновесия надо составить чтобы убедиться что система сил уравновешена (8 видео)

Условия равновесия плоской системы сил

В соответствии с первой аксиомой статики тело будет находиться в равновесии, если действующая на него система сил взаимно уравновешивается (эквивалентна нулю).

Плоская система сил может быть приведена к главному вектору и главному моменту и, соответственно, будет в равновесии, если главный вектор равен нулю и главный момент относительно любой точки тела равен нулю.

В случае равенства нулю главного вектора его проекции на координатные оси F_TSI—_с, F_TSly также равны нулю. Следовательно, уравнения равновесия плоской системы сил можно записать как:

или в упрощенной форме уравнения равновесия плоской системы сил запишем в виде:

Уравнения равновесия (4.2, 4.3) называют основными уравнениями равновесия.

Система сил, лежащих в одной плоскости, считается уравновешенной, если алгебраические суммы проекций всех сил на координатные оси равны нулю и равна нулю алгебраическая сумма моментов всех сил системы относительно любой точки.

В некоторых случаях удобней пользоваться уравнениями равновесия, содержащими два уравнения, устанавливающих равенство нулю всех моментов относительно двух различных точек, и одного уравнения, определяющего равенство нулю проекций всех сил на ось

ось х в этом случае не должна лежать перпендикулярно линии, соединяющей точки АВ. При использовании системы уравнений (4.4) уравнение, определяющее равенство нулю проекций всех сил ось у, = 0? применяется как дополнительное, позволяющее выполнять проверку расчетов.

В случае расчетов по уравнениям (4.3) в качестве дополнительного уравнения для проверки расчетов применяют уравнение о равенстве нулю суммы моментов относительно второй точки, взятой на теле 0.

Может применяться и третья форма уравнений равновесия, устанавливающая равенство нулю суммы моментов всех сил системы относительно любых трех точек, не лежащих на одной прямой

в качестве дополнительных уравнений, по которым можно выполнять проверку расчетов в этом случае, применяют уравнения:

Для обеспечения равновесия тела необходимо не менее трех связей. Решение системы трех уравнений статики позволяет определить три реакции в связях.

Частным случаем плоской системы сил является система параллельных сил. Равновесие системы параллельных сил рассматривается в параграфе 6.2.

Содержание

iSopromat.ru
Формы условий равновесия
Первая форма
Вторая форма
Третья форма
Другие условия равновесия
Презентация к защите
📹 Видео

Видео:Термех. Статика. Равновесие плоской произвольной системы силСкачать

iSopromat.ru

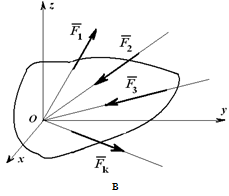
Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия для систем параллельных и сходящихся сил:

Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.

Если система уравновешена, то получаем условия равновесия: R=0, M_O=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:

Видео:Статика. Условия равновесия плоской системы сил (23)Скачать

Формы условий равновесия

Первая форма

Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:

причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия.

Вторая форма

Уравнения равновесия могут быть записаны иначе:

Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.

Третья форма

Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.

Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.

Видео:Статика. Момент сил. Условия равновесия тел | Физика ЕГЭ, ЦТ, ЦЭ | Физика для школьниковСкачать

Другие условия равновесия

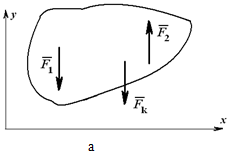
При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):

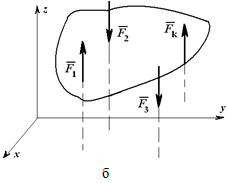
Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:

Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:

и два уравнения для плоской системы:

В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Система сходящихся сил. Решение задач по МещерскомуСкачать

Презентация к защите

Условие равновесия произвольной плоской системы сил может быть сформулировано следующим образом:

Для того чтобы твердое тело под действием произвольной плоской системы сил находилось в равновесии, необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил системы на любую ось равнялась нулю и алгебраическая сумма моментов всех сил системы относительно любой точки в плоскости действия сил равнялась нулю.

Получим основную форму уравнения равновесия:

Теоретически уравнений моментов можно записать бесконечное множество, но практически доказано, что на плоскости можно составить только три независимых уравнения моментов и при этом три точки (центры моментов) не должны лежать на одной линии.

Методы изготовления эвольвентных зубчатых колес. Существует множество вариантов изготовления зубчатых колес. В их основу положены два принципиально отличных метода: метод копирования, при котором рабочие кромки инструмента по форме соответствуют обрабатываемой поверхности ( конгруентны ей, т. е. заполняют эту поверхность как отливка заполняет форму ); метод огибания, при котором инструмент и заготовка за счет кинематической цепи станка выполняют два движения — резания и огибания (под огибанием понимается такое относительное движение заготовки и инструмента , которое соответствует станочному зацеплению, т. е. зацеплению инструмента и заготовки с требуемым законом изменения передаточного отношения).

Практически для решения задач на плоскости достаточно трех уравнений равновесия. В каждом конкретном случае используются уравнения с одним неизвестным.

Для разных случаев используются три группы уравнений равновесия.