Каким методом математически можно решать систему уравнений составленную по законам кирхгофа

Видео:Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Метод уравнений Кирхгофа

Если электрическая цепь с помощью эквивалентных преобразований не сводится к одноконтурной цепи, то для ее расчета используются специальные методы: уравнений Кирхгофа, контурных токов, наложения, узловых потенциалов, эквивалентного генератора. Рассмотрим их.

Самым общим методом расчета электрических цепей является метод уравнении Кирхгофа. Суть его заключается в составлении системы уравнений в соответствии с первым и вторым законами Кирхгофа и решении этой системы относительно неизвестных токов. Система уравнений разрешима, если все входящие в нее уравнения являются линейно независимыми и число уравнений в системе равно числу неизвестных величин. Например, если электрическая цепь имеет у узлов и Ь ветвей, а следовательно, и Ь неизвестных токов, то необходимо составить и решить систему Ь линейно независимых уравнений. Покажем, что эти уравнения можно составить по первому и второму законам Кирхгофа.

По первому закону Кирхгофа можно составить столько уравнений, сколько узлов имеет электрическая цепь, т.е. у уравнений. Однако линейно независимыми будут только у — 1 уравнения. Покажем это на примере.

Составим уравнения по первому закону Кирхгофа для электрической схемы, у которой четыре узла и шесть ветвей (рис. 2.19).

Произвольно выберем направления токов в ветвях; тогда для первого узла / — К — 4 = 0, для второго К + А — /3 = 0, для третьего /₆ + /₃ — /₄ = 0, для четвертого /₄ — /| — /₅ = 0. Сложив первые три уравнения, получим — /₄ + /| + /₅ = 0. Умножим это уравнение на — 1. Тогда уравнение для четвертого узла можно получить линейными комбинациями из уравнений, составленных по первому закону Кирхгофа для первых у — 1 узлов.

Видно, что одно из уравнений системы, составленное по числу узлов, является зависимым. Поэтому по первому закону Кирхгофа составляется только у — 1 уравнение, т.е. на одно меньше, чем число узлов в электрической цепи. Так как в схеме четыре узла, то число уравнений, которые составляются по первому закону Кирхгофа, равно трем. Остальные п = Ь — (у — 1) линейно независимых уравнений составляются по второму закону Кирхгофа. Для рассматриваемой схемы п = 6 — (4 — 1) = 3.

Таким образом, для электрической цепи, содержащей у узлов и Ь ветвей, по второму закону Кирхгофа можно составить п = Ь — (у — 1) линейно независимых уравнений. При этом общее число уравнений, составленных по первому и второму законам Кирхгофа, будет равно числу ветвей электрической цепи.

Расчет электрических цепей с помощью законов Кирхгофа целесообразно проводить в следующем порядке.

• 1. Определить число узлов у и число ветвей Ь в электрической цепи. В соответствии с этим найти количество уравнений, которые необходимо составить по первому и второму законам Кирхгофа.
• 2. Обозначить на схеме цепи токи в ветвях и произвольно выбрать их направления. Выбрать независимые замкнутые контуры электрической цепи таким образом, чтобы в каждый контур, во-первых, входило возможно меньшее число ветвей и, во-вторых, чтобы в каждый последующий контур входила хотя бы одна новая ветвь. Произвольно задаться направлением обхода контуров.
• 3. Составить)’ — 1 уравнение по первому закону Кирхгофа. При этом считать положительными токи, входящие в узел, а отрицательными — выходящие из узла, или наоборот.
• 4. Составить п = Ь — (у — 1) уравнений по второму закону Кирхгофа. В этих уравнениях значение ЭДС берется со знаком «+», если направление ЭДС совпадает с направлением обхода контура. Падения напряжений на сопротивлениях в замкнутом контуре электрической цепи берутся со знаком «+», если направление обхода контура совпадает с выбранным направлением тока, и со знаком «-», если не совпадает.

• 5. Решить составленную систему уравнений относительно неизвестных токов. Если при этом некоторые токи получаются отрицательными, это означает, что их действительные направления противоположны произвольно выбранным. Направления этих токов на схеме обратные.
• 6. Проверить правильность решения задачи путем составления уравнения баланса мощности.

Пример 2.4. В электрической цепи (рис. 2.20) Е =50 В, ?3 = 10 В, Гц = 0,4 Ом, г,2 = 1 Ом, /*| = 3 Ом, /’2 = г у = 2 Ом. Требуется определить токи в ветвях.

Решение. В схеме два узла и три ветви. Следовательно, по первому закону Кирхгофа необходимо составить одно уравнение, а по второму — два. Обозначим на схеме электрической цепи узлы, токи в ветвях и стрелками произвольно укажем их положительные направления. Выберем два независимых контура и стрелками покажем направления их обхода. Составим уравнение по первому закону Кирхгофа для первого узла: /₍ + Л, — /₃ = 0 .

Составим уравнения по второму закону Кирхгофа для выбранных независимых контуров:

Полученные уравнения образуют систему независимых уравнений с тремя неизвестными:

Решив эту систему, будем иметь: 1 = 10 А, /₂ = —2А, /₃ = 8 А. По полученным знакам токов устанавливаем, что действительные направления токов 1 и /3 совпадают, а тока /₂ — противоположно произвольно выбранным положительным направлениям.

Правильность расчета токов проверяют по балансу мощностей.

При расчете электрических цепей с помощью законов Кирхгофа источники электрической энергии, заданные в виде источника тока, должны учитываться при составлении уравнений по первому закону Кирхгофа.

Недостатком рассмотренного метода расчета электрических цепей является его громоздкость (число уравнений равно числу ветвей).

Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Правила (законы) Кирхгофа простыми словами

На практике часто встречаются задачи по расчётам параметров токов и напряжений в различных разветвлённых цепях. В качестве инструмента для расчётов используют правила Кирхгофа (в некоторой литературе их называют еще законами, хотя это не совсем корректно) – одни из фундаментальных правил, которые совместно с законами Ома позволяет определять параметры независимых контуров в самых сложных цепях.

Учёный Густав Киргхоф сформулировал два правила [1], для понимания которых введено понятие узла, ветви, контура. В нашей ситуации ветвью будем называть участок, по которому протекает один и тот же ток. Точки соединения ветвей образуют узлы. Ветви вместе с узлами образуют контуры – замкнутые пути, по которым течёт ток.

Видео:Как составить уравнения по законам Кирхгофа?Скачать

Первое правило Кирхгофа

Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.

Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.

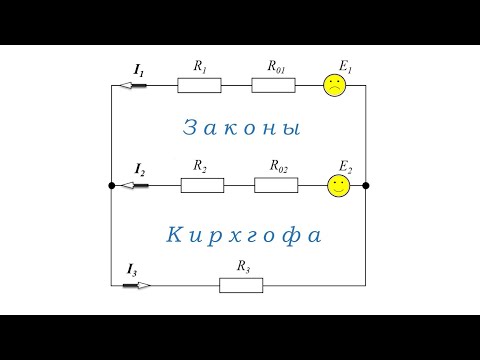
На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.

Рис. 1. Схема контура

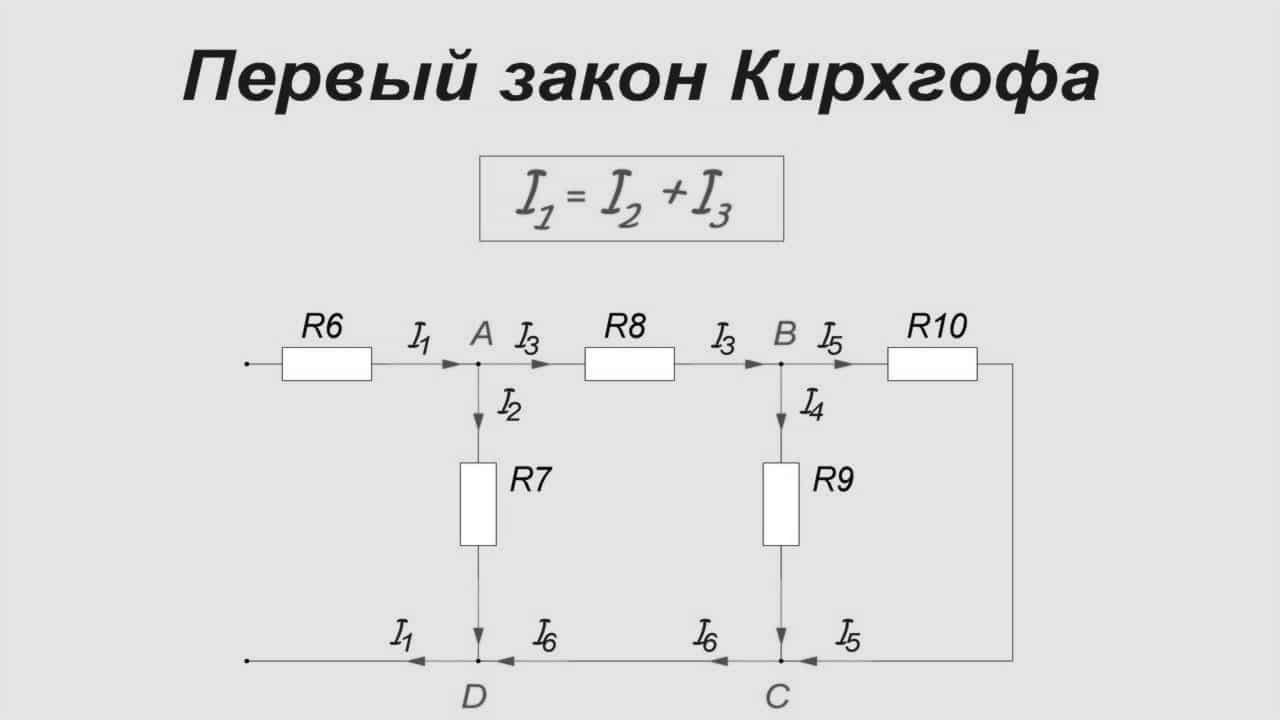
Ток I₁ входит в узел A, образованный ветвями контура. На схеме электрический заряд распределяется в двух направлениях – по ветвям AB и AD. Согласно правилу Кирхгофа, входящий ток равен сумме выходящих: I₁ = I₂ + I₃.

На рисунке 2 представлен абстрактный узел, по ветвям которого течёт ток в разных направлениях. Если сложить векторы i₁, i₂, i₃, i₄ то, согласно первому правилу Кирхгофа, векторная сумма будет равняться 0: i₁ + i₂ + i₃ + i₄ = 0. Ветвей может быть сколько угодно много, но равенство всегда будет справедливым, с учётом направления векторов.

Запишем наши выводы в алгебраической форме, для общего случая:

Для использования этой формулы, требуется учитывать знаки. Для этого необходимо выбрать направление одного из векторов тока (не важно, какого) и обозначить его знаком «плюс». При этом знаки всех других величин определить, исходя от их направления, по отношению к выбранному вектору.

Чтобы избежать путаницы, ток, направленный в точку узла, принято считать положительным, а векторы, направленные от узла – отрицательными.

Изложим первое правило Кирхгофа, выраженное приведённой выше формулой: «Алгебраическая сумма сходящихся в определённом узле токов, равна нулю, если считать входящие токи положительными, а отходящими – отрицательными».

Первое правило дополняет второе правило, сформулированное Кирхгофом. Перейдём к его рассмотрению.

Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Второе правило Киргхофа

Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.

Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.

При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.

Рис. 4. Иллюстрация второго правила Кирхгофа

Формулы, которые изображены на рисунке применяются в частных случаях для вычисления параметров простых схем.

Формулировки уравнений общего характера:

, где где L_k и C_k – это индуктивности и ёмкости, соответственно.

Линейные уравнения справедливы как для линейных, так и для нелинейных линеаризованных цепей. Они применяются при любом характере временных изменений токов и напряжений, для разных источников ЭДС. При этом законы Кирхгофа справедливы и для магнитных цепей. Это позволяет выполнять вычисления для поиска соответствующие параметров.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Закон Кирхгофа для магнитной цепи

Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.

То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.

Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).

Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.

Примечание: Составляя уравнения с использованием формул, вытекающих из правил Кирхгофа, надо прежде определиться с положительным направлением потоков, функционирующих в ветвях, сопоставив их с направлением обходов существующих контуров.

При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».

Видео:решение задачи составлением уравнений по правилам киргофа. Законы киргофа кратко на практикеСкачать

Примеры расчета цепей

Рассмотрим ещё раз рисунок 3. На нём изображено 4 разнонаправленных вектора: i₁, i₂, i₃, i₄. Из них – два входящие ( i₂, i₃) и два исходящие из узла (i₁, i₄). Положительными будем считать те векторы, которые направлены в точку соединения ветвей, а остальные – отрицательными.

Тогда, по формуле Кирхгофа, составим уравнение и запишем его в следующем виде: – i₁ + i₂ + i₃ – i₄ = 0.

На практике такие узлы являются частью контуров, обходя которые можно составить ещё несколько линейных уравнений с этими же неизвестными. Количество уравнений всегда достаточно для решения задачи.

Рассмотрим алгоритм решения на примере рис. 5.

Рис. 5. Пример для расчёта

Схема содержит 3 ветви и два узла, которые образуют три пары по два независимых контура:

Запишем независимое уравнение, выполняющееся, например, в точке а. Из первого правила Кирхгофа вытекает: I₁ + I₂ – I₃ = 0.

Воспользуемся вторым правилом Кирхгофа. Для составления уравнений можно выбрать любой из контуров, но нам необходимы контуры с узлом а, так как для него мы уже составили уравнение. Это будут контуры 1 и 2.

Пишем уравнения:

Решаем систему уравнений:

Так как значения R и E известны (см. рисунок 5), мы придём к системе уравнений:

Решая эту систему, получим:

Потенциал узла а равен: U_a = I₃*R₃ = 3,55 × 3 = 10,65 В. Чтобы убедиться в верности наших расчётов, проверим выполнение второго правила по отношению к контуру 3:

E₁ – E₂ + I₁R₁+ I₂R₂ = 12 – 15 + 1,36 – 4,38 = – 0,02 ≈ 0 (с учётом погрешностей, связанных с округлениями чисел при вычислениях).

Если проверка выполнения второго правила успешно завершена, то расчёты сделаны правильно, а полученные данные являются достоверными.

Применяя правила (законы) Кирхгофа можно вычислять параметры электрической энергии для магнитных цепей.

Видео:Применение законов Кирхгофа при решении задачСкачать

Первый и второй законы Кирхгофа

Некоторые электрические цепи можно изобразить в виде простого контура, содержащего источник питания и небольшое количество деталей — резисторов, конденсаторов или других. Но существуют и большие схемы, включающие в себя несколько замкнутых ветвей. В этих случаях важно точно рассчитать электрические параметры на любом рассматриваемом участке. Законы Кирхгофа позволяют их определить путём составления и решения нескольких простых уравнений.

Видео:Законы Кирхгофа. Метод контурных уравненийСкачать

Первый закон Кирхгофа

Закон Ома описывает взаимосвязь между напряжением, сопротивлением и силой тока в простых одноконтурных цепях. На практике чаще встречаются сложные разветвленные цепи, состоящие из нескольких контуров и многих узлов, которые невозможно описать, применяя стандартные правила для расчета последовательных и параллельных цепей.

Определить напряжение и силу тока в разветвленных цепях позволяют правила Кирхгофа, которые в технической литературе обычно называют законами Кирхгофа. Хотя более корректным следует считать название «правила», поскольку они не являются фундаментальными законами природы. Например, первое правило Кирхгофа вытекает из закона сохранения заряда. Оно гласит, что сумма всех токов в каждом узле электроцепи равна нулю.

Формулировка закона требует уточнения следующих терминов:

• Узел — это определённое место на схеме, в котором сходится 3 или большее количество проводов. Узлами можно назвать точки, расположенные на протяжении 1 провода, если в этих местах подсоединены ещё провода.
• Движение тока, направленного к определённому узлу, условно называют положительным, противоположное — отрицательным.

Закон Кирхгофа, если говорить простыми словами, может быть сформулирован так: сколько токов втекает в узел, столько же и вытекает. Это свидетельствует о непрерывности тока для электрической цепи. Поэтому существует ещё одна формула, выражающая первое правило Кирхгофа:

Здесь с одной стороны знака равенства рассматриваются токи, входящие в определённый узел, а с другой — выходящие.

При использовании первого закона Кирхгофа для цепи переменного тока применяются мгновенные значения напряжений, которые принято обозначать буквой İ. Расчеты в этом случае проводятся по уравнению, представленному в комплексной форме.

Видео:2 8 Метод непосредственного применения законов КирхгофаСкачать

Второй закон Кирхгофа

Когда рассматривается электрическая цепь, подключённая к источнику тока, в каждой её точке имеется определённый потенциал. Разность между ними создаёт электрическое поле, которое вызывает перемещение зарядов.

Цепь представляет собой замкнутый контур, по которому движутся электроны. Электрическое поле выполняет определённую работу по их перемещению. Каждый заряд перемещается по цепи, а затем под действием ЭДС источника замыкает круг.

Второй закон Кирхгофа гласит, что работа по перемещению заряда вдоль любого контура электроцепи с возвратом в начальную точку равна нулю. В этой формулировке подразумевается любой замкнутый контур, причем как тот, который включает источник питания, так и о тот, где его нет.

Работа электрического поля при перемещении заряда в рассматриваемом случае представляет собой сумму падений напряжения для каждого из участков контура. Таким образом, второе правило или закон Кирхгофа гласит, что сумма напряжений всех ветвей в контуре равняется нулю. Это можно выразить в виде следующего уравнения:

Если напряжение и направление обхода контура совпадают, то U записывают со знаком плюс, в противном случае — со знаком минус. Направление обхода выбранного контура может быть определено произвольным образом. Второе правило Густава Кирхгофа его не регламентирует.

Если в контуре есть один или несколько источников питания, то формулу можно выразить следующим образом:

Здесь имеется p источников питания, q участков контура. Сумма всех ЭДС имеющихся источников питания равна сумме падений напряжения.

Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Значение правил Кирхгофа

Законы Кирхгофа выражают фундаментальные принципы физики. Их формулировки кажутся очень простыми и очевидными. Но на самом деле они представляют собой метод, позволяющий рассчитать электрические параметры сетей очень сложной конфигурации.

С помощью законов Кирхгофа можно составить систему независимых уравнений для расчета параметров электрической цепи. Важно, чтобы их количество было не меньше, чем число параметров, которые необходимо определить.

На приведённом рисунке представлена электроцепь, для которой будет проводиться расчёт. Используя первый закон или правило Кирхгофа, для узла A можно записать:

В этот узел входят два тока, а выходит один. Далее необходимо применить второе правило. Для этого можно выбрать внешний контур. Видно, что здесь имеется два источника тока и два резистора. Поэтому будут получены уравнения:

Здесь приведены 2 эквивалентные формулы. В левой части равенства учтены электродвижущие силы двух источников тока, в правой — падение напряжения на обоих резисторах с учётом направления токов. Ещё одно уравнение можно получить из 2 закона при обходе по правому внутреннему контуру:

В результате получена система, включающая в себя три уравнения с тремя неизвестными:

Используя конкретные данные, можно подставить в систему уравнений численные значения и найти, чему равна сила тока для каждой ветви, относящейся к узлу A. При расчётах важно понимать, что при достаточно сложной конфигурации электроцепи иногда бывает непросто определить направление силы тока для каждой ветви.

Первый и второй законы Густава Кирхгофа позволяют точно определить не только величину тока, но и его знак. Если в приведённом примере после вычисления искомых значений с помощью представленной системы уравнений окажется, что ток с индексом 2 принимает отрицательное значение, то это означает, что на самом деле он имеет направление, противоположное указанному на рисунке.

Видео:Как решать систему уравнений графическим методом? | Математика | TutorOnlineСкачать

Законы для магнитного поля

Правила Кирхгофа нашли свое применение и при расчете магнитных цепей. Первый закон Кирхгофа для магнитной цепи выглядит так:

Проще говоря, сумма всех магнитных потоков, проходящих через узел, равняется нулю.

Второй закон в применении к магнитным полям звучит следующим образом: «Сумма магнитодвижущих сил в контуре равняется сумме магнитных напряжений». Формула выглядит так:

Кирхгофом выведены правила, имеющие абсолютный прикладной характер. С их помощью можно решать практические вопросы в электротехнике. Широкое применение этих правил объясняется простотой формулировки уравнений и возможностью их решения с применением стандартных способов линейной алгебры.

Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Видео по теме

🔥 Видео

Система уравнений. Метод алгебраического сложенияСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Решение систем уравнений методом подстановкиСкачать

Законы Кирхгофа - самое простое и понятное объяснение этих законовСкачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать

СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать