Какие из перечисленных методов служат для решения уравнений с одним неизвестным

Общие сведения о численном решении уравнений с одним неизвестным

Пусть задана непрерывная функция f(x). Требуется найти корни уравнения f(x) = 0 численными методами – это и является постановкой задачи. Численное решение уравнения распадается на несколько подзадач:

1. Анализ количества, характера и расположения корней (обычно путем построения графика функции или исходя из физического смысла исследуемой модели). Здесь возможны следующие варианты:
   • единственный корень;
   • бесконечное множество решений;
   • корней нет;
   • имеется несколько решений, как действительных, так и мнимых (например, для полинома степени n). Корни четной кратности выявить сложно.
2. Локализация корней (разбиение на интервалы) и выбор начального приближения к каждому корню. В простейшем случае можно протабулировать функцию с заданным шагом.

Если в двух соседних узлах функция будет иметь разные знаки, то между этими узлами лежит нечетное число корней уравнения (по меньшей мере один).

Метод дихотомии (бисекций)

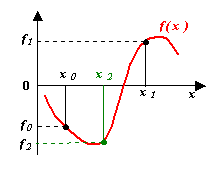
Иначе называется методом половинного деления. Пусть задан начальный интервал [x₀, x₁], на котором f(x₀)f(x₁) ≤ 0 (т.е. внутри имеется не менее чем один корень). Найдем x₂ = ½ (x₀ + x₁) и вычислим f(x₂). Если f(x₀)f(x₂) ≤ 0, используем для дальнейшего деления отрезок [x₀, x₂], если > 0 – используем для дальнейшего деления отрезок [x₁, x₂], и продолжаем деление пополам.

Итерации продолжаются, пока длина отрезка не станет меньше 2ξ – заданной точности. Тогда середина последнего отрезка даст значение корня с требуемой точностью. В качестве иного критерия можно взять
| f(x)| ≤ ξ_y.

Скорость сходимости метода невелика, однако он прост и надежен. Метод неприменим к корням четной кратности. Если на отрезке несколько корней, то заранее неизвестно, к какому из них сойдется процесс.

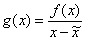
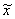
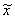
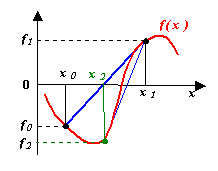
Если на заданном интервале предполагается несколько корней, то существует возможность последовательно исключать найденные корни из рассмотрения. Для этого воспользуемся вспомогательной функцией , где – только что найденный корень. Для функций f(x) и g(x) совпадают все корни, за исключением (в этой точке полюс функции g(x)). Для достижения требуемой точности рекомендуется грубо приблизиться к корню по функции g(x), а затем уточнить его, используя f(x).

Идея метода проиллюстрирована рисунком. Задается интервал [ x₀, x₁], на котором f(x₀)f(x₁) ≤ 0, между точками x₀ и x₁ строится хорда, стягивающая f(x). Очередное приближение берется в точке x₂, где хорда пересекает ось абсцисс. В качестве нового интервала для продолжения итерационного процесса выбирается тот, на концах которого функция имеет разные знаки. Условия выхода из итерационного цикла: 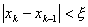или | f(x)| ≤ ξ_y.

Для вывода итерационной формулы процесса найдем точку пересечения хорды (описываемой уравнением прямой) с осью абсцисс: ax₂ + b = 0, где 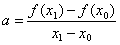; b = f(x₀) — ax₀.

Отсюда легко выразить .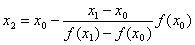

Метод хорд в большинстве случаев работает быстрее, чем метод дихотомии. Недостатки метода те же, что и в предыдущем случае.

Метод Ньютона (касательных.

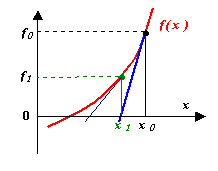
Пусть x₀ – начальное приближение к корню, а f(x) имеет непрерывную производную. Следующее приближение к корню найдем в точке x₁, где касательная к функции f(x), проведенная из точки (x₀, f₀), пересекает ось абсцисс. Затем точно так же обрабатываем точку(x₁, f₁), организуя итерационный процесс. Выход из итерационного процесса по условию .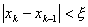

Уравнение касательной, проведенной из точки (x₀, f₀): y(x) = f / (x₀)(x-x₀) + f(x₀) дает для y ( x ₁) = 0 следующее выражение:

, (1)

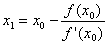
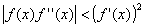
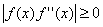
которое и используется для организации итерационного процесса. Итерации сходятся, только если всюду выполняется условие ; в противном случае сходимость будет не при любом начальном приближении, а только в некоторой окрестности корня. Итерации будут сходиться к корню с той стороны, с которой .

Метод обладает самой высокой скоростью сходимости: погрешность очередного приближения примерно равна квадрату погрешности предыдущего приближения. Метод можно использовать для уточнения корней в области комплексных чисел, что необходимо при решении многих прикладных задач, например при численном моделировании электромагнитных колебательных и волновых процессов с учетом временной и пространственной диссипации энергии.

Недостатком метода можно указать необходимость знать явный вид первой и второй производных, так как их численный расчет приведет к уменьшению скорости сходимости метода. Иногда, ради упрощения расчетов, используют т.н. модифицированный метод Ньютона, в котором значениеf / (x) вычисляется только в точке x₀, при этом число итераций увеличивается, но расчеты на каждой итерации упрощаются.

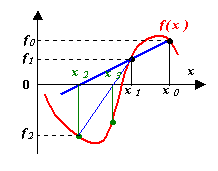
В отличие от метода Ньютона, можно заменить производную первой разделенной разностью, найденной по двум последним итерациям, т.е. заменить касательную секущей. При этом первый шаг итерационного процесса запишется так:

.

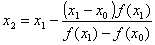
Для начала итерационного процесса необходимо задать x₀ и x₁, которые не обязательно ограничивают интервал, на котором функция должна менять знак; это могут быть любые две точки на кривой. Выход из итерационного процесса по условию .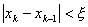

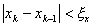
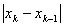
Сходимость может быть немонотонной даже вблизи корня. При этом вблизи корня может происходить потеря точности, т.н. «разболтка решения», особенно значительная в случае кратных корней. От разболтки страхуются приемом Гарвика: выбирают некоторое ξ_x и ведут итерации до выполнения условия . Затем продолжают расчет, пока убывает. Первое же возрастание может свидетельствовать о начале разболтки, а значит, расчет следует прекратить, а последнюю итерацию не использовать.

Метод простых итераций.

Суть метода простых итераций в принципе совпадает с методом, изложенным для решения систем линейных алгебраических уравнений. Для нелинейного уравнения метод основан на переходе от уравнения

К эквивалентному уравнению x = φ(x). Этот переход можно осуществить разными способами, в зависимости от вида f(x). Например, можно положить

где b = const, при этом корни исходного уравнения (2) не изменятся.

Если известно начальное приближение к корню x₀, то новое приближение x₁ = φx(₀), т.е. общая схема итерационного процесса:

Наиболее простой критерий окончания процесса .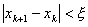

Критерий сходимости метода простых итераций: если вблизи корня |φ / (x)| / (x)| = 0. При этом, исходя из (3), b = –1/f / (x), и итерационная формула (4) переходит в

,

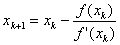
т.е. в формулу метода Ньютона (1). Таким образом, метод Ньютона является частным случаем метода простых итераций, обеспечивающим самую высокую скорость сходимости из всех возможных вариантов выбора функции φ(x).

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Методы решения уравнений с одним неизвестным

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Учитель: Ли Галина Валентиновна

Предмет: алгебра и начала анализа 11 класс

УМК – Математика: — Алгебра и начала математического анализа. 11 класс: учебник для общеобразовательных организаций: базовый и углубленный уровни /Ю.М. Колягин, М.В. Ткачева, Н.Е. Федоров, М.И. Шабунин. – М. Просвещение, 2016

Тема урока: «Методы решения уравнений с одним неизвестным»

предметные: изучить, систематизировать и закрепить теоретические знания по данной теме и научить применять их при решении задач;

личностные : вызвать желание применить приобретенные знания и умения, формировать способность к взаимооценке. самооценке на основе критерия успешной деятельности

метапредметные : совершенствовать навыки самостоятельной работы, формировать умение работать в парах, группе, планировать свои действия в соответствии с поставленной задачей.

Тип урока : урок обобщения знаний

Технологии, используемые на уроке:

Технология развития критического мышления

Технология проблемного обучения

Актуализация знаний, постановка проблемы

Задание 1. Разбейте следующие уравнения на группы по каким-либо признакам (как можно большим количеством способов).

4. 2 x 2 -13 x +15=0 5.

6. cos 7. -5 x = 3 8. =11

9. 3 x 2 +4 x — 207 = 0 10. 9 x -24 = 729 11. log ₅ (2 x +8) = -1

Задание 2. Как бы вы сформулировали тему урока?

Уравнения можно разбить по следующим критериям:

По виду уравнения разбить на 7 групп: линейное, квадратное, показательное, логарифмическое, иррациональное, тригонометрическое, комбинированное

На две группы: алгебраические уравнения и неалгебраические.

По методу решения.

После обсуждения учащиеся приходят к выводу, что новым будет понятие общих методов решения.

Поиск путей решения проблемы, ее решение

Класс делится на группы (по 5 учащихся в каждой). Каждой группе выдаются тексты различного содержания, 5 различных уравнений. Каждый учащийся работает со своим текстом, решает свое уравнение.

Уравнения №1 – метод перехода от уравнения f ( k ( x )) = f ( g ( x )) к уравнению k ( x ) = g ( x )

Уравнения №2 – на метод замены переменной

Уравнение №3 – метод разложения на множители

Уравнение №4 – функционально-графический метод

Уравнение №5 – однородные уравнения

Учитель проверяет ответы учащихся в группе.

2) 2 log ₂ 2 x -3 log ₂ x -1=0

1) log ₇ ( x + 6) = log ₇ ( x 2 — 5 x -10)

2) 25 x -3∙5 x +10=0

3) 3 х х – 3 х+1 + 27 = 9х

2) tg 2 x + tgx -2=0

5) -3 lgx ∙ lg (2 x -1)+2 = 0

1) + 2 x + + 2 x = 1

Какие методы решения уравнений можно выделить как общие?

Каждому учащемуся в группе нужно:

Изучить соответствующую теорию по учебнику (текст №1-стр 165, текст №2-стр.260, текст №3-стр.259, текст №4-стр.265, текст №5)

Решить соответствующее уравнение (уравнение №1, уравнение №2, уравнение №3, уравнение №4, уравнение №5)

По окончании работы учащиеся переходят в новые группы-группы экспертов

Работа в новой группе (все члены группы работали над одной темой). Происходит обмен результатами своей работы, готовится общая презентация: краткое решение каждого уравнения ( основные этапы, ответ), определение выступающего (называет вид уравнения , метод решения).

Взаимооценка (максимальный балл- 3)

Презентации размещаются на доске.

Взаимооценка: каждая группа выставляет баллы другим группам за презентацию

(баллы от 1 до 3). Выявляется группа – победитель.

Метод разложения на множители.

Метод введения новой переменной.

Метод замены уравнения уравнения f ( k ( x )) = f ( g ( x )) уравнением k ( x ) = g ( x )

Частный случай метода замены переменных (однородные уравнения)

Самостоятельная работа с использованием полученных знаний

Учитель предлагает учащимся вернуться в свои первоначальные группы.

Группы обмениваются карточками по кругу.

Задание каждому участнику группы: определить какое из предложенных уравнений решается методом, который он описывал на первом этапе урока.

Участники в группе по очереди называют номер своего уравнения, описывают соответствующий метод, ход решения.

Взаимооценка: учащиеся в группе оценивают выступление каждого участника (баллы от 1 до 3)

Систематизация знаний, проверка практических умений

Задание: проговорить друг другу методы решения предложенных 5 уравнений, записать решения в свою тетрадь.

Максимальное количество баллов за задание

1 Метод замены переменных

2.Метод разложения на множители

3. Однородные уравнения

4. Равносильные преобразования

Максимальное количество баллов – 6

Выполняют работу в рабочей тетради, выполняют взаимопроверку, проверяют по готовому слайду ответы, оценивают работу напарника. (баллы от 1 до 6)

Учащиеся выполняют работу, сверяют решения со слайдом. (за каждое верно выполненное 1 балл)

Оценивание, объяснение домашнего задания

Подсчитайте количество набранных вами баллов и переведите их в отметку.

Домашнее задание: 832(2) – замена равносильной системой,

838(5) – разложение на множители,

844(2) –замена переменных, 867(2), 853(1) – однородные,

№ 843 – задание повышенной сложности, необязательное задание.

Считают баллы, переводят в отметку.

Учащиеся записывают в дневник

Рефлексия учебной деятельности

Учитель предлагает учащимся заполнить анкету

На уроке я работал

Своей работой на уроке я

Урок для меня показался

Материал урока мне был

Домашнее задание мне кажется

Краткое описание документа:

Урок по математике разработан в соответствии с требованиями ФГОС ООО.

На уроке применяются современные образовательные технологии: технология развития критического мышления, технология проблемного обучения.

Содержание урока позволяет организовать активное усвоение учениками учебного материала, способствует максимальному использованию самостоятельности школьника в работе с информацией, формирует навыки не только индивидуальной работы, но и работы в коллективе, группе.

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 693 человека из 75 регионов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 864 человека из 78 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

• Сейчас обучается 48 человек из 23 регионов

«Профессиональный имидж педагога: стереотипы и методы их преодоления»

Свидетельство и скидка на обучение каждому участнику

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

Видео:Алгебра 7 класс (Урок№43 - Решение линейных уравнений с одним неизвестным.)Скачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 838 909 материалов в базе

Материал подходит для УМК

«Алгебра и начала математического анализа», Колягин Ю.М., Ткачёва М.В. и др.

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 25.12.2018
• 2096
• 61

• 23.12.2018
• 1058
• 31

• 18.12.2018
• 1893
• 32

• 17.12.2018
• 29133
• 362

• 16.12.2018
• 1821
• 10

• 16.12.2018
• 2078
• 21

• 16.12.2018
• 289
• 0

• 11.12.2018
• 273
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 08.01.2019 987
• DOCX 22.6 кбайт
• 16 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Ли Галина Валентиновна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 4 года и 8 месяцев
• Подписчики: 1
• Всего просмотров: 4409
• Всего материалов: 3

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Решение уравнений с одним неизвестным, сводящихся к линейным. Алгебра. 7 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

Российские школьники начнут изучать историю с первого класса

Время чтения: 1 минута

С 1 сентября в российских школах будут исполнять гимн России

Время чтения: 1 минута

Минпросвещения проведет Всероссийский конкурс для органов опеки и попечительства

Время чтения: 1 минута

«Единая Россия» внесла в Госдуму проект о снятии излишней нагрузки с учителей

Время чтения: 2 минуты

Опубликовано расписание ОГЭ 2022

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Методы решения уравнений — обзор

В этой статье дан краткий обзор всех основных методов решения уравнений. Здесь также приведены ссылки на материалы с подробной информацией по каждому методу. Это дает возможность познакомиться со всеми методами решения уравнений, а в случае необходимости — изучить методы решения уравнений углубленно.

Видео:Видеоурок. 7 класс. Решение линейных уравнений с одним неизвестнымСкачать

Метод введения новой переменной (замены переменной)

Метод введения новой переменной, он же метод замены переменной, позволяет решать уравнения f(g(x))=0 или f₁(g(x))=f₂(g(x)) , где f , f₁ и f₂ – некоторые функции, а x – неизвестная переменная, а также уравнения, которые могут быть приведены к указанному виду. Состоит метод во введении новой переменной t=g(x) . Введение переменной позволяет от исходного уравнения f(g(x))=0 или f₁(g(x))=f₂(g(x)) перейти к уравнению с новой переменной f(t)=0 или f₁(t)=f₂(t) соответственно. Дальше находятся корни полученного уравнения с новой переменной: t₁, t₂, …, t_n . После этого осуществляется возврат к старой переменной, для чего составляется совокупность уравнений g(x)=t₁, g(x)=t₂, …, g(x)=t_n . Решение этой совокупности дает интересующее нас решение исходного уравнения.

Например, метод введения новой переменной позволяет решить уравнение . Здесь стоит принять . Это позволяет перейти от исходного уравнения к квадратному уравнению t 2 −3·t+2=0 с новой переменной t , которое имеет два корня t₁=1 и t₂=2 . Обратная замена происходит путем составления совокупности двух уравнений и . Это рациональные уравнения. Решением первого является x=2 , а решением второго является x=1,5 . Так методом введения новой переменной получено решение исходного уравнения: 1,5 , 2 .

Подробное описание метода введения новой переменной, включающее обоснование метода, алгоритм решения уравнений этим методом и примеры решения характерных уравнений, дано в этой статье.

Видео:Математика 3 класс (Урок№3 - Решение уравнений с неизвестным уменьшаемым, с неизвестным вычитаемым.)Скачать

Метод разложения на множители

Метод разложения на множители предназначен для решения уравнений f₁(x)·f₂(x)·…·f_n(x)=0 , где f₁(x), f₂(x),…, f_n(x) – некоторые выражения, x – переменная. То есть, методом разложения на множители решаются уравнения, в левой части которых находится произведение нескольких выражений, а в правой – нуль. Суть метода состоит в замене решения уравнения f₁(x)·f₂(x)·…·f_n(x)=0 решением совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0 на области допустимых значений (ОДЗ) для исходного уравнения.

Приведем простой пример. Уравнение может быть решено методом разложения на множители. Переходим от исходного уравнения к совокупности двух уравнений и . Иррациональное уравнение имеет единственное решение x₁=1 . Логарифмическое уравнение тоже имеет единственное решение x₂=4 . Значит, совокупность уравнений имеет два решения x₁=1 , x₂=4 . Но области допустимых значений для исходного уравнения, которой является множество (3, +∞) , принадлежит лишь одно из решений x₁=1 , x₂=4 , а именно, x₂=4 . Оно и является единственным корнем уравнения .

Подробное описание этого метода и решения других характерных примеров смотрите в статье «метод разложения на множители».

Видео:Алгебра 7 Линейное уравнение с одной переменнойСкачать

Метод решения уравнений «дробь равна нулю»

Из названия понятно, что этот метод используется при решении уравнений f(x)/g(x)=0 . Например, он позволяет решить уравнение . Метод состоит в переходе от решения уравнения f(x)/g(x)=0 к решению уравнения f(x)=0 на ОДЗ для исходного уравнения. Следовательно, чтобы решить уравнение , надо решить уравнение (x−1)·(x 2 −4)=0 на ОДЗ для исходного уравнения.

Обоснование метода и примеры с решениями смотрите здесь.

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Метод решения уравнений через преобразования

Метод базируется на преобразовании уравнений с целью выстраивания последовательностей равносильных уравнений и уравнений-следствий со сравнительно простыми последними уравнениями, по решениям которых находятся решения исходных уравнений.

Например, для решения уравнения 3·x 4 −48=0 последовательно проводятся два преобразования: переносится слагаемое −48 из левой части уравнения в правую с противоположным знаком, после чего проводится деление обеих частей уравнения на число 3 . В результате получается равносильное уравнение x 4 =16 , причем очень простое в плане решения. Оно имеет два корня x₁=−2 и x₂=2 . Они и составляют решение исходного уравнения.

Вот другой пример. Замена выражения в левой части уравнения тождественно равным выражением (x−1)·(x+2) дает уравнение-следствие (x−1)·(x+2)=0 , имеющее два корня x₁=1 и x₂=−2 . Проверка показывает, что только первый корень является корнем исходного уравнения, а второй корень – посторонний.

Какие преобразования используются при решении уравнений? Когда нужно делать проверку для отсеивания посторонних корней, а когда такую проверку делать необязательно? Ответы на эти и многие другие вопросы по теме есть в этом материале.

Видео:Линейное уравнение с одним неизвестным.Скачать

Метод решения уравнений, сводящихся к числовым равенствам

Иногда в результате преобразования уравнений получаются числовые равенства. Например, уравнение сводится к верному числовому равенству 0=0 , а уравнение сводится к неверному числовому равенству 0=5 . Решением уравнений, сводящихся к верным числовым равенствам, является множество, совпадающее с ОДЗ для исходного уравнения. Так, решением уравнения является множество x≥0 . А уравнения, сводящиеся к неверным числовым равенствам, не имеют решений. То есть, уравнение не имеет решений.

Здесь есть один нюанс. Если среди преобразований, приводящих уравнение к верному числовому равенству, есть возведение обеих частей уравнения в одну и ту же четную степень, то нельзя утверждать, что решением уравнения является любое число из ОДЗ. Этот нюанс разобран в статье «решение уравнений, сводящихся к числовым равенствам».

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Функционально-графический метод

Обзор методов решения уравнений продолжаем функционально-графическии методом. Этот метод предполагает использование функций, отвечающих частям решаемого уравнения, а точнее, их графиков и свойств. Можно выделить три основных направления функционально-графического метода:

• Графический метод
• Метод, базирующийся на возрастании-убывании функций
• Метод оценки

Давайте рассмотрим их.

Графический метод

Первое направление базируется на использовании графиков функций. Это так называемый графический метод решения уравнений. По этому методу, во-первых, выполняется построение в одной прямоугольной системе координат графиков функций, отвечающих частям уравнения. Во-вторых, по чертежу определяется количество точек пересечения графиков, сколько точек пересечения – столько и корней у решаемого уравнения. В-третьих, определяются абсциссы точек пересечения – это значения корней.

Например, графически можно решить уравнение . Из чертежа, приведенного ниже, видно, что графики имеют единственную точку пересечения с абсциссой 2 . Это единственный корень уравнения.

Метод, базирующийся на возрастании-убывании функций

Второе направление в своей основе имеет использование свойств возрастающих и убывающих функций. Соответствующий метод используется тогда, когда есть возможность подобрать корень уравнения и доказать возрастание функции, отвечающей одной из частей уравнения, и убывание функции, отвечающей другой части уравнения. В этом случае подобранный корень является единственным.
Приведем пример. Для уравнения 3 (1−x) 3 +1=2 x несложно подобрать корень, им является число 1 . Также несложно обосновать убывание функции, соответствующей левой части уравнения, и возрастание функции, отвечающей правой части уравнения. Это доказывает единственность подобранного корня.

За более полной информацией следуйте сюда

Метод оценки

Третье направление основано на использовании свойств ограниченности функций. Это так называемый метод оценки. Согласно этому методу, в первую очередь нужно оценить значения выражений, находящихся в левой и правой части уравнения. Если множества, соответствующие полученным оценкам, не пересекаются, то уравнение не имеет корней. Если множества имеют конечное число общих элементов t₁ , t₂ , …, t_n , то решение уравнения f(x)=g(x) заменяется решением совокупности систем , , …, . Если же множества, соответствующие оценкам имеют бесконечно много общих элементов, то надо либо уточнять оценки, либо искать другой метод решения.

Например, методом оценки можно решить уравнение . Значения левой части этого уравнения не превосходят нуля, а значения правой части не меньше нуля. Это позволяет перейти к системе , решение которой дает искомое решение уравнения.

Видео:РЕШЕНИЕ УРАВНЕНИЙ |ПОДРОБНОЕ ОБЪЯСНЕНИЕ КАК РЕШИТЬ УРАВНЕНИЯ / ПРОСТЫЕ УРАВНЕНИЯ 2 КЛАСС МАТЕМАТИКАСкачать

Метод освобождения от внешней функции

Метод освобождения от внешней функции используется для решения уравнений h(f(x))=h(g(x)) , где f , g и h – функции, причем функция y=h(t) принимает каждое свое значение по одному разу, в частности, строго возрастает или строго убывает, а x – независимая переменная. Этот метод состоит в переходе от уравнения h(f(x))=h(g(x)) к уравнению f(x)=g(x) на ОДЗ для исходного уравнения.

Например, методом освобождения от внешней функции можно решить уравнение . Здесь в качестве внешней функции выступает y=h(t) , где . Эта функция возрастающая как сумма двух возрастающих функций и , значит, каждое свое значение она принимает по одному разу. Это позволяет перейти от исходного уравнения к уравнению . Равносильные преобразования позволяют привести последнее уравнение к квадратному уравнению x 2 +x−2=0 , которое имеет два корня x₁=−2 и x₂=1 . Из этих корней только x₁=−2 принадлежит ОДЗ для исходного уравнения. Следовательно, x₁=−2 – единственный корень исходного уравнения.

Рекомендуем детально разобраться с этим методом решения уравнений, обратившись к материалу статьи «метод освобождения от внешней функции».

Видео:Алгебра.7 класс (Урок№42 - Уравнения первой степени с одним неизвестным.)Скачать

Метод решения уравнений через ОДЗ

Через ОДЗ решаются уравнения, области допустимых значений которых являются либо пустыми множествами, либо состоят из конечного количества чисел. Когда ОДЗ есть пустое множество, уравнение не имеет решений. Когда ОДЗ состоит из конечного количества чисел, то следует по очереди проверить эти числа через подстановку. Те из них, которые удовлетворяют решаемому уравнению являются его корнями, остальные – не являются.

Например, уравнение не имеет решений, так как ОДЗ для него есть пустое множество. А для уравнения ОДЗ состоит из двух чисел −1 и 7 . Проверка подстановкой показывает, что −1 является корнем уравнения, а 7 – не является.

Более полная информация по этому методу решения уравнений содержится в этой статье.

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Метод возведения обеих частей уравнения в одну и ту же степень

Этот метод, в основном, используется для решения иррациональных уравнений. Он заключается в возведении обеих частей уравнения в одну и ту же степень с целью избавления от корней. Например, возведение обеих частей уравнения в квадрат дает уравнение без корня 1−5·x=(x−3) 2 . Возведение в нечетную степень дает равносильное уравнение. Возведение в четную степень в общем случае дает уравнение-следствие, поэтому, при этом необходимо позаботиться об отсеивании посторонних корней. Причем отсеивание следует проводить способом, не связанным с ОДЗ, обычно, через проверку подстановкой, так как возведение частей уравнения в четную степень может приводить к появлению посторонних корней в рамках ОДЗ.

Аналогично разбираемый метод может использоваться и для решения уравнений, в которых фигурируют степени с рациональными и иррациональными показателями. Решения соответствующих примеров смотрите здесь.

Видео:Решение систем уравнений методом подстановкиСкачать

Метод решения уравнений по определению логарифма

По определению логарифма, как правило, решают уравнения следующего вида log_h(x)f(x)=g(x) , например, log₂(x 2 +4·x+3)=3 , log₂(9−2 x )=3−x , log_x(3·x lgx +4)=2·lgx и т.п.

Согласно методу решения уравнений по определению логарифма, решение уравнения log_h(x)f(x)=g(x) заменяется решением уравнения f(x)=(h(x)) g(x) на ОДЗ переменной x для исходного уравнения. Например, от уравнения log_x(3·x lgx +4)=2·lgx можно перейти к уравнению 3·x lgx +4=x 2·lgx на ОДЗ для исходного уравнения.

Более полная информация содержится в основной статье.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Метод потенцирования

Методом потенцирования решаются логарифмические уравнения, обе части которых являются логарифмами по одному и тому же основанию, например, lgx=lg(3·x+5) , и т.п. Метод заключается в замене решения уравнения log_h(x)f(x)=log_h(x)g(x) решением уравнения f(x)=g(x) на ОДЗ для исходного уравнения. По этому методу от уравнения lgx=lg(3·x+5) следует перейти к уравнению x=3·x+5 на ОДЗ для исходного уравнения, которая определяется двумя условиями: x>0 , 3·x+5>0 .

Обоснование метода и примеры с подробными решениями смотрите в этой статье.

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Метод логарифмирования

Метод подразумевает логарифмирование обеих частей уравнения по одному и тому же основанию. К нему следует прибегать тогда, когда логарифмирование позволяет избавиться от степеней с переменной в показателях. В частности, его можно использовать для решения показательных уравнений, обе части которых являются степенями с одинаковыми основаниями, например, 5 1−x =5 2·x+1 . Почленное логарифмирование этого уравнения дает очень простое уравнение 1−x=2·x+1 , решение которого дает решение исходного уравнения.

Также метод подходит для решения показательных уравнений, степени в которых имеют разные основания и отличающиеся показатели, например, . Более того, метод логарифмирования является чуть ли не основным методом решения показательно-степенных уравнений, вроде таких x lgx−1 =100 , .

Более детальная информация и примеры с решениями есть в этом материале.

💡 Видео

Простые уравнения. Как решать простые уравнения?Скачать

Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Как решать уравнения с дробью? #shortsСкачать

УРАВНЕНИЕ 4 КЛАСС МАТЕМАТИКА УЧИМСЯ РЕШАТЬ УРАВНЕНИЯ МЕТОДИКА ОБУЧЕНИЯ РЕШАЕМ УРАВНЕНИЯ #уравнениеСкачать