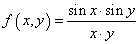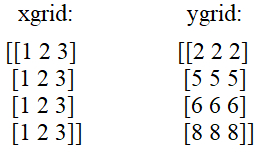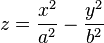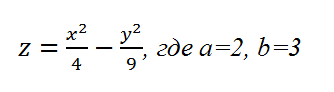Как строить трехмерные графики по уравнению

Следующим шагом мы с вами рассмотрим возможности построения трехмерных графиков в пакете matplotlib. Такая возможность появилась, начиная с версии 0.99, поэтому убедитесь, что ваш пакет поддерживает трехмерные графики.

Все дополнительные классы для работы в 3D находятся в модуле:

и вначале мы его импортируем в нашу программу наряду с самим пакетом matplotlib и numpy:

А, затем, создадим трехмерную систему координат:

При выполнении этой простой программы, мы в окне увидим три пространственные оси, которые можно вращать с помощью курсора мышки:

Того же самого результат можно добиться, используя параметр projection при создании системы координат:

Как именно создавать трехмерные оси, зависит от вашего выбора и удобства при написании конкретных программ. Я остановлюсь на втором способе.

После создания координатных осей мы можем в них строить двумерные и трехмерные графики с помощью того же самого набора функций:

• plot() – линейный 2D график в трех измерениях;
• step() – ступенчатый 2D график в трех измерениях;
• scatter() – точеный график 3D график.

Также нам становятся доступными следующие дополнительные функции:

• plot_wireframe() – построение каркасной поверхности в 3D;
• plot_surface() – построение непрерывной 3D поверхности.

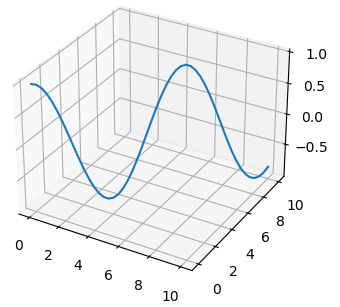
Начнем с самого простого варианта – функции plot() для рисования косинусоиды в трех измерениях:

То есть, мы здесь по координатам x, y выбираем одни и те же значения, а координата z (вертикаль) – это значение функции. Давайте подпишем оси, чтобы видеть, где какая расположена на этом графике:

Но то, что мы получили, это не совсем трехмерный график. Скорее, это двумерная косинусоида в трех измерениях. Давайте построим настоящее трехмерное изображение, например, вот такой функции:

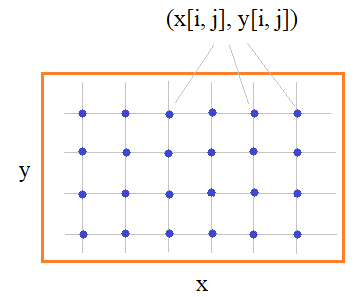
Первое, что нам здесь нужно сделать – это сформировать двумерную сетку координат по осям x и y:

То есть, должны быть сформированы двумерные массивы x, y, которые для текущей точки с индексами (i, j) возвращают ее координаты в плоскости xy.

Для регулярных сеток эти массивы можно сформировать следующим образом. Определим множество координат x (для столбцов) и y (для строк), например, так:

А, затем, используя функцию meshgrid() сформируем регулярную сетку на основе этих данных:

На выходе получим двумерные массивы со значениями:

То есть, смотрите, теперь для любой пары индексов (i, j) мы легко сможем получить координаты точки в плоскости xy:

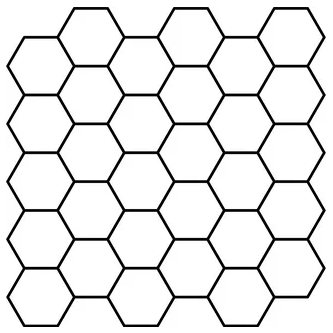
Но зачем было так все усложнять? Почему бы не использовать одномерные массивы x, y вместо двумерных xgrid, ygrid? Дело в том, что одномерные массивы, которые описывают расположение строк и столбов, могут формировать только регулярные сетки, то есть, прямоугольные. А что, если нужно сформировать гексагональную сетку, которая выглядит, следующим образом:

Здесь уже не получится обойтись указанными одномерными массивами, а нужно прописывать узлы двумерными массивами. Именно поэтому, в общем случае, и реализовано отображение через двумерные массивы трехмерных графиков.

Итак, давайте теперь построим полноценный трехмерный график синусоиды на регулярной сетке. Для этого мы сначала сформируем координаты узлов в плоскости xy:

А, затем, вычислим значения синусоиды в этих узлах:

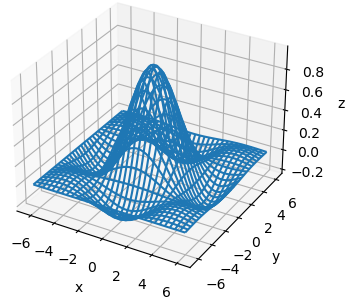
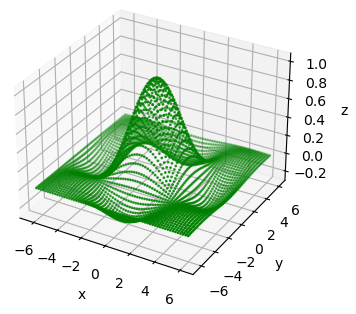
Если для вывода такого графика воспользоваться функцией plot_wireframe():

то результат будет следующий:

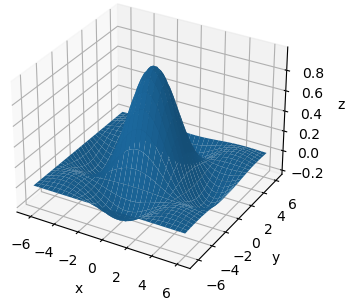
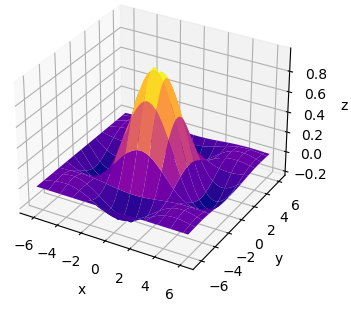
Как видите, мы получили полноценный каркасный трехмерный график синусоиды. Или же можно построить полноценную поверхность в виде синусоиды, используя функцию plot_surface():

Фактически, только этим две эти функции и отличаются друг от друга: первая строит 3D-каркас, а вторая 3D-поверхность.

У этих функций есть следующие параметры для настройки внешнего вида графика:

Параметр

Описание

x, y, z

2D массивы для построения трехмерных графиков.

rcount, ccount

Максимальное число элементов каркаса по координатам x и y (по умолчанию 50).

rstride, cstride

Величина шага, с которым будут выбираться элементы из массивов x, y (параметры rstride, cstride и rcount, ccount – взаимоисключающие).

color

Цвет графика

Цветовая карта графика

Например, если установить параметры:

то получим следующий вид нашей синусоиды:

В заключение этого занятия приведу пример построения этого же графика набором точек, используя функцию scatter():

Увидим следующий результат:

Вот так в базовом варианте можно выполнять построения трехмерных графиков в пакете matplotlib. Этой информации достаточно для большинства прикладных задач. Ну а если потребуется реализовать что-то особенное, тогда прямой путь к документации:

Видео по теме

#1. Установка пакета и основные возможности

#2. Функция plot для построения и оформления двумерных графиков

#3. Отображение нескольких координатных осей в одном окне

#4. Граничные значения осей и локаторы для расположения меток на них

#5. Настраиваем формат отображения меток у координатных осей

#6. Делаем логарифмический масштаб у координатных осей

#7. Размещаем стандартные текстовые элементы на графике

#8. Добавляем легенду и рисуем геометрические фигуры на графиках

#9. Рисуем ступенчатые, стековые, stem и точечные графики

#10. Рисуем гистограммы, столбчатые и круговые диаграммы

#11. Показ изображений и цветовых сеток

#12. Как строить трехмерные графики

#13. Рисуем линии уровня функциями contour, contourf и tricontour, tricontourf

#14. Создаем анимацию графиков Классы FuncAnimation и ArtistAnimation

© 2022 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта

Видео:Урок 3. 3D-поверхности в excel.Скачать

Как строить трехмерные графики по уравнению

График поверхности, заданной явной функцией.

График функции можно нарисовать, используя команду plot3d(f(x,y), x=x1…x2, y=y1…y2, options) . Параметры этой команды частично совпадают с параметрами команды plot. К часто используемым параметрам команды plot3d относится light=[angl1, angl2, c1, c2, c3] – задание подсветки поверхности, создаваемой источником света из точки со сферическими координатами ( angl1 , angl2 ). Цвет определяется долями красного ( c1 ), зеленого ( c2 ) и синего ( c3 ) цветов, которые находятся в интервале [0,1]. Параметр style=opt задает стиль рисунка: POINT –точки, LINE – линии, HIDDEN – сетка с удалением невидимых линий, PATCH – заполнитель (установлен по умолчанию), WIREFRAME – сетка с выводом невидимых линий, CONTOUR – линии уровня, PATCHCONTOUR – заполнитель и линии уровня. Параметр shading=opt задает функцию интенсивности заполнителя, его значение равно xyz – по умолчанию, NONE – без раскраски.

График поверхности, заданной параметрически.

Если требуется построить поверхность, заданную параметрически: x = x ( u , v ), y = y ( u , v ), z = z ( u , v ), то эти функции перечисляются в квадратных скобках в команде: plot3d([x(u,v), y(u,v), z(u,v)], u=u1..u2, v=v1..v2) .

График поверхности, заданной неявно.

Трехмерный график поверхности, заданной неявно уравнением , строится с помощью команды пакета plot: implicitplot3d(F(x,y,z)=c, x=x1..x2, y=y1..y2, z=z1..z2), где указывается уравнение поверхности и размеры рисунка по координатным осям.

График пространственных кривых.

В пакете plot имеется команда spacecurve для построения пространственной кривой, заданной параметрически: . Параметры команды :

где переменная t изменяется от t1 до t2 .

Maple позволяет выводить на экран движущиеся изображения с помощью команд animate (двумерные) и animate3d (трехмерные) из пакета plot . Среди параметров команды animate3d есть frames – число кадров анимации (по умолчанию frames=8 ).

Трехмерные изображения удобнее настраивать не при помощи опций команды plot3d , а используя контекстное меню программы. Для этого следует щелкнуть правой кнопкой мыши по изображению. Тогда появится контекстное меню настройки изображения. Команды этого меню позволяют изменять цвет изображения, режимы подсветки, устанавливать нужный тип осей, тип линий и управлять движущимся изображением.

Контекстное меню настройки изображения:

Видео:#12. Как строить трехмерные графики | Matplotlib урокиСкачать

Задание 2.

Выполнить построение двух поверхностей и в пределах . Установите переменный цвет поверхностей как функцию .

Построить поверхность вместе с линиями уровня:

> plot3d(1/(x^2+y^2)+0.2/((x+1.2)^2+(y-1.5)^2)+ 0.3/((x-0.9)^2+(y+1.1)^2), x=-2..2, y=-2..2.5, view=[-2..2, -2..2.5, 0..6], grid=[60,60], shading=NONE, light=[100,30,1,1,1], axes=NONE, orientation=[65,20], style=PATCHCONTOUR);

Построить примерную форму электронного облака атома. Форма электронного облака определяется двумя квантовыми числами: число l – определяет тип орбитали, число m – определяет магнитный момент электрона. При m =0 форма электронного облака задается полиномами Лежандра первого рода: . Следует построить параметрически заданную поверхность: , , , где . Вначале положите l =3. Наберите команды:

Видео:Поверхности в Excel (Surface in Excel)Скачать

Построить трехмерный график по точкам

Для задания области (например, 1≤x≤7 ) используйте пределы или >= .

Видео:Как построить график функции без таблицыСкачать

Трехмерные графики функции

Чтобы создать трехмерный график достаточно, чтобы в выражении была переменная y (например, y^2-x/3 ).

• График функции онлайн
• График по точкам
• Построение графика в Excel

Чтобы создать трехмерный график достаточно, чтобы в выражении была переменная y (например, y^2-x/3 ).

Чтобы построить трехмерный график в Excel , необходимо указать функцию f(x,y) , пределы по x и y и шаг сетки h .

Видео:Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать

Принципы и способы построения графика функции

Видео:Самые ЗАДИЗЛАЙКАННЫЕ уровни КАЖДОЙ сложностиСкачать

Прикладное применение графика функции

Построить пирамиду ABCD по координатам можно здесь.

Видео:Построение трехмерного графика в MathCAD 14 (14/34)Скачать

Введение

Визуализация — важная часть анализа данных, а способность посмотреть на несколько измерений одновременно эту задачу облегчает. В туториале мы будем рисовать графики вплоть до 6 измерений.

Plotly — это питоновская библиотека с открытым исходным кодом для разнообразной визуализации, которая предлагает гораздо больше настроек, чем известные matplotlib и seaborn. Модуль устанавливается как обычно — pip install plotly. Его мы и будем использовать для рисования графиков.

Видео:Основы работы в Mathcad ГрафикиСкачать

Давайте подготовим данные

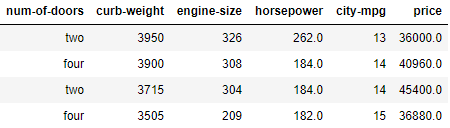
Для визуализации мы используем простые данные об автомобилях от UCI (Калифорнийский университет в Ирвине — прим. перев.), которые представляют собой 26 характеристик для 205 машин (26 столбцов на 205 строк). Для визуализации шести измерений мы возьмём такие шесть параметров.

Загрузим данные из CSV с помощью pandas.

Теперь, подготовившись, начнем с двух измерений.

Видео:Построение графиковСкачать

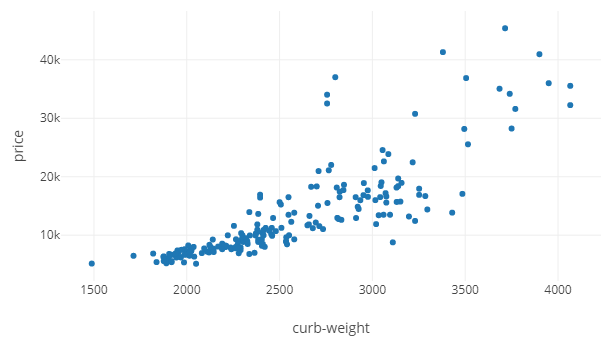
Двухмерная диаграмма рассеяния

Диаграмма рассеяния — весьма простой и распространенный график. Из 6 параметров, price и curb-weight используются ниже как Y и X соответственно.

В plotly процесс немного отличен от аналогичного в Matplotlib. Мы должны создать layout и figure, передав их в функцию offline.plot, после чего результат будет сохранён в HTML файл в текущей рабочей директории. Вот скриншот того, что получится. В конце статьи будет ссылка на GitHub репозиторий с готовыми интерактивными HTML-графиками.

Видео:Математика это не ИсламСкачать

Диаграмма рассеяния в 3D

Мы можем добавить третий параметр horsepower (количество лошадиных сил) на ось Z. Plotly предоставляет функцию Scatter3D для построения интерактивных трёхмерных графиков.

Вместо того чтобы вставлять код сюда каждый раз, я добавлял его в репозиторий.

(Удобнее всего смотреть релевантный код в соседней вкладке параллельно со чтением — прим. перев.)

Видео:Олегу Тинькову запрещён вход на Мехмат МГУСкачать

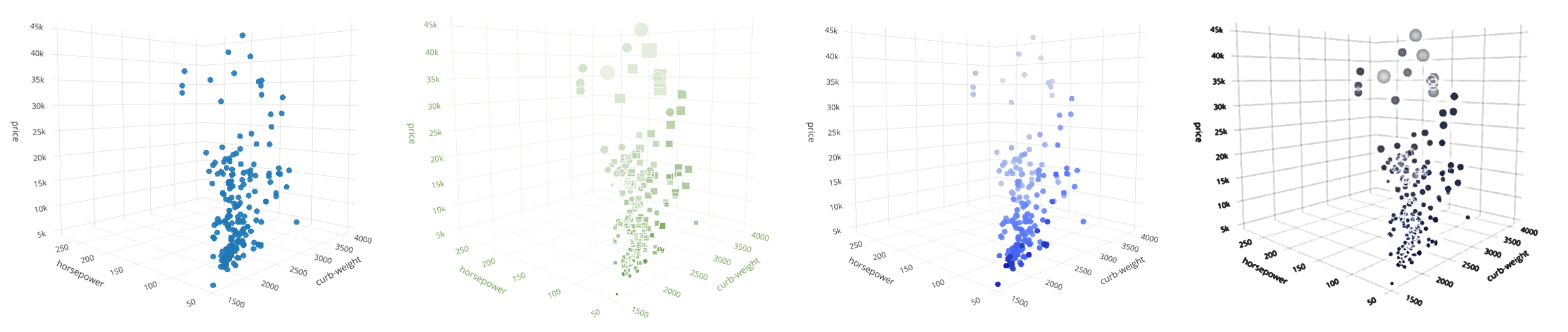
Добавление четвёртого измерения

Мы знаем, что использовать больше трёх измерений напрямую нельзя, но есть обходной путь: мы можем эмулировать глубину для визуализации более высоких измерений с помощью цвета, размера или формы.

Здесь, наряду с тремя предыдущими характеристиками, мы будем использовать пробег в городских условиях — city-mpg как четвертое измерение, за которое будет отвечать параметр markercolor функции Scatter3D. Более светлый оттенок маркера будет означать меньший пробег.

Сразу же бросается в глаза, что чем выше цена, количество лошадей и масса, тем меньше будет пробег.

Видео:Алгебра 9 класс. Графический способ задания функцииСкачать

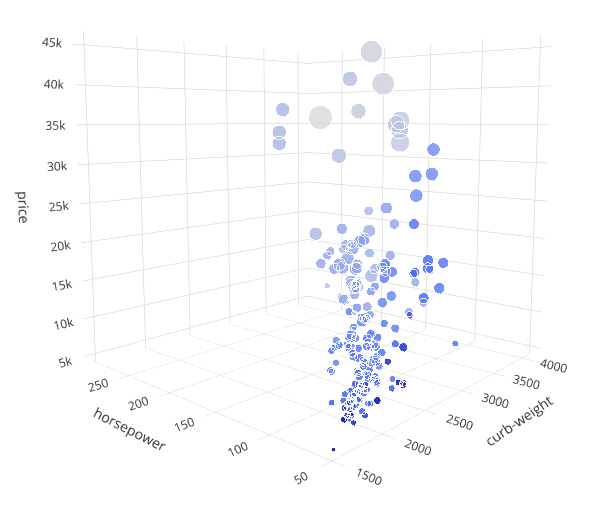
Добавление пятого измерения

Размер маркера можно использовать для визуализации 5-го измерения. Мы используем характеристику engine-size (размер двигателя) для параметра markersize функции Scatter3D.

Наблюдения: размер двигателя связан с некоторыми из предыдущих параметров. Чем выше цена, тем больше двигатель. Ра́вно как и: ниже пробег — больше двигатель.

Видео:Вопрос-ответ с астрономом Владимиром Сурдиным – Самые популярные вопросыСкачать

Добавление шестого измерения

Форма маркера отлично подходит для визуализации категорий. Plotly даёт на выбор 10 различных фигур для 3D графика (звёздочка, круг, квадрат и т.д.). Таким образом, в качестве формы можно показать до 10 различных значений.

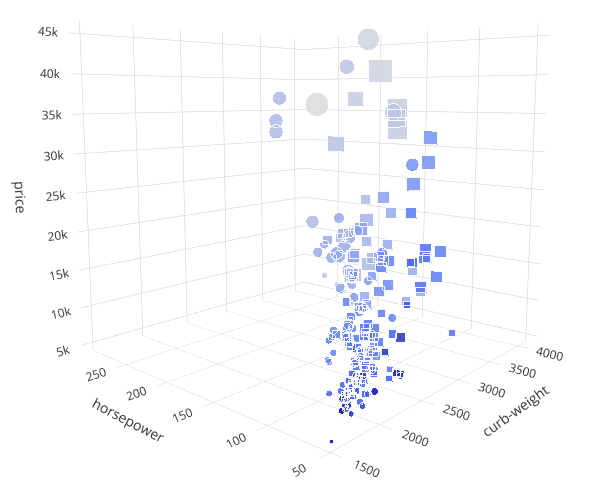
У нас есть характеристика num-of-doors, которая содержит целые числа — количество дверей (2 или 4). Преобразуем эти значения в фигуры: квадрат для 4 дверей, круг для 2 дверей. Используется параметр markersymbol функции Scatter3D.

Наблюдения: такое чувство, что у всех самых дешёвых машин по 4 двери (круги). Продолжая изучать график, можно будет сделать больше предположений и выводов.

6D график с формой маркера в качестве шестого измерения (количество дверей)

Видео:MatLab. Создание 3D графиков. Практика 4Скачать

Можем ли мы добавить больше измерений?

Конечно можем! У маркеров есть больше свойств, таких как непрозрачность и градиенты, которые можно задействовать. Но чем больше измерений мы добавляем, тем труднее удержать их все в голове.

Видео:Исследование функции. Построение графика. Высшая математикаСкачать

Исходный код

Код на Python и интерактивные графики для всех фигур доступны на GitHub здесь.

В продолжении темы о графиках функций в Excel расскажу о построении трехмерных графиков.

Трехмерный график функции — это график в трех измерениях. Соответственно каждая точка графика будет иметь три координаты (x, y. z).

Построим график функции, называемый гиперболический параболоид, в Excel.

Уравнение гиперболического параболоида (общий вид):

где x, y, z — переменные; a, b — константы.

Рассмотрим конкретный случай:

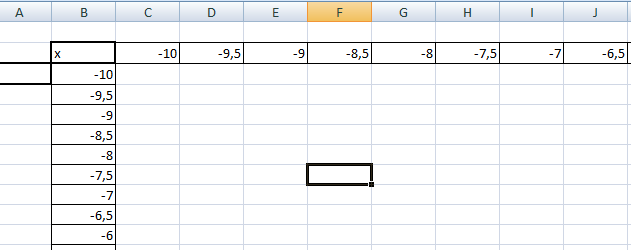
Как и для построения графика функции на плоскости нам потребуется таблица, на основании которой график и будет построен.

по горизонтали — значения х, по вертикали — значения у.

Значения z вычисляются по формуле (см. выше). Запишем формулу для вычисления z, где x=10, y = 10, a=2, b=3.

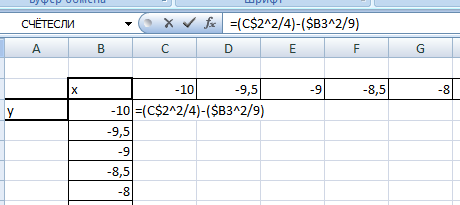
Для того, чтобы эта формула правильно копировалась с помощью маркера автозаполнения необходимо верно поставить знаки $ в формулу.

=(C$2^2/4)-($B3^2/9) , для ячейки со значением x фиксируем номер строки, для ячейки со значением y фиксируем букву столбца.

Используя маркер автозаполнения, копируем формулу для всех значений x и y.

Получим таблицу, в которой каждой паре (x, y) соответствует координата z.

Выделяем диапазон ячеек со значениями z, выбираем ВСТАВКА — ДРУГИЕ ДИАГРАММЫ — ПОВЕРХНОСТЬ

🎬 Видео

Построение графика поверхностиСкачать

Математический анализ, 16 урок, Исследование функции и построение графикаСкачать

Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Как строить графики без таблицСкачать

Как в excel построить графикСкачать