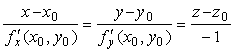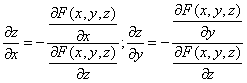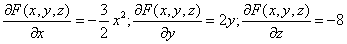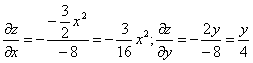Как составить уравнение касательной параллельной плоскости (5 видео)

Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M₀(x₀,y₀,z₀) имеет вид:

Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M₀(0;1).
Решение. Запишем уравнения касательной в общем виде: z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 0 , y₀ = 1 , тогда z₀ = 5
Найдем частные производные функции z = x^3+5*y :
f’_x(x,y) = (x 3 +5•y)’_x = 3•x 2
f’_x(x,y) = (x 3 +5•y)’_y = 5
В точке М₀(0,1) значения частных производных:
f’_x(0;1) = 0
f’_y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 5 = 0(x — 0) + 5(y — 1) или -5•y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M₀(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М₀(1,0,1) значения частных производных:
f’_x(1;0;1) = -3 /₁₆
f’_y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 1 = -3 /₁₆(x — 1) + 0(y — 0) или 3 /₁₆•x+z- 19 /₁₆ = 0

Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀ = –1, y₀ = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
f_x’(x, y) = (y/x + xy – 5x 3 )’_x = – y/x 2 + y – 15x 2 ;
f_y’ (x, y) = (y/x + xy – 5x 3 )’_y = 1/x + x.
Точка М₀(x₀, y₀, z₀) принадлежит поверхности σ, поэтому можно вычислить z₀, подставив заданные x₀ = –1 и y₀ = 2 в уравнение поверхности:

Пример №1 . Дана функция z=f(x,y) и две точки А(х₀, y₀) и В(х₁,y₁). Требуется: 1) вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение z₁ функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x₀,y₀,z₀).
Решение.
Запишем уравнения касательной в общем виде:
z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 1, y₀ = 2, тогда z₀ = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_x = 2•x+3•y 3
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_y = 9•x•y 2
В точке М₀(1,2) значения частных производных:
f’_x(1;2) = 26
f’_y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение

Содержание

Математический портал
Nav view search
Navigation
Search
Касательная плоскость и нормаль к явно заданной поверхности.
Касательная плоскость и нормаль к поверхности.
🔥 Видео

Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

Математический портал

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Nav view search

Search

Вы здесь:
Home
Математический анализ
Касательная плоскость и нормаль к явно заданной поверхности.

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Касательная плоскость и нормаль к явно заданной поверхности.

Касательной плоскостью к поверхности в ее точке $M_0$ (точка касания) называется плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку.

Нормалью к поверхности называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.

Если уравнение поверхности имеет вид $$F(x,y,z)=0,$$ то уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ есть $$F_x'(x_0, y_0, z_0)(x-x_0)+F_y'(x_0, y_0, z_0)(y-y_0)+F_z'(x_0, y_0, z_0)(z-z_0)=0.$$

В случае задания поверхности в явной форме $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$frac=frac=frac.$$

Примеры:

7.229. а) Найти уравнения касательной плоскости и нормали к поверхности $z=sin xcos y$ в точке $(pi/4, pi/4, pi/4).$

Решение.

Для поверхности $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$frac=frac=frac.$$

Находим частные производные:

$z’_x=(sin xcos y)’_x=cos xcos y;$

$z’_y=(sin xcos y)’_y=-sin xsin y;$

Таким образом, уравнение касательной плоскости: $$z-frac=frac(x-frac)-frac(y-frac)Rightarrow$$ $$fracx -fracy-z+frac=0.$$

7.232. Для поверхности $z=4x-xy+y^2$ найти уравнение касательной плоскости, параллельной плоскости $4x+y+2z+9=0.$

Решение.

Для поверхности $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0).$$

Находим частные производные:

Отсюда находим уравнение касательной плоскости: $$z-z_0=(4-y_0)(x-x_0)+(-x_0+2y_0)(y-y_0)Rightarrow$$ $$(4-y_0)(x-x_0)+(-x_0+2y_0)(y-y_0)-z+z_0=0.$$

Найдем точку поверхности $M(x_0, y_0, x_0)$ касательная плоскость к которой будет параллельна плоскости $4x+y+2z+9=0:$

Таким образом, уравнение касательной плоскости: $$z-11=(4-6)(x-frac)+(-frac+2cdot 6)(y-6)Rightarrow$$ $$z-11=-2(x-frac)-frac(y-6)Rightarrow 2x+fracy+z-11-25-3=0Rightarrow$$ $$Rightarrow4x+y+2z-78=0.$$

7.233. а) Найти уравнения касательной плоскости и нормали к поверхности $x(y+z)(xy-z)+8=0$ в точке $(2, 1, 3).$

Решение.

Для поверхности $$F(x,y,z)=0,$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ есть $$F_x'(x_0, y_0, z_0)(x-x_0)+F_y'(x_0, y_0, z_0)(y-y_0)+F_z'(x_0, y_0, z_0)(z-z_0)=0.$$

$F(x, y, z)=x(y+z)(xy-z)+8=x^2y^2-xyz+x^2yz-xz^2+8=0$

Находим частные производные:

Отсюда находим уравнение касательной плоскости: $$4(x-2)+14(y-1)-10(z-3)=0Rightarrow 4x+14y-10z+8.$$

Домашнее задание.

7.229. б) Найти уравнения касательной плоскости и нормали к поверхности $z=e^$ в точке $(1, pi/ 1/e).$

7.230. Найти расстояние от начала координат до касательной плоскости к поверхности $z=y tgfrac$ в точке $left(fracright).$

7.233. б) Найти уравнения касательной плоскости и нормали к поверхности $2^+2^=8$ в точке $(2, 2, 1).$

7.234. Для поверхности $x^2-z^2-2x+6y=4$ найти уравнение нормали, параллельной прямой $frac=frac=frac.$

Видео:Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.Скачать

Касательная плоскость и нормаль к поверхности.

Пусть поверхность задана в неявном виде: $F(x,y,z)=0$ и пусть точка $M_0(x_0,y_0,z_0)$ принадлежит данной поверхности. Тогда уравнение касательной плоскости к этой поверхности в точке $M_0$ таково:

Уравнение нормали имеет вид:

Если же уравнение поверхности задано в явном виде $z=f(x,y)$, то уравнение касательной плоскости имеет вид:

Уравнение нормали в случае явного задания поверхности таково:

Примечание (желательное для более полного понимания текста): показатьскрыть

Формулы (3) и (4) легко получить из формул (1) и (2). Если $z=f(x,y)$, то перенося $z$ в правую часть равенства получим: $f(x,y)-z=0$. Обозначая $F(x,y,z)=f(x,y)-z$, получим: $F_^=left(f(x,y)-zright)_^=f_^(x,y)-0=f_^(x,y)$. Аналогично и $F_^=left(f(x,y)-zright)_^=f_^(x,y)-0=f_^(x,y)$. Что же касается последней производной (т.е. производной по переменной $z$), то тут нужно учесть, что выражение $f(x,y)$ не содержит $z$, поэтому: $F_^=left(f(x,y)-zright)_^=0-1=-1$. Подставляя в формулы (1) и (2) вместо $F_^$, $F_^$, $F_^$ соответственно $f_^$, $f_^$ и $-1$ и получим формулы (3) и (4).

Найти уравнение касательной плоскости и нормали к поверхности $z=3x^2y^4-6xy^3+5x-4y+10$ в точке $M_0(-2;1;20)$.

Поверхность задана в явном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (3) и (4). Значения $x_0$, $y_0$, $z_0$ (координаты точки $M_0$) в нашем случае таковы: $x_0=-2$, $y_0=1$, $z_0=20$. Но перед тем, как переходить к решению, осуществим небольшую проверку. Убедимся, что точка $M_0$ действительно лежит на заданной поверхности. Эта проверка не является обязательной, но желательна, ибо ошибка в условиях подобных задач – дело вовсе не редкое. Подставим $x=x_0$, $y=y_0$ в уравнение нашей поверхности и убедимся, что $z_0$ действительно равно 20:

$$ z_0=3x_^y_^-6x_0y_^+5x_0-4y_0+10=3cdot (-2)^2cdot 1^4-6cdot (-2)cdot 1^3-4cdot 1+10=12+12-4=20. $$

Проверка пройдена, точка $M_0$ действительно лежит на заданной поверхности. Теперь найдём частные производные, т.е. $z_^$ и $z_^$:

Нас интересуют значения частных производных именно в точке $M_0$, посему подставим $x=x_0$, $y=y_0$ в выражения частных производных:

Подставляя $x_0=-2$, $y_0=1$, $z_0=20$, $z_^ left(x_0, y_0right)=-13$, $z_^ left(x_0, y_0right)=80$ в формулу (3) получим уравнение касательной плоскости:

Подставляя $x_0=-2$, $y_0=1$, $z_0=20$, $z_^ left(x_0, y_0right)=-13$, $z_^ left(x_0, y_0right)=80$ в формулу (4) получим уравнение нормали:

Ответ: Касательная плоскость: $-13x+80y-z-86=0$; нормаль: $frac=frac=frac$.

Найти уравнение касательной плоскости и нормали к поверхности $z=5sqrt-2xy-39$ в точке $M_0(3;-4;z_0)$.

Поверхность задана в явном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (3) и (4). Значения $x_0$ и $y_0$ (первая и вторая координаты точки $M_0$) заданы по условию: $x_0=3$, $y_0=-4$. Третью координату (т.е. $z_0$) нужно определить самостоятельно, подставив в заданное уравнение $x=x_0$ и $y=y_0$:

Теперь, как и в предыдущем примере, перейдём к нахождению частных производных $z_^$ и $z_^$. После того, как мы найдём эти производные в общем виде, укажем их значения при $x=x_0$ и $y=y_0$:

Подставляя $x_0=3$, $y_0=-4$, $z_0=10$, $z_^ left(x_0, y_0right)=11$, $z_^ left(x_0, y_0right)=-10$ в формулы (3) и (4) получим уравнения касательной плоскости и нормали:

Ответ: Касательная плоскость: $11x-10y-z-63=0$; нормаль: $frac=frac=frac$.

Найти уравнение касательной плоскости и нормали к поверхности $3xy^2z+5xy+z^2=10xz-2y+1$ в точке $M_0(1;-2;3)$.

Перенесём все слагаемые в левую часть равенства и обозначим полученное в левой части выражение как $F(x,y,z)$:

Используем формулы (1) и (2). Значения $x_0$, $y_0$ и $z_0$ как и ранее обозначают координаты точки $M_0$, т.е. $x_0=1$, $y_0=-2$, $z_0=3$.

Проверим, действительно ли точка $M_0$ лежит на данной поверхности. Для этого подставим $x=x_0$, $y=y_0$ и $z=z_0$ в выражение $3xy^2z+5xy+z^2-10xz+2y-1$ и выясним, равен ли нулю полученный результат:

Итак, точка $M_0$ действительно лежит на данной поверхности. Естественно, что данная проверка не является обязательной, но она крайне желательна. Перейдём к дальнейшему решению. Нам нужно найти $F_^$, $F_^$ и $F_^$:

Нас интересуют значения частных производных именно в точке $M_0$, посему подставим $x=x_0$, $y=y_0$ и $z=z_0$ в выражения частных производных:

Подставляя $x_0=1$, $y_0=-2$, $z_0=3$, $F_^ left(M_0right)=-4$, $F_^ left(M_0right)=-29$ и $F_^ left(M_0right)=8$ в формулы (1) и (2) получим уравнения касательной плоскости и нормали:

Ответ: Касательная плоскость: $-4x-29y+8z-78=0$; нормаль: $frac=frac=frac$.

Найти уравнение касательной плоскости и нормали к поверхности $z^3+4xyz=-3x^2+5y+7$ в точке $M_0(0;-3;z_0)$.

Поверхность задана в неявном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (1) и (2). Значения $x_0$ и $y_0$ (первая и вторая координаты точки $M_0$) заданы по условию: $x_0=0$, $y_0=-3$. Третью координату (т.е. $z_0$) нужно определить самостоятельно, подставив в заданное уравнение $x=x_0$ и $y=y_0$:

Перенесём все слагаемые в левую часть равенства:

Обозначим $F(x,y,z)=z^3+4xyz+3x^2-5y-7$ и применим формулы (1) и (2). Найдём частные производные первого порядка $F_^$, $F_^$ и $F_^$. После того, как мы найдём эти производные в общем виде, укажем их значения в точке $M_0$:

Подставляя $x_0=0$, $y_0=-3$, $z_0=-2$, $F_^ left(M_0right)=-24$, $F_^ left(M_0right)=-5$ и $F_^ left(M_0right)=12$ в формулы (1) и (2) получим уравнения касательной плоскости и нормали:

Ответ: Касательная плоскость: $-24x-5y+12z+9=0$; нормаль: $frac=frac=frac$.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).