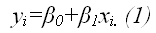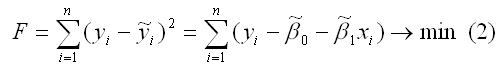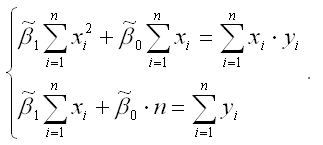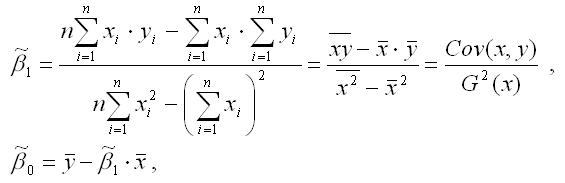Как составить нормальную систему уравнений

Видео:Решение систем уравнений методом подстановкиСкачать

Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессии

Предположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида:

В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

Метод наименьших квадратов позволяет получить такие оценки параметров β₀и β₁, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) y˜ минимальна:

В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β₀ и β₁, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):

.

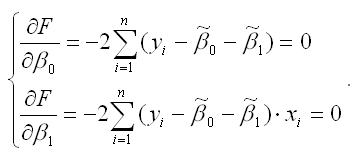
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=β₀+β₁xi:

Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β₀ и β₁:

y – среднее значение зависимой переменной;

x – среднее значение независимой переменной;

xy – среднее арифметическое значение произведения зависимой и независимой переменных;

G 2 (x) – дисперсия независимой переменной;

Gcov (x, y) – ковариация между зависимой и независимой переменными.

Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом:

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

23. Нормальные системы линейных однородных дифференциальных

Уравнений с постоянными коэффициентами.

При рассмотрении систем дифференциальных уравнений ограничимся случаем системы трех уравнений (n = 3). Все нижесказанное справедливо для систем произвольного порядка.

Определение. Нормальная система дифференциальных уравнений c постоянными коэффициентами называется Линейной однородной, если ее можно записать в виде:

(2)

Решения системы (2) обладают следующими свойствами:

Решения системы ищутся в виде:

Подставляя эти значения в систему (2) и перенеся все члены в одну сторону и сократив на Ekx, получаем:

Для того, чтобы полученная система имела ненулевое решение необходимо и достаточно, чтобы определитель системы был равен нулю, т. е.:

В результате вычисления определителя получаем уравнение третьей степени относительно K. Это уравнение называется Характеристическим уравнением И имеет три корня K1, K2, K3. Каждому из этих корней соответствует ненулевое решение системы (2):

Линейная комбинация этих решений с произвольными коэффициентами будет решением системы (2):

Пример. Найти общее решение системы уравнений:

Составим характеристическое уравнение:

Решим систему уравнений:

Для K1:

Полагая (принимается любое значение), получаем:

Для K2:

Полагая (принимается любое значение), получаем:

Общее решение системы:

Этот пример может быть решен другим способом:

Продифференцируем первое уравнение:

Подставим в это выражение производную У¢ =2X + 2Y из второго уравнения.

Подставим сюда У, выраженное из первого уравнения:

Обозначив , получаем решение системы:

Пример. Найти решение системы уравнений

Эта система дифференциальных уравнений не относится к рассмотренному выше типу, т. к. не является однородным (в уравнение входит независимая переменная Х).

Для решения продифференцируем первое уравнение по Х. Получаем:

Заменяя значение Z’ из второго уравнения получаем: .

С учетом первого уравнения, получаем:

Решаем полученное дифференциальное уравнение второго порядка.

Общее решение однородного уравнения:

Теперь находим частное решение неоднородного дифференциального уравнения по формуле

Общее решение неоднородного уравнения:

Подставив полученное значение в первое уравнение системы, получаем:

Пример. Найти решение системы уравнений:

Составим характеристическое уравнение:

Если принять g = 1, то решения в этом случае получаем:

Если принять g = 1, то получаем:

Если принять g = 3, то получаем:

Общее решение имеет вид:

Элементы теории устойчивости.

Теория устойчивости решений дифференциальных уравнений является одним из разделов Качественной теории дифференциальных уравнений, которая посвящена не нахождению какого – либо решения уравнения, а изучению характера поведения этого решения при изменении начальных условий или аргумента.

Этот метод особенно важен, т. к. позволяет делать вывод о характере решения без непосредственного нахождения этого решения. Т. е. даже в тех случаях, когда решение дифференциального уравнения вообще не может быть найдено аналитически.

Пусть имеется некоторое явление, описанное системой дифференциальных уравнений:

(1)

И начальные условия:

Для конкретного явления начальные условия определяются опытным путем и поэтому неточны.

Теорема. (о непрерывной зависимости решения от начальных условий)

Если правая часть дифференциального уравнения Непрерывна и по переменной у имеет ограниченную частную производную на области прямоугольника, ограниченного , то решение

, удовлетворяющее начальным условиям , непрерывно зависит от начальных данных, т. е. для любого , при котором если

то при условии, что

где

Эта теорема справедлива как для одного дифференциального уравнения, так и для системы уравнений.

Определение. Если — решение системы дифференциальных уравнений, то это решение называется Устойчивым по Ляпунову, если для любого , такое, что для любого решения той же системы, начальные условия которого удовлетворяют неравенствам

(Ляпунов Александр Михайлович (1857 – 1918) академик Петерб. АН)

Т. е. можно сказать, что решение j(t) устойчиво по Ляпунову, если близкие к нему по начальным условиям решения остаются близкими и при T ³ T0.

Если , то решение j(t) называется Асимптотически устойчивым.

Исследование на устойчивость по Ляпунову произвольного решения системы Можно свести к исследованию на устойчивость равного нулю решения некоторой другой системы, которая получена из данной заменой неизвестных функций:

(2)

Система (2) имеет тривиальное (равное нулю) решение

Теорема. Решение системы (1) устойчиво по Ляпунову тогда и только тогда, когда устойчиво по Ляпунову тривиальное решение системы (2).

Это тривиальное решение называется Положением равновесия Или Точкой покоя.

Определение. Точка покоя Системы (2) устойчива по Ляпунову, если для любого такое, что из неравенства

.

Теорема. (Теорема Ляпунова). Пусть задана система

Имеющая тривиальное решение .

Пусть существует дифференцируемая функция , удовлетворяющая условиям:

1) ³0 и V = 0 только при у1 = у2 = … = уN =0, т. е. функция V Имеет минимум в начале координат.

2) Полная производная функции V Вдоль фазовой траектории (т. е. вдоль решения Yi(T) системы (1)) удовлетворяет условию:

при

Тогда точка покоя устойчива по Ляпунову.

Если ввести дополнительное требование, чтобы вне сколь угодно малой окрестности начала координат выполнялось условие

Где B — постоянная величина, то точка покоя асимптотически устойчива.

Функция V называется Функцией Ляпунова.

Классификация точек покоя.

Рассмотрим систему двух линейных дифференциальных уравнений с постоянными коэффициентами

Характеристическое уравнение этой системы имеет вид:

Рассмотрим следующие возможные случаи:

1) Корни характеристического уравнения действительные, отрицательные и различные.

Точка покоя будет устойчива. Такая точка покоя называется Устойчивым узлом.

2) Корни характеристического уравнения действительны и

или .

В этом случае точка покоя также будет устойчива.

3) Хотя бы один из корней положителен.

В этом случае точка покоя Неустойчива, и такую точку называют Неустойчивым седлом.

4) Оба корня характеристического уравнения положительны .

В этом случае точка покоя Неустойчива, и такую точку называют Неустойчивым узлом.

Если полученного решения Системы исключить параметр T, то полученная функция дает траекторию движения в системе координат XOY.

Возможны следующие случаи:

b b

Устойчивый узел. Неустойчивый узел. Седло.

5) Корни характеристического уравнения комплексные .

Если Р = 0, т. е. корни чисто мнимые, то точка покоя (0, 0) устойчива по Ляпунову.

Такая точка покоя называется Центром.

Если P 0, то точка покоя неустойчива и называется Неустойчивым фокусом.

Уравнения математической физики.

Уравнения в частных производных.

Определение. Дифференциальным уравнением в частных производных Называется уравнение относительно неизвестной функции нескольких переменных, ее аргументов и ее частных производных различных порядков.

Порядком Дифференциального уравнения в частных производных называется порядок старшей производной, входящей в это уравнение. Решением Уравнения будет некоторая функция , которая обращает уравнение в тождество.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Как решать систему уравнений

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Видео:Система уравнений. Метод алгебраического сложенияСкачать

Основные понятия

Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.

Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.

Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.

Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Линейное уравнение с двумя переменными

Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.

Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.

Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:

Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.

Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.

Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).

Провести прямую через эти две точки и вуаля — график готов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Система двух линейных уравнений с двумя переменными

Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.

Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:

Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.

Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.

Можно записать систему иначе:

Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.

Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.

Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.

Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Метод подстановки

Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:

Выразить одну переменную через другую из более простого уравнения системы.

Подставить то, что получилось на место этой переменной в другое уравнение системы.

Решить полученное уравнение, найти одну из переменных.

Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.

Записать ответ. Ответ принято записывать в виде пар значений (x; y).

Потренируемся решать системы линейных уравнений методом подстановки.

Пример 1

Решите систему уравнений:

x − y = 4
x + 2y = 10

Выразим x из первого уравнения:

x − y = 4
x = 4 + y

Подставим получившееся выражение во второе уравнение вместо x:

x + 2y = 10
4 + y + 2y = 10

Решим второе уравнение относительно переменной y:

4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2

Полученное значение подставим в первое уравнение вместо y и решим уравнение:

x − y = 4
x − 2 = 4
x = 4 + 2
x = 6

Ответ: (6; 2).

Пример 2

Решите систему линейных уравнений:

x + 5y = 7
3x = 4 + 2y

Сначала выразим переменную x из первого уравнения:

x + 5y = 7
x = 7 − 5y

Выражение 7 − 5y подставим вместо переменной x во второе уравнение:

3x = 4 + 2y
3 (7 − 5y) = 4 + 2y

Решим второе линейное уравнение в системе:

3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1

Подставим значение y в первое уравнение и найдем значение x:

x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2

Ответ: (2; 1).

Пример 3

Решите систему линейных уравнений:

x − 2y = 3
5x + y = 4

Из первого уравнения выразим x:

x − 2y = 3
x = 3 + 2y

Подставим 3 + 2y во второе уравнение системы и решим его:

5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1

Подставим получившееся значение в первое уравнение и решим его:

x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1

Ответ: (1; −1).

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Метод сложения

Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:

При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.

Складываем почленно левые и правые части уравнений системы.

Решаем получившееся уравнение с одной переменной.

Находим соответствующие значения второй переменной.

Запишем ответ в в виде пар значений (x; y).

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Система линейных уравнений с тремя переменными

Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:

Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).

Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.

Видео:Решение систем уравнений методом сложенияСкачать

Решение задач

Разберем примеры решения систем уравнений.

Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?

5x − 8y = 4x − 9y + 3

5x − 8y = 4x − 9y + 3

5x − 8y − 4x + 9y = 3

Задание 2. Как решать систему уравнений способом подстановки

Выразить у из первого уравнения:

Подставить полученное выражение во второе уравнение:

Найти соответствующие значения у:

Задание 3. Как решать систему уравнений методом сложения

1. Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:

1. Решаем полученное квадратное уравнение любым способом. Находим его корни:

1. Найти у, подставив найденное значение в любое уравнение:

1. Ответ: (1; 1), (1; -1).

Задание 4. Решить систему уравнений

Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.

Задание 5. Как решить систему уравнений с двумя неизвестными

При у = -2 первое уравнение не имеет решений, при у = 2 получается:

🔥 Видео

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать

Неоднородная система линейных уравненийСкачать

Как решать систему уравнений графическим методом? | Математика | TutorOnlineСкачать

Фундаментальная система решений системы линейных уравнений ФСР СЛАУСкачать

Решение систем уравнений второго порядка. 8 класс.Скачать

Решение систем уравнений методом сложенияСкачать

Решение системы уравнений методом ГауссаСкачать

Видеоурок "Системы дифференциальных уравнений"Скачать

Матричный метод решения систем уравненийСкачать