Для тех, кто подзабыл матешу
Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
- Взять все числа от 5 до 15 (снизу и сверху знака Σ).
- С каждым из этих чисел сделать то, что написано справа от Σ, — то есть умножить на два.
- Сложить результаты этих операций.
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Видео:Математика без Ху!ни. Вычисление суммы рядаСкачать

Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Видео:Что такое знак СУММЫ и как он работает?Скачать

Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
Видео:Линейные уравнения с одной переменной, содержащие переменную под знаком модуля. 6 класс.Скачать

Как найти сумму числового и функционального ряда
Числовой ряд является некой последовательностью, которая рассматривается совместно с другой последовательностью (ее еще называют последовательностью частичных сумм). Подобные понятия применяются в математическом и комплексном анализе.
Сумму числового ряда можно легко вычислить в Excel с помощью функции РЯД.СУММ. Рассмотрим на примере, как работает данная функция, а после построим график функций. Научимся применять числовой ряд на практике при подсчете роста капитала. Но для начала немного теории.
Видео:Сумма арифметических прогрессий | МатематикаСкачать

Сумма числового ряда
Числовой ряд можно рассматривать как систему приближений к числам. Для его обозначения применяют формулу:
Здесь показана начальная последовательность чисел ряда и правило суммирования:
- ∑ — математический знак суммы;
- ai — общий аргумент;
- i — переменная, правило для изменения каждого последующего аргумента;
- ∞ — знак бесконечности, «предел», до которого проводится суммирование.
Запись 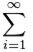
В соответствии с переменной i ряд можно записать развернуто:
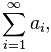
Определение суммы числового ряда дается через «частичные суммы». В математике они обозначаются Sn. Распишем наш числовой ряд в виде частичных сумм:
Сумма числового ряда – это предел частичных сумм Sn. Если предел конечен, говорят о «сходящемся» ряде. Бесконечен – о «расходящемся».
Сначала найдем сумму числового ряда:
Теперь построим в Excel таблицу значений членов ряда:
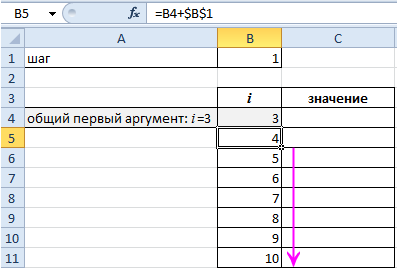
Общий первый аргумент берем из формулы: i=3.
Все следующие значения i находим по формуле: =B4+$B$1. Ставим курсор в нижний правый угол ячейки В5 и размножаем формулу.
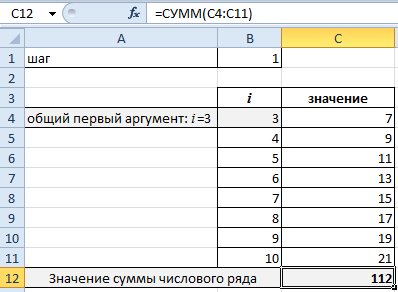
Найдем значения. Делаем активной ячейку С4 и вводим формулу: =СУММ(2*B4+1). Копируем ячейку С4 на заданный диапазон.
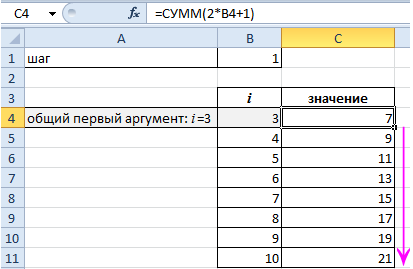
Значение суммы аргументов получаем с помощью функции: =СУММ(C4:C11). Комбинация горячих клавиш ALT+«+» (плюс на клавиатуре).
Видео:Решить уравнения, используя формулы сокращенного умножения.Сумма и квадрат разности. Алгебра 7 классСкачать

Функция РЯД.СУММ в Excel
Для нахождения суммы числового ряда в Excel применяется математическая функция РЯД.СУММ. Программой используется следующая формула:
- х – значение переменной;
- n – степень для первого аргумента;
- m – шаг, на который увеличивается степень для каждого последующего члена;
- а – коэффициенты при соответствующих степенях х.
Важные условия для работоспособности функции:
- все аргументы обязательные (то есть все должны быть заполнены);
- все аргументы – ЧИСЛОвые значения;
- вектор коэффициентов имеет фиксированную длину (предел в «бесконечность» не подойдет);
- количество «коэффициентов» = числу аргументов.
Видео:ЕГЭ по Математике. Занятие №16Скачать

Вычисление суммы ряда в Excel
Та же функция РЯД.СУММ работает со степенными рядами (одним из вариантов функциональных рядов). В отличие от числовых, их аргументы являются функциями.
Функциональные ряды часто используются в финансово-экономической сфере. Можно сказать, это их прикладная область.
Например, положили в банк определенную сумму денег (а) на определенный период (n). Имеем ежегодную выплату х процентов. Для расчета наращенной суммы на конец первого периода используется формула:
На конец второго и последующих периодов – вид выражений следующий:
S2 = a (1 + x) 2 ; S3 = a (1 + x) 2 и т.д.
Чтобы найти общую сумму:
Sn = a (1 + x) + a (1 + x) 2 + a (1 + x) 3 + … + a (1 + x) n
Частичные суммы в Excel можно найти с помощью функции БС().
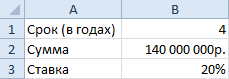
Исходные параметры для учебной задачи:
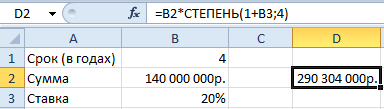
Используя стандартную математическую функцию, найдем накопленную сумму в конце срока сумму. Для этого в ячейке D2 используем формулу: =B2*СТЕПЕНЬ(1+B3;4)
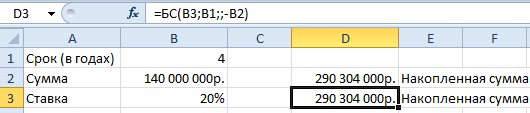
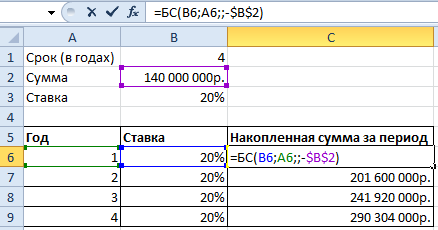
Теперь в ячейке D3 решим эту же задачу с помощью встроенной функции Excel: =БС(B3;B1;;-B2)
Результаты одинаковые, как и должно быть.
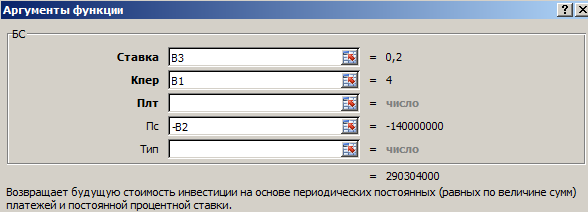
Как заполнить аргументы функции БС():
- «Ставка» — процентная ставка, под которую оформлен вклад. Так как в ячейке В3 установлен процентный формат, мы в поле аргумента просто указали ссылку на эту ячейку. Если было бы указано число, то прописывали бы его сотую долю (20/100).
- «Кпер» — число периодов для выплат процентов. В нашем примере – 4 года.
- «Плт» — периодические выплаты. В нашем случае их нет. Поэтому поле аргумента не заполняем.
- «Пс» — «приведенная стоимость», сумма вклада. Так как мы на время расстаемся с этими деньгами, параметр указываем со знаком «-».
Таким образом, функция БС помогла найти нам сумму функционального ряда.
В Excel есть и другие встроенные функции для нахождения разных параметров. Обычно это функции для работы с инвестиционными проектами, ценными бумагами и амортизационными платежами.
Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Построение графика функций суммы числового ряда
Построим график функций, отражающий рост капитала. Для этого нам нужно построить график функции являющейся суммой построенного ряда. За пример, возьмем те же данные по вкладу:
Дальше нам нужна функция для начисления сложных процентов — БС(). Мы узнаем будущею стоимость инвестиций при условии равных платежей и постоянной процентной ставке. Используя функцию БС(), заполним таблицу:
В первой строке показана накопленная сумма через год. Во второй – через два. И так далее.
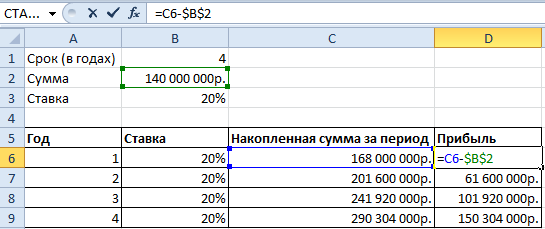
Сделаем еще один столбец, в котором отразим прибыль:
Как мы считали – в строке формул.
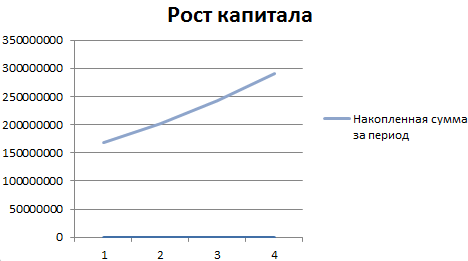
На основании полученных данных построим график функций.
Выделим 2 диапазона: A5:A9 и C5:C9. Переходим на вкладку «Вставка» — инструмент «Диаграммы». Выбираем первый график:
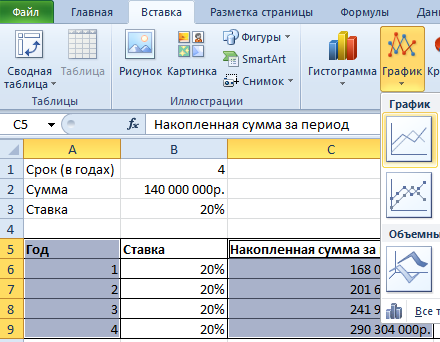
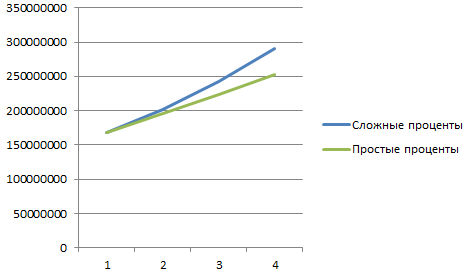
Сделаем задачу еще более «прикладной». В примере мы использовали сложные проценты. Они начисляются на наращенную в предыдущем периоде сумму.
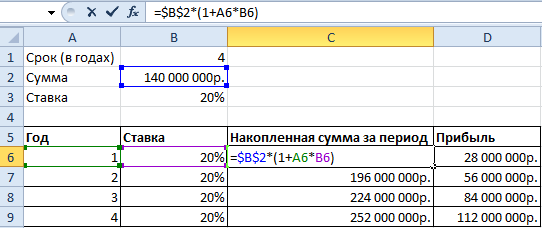
Возьмем для сравнения простые проценты. Формула простых процентов в Excel: =$B$2*(1+A6*B6)
Добавим полученные значения в график «Рост капитала».
Какие именно выводы сделает инвестор – очевидно.
Математическая формула частичной суммы функционального ряда (с простыми процентами): Sn = a (1 + x*n), где а – первоначальная сумма вклада, х – проценты, n – период.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Сумма ряда
Содержание:
Понятие суммы ряда
Постановка задачи. Найти сумму ряда
где 
План решения. Суммой ряда 


где
1. По условию задачи
Если корни знаменателя различаются на целое число, т.е. 




По этой ссылке вы найдёте полный курс лекций по высшей математике:
2. Разлагаем общий член ряда на элементарные дроби:
и выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичных сумм ряда.
3. Находим 

сократив соответствующие слагаемые.
4. Вычисляем сумму ряда по формуле (1)
и записываем ответ.
Пример:
Найти сумму ряда
Решение:
1. Корни знаменателя 




2. Разлагаем общий член ряда на элементарные дроби
и выписываем несколько членов ряда:
3. Сокращая все слагаемые, какие возможно, находим 
4. Вычисляем сумму ряда по формуле (1):
Ответ:
Возможно вам будут полезны данные страницы:
Вычисление суммы ряда почленным интегрированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
План решения.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
с областью сходимости 
3. Известна формула для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
Заметим, что так как ряд (1) сходится в граничной точке 
6. Вычисляем интеграл, делаем замену 

Замечание. Если ряд имеет вид
то применяем теорему о почленном интегрировании степенного ряда дважды или разлагаем дробь на элементарные:
и вычисляем сумму каждого ряда почленным интегрированием.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
В граничных точках при 


Следовательно, данный ряд сходится при всех 
2. Сделаем замену 
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке 
Заметим, что так как ряд (1) сходится в граничной точке 

6. Заменяя 

Ответ.
Вычисление суммы ряда почленным дифференцированием
Постановка задачи. Найти сумму функционального ряда вида
и указать область сходимости ряда к этой сумме.
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством
Если 

2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов

3. Известна формула для суммы членов бесконечно убывающей геометрической прогрессии
4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (1), получаем
6. Вычисляем производную и делаем замену 

Замечание. Если ряд имеет вид
то вычисляем сумму трех рядов, причем при вычислении суммы ряда
применяем теорему о почленном дифференцировании степенного ряда дважды.
Пример:
Найти сумму ряда
и указать область сходимости ряда к этой сумме.
Решение:
1. Находим область сходимости ряда.
По признаку Коши интервал сходимости определяется неравенством 



2. Делаем в исходном ряде замену 
Следовательно, достаточно найти суммы рядов
3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии:
Следовательно, 

4. Кроме того, имеем очевидное равенство
5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (2), получаем
Заменяя 

Ответ.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
📸 Видео
Найти значение суммы и произведения корней квадратного уравненияСкачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Сумма числового ряда n^2/2^nСкачать

Квадрат суммы и квадрат разности двух выражений. 7 класс.Скачать

СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Уравнения с модулем. Что такое модуль числа. Алгебра 7 класс.Скачать

Уравнения с модулемСкачать

Решение уравнений. Как переносить слагаемые из одной части уравнения в другую. Математика 6 классСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

РЕШЕНИЕ УРАВНЕНИЙ |ПОДРОБНОЕ ОБЪЯСНЕНИЕ КАК РЕШИТЬ УРАВНЕНИЯ / ПРОСТЫЕ УРАВНЕНИЯ 2 КЛАСС МАТЕМАТИКАСкачать

Решение уравнений, 6 классСкачать






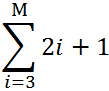
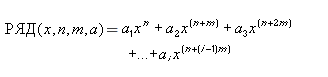




















 , целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем
, целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем

































