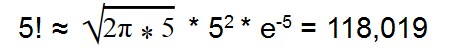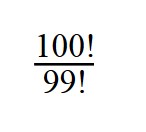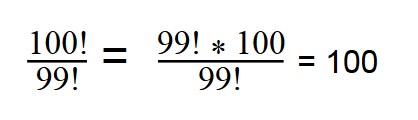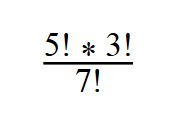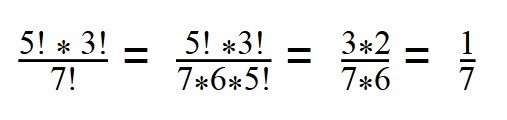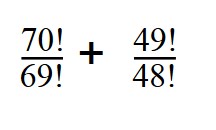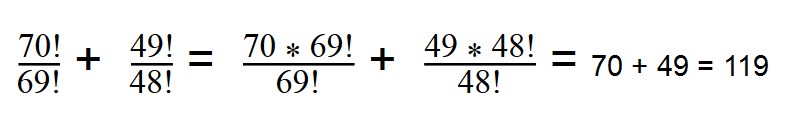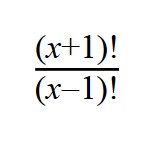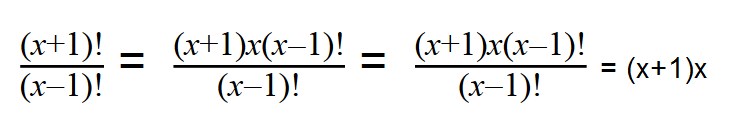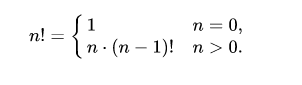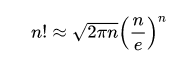О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Факториал: определение
- Формулы и свойства факториала
- Примеры решений
- Что означает восклицательный знак в математике? + Пример — 2022 — Go Homework
- Ответ:
- Объяснение:
- Что означает разрыв в математике? + Пример
- Что означает частное в математике? + Пример
- Что такое взаимность в математике? + Пример
- Факториал — формула, свойства и примеры решений
- Таблица факториалов
- Свойства факториалов
- Рекуррентная формула
- Комбинаторная интерпретация
- Формула Стирлинга
- Расчет по предыдущему значению
- Некоторые очень большие значения
- 🌟 Видео
Видео:Факториалы — это легко! Показываю, что это такое и как решать этот примерСкачать

Факториал: определение
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».
Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:
Число должно быть целое и положительное:
- 3! 56! 12!
| Формула факториала n!=1⋅2⋅3⋅. ⋅(n−2)⋅(n−1)⋅n |
Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.
Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6
Видео:ФакториалСкачать

Формулы и свойства факториала
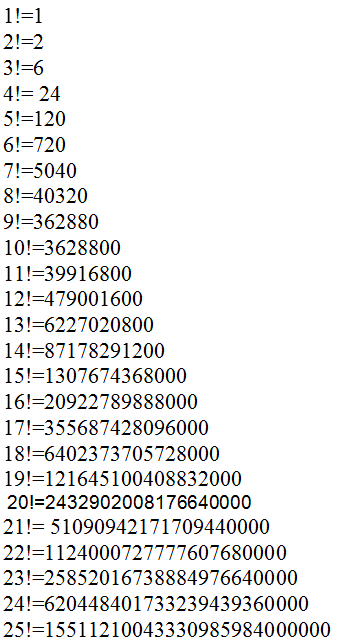
Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| 8! = 40320 |
| 9! = 362880 |
| 10! = 3628800 |
| 11! = 39916800 |
| 12! = 479001600 |
| 13! = 6227020800 |
| 14! = 87178291200 |
| 15! = 1307674368000 |
| 16! = 20922789888000 |
| 17! = 355687428096000 |
| 18! = 6402373705728000 |
| 19! = 121645100408832000 |
| 20! = 2432902008176640000 |
| 21! = 51090942171709440000 |
| 22! = 1124000727777607680000 |
| 23! = 25852016738884976640000 |
| 24! = 620448401733239439360000 |
| 25! = 15511210043330985984000000 |
Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:
- (n — 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)
- n! = 1*2*3*4*5*. *(n — 2)(n — 1)n
- (n + 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)n(n + 1)
С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.
Такая формула дает результат с небольшой погрешностью.
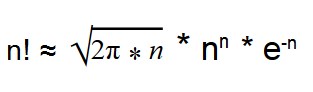 |
Рекуррентная формула
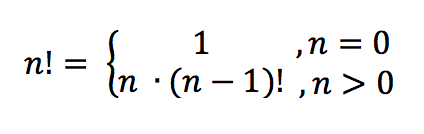 |
- 5! = 5*(5 — 1)! = 5*4! = 5*24 = 120
- 6! = 6*(6-1)! = 6*5! = 6*120 = 720
Для решения примеров обращайтесь к таблице.
Примеры умножения факториалов:
- Пользуйтесь готовой таблицей 5! * 7! = 120 * 5040 = 604800
- Или раскладывайте факториалы отдельно, если хотите потренироваться:
5! = 1*2*3*4*5 = 4! * 5 =120
7! = 1*2*3*4*5*6*7 = 6! * 7 = 5040
120 * 5040 = 604800
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Видео:Что такое факториал | МатематикаСкачать

Примеры решений
Давайте поупражняемся и решим пару примеров.
1. Сократите дробь:
При сокращении факториалов, пользуйтесь свойством:
n! = (n — 1)! * n
100! = 99! * 100
Далее сокращаем по принципу сокращения обыкновенных дробей.
2. Вычислите значение выражения с факториалом: 8! + 5!
Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.
А можно потренироваться и разложить их:
8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440
3. Вычислите значение выражения:
7! = 1*2*3*4*5*6*7 = 5! * 6 *7
Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.
4. Вычислите значение выражение:
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*. *69 = 69! * 70
49! = 1*2*3*. 49! * 48
Далее сокращаем все одинаковые множители.
5. Сократите дробь:
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.
Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.
Видео:14. Вычисление пределов последовательностей ( предел с факториалом ), примеры 7, 8.Скачать

Что означает восклицательный знак в математике? + Пример — 2022 — Go Homework
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Ответ:
Восклицательный знак обозначает то, что называется факториал.
Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Объяснение:
Формальное определение #n #! (n факториал) — произведение всех натуральных чисел, меньших или равных # П # , В математических символах:
#n! = n * (n-1) * (n-2) … #
Поверь мне, это менее запутанно, чем кажется. Скажи, что ты хотел найти #5!# , Вы просто умножаете все числа, меньшие или равные #5# пока вы не доберетесь до #1# :
#5! = 5*4*3*2*1=120#
Или же #6!# :
#6! = 6*5*4*3*2*1=720#
Самое замечательное в факториалах — это то, как легко вы можете их упростить. Допустим, вы получили следующую проблему:
вычисление #(10!)/(9!)# .
Исходя из того, что я сказал вам выше, вы можете подумать, что вам нужно будет умножить #10*9*8*7…# и разделить его на #9*8*7*6…# что, вероятно, займет много времени. Тем не менее, это не должно быть так сложно. поскольку #10! = 10*9*8*7*6*5*4*3*2*1# , а также #9! = 9*8*7*6*5*4*3*2*1# Вы можете выразить проблему следующим образом:
#(10*9*8*7*6*5*4*3*2*1)/(9*8*7*6*5*4*3*2*1)#
И посмотрите на это! Число #1# через #9# отменить:
# (10 * cancel9 * cancel8 * cancel7 * cancel6 * cancel5 * cancel4 * cancel3 * cancel2 * cancel1) / (cancel9 * cancel8 * cancel7 * cancel6 * cancel5 * cancel4 * cancel3 * cancel2 * cancel1) #
Оставив нас с #10# в результате.
Кстати, #0! = 1# , Чтобы узнать почему, проверьте эту ссылку.
Приложения Факториалов
Место, где факториалы действительно полезны, — это вероятность. Например: сколько слов вы можете сделать из букв # ABCDE # , не повторяя ни одной буквы? (Слова в этом случае не должны иметь смысла — вы можете иметь # AEDCB # , например).
Ну у вас есть #5# выбор для вашего первого письма, #4# для вашего следующего письма (помните — без повторов; если вы выбрали # A # для вашего первого письма, вы можете выбрать только # BCDE # для вашего второго), #3# для следующего, #2# для одного после этого, и #1# за последний. Правила вероятности говорят, что общее количество слов является продуктом выбора:
#underbrace (5) _ («выбор по первой букве») * 4 * 3 * 2 * 1 #
И четыре — это количество вариантов для второй буквы и так далее. Но подождите — мы узнаем это, верно! Это #5!# :
#5! = 5*4*3*2*1=120#
Так что есть #120# пути.
Вы также увидите факториалы, используемые в перестановки а также комбинации , что также связано с вероятностью. Символ для перестановок #»_энергетический ядерный реактор# и символ для комбинаций # «_ NC_r # (люди используют # ((П), (г)) # для комбинаций большую часть времени, и вы говорите «n выбирают r».) Формулы для них:
# «_ NP_r = (п!) / ((П-т)!) #
# «_ NC_r = (п!) / ((П-р)! Г!) #
Там мы видим нашего друга, факториала. Объяснение перестановок и комбинаций сделает этот длинный ответ еще длиннее, поэтому просмотрите эту ссылку для перестановок и эту ссылку для комбинаций.
Видео:Решение неравенства методом интерваловСкачать

Что означает разрыв в математике? + Пример
Функция имеет разрыв, если она не определена для определенного значения (или значений); Есть 3 типа разрыва: бесконечный, точечный и скачкообразный. Многие общие функции имеют один или несколько разрывов. Например, функция y = 1 / x не является четко определенной для x = 0, поэтому мы говорим, что она имеет разрыв для этого значения x. Смотрите график ниже. Обратите внимание, что там кривая не пересекается при x = 0. Другими словами, функция y = 1 / x не имеет значения y для x = 0. Аналогично, периодическая функция y = tanx имеет разрывы при x = pi / 2, (3pi) / 2, (5pi) / 2 . В рациональных функциях возникают бесконечные
Видео:Факториал FactorialСкачать

Что означает частное в математике? + Пример
Увидеть ниже. Частное является результатом деления. Пример: 10/5 = 2 color (white) (8888) 2 — это частное 25/5 = 5color (white) (8888) 5 — это частное и т. Д .:
Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Что такое взаимность в математике? + Пример
В общем, взаимные средства (i) обратно соотносятся (ii) разделяются, ощущаются или проявляются обеими сторонами (iii) взаимно соответствующие ответы, такие как улыбка для улыбки. Математическое взаимное имеет четкое определение. По отношению к количеству это 1 / (количество). Относительно действительного или комплексного числа x, обратное значение равно 1 / x. Например, каждое из 5 и 1/5 является обратной величиной другого. Символически обратное значение x записывается в алгебре как x ^ (- 1). Пожалуйста, не смешивайте это с обратной операцией для операции f. Конечно, xx ^ (- 1) = x ^ (- 1) = 1 (количество), но, напротив,
Видео:Страница 81 Задание внизу – Математика 2 класс (Моро) Часть 1Скачать

Факториал — формула, свойства и примеры решений
Факториал числа n – это произведение чисел от 1 до n. Определён только для целых неотрицательных чисел. Формула факториала:
Математическая формула представлена восклицательным знаком «!». Термин был введен в 1800 году, а обозначение появилось только в 1808. В формуле нужно умножить все целые числа от 1 до значения самого числа, стоящего под знаком факториала.
Это очень просто, вот пример:
7! = 1 * … * 7 = 5040.
Факторизация — разложение функции на множители.
Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Таблица факториалов
Видео:Почему: 0!=1? ★ Почему факториал нуля равен единице?Скачать

Свойства факториалов
Рекуррентная формула
Комбинаторная интерпретация
Функция n может интерпретироваться как количество перестановок. К примеру, для 3-х элементов есть 3! = 6 перестановки.
Формула Стирлинга
Позволяет не перемножать большие числа. Обычно необходим только главный член:
Можно ли вычислить 0,5 или -3,217? Нет, нельзя. Но можно использовать нечто под названием «Гамма-функция», что намного сложнее.
Расчет по предыдущему значению
Функцию легко вычислить из предыдущего значения:
А как вычислить факториал нуля? Если вернуться к определению, то видно, что применять его в случае «0» нет смысла. Положительных чисел до 0 нет, поэтому 0 x 0 = 0.
Однако было решено, что в случае 0 результат будет равен 1.
Некоторые очень большие значения
Онлайн калькулятор поможет сделать вычисление – всего лишь надо найти знак, похожий на «x!» или «n!». Нужно обратить внимание, что браузеры могут испытывать затруднения при попытке отобразить более крупные числа и может произойти сбой.
Некоторые браузеры могут не позволять копировать, поэтому необходимо будет загрузить большие результаты в виде текстового файла.
Примеры вычисления факториалов больших чисел:
70! приблизительно 1 19785716669969869891796072783721 x 10100, что немного больше, чем «гуголь» (1 и 100 нулей);
100! это примерно 9 33262154444944152681699238856 x 101576 x 10157;
200! это примерно 7 88657867867364479050355236321393 x 103743.
Как найти функцию в Паскаль? Вычисление легко реализуется на разных языках программирования. Можно выбрать два метода: итеративный, то есть он создает цикл, в котором временная переменная умножается на каждое натуральное число от 1 до n, или рекурсивный, в котором функция вызывает себя до достижения базового варианта 0! = 1.
Программа на языке Паскаль:
На языке Си вычисления делаются с помощью рекурсивной функции. Следует заметить, что если начать вычислять факториал отрицательного числа в неаккуратно написанной функции, то это приведет к зацикливанию.
Факториал дроби (½) — это половина квадратного корня pi = (½)√π.
🌟 Видео
Как решать неравенства? Часть 1| МатематикаСкачать

Что такое знак СУММЫ и как он работает?Скачать

Математика | Как решать уравнения с модулем?Скачать

ВЫУЧИ ЭТО и получишь 5-ку по Алгебре — Алгебра для чайниковСкачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Алгебра 9. Урок 7 - Неравенства. Метод интервалов - основные фактыСкачать

Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать

Решение квадратных неравенств | МатематикаСкачать