Как решить уравнение с lim (3 видео) | Про уравнения

Что такое предел функции

В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами.

Содержание

Определение предела функции
Решение пределов
С заданным числом
С бесконечностью
С неопределенностью (икс стремится к бесконечности)
С неопределенностью (икс стремится к конкретному числу)
Что означает предел в математике
Что такое предел в математике
График и предел
Пределы в жизни
Погрешность в пределах
Считаем предел в программировании
Предел функции.
Предел функции по Гейне.
Предел функции по Коши.
Решение пределов функции.
📺 Видео

Видео:Предел функции на бесконечности. 10 класс.Скачать

Определение предела функции

Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.

Запись предела:

предел обозначается значком lim;
под ним добавляется, к какому значению стремится аргумент (переменная) функции. Обычно, это x , но не обязательно, например: “ x →1″;

Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):

Читается как “предел функции при икс, стремящемся к единице”.

x →1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут).

Видео:Матан. Пределы для успешной сдачи зачёта | TutorOnline МатематикаСкачать

Решение пределов

С заданным числом

Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x →1):

Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу).

С бесконечностью

В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например:

Если x →∞, то заданная функция стремится к минус бесконечности (-∞), т.к.:

3 – 1 = 2
3 – 10 = -7
3 – 100 = -97
3 – 1000 – 997 и т.д.

Другой более сложный пример

Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом.

Таким образом при “икс”, стремящемся к бесконечности, функция неограниченно растет.

С неопределенностью (икс стремится к бесконечности)

В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности.

Пример: давайте вычислим предел ниже.

Выражения и в числителе, и а знаменателе стремятся к бесконечности. Можно предположить, что в таком случае решение будет таким:

Однако не все так просто. Чтобы решить предел нам нужно сделать следующее:

1. Находим x в старшей степени для числителя (в нашем случае – это два).

2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).

3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень.

4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2.

С неопределенностью (икс стремится к конкретному числу)

И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности.

В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль.

Пример: Найдем предел функции ниже.

1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида.

2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.

В нашем случаем корнями выражения в числителе () являются числа 1 и 1,5. Следовательно его можно представить в виде: .

Знаменатель () изначально является простым.

3. Получаем вот такой видоизмененный предел:

4. Дробь можно сократить на ():

5. Остается только подставить число 1 в выражение, получившееся под пределом:

Видео:27. Вычисление предела функции №1. Примеры 1-4Скачать

Что означает предел в математике

Сага о погрешностях при участии слова lim

Кто о чём, а мы продолжаем разбирать сложную математику, чтобы она не была такой сложной.

Видео:36. Вычисление пределов функций с использованием 2-го замечательного пределаСкачать

Что такое предел в математике

Когда математики говорят о пределах, то имеют в виду такую последовательность событий:

Есть функция — это просто какая-то «коробка» с математикой. Ты ей на вход число, она его обрабатывает у себя внутри и отдаёт другое число.
У функции есть как минимум два числа: то, которое ты ей даёшь на вход; и то, которое получаешь на выходе.
Иногда математикам интересно, что будет, если число на входе будет к чему-то стремиться. А именно: «Если число на входе будет стремиться вот сюда, куда будет стремиться число на выходе?»

Самое простое объяснение функции в математике.

👉 Стремиться — значит стараться приблизиться к какому-то числу, но не достигнуть его.

Если мы говорим, что переменная функции стремится к бесконечности, то это значит, что с каждым новым вычислением мы берём значение переменной больше предыдущего.

1, 2, 3, … 1000000000000003, 1000000000000004 и так до бесконечности

Наоборот тоже работает: если переменная функции стремится к нулю, то это значит, что она постоянно уменьшается:

1, 0.1, 0.01, 0.001, … 0.00000000000000000000000001 и с каждым разом число будет ближе к нулю, но никогда его не достигнет.

Стремление переменной к числу обозначается стрелкой: x→0, а предел — словом lim:

Видео:28. Вычисление пределов функций №2. Неопределенность 0/0, заданная отношением двух многочленов.Скачать

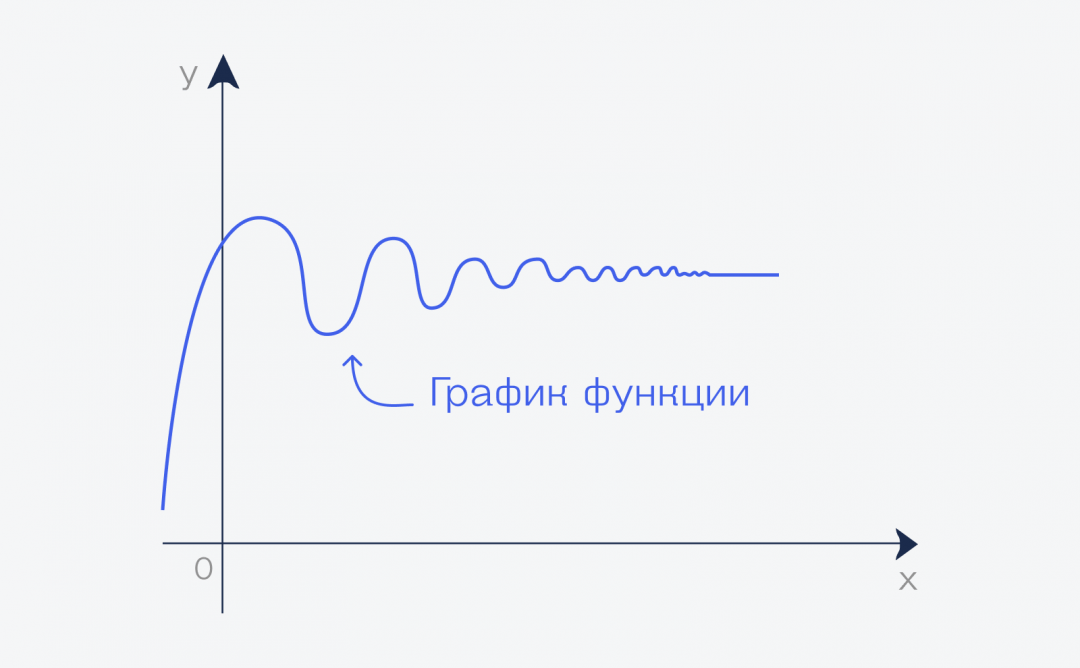
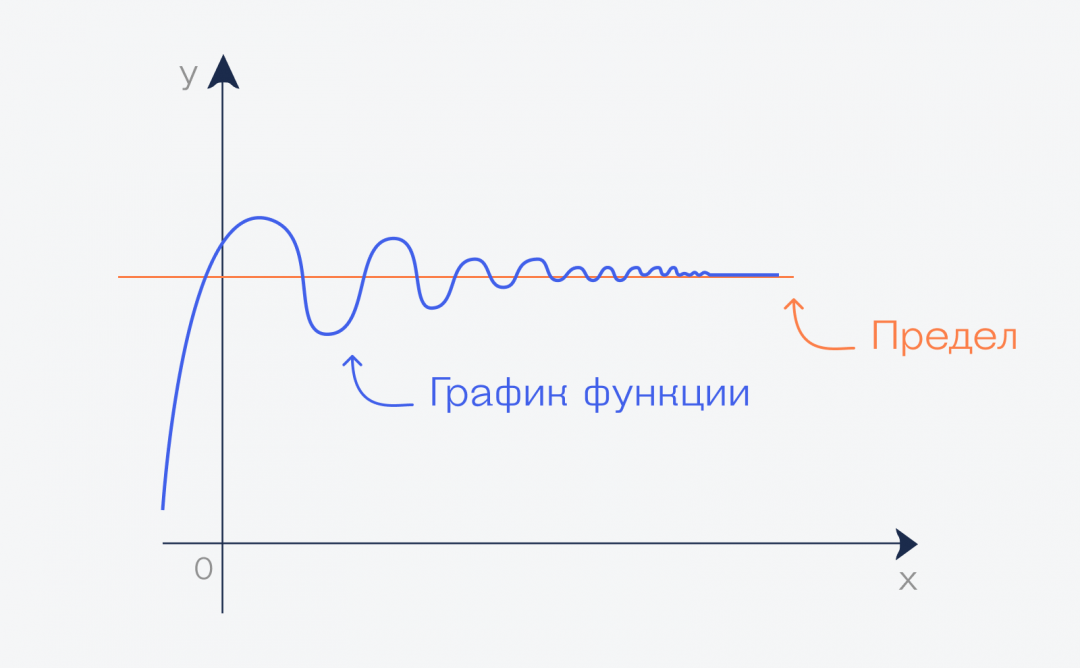
График и предел

Если мы нарисуем график этой функции, то можем увидеть, что начиная с какого-то момента он превратится в почти прямую линию вдоль оси. Почти прямую — потому что прямой он никогда не станет, но стремится к этому, если продолжить рисовать график бесконечно.

Но бесконечный график означает, что у нас переменная функции стремится к бесконечности. А значение этой линии на графике — это и есть предел этой функции при переменной, стремящейся к бесконечности:

Видео:Математика без Ху!ни. Пределы, часть1. Неопределенность, раскрытие неопределенностей.Скачать

Пределы в жизни

Пределы из математики часто используются для решения практических задач, где нужно найти точку, после которой разница в результате будет уже незаметна.

Например, бригада монтажников строит мост, и им нужно понять, какой максимальной длины можно сделать плиту перекрытия. Есть требования, что плита должна выдерживать в середине нагрузку в 50 тонн — она может быть и прочнее, но 50 тонн это минимум. Для решения этой задачи используют предел — он покажет, длиннее какого размера делать плиту нельзя, а всё, что короче, даст необходимую прочность.

Астрономы с помощью пределов изучают законы Вселенной, физики проверяют всё на прочность, и даже в микроэлектронике затухание сигналов тоже зависит от пределов функций.

Видео:Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

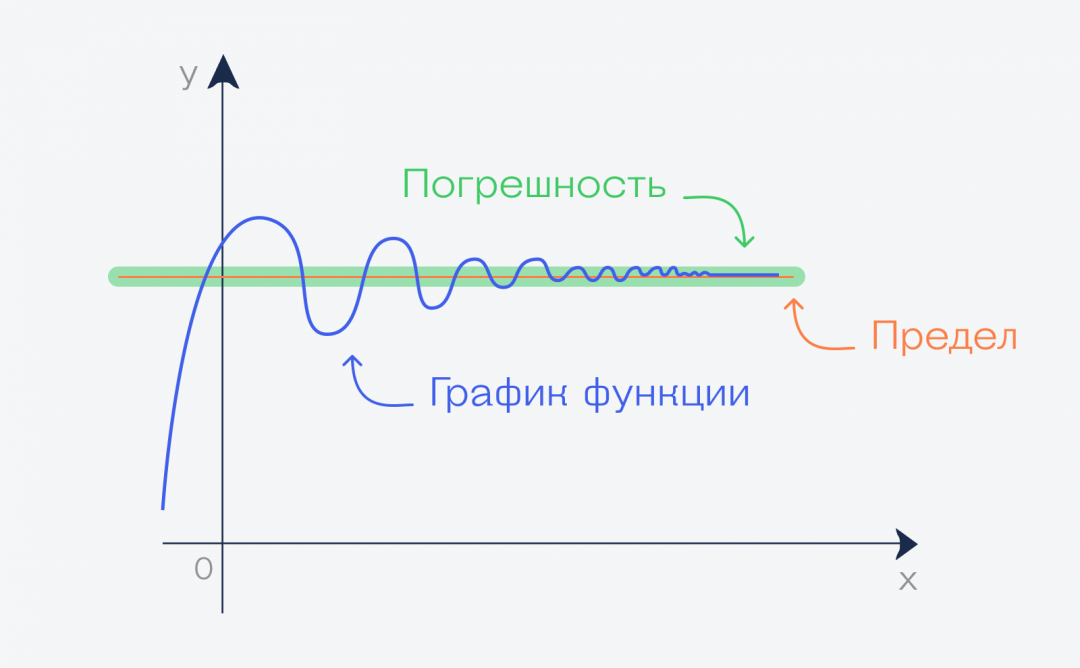
Погрешность в пределах

В математике пределы считаются точно: используются специальные формулы и трюки, которые помогают найти точный ответ. Но в жизни такая точность необязательна: можно взять любое решение, которое нас устроит с приемлемой погрешностью.

Эта погрешность поможет нам считать пределы, не зная точных математических формул подсчёта.

Видео:33. Вычисление пределов функций. Первый замечательный пределСкачать

Считаем предел в программировании

Раз у нас есть постоянное действие по уменьшению или увеличению переменной, то логично сделать из этого простой цикл и поручить его машине. Единственное, что нам нужно предусмотреть, — момент, когда цикл должен остановиться, потому что в мире математики lim по умолчанию касается бесконечности (потому что стремиться можно бесконечно).

Так как мы не знаем заранее точного предела функции, но можем контролировать количество повторений, то сделаем такие условия для остановки цикла:

Закончилось количество повторений. Например, мы заранее говорим, что будем стремиться к границе предела 10000000000 раз, но если ничего не выйдет — остановимся.
Если достигли нужной погрешности. Два соседних результата отличаются на величину погрешности или меньше — отлично, мы нашли то, что нужно.

Самый сложный момент в коде — описать то, как переменная функции к чему-то стремится. Если к бесконечности, то всё просто: на каждом шаге прибавляем или умножаем на какое-то число. А если нужно, чтобы переменная стремилась к нулю или другому числу, то можно действовать так: брать начальное число, конечное, складывать их и делить пополам. Так мы будем постоянно приближаться к нужному нам числу, но никогда его не достигнем.

⚠️ Важная оговорка: числа в компьютере — это не числа в абстрактном математическом понимании, а конечный набор данных. Конечный он тем, что на всякое число выделяется какое-то количество «клеток», в которые это число можно записать. Если у нас ограниченное количество «клеток», значит, у нас есть какой-то предел самого большого и самого малого числа.

Например, если мы дали переменной 32 бита памяти, самое малое число, которое мы сможем в нее записать, — 1,4012985 × 10 -45 . Это кажется бесконечно малым, но на самом деле, если циклически делить число на 2 несколько сотен раз в секунду, мы упремся в этот лимит точности почти сразу. Потом знаки после запятой закончатся и число очень быстро превратится в 0.

С точки зрения математики любое число можно бесконечно делить и получать бесконечное число знаков после запятой; а с точки зрения компьютера бесконечное число знаков невозможно, и если делить достаточно долго — мы получим ноль.

Поэтому в работе с пределами важно указывать либо число шагов для определения предела, либо погрешность.

Теперь напишем простой цикл, который нам посчитает lim x→2 (8−2x) / (x²−4x−12):

предел функции f(x) = (8−2x) / (x²−4x-12);
при x стремящемся к 2.

Если мы посчитаем этот предел как математики, то получим значение −1. Проверим, как с этим справится наш код:

Программа справилась и выдала результат с нужной нам точностью

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Предел функции.

Предел функции – число a будет пределом некоторой изменяемой величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.

Или другими словами, число A является пределом функции y = f (x) в точке x₀, если для всякой последовательности точек из области определения функции, не равных x₀, и которая сходится к точке x₀ (lim x_n = x0), последовательность соответствующих значений функции сходится к числу A.

График функции, предел которой при аргументе, который стремится к бесконечности, равен L:

Предел функции по Гейне.

Значение А является пределом (предельным значением) функции f (x) в точке x₀ в случае, если для всякой последовательности точек , которая сходится к x₀, но которая не содержит x₀ как один из своих элементов (т.е. в проколотой окрестности x₀), последовательность значений функции сходится к A.

Предел функции по Коши.

Значение A будет являться пределом функции f (x) в точке x₀ в случае, если для всякого вперёд взятого неотрицательного числа ε будет найдено соответствующее ему неотрицательно число δ = δ(ε) такое, что для каждого аргумента x, удовлетворяющего условию 0 3 , выносим в числителе и знаменателе его за скобки и далее сокращаем на него:

Ответ

Необходимо рассчитать предел

Первым шагом в нахождении этого предела, подставим значение 1 вместо x, в результате чего имеем неопределенность . Для её решения разложим числитель на множители, сделаем это методом нахождения корней квадратного уравнения x 2 + 2x — 3:

Таким образом, числитель будет таким:

Далее сокращаем числитель и знаменатель на (x – 1):

Ответ

Видео:29. Вычисление пределов функции №4. Неопределенность 0/0 с корнями.Скачать

Решение пределов функции.

Решение пределов функции — это определение его конкретного значения или определенной области, куда попадает функция, которая ограничена пределом.

Чтобы решить пределы, следуйте правилам:

Пробуем подставить в функцию число, результат решения и будет ответом.
Если х стремится не к числу, например в пределах вида или , то такие пределы решаются сразу, так как число, деленное на бесконечность, всегда дает 0, а деленное на нуль это и есть ∞. Если вам сложно понять саму суть бесконечности и нуля в пределах, то подставляйте вместо ∞ — бесконечно большое число – к примеру 1000 000, либо вместо нуля — бесконечно малое — например 0,000001 и после этого можете предположить к чему стремится ответ.
Существует группа пределов, в которых и в числитель, и в знаменатель при подстановке получаем либо нуль либо ∞. Это т.н. пределы с неопределенностью, часть из которых замечательные.