Биквадратные уравнения относятся к разделу школьной алгебры. Метод решения таких уравнений довольно простой, нужно использовать замену переменной.
Рассмотрим алгоритм решения:
-Что такое биквадратное уравнение?
-Как решить биквадратное уравнение?
-Метод замены переменной.
-Примеры биквадратного уравнения.
-Нахождение корней биквадратного уравнения.
- Формула биквадратного уравнения:
- Как решаются биквадратные уравнения?
- Урок 1. Биквадратные уравнения. Замена переменной в уравнениях. Алгебра 8 класс.
- Урок 2. Биквадратные уравнения. Замена переменной в уравнениях. Алгебра 8 класс.
- Урок 3. Замена переменной. Решение уравнений, приводящихся к квадратным. Алгебра 8 класс.
- Урок 4. Замена переменной в уравнениях, приводящихся к квадратным.
- Решение уравнений, сводящихся к квадратным
- Биквадратные уравнения
- Метод разложения на множители
- Метод замены переменной
- Выделение полного квадрата
- Примеры
- 🔍 Видео
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Формула биквадратного уравнения:
Формулы биквадратного уравнения отличается от квадратного уравнения тем, что у переменной х степени повышатся в два раза.
ax 4 +bx 2 +c=0, где a≠0
Видео:БИКВАДРАТНОЕ УРАВНЕНИЕ В ЕГЭ #shorts #математика #егэ2022 #огэ2021 #уравнениеСкачать

Как решаются биквадратные уравнения?
Решение биквадратных уравнений сводится сначала к замене, а потом решению квадратного уравнения:
(x^=t,;tgeq0)
t должно быть положительным числом или равным нулю
Получаем квадратное уравнение и решаем его:
at 2 +bt+c=0,
где x и t — переменная,
a, b, c -числовые коэффициенты.
(t^-5t+6=0)
Получилось полное квадратное уравнение, решаем его через дискриминант:
(D=b^-4ac=(-5)^-4times1times6=25-24=1)
Дискриминант больше нуля, следовательно, два корня, найдем их:
Возвращаемся в замену, подставим вместо переменной t полученные числа: (x^=3)
Чтобы решить такого вида уравнение, необходимо обе части уравнения занести под квадратный корень.
Получилось полное квадратное уравнение, решаем через дискриминант:
(D=b^-4ac=(-4)^-4times1times4=16-16=0)
Дискриминант равен нулю, следовательно, один корень, найдем его:
(t=frac=frac=2)
Возвращаемся в замену, подставим вместо переменной t полученное число:
Можно не во всех случаях делать замену. Рассмотрим пример.
Пример №3:
Решить биквадратное уравнение.
Выносим переменную x 2 за скобку,
Приравниваем каждый множитель к нулю
Делим всё уравнение на -4:
Чтобы решить (x^=4) такое уравнение, необходимо, обе части уравнения занести под квадратный корень.
(begin
&x^=4\
&x_=2\
&x_=-2\
end)
Пример №4:
Решите биквадратное уравнение.
(x^-16=0)
Возвращаемся в замену, подставим вместо переменной t полученное число:
(begin
&x^=4\
&x_=2\
&x_=-2
end)
Ответ: решения нет.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Видео:5 Лайфхаков Которые Помогут Решить Биквадратное УравнениеСкачать

Урок 1. Биквадратные уравнения. Замена переменной в уравнениях. Алгебра 8 класс.
Решение уравнений, приводящихся к квадратным. Биквадратные уравнения. Замена переменной в уравнениях. Какое уравнение является биквадратным. Определение биквадратного уравнения. Как решать биквадратное уравнение. Как найти корни биквадратного уравнения. Уравнения, приводящиеся к квадратным путем замены переменной. Квадратные уравнения. Алгебра 8 класс. Примеры с решением.
Видео:Урок 1. №20 ОГЭ. Биквадратные уравнения. Как делать замену, чтобы не запутаться?Скачать

Урок 2. Биквадратные уравнения. Замена переменной в уравнениях. Алгебра 8 класс.
Биквадратные уравнения. Уравнения 4-й степени. Замена переменной в уравнениях. Решение уравнений, приводящихся к квадратным, путем замены переменной. Какое уравнение является биквадратным. Определение биквадратного уравнения. Как решать биквадратное уравнение. Как найти корни биквадратного уравнения. Алгебра 8 класс. Примеры с решением.
Урок 3. Замена переменной. Решение уравнений, приводящихся к квадратным. Алгебра 8 класс.
Решение уравнений, приводящихся к квадратным путем замены. Алгебра 8 класс. Замена переменной в уравнениях. Примеры с решением.
Урок 4. Замена переменной в уравнениях, приводящихся к квадратным.
Решение уравнений, приводящихся к квадратным путем замены. Алгебра 8 класс. Замена переменной в уравнениях. Примеры с решением.
Пример 1: Решите уравнение методом замены переменной:
Если необходимо решить уравнение вида (x+A)(x+B)(x+C)(x+D) = m где А, В, С, D и m — некоторые константы, то группируем попарно скобки таким образом, чтобы была равна сумма констант, входящих в эти скобки.
Например, если А+D = В+C, то записываем: (x+A)(x+D)(x+B)(x+C) = m
- Попарно раскрываем скобки: (x2+Ax+Dх + AD)(x2+Bx+Cх +DC) = m (x2+(A+D)х + AD)(x2+(B+C)х + DC) = m
- Делаем замену x2+(A+D)х = t Получаем уравнение (t + AD)(t + DC) = m
- После раскрытия скобок получим обычное квадратное уравнение.
Урок 5. Решение дробно-рациональных уравнений методом замены.
Решение дробно-рациональных уравнений методом замены. Алгебра 8 класс. Как сделать замену в дробно-рациональном уравнении? Решение рационального уравнения заменой. Обратные числа. Какие числа называются взаимно обратными? Взаимно-обратные дроби. Как правильно сделать замену взаимно-обратных дробей. Примеры с решением. Задания с объяснением.
Урок 6. Решение дробно-рациональных уравнений методом замены переменной. Алгебра 8 класс.
Решение дробно-рациональных уравнений методом замены. Задания с *. Алгебра 8 класс. Как сделать замену в дробно-рациональном уравнении? Как правильно возвести в квадрат при замене переменной. Как определить что заменять и какую замену делать. Решение рационального уравнения заменой. Примеры с решением. Задания с объяснением.
Урок 7. Решение уравнений методом замены. Как понизить степень уравнения заменив переменную?
Решение дробно-рациональных уравнений методом замены. Как понизить степень уравнения заменив переменную? Задания с *. Алгебра 8 класс. Как сделать замену в рациональном уравнении? Уравнения 4-й степени. Понизить степень уравнения, сделав замену. Как определить что заменять и какую замену делать. Решение рационального уравнения заменой. Примеры с решением. Задания с объяснением.
Урок 8. Замена переменной. Решение уравнений. Однородные уравнения.
Однородные уравнения второй степени. Определение однородного уравнения. Методы решения однородных уравнений. Как понять, что уравнение однородное. Решение однородных уравнений методом замены переменной. Решение уравнений методом замены переменной. Решить уравнение. Решить заменой. Примеры с решением. Задания с объяснением. Алгебра 8 класс.
Видео:Решение уравнения методом замены переменнойСкачать

Решение уравнений, сводящихся к квадратным
Биквадратные уравнения
Биквадратным уравнением называется уравнение вида:
$$ ax^4+bx^2+c = 0, a neq 0 $$
Алгоритм решения биквадратного уравнения
Шаг 1. Ввести новую переменную: $z = x^2 ge 0$.
Переписать уравнение для новой переменной: $az^2+bz+c = 0$
Шаг 2. Решить полученное квадратное уравнение.
Если $D gt 0$, $z_ = frac<-b pm sqrt> $. Проверить условие $z ≥ 0$, если положительных корней нет, решений нет, переход на шаг 4.
Если D = 0,$z_0 = -frac$. Проверить условие $z ge 0$, если корень отрицательный, решений нет, переход на шаг 4.
Если $D lt 0$, решений нет, переход на шаг 4.
Шаг 3.Если после шага 2 остались положительные корни, найти x: $x = pm sqrt$.
Шаг 4. Работа завершена.
Шаг 1. $z = x^2 ge 0, z^2+7z-30 = 0$
$z_1 = -10 lt 0, z_2 = 3 gt 0 $
Шаг 3. Находим корни из положительного $z: x_ = pm sqrt$
Метод разложения на множители
Решение уравнений, в которые переменная x входит с различными натуральными степенями и вещественными коэффициентами, по существу, является поиском корней многочлена.
Число $x_0$ называют корнем многочлена $P_n (x) = a_n x^n+a_ x^ + ⋯ + a_1 x+a_0$ если $P_n (x_0 ) = 0$.
Для многочлена $P_n$ (x) произвольной степени n справедливо следующее.
Если $x = x_0$ является корнем многочлена $P_n$ (x), то $P_n (x) = (x-x_0) P_ (x)$, где $P_ (x)$ — многочлен степени n-1.
Таким образом, разными способами находя корни и формируя скобки, можно постепенно добиваться понижения степени «оставшегося» многочлена, пока не будут найдены все корни.
При разложении многочлена
- множители вида (x-a) называют линейными множителями ;
- множители вида $ (x^2+bx+c)$, для которых $D lt 0$, называют неприводимыми квадратичными множителями .
Любой многочлен $P_n$ (x) можно представить в виде конечного числа линейных и/или неприводимых квадратичных множителей.
Причём, такое представление единственно с точностью до порядка множителей.
Для разложения многочленов на множители применяются разные методы:
- вынесение общего множителя за скобку (см. §19 справочника для 7 класса);
- группировка (см. §20 справочника для 7 класса);
- формулы сокращенного умножения (см. §25 справочника для 7 класса);
- метод неопределённых коэффициентов;
- выделение полного квадрата и т.п.
Решим уравнение $2x^3-x^2-8x+4 = 0$.
Раскладываем на множители: $x^2 (2x-1)-4(2x-1) = 0$
$$ (x^2-4)(2x-1) = 0 Rightarrow (x-2)(x+2)(2x-1) = 0 $$
Корни уравнения: $x_1 = 2, x_2 = -2, x_3 = frac$
Метод замены переменной
Замена переменной – это уравнение, с помощью которого можно упростить исходное уравнение, и перейти к решению системы из двух более простых уравнений:
$Исходное quad сложное quad уравнение iff <left< begin Новая quad переменная quad (урав. quad связи quad со quad старой quad переменной \ Исходное quad урав. quad в quad «упрощ.» quad виде end right.>$
Например, для биквадратных уравнений:
$$ ax^4+bx^2+c = 0 iff <left< begin z = x^2 ge 0 \ az^2+bz+c = 0 end right.> $$
Можно предложить аналогичные схемы для других уравнений:
$$ ax+b sqrt+c = 0 iff <left< begin z = sqrt ge 0 \ az^2+bz+c = 0 end right.> $$
И, в общем виде, для любой рациональной степени n:
$$ ax^+bx^n+c = 0 iff <left< begin z = x^n \ az^2+bz+c = 0 end right.> , n in Bbb Q $$
В других случаях замена переменной не настолько очевидна.
Но при удачном выборе, этот метод очень упрощает задачу.
Раскроем скобки:$ x^2-x = frac$. Сделаем замену:
$$ z = frac Rightarrow z(z-2) = 24 Rightarrow z^2-2z-24 = 0 Rightarrow (z-6)(z+4) = 0 Rightarrow left[ begin z_1 = -4 \ z_2 = 6 end right.$$
Возвращаемся к исходной переменной x:
$$ left[ begin x^2-x = -4 \ x^2-x = 6 end right. Rightarrow left[ begin x^2-x+4 = 0 \ x^2-x-6 = 0 end right. Rightarrow left[ begin D lt 0, x in varnothing \ (x-3)(x+2) = 0 end right. Rightarrow left[ begin x_1 = -2 \ x_2 = 3 end right. $$
При использовании метода замены переменной не забывайте возвращаться к исходной переменной.
Выделение полного квадрата
Метод выделения полного квадрата является одним из методов разложения на множители. Его идея – представить многочлен в виде разности квадратов двух других многочленов степенью пониже, и разложить разность на две скобки:
$$ P_n (x) = Q_k^2 (x)-R_m^2 (x) = (Q_k (x)-R_m (x))(Q_k (x)+R_m (x)) $$
Такое разложение не всегда возможно.
Рассмотрим выделение полного квадрата для квадратного трёхчлена:
$$ = a Biggl(x+frac Biggr)^2 — frac = a Biggl(x+ frac Biggr)^2- frac, D = b^2-4ac $$
Нами выделен полный квадрат $(x+frac)^2$.
Данное выражение используется для построения и анализа графиков парабол (см. §28 данного справочника).
А его разложение на две линейные скобки, известное как теорема Виета (см. §26 данного справочника), возможно только при условии $D ge 0$.
Решить уравнение $x^4+4x^2-1 = 0$
Выделим полный квадрат и разложим на множители:
$$ left[ begin x^2+2-sqrt = 0 \ x^2+2+sqrt = 0 end right. Rightarrow left[ begin x^2 = sqrt -2 gt 0 \ x^2 = -(2+sqrt) lt 0 end right. Rightarrow x_1,2 = pm sqrt<sqrt-2> $$
Примеры
Пример 1. Решите биквадратные уравнения:
Делаем замену: $2x^4+7x^2-4 = 0 iff <left< begin z = x^2 ge 0 \ 2z^2+7z-4 = 0 end right.>$
Решаем квадратное уравнение: $D = 7^2-4 cdot 2 cdot (-4) = 49+32 = 81 = 9^2$
$$ z = frac = left[ begin z_1 = -4 lt 0 \ z_2 = frac gt 0 end right. $$
Выбираем положительный z и возвращаемся к исходной переменной x:
Делаем замену: $(x+3)^4-10(x+3)^2+24 = 0 iff <left< begin z = (x+3)^2 ge 0 \ z^2-10z+24 = 0 end right.>$
Решаем квадратное уравнение: $z^2-10z+24 = 0 Rightarrow (z-4)(z-6) = 0 Rightarrow left[ begin z_1 = 4 \ z_2 = 6 end right.$
Берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin (x+3)^2 = 4 \ (x+3)^2 = 6 end right. Rightarrow left[ begin x+3 = pm sqrt \ x+3 = pm sqrt end right. Rightarrow left[ begin x_ = -3 pm 2 \ x_ = -3 pm sqrt end right. Rightarrow left[ begin x_1 = -5 \ x_2 = -1 \ x_ = -3 pm sqrt end right. $$
Пример 2. Решите уравнения аналогичные биквадратным:
Делаем замену: $x+4 sqrt-60 = 0 iff <left< begin z = sqrt ge 0 \ z^2+4z-60 = 0 end right.>$
Решаем квадратное уравнение: $ z^2+4z-60 = 0 Rightarrow (z+10)(z-6) = 0 Rightarrow left[ begin z_1 = -10 \ z_2 = 6 end right.$
Выбираем положительный корень и возвращаемся к исходной переменной:
Делаем замену: $(x-1)^6-7(x-1)^3-8 = 0 iff <left< begin z = (x-1)^3 \ z^2-7z-8 = 0 end right.>$
Решаем квадратное уравнение: $ z^2-7z-8 = 0 Rightarrow (z+1)(z-8) = 0 Rightarrow left[ begin z_1 = -1 \ z_2 = 8 end right.$
При замене куба знак z может быть любым, берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin (x-1)^3 = -1 \ (x-1)^3 = 8 end right. Rightarrow left[ begin x-1 = -1 \ x-1 = 2 end right. Rightarrow left[ begin x_1 = 0 \ x_2 = 3 end right. $$
Пример 3. Решите уравнения с помощью замены переменной:
Заметим, что $(x+3)^2 = x^2+6x+9$. Получаем:
$$ (x^2+6x)^2-(x^2+6x+9) = 33 Rightarrow (x^2+6x)^2-(x^2+6x)-42 = 0 $$
Решаем квадратное уравнение: $ z^2-z-42 = 0 Rightarrow (z+6)(z-7) = 0 Rightarrow left[ begin z_1 = -6 \ z_2 = 7 end right.$
Берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin x^2+6x = -6 \ x^2+6x = 7 end right. Rightarrow left[ begin x^2+6x+6 = 0 \ x^2+6x-7=0 end right. Rightarrow left[ begin D = 12, x = frac<-6 pm 2 sqrt> \ (x+7)(x-1) = 0 end right. Rightarrow left[ begin x_ = -3 pm sqrt \ x_3 = -7 \ x_4 = 1 end right. $$
Делаем замену: $ frac + frac = 2 iff left[ begin z = x^2+3 ge 3 \ frac + frac = 2 end right.$
Решаем уравнение относительно z:
$$ frac + frac = 2 Rightarrow frac = frac Rightarrow 4(z+1)+5z = 2z(z+1) $$
$$ 2z^2+2z-9z-4 = 0 Rightarrow 2z^2-7z-4 = 0 $$
$$ D = 7^2-4 cdot 2 cdot (-4) = 49+32 = 81 = 9^2 $$
$$ z = frac = left[ begin z_1 = — frac lt 3 \ z_2 = 4 gt 3 end right. $$
Выбираем корень больше 3 и возвращаемся к исходной переменной:
$$ x^2+3 = 4 Rightarrow x^2 = 1 Rightarrow x_ = pm 1$$
Пример 4*. Решите уравнения:
Приведём это уравнение к биквадратному.
В линейных множителях (x+a) выберем все a =
Найдем их среднее арифметическое (см. §52 справочника для 7 класса)
Замена переменных $z = x+a_$:
Упрощаем уравнение, используя формулу разности квадратов:
$$ (z^2-9)(z^2-1) = 945 Rightarrow z^4-10z^2+9 = 945 Rightarrow z^4-10z^2-936 = 0 $$
Получили биквадратное уравнение.
Делаем замену: $z^4-10z^2-936 = 0 iff <left< begin t = z^2 ge 0 \ t^2-10t-936 = 0 end right.> $
Решаем квадратное уравнение:
$$ D = 100+4 cdot 936 = 3844 = 62^2, t = frac = left[ begin t_1 = -26 lt 0 \ t_2 = 36 gt 0 end right. $$
Выбираем положительный корень и возвращаемся к переменной z:
$$ z = pm sqrt = pm sqrt = pm 6 $$
Возвращаемся к исходной переменной x:
$$ x = z-4 = pm 6-4 = left[ begin x_1 = -10 \ x_2 = 2 end right. $$
$$ z- frac =2,1 |times z (z neq 0) $$
$$ z^2-2,1z-1 = 0 Rightarrow D = 2,1^2+4 = 8,41 = 2,9^2; z = frac = left[ begin z_1 = -0,4 \ z_2 = 2,5 end right. $$
Берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin frac = -0,4 \ frac = 2,5 end right. Rightarrow left[ begin x^2+1 = -0,4x \x^2+1 = 2,5x end right. Rightarrow left[ begin x^2+0,4x+1 = 0 \ x^2-2,5x+1 = 0 end right. $$
В первом уравнении $D = 0,4^2-4 lt 0$, решений нет.
Во втором уравнении (x-2)(x-1/2) = 0 $Rightarrow left[ begin x_1 = frac \ x_2 = 2 end right.$
🔍 Видео
Решение биквадратных уравнений. Практическая часть. 2ч. 8 класс.Скачать

КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Биквадратные уравнения. 8 класс алгебра.Скачать

Биквадратное уравнениеСкачать

ОГЭ 2019 ЗАДАНИЕ 21. Биквадратное уравнение.Скачать

Решение биквадратных уравнений. Практическая часть. 1ч. 8 класс.Скачать

Уравнения, сводящиеся к квадратным. Биквадратное уравнениеСкачать

9. Биквадратное уравнение. Замена переменной.Скачать

БИКВАДРАТНОЕ УРАВНЕНИЕ класс математикаСкачать

Замена в уравнениях. Тип №1 (Биквадратное уравнение)Скачать

Биквадратное уравнениеСкачать
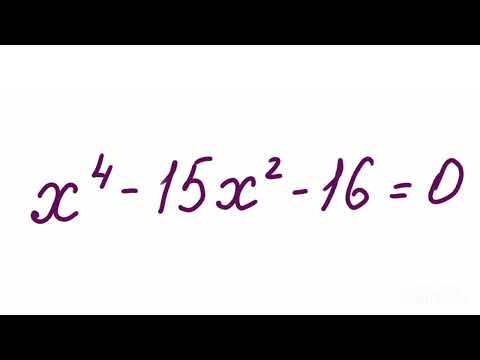
Решение уравнений сводящихся к квадратным уравнениям. Биквадратные уравнения – 8 класс алгебраСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Как решают уравнения в России и СШАСкачать

Биквадратное уравнениеСкачать
