план-конспект урока по математике (4 класс) на тему
Конспект урока по математике в 4 классе «Уравнения с неизвестными в обеих частях» система Л.В.Занкова
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- Решение уравнений с двумя неизвестными
- Определение
- Решение задач
- Система уравнений с двумя неизвестными
- Метод подстановки
- Метод сложения
- Графический метод
- Видео
- Уравнения с двумя переменными (неопределенные уравнения)
- Урок 1.
- Ход урока.
- 1) Орг. момент.
- 2) Актуализация опорных знаний. Определение. Линейным уравнением с двумя переменными называется уравнение вида mx + ny = k, где m, n, k – числа, x, y – переменные. Определение. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство. Уравнения с двумя переменными, имеющими одни и те же решения, называются равносильными. 1. 5x+2y=12 (2)y = -2.5x+6 Данное уравнение может иметь сколько угодно решений. Для этого достаточно взять любое значение x и найти соответствующее ему значение y. Пусть x = 2, y = -2.5•2+6 = 1 x = 4, y = -2.5•4+6 =- 4 Пары чисел (2;1); (4;-4) – решения уравнения (1). Данное уравнение имеет бесконечно много решений. 3) Историческая справка Неопределенные (диофантовы) уравнения – это уравнения, содержащие более одной переменной. В III в. н.э. – Диофант Александрийский написал “Арифметику”, в которой расширил множество чисел до рациональных, ввел алгебраическую символику. Так же Диофант рассмотрел проблемы решения неопределенных уравнений и им даны методы решения неопределенных уравнений второй и третьей степени. 4) Изучение нового материала. Определение: Неоднородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = k, где m, n, k, x, y Z k0 Если свободный член k в уравнении (1) не делится на наибольший общий делитель (НОД) чисел m и n, то уравнение (1) не имеет целых решений. Пример: 34x – 17y = 3. НОД (34; 17) = 17, 3 не делится нацело на 17, в целых числах решения нет. Пусть k делится на НОД (m, n). Делением всех коэффициентов можно добиться, что m и n станут взаимно простыми. Если m и n уравнения (1) взаимно простые числа, то это уравнение имеет по крайней мере одно решение. Если коэффициенты m и n уравнения (1) являются взаимно простыми числами, то это уравнение имеет бесконечно много решений: где (; ) – какое-либо решение уравнения (1), t Z Определение. Однородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = 0, где (2) m, n, x, y Z Если m и n – взаимно простые числа, то всякое решение уравнения (2) имеет вид 5) Домашнее задание. Решить уравнение в целых числах: 9x – 18y = 5 x + y= xy Несколько детей собирали яблоки. Каждый мальчик собрал по 21 кг, а девочка по 15 кг. Всего они собрали 174 кг. Сколько мальчиков и сколько девочек собирали яблоки?
- Видео
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Скачать:
| Вложение | Размер |
|---|---|
| uravneniya_s_neizvestnymi_v_obeikh_chastyakh_4_klass.doc | 51.5 КБ |
Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Предварительный просмотр:
МУНИЦИПАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СРЕДНЯЯ ШКОЛА №1 им. М.В.Ломоносова».
Тема: « Уравнения с неизвестным в обеих частях».
учитель начальных классов
Ярошенко Наталья Викторовна
Цели: 1). Продолжить работу по формированию понятия об уравнении;
2). Развивать умение решать уравнения, требующие тождественных преобразований на основе взаимосвязи между компонентами действий и на основе использования основных свойств равенств;
3). Развивать умение анализировать задачи и записывать решение алгебраическим способом;
4). Формировать вычислительные навыки.
I). Настрой на урок.
— Как прошла перемена? Садитесь.
— Сегодня на уроке решаем задачу, уравнения, изучаем новый материал;
И, конечно же. я для вас подготовила занимательно-познавательное задание.
— С какого задания хотите начать урок?
II). Устное занимательно-познавательное задание
3600: 60 П 63000: 7000 Р 72:12 Е
12х- х Л 5а + 8а К 3в + 18в Е
— Что можете сказать об этих выражениях?
( можно разделить на 2 группы – числовые, буквенные;
выражения с действиями 1, 2 ступеней;
1 группа – можно найти значения, 2 группа – нельзя, можно упростить;
Нужно использовать рациональные способы деления.)
— Устно найдите значения выражений 1 строки, а 2 строки упростите. Полученные результаты соотнесите с буквой.
— Поработайте в паре. Сравните свои записи. Какое слово у вас получилось?
— ИОГАНН КЕПЛЕР – немецкий учёный-астроном, сделавший свои открытия в начале XVII века.
Путём точных математических расчётов установил законы движения планет (их 3). О достижениях этого учёного вы подробно узнаете в старших классах на уроках астрономии.
А вас знания законов математики и точные математические расчёты приведут к открытиям на сегодняшнем уроке.
— Выполняя следующее задание, попробуйте определить тему урока.
III). Изучение нового.
5х + 15=80 5х + 15 = 80 – 8х
— Сравните данные уравнения. Что о них можете сказать? ( для решения первого уравнения нужно выполнить 2 действия, для второго больше;
Первое уравнения можем решить. 2 – не умеем решать.
— Самостоятельно решите то уравнение, которое умеете решать. ( два ученика работают на доске.)
— Чем второе уравнение отличается от тех, которые уже решали? (неизвестное число в обеих частях)
— Кто уже может определить тему сегодняшнего урока? (Уравнения с неизвестным в обеих частях).
— Вы правильно определили тему урока.
( Учитель открывает тему на доске).
Уравнения с неизвестным в обеих частях
— Сегодня мы будем учиться решать уравнения с неизвестным в обеих частях.
— Попробуйте предположить: корни данных уравнений будут одинаковые или разные?
— Запишите новое уравнение в тетрадь.
— Для упрощения нового уравнения вам потребуются старые знания.
— Обсудите в парах, какие знания вам потребуются. (1 свойство равенства).
Учитель на доске под комментирование учеников:
— Выполним проверку. Что надо помнить? (найденное число подставляем в первое уравнение).
— Подведём итог нашей работе.
— Продолжите фразу: «Теперь я знаю как…»
«Теперь я смогу попробовать самостоятельно …»
— А попробуете вы свои силы в решении новых уравнений после физминутки.
Физминутка «Дотянись до звезды»
— Встаньте поудобнее и закройте глаза. Сделайте 3 глубоких вдоха и выдоха.
— Представьте. что над вами ночное небо. усыпанное звёздами.
— Выберете звёздочку (это ваша мечта).
— Откройте глаза и протяните руки к небу, чтобы дотянуться до своей звезды.
— Снимите её с неба и бережно положите перед собой.
— Я уверена, что мечта у вас не единственная. Сорвите сами ещё несколько звёздочек. Дышите так:
Тянешься за звездой – глубокий вдох.
Выдох- кладёте звезду к первой.
IV). Самостоятельная работа.
— Откройте с.30 № 294 (6 задание).
— Попробуйте самостоятельно решить. Когда закончите работу, проверьте её друг у друга.
— Постарайтесь рассказать, как вы решали уравнение.
— Молодцы, вы замечательно справились с работой, помогая друг другу.
V). Решение задачи. (Задача – на карточке).
Скорость движения Земли на 6 км/ч больше скорости Марса. С какой скоростью движется каждая планета?
— Прочитайте задачу про себя.
— Что заметили? ( не хватает данных )
— Добавьте в условие недостающие данные, чтобы задачу можно было решить.
— Прочитайте получившуюся задачу.
— Запишем её кратко.
— Что обозначает число 54?
— Перефразируйте вопрос задачи.
— Обсудите решение задачи в парах. ( удобнее решить уравнением)
— Какое искомое удобно взять за х?
— Так как общая скорость двух планет равна 54км/ч, получаю уравнение:
х=24 (км/ч) – скорость Марса
24+6=30 (км/ч) – скорость Земли.
-Проверьте правильность решения задачи.
— Найдите другой способ проверки правильности решения задачи. (другой способ решения).
— Попробуйте решить эту задачу по действиям.
— Посмотрите, поможет ли вам такая схема краткой записи:
(54-6):2=24 (км/ч) – скорость Марса
24+6=30 (км/ч) – скорость Земли
— Подведите итог.( задача решена верно)
VI) Новые знания.
— Вы сейчас решили задачу уравнением и по действиям.
У этих способов решения задачи в математике есть свои названия.
— Если для решения задачи используют уравнение –
Алгебра – часть науки математики.
— это когда задачу решают… ( по действиям или сложным выражением).
— Арифметика – это тоже часть математики. Многое из того. Что мы изучали в предыдущих классах, тоже относится к арифметике.
— К самым древним задачам на составление уравнений относятся задачи из древнеегипетских папирусов. Сохранились 2 математических папируса. Одна из этих задач в № 347. По желанию попробуйте её решить дома.
VII). Самостоятельная работа (разноуровневая)
VIII) Подведение итогов.
— Что можете сказать о сегодняшнем уроке? ( Я узнал… Я научился…).
— Продолжите фразу: «Мне ещё сложно…»
— Не переживай, над этой темой мы ещё будем работать.
— Ребята, спасибо вам за работу! Я с удовольствием ставлю «5»-….
— Без помощи и поддержки друг друга мы не смогли бы добиться цели.
Видео:УРАВНЕНИЕ 4 КЛАСС МАТЕМАТИКА УЧИМСЯ РЕШАТЬ УРАВНЕНИЯ МЕТОДИКА ОБУЧЕНИЯ РЕШАЕМ УРАВНЕНИЯ #уравнениеСкачать

По теме: методические разработки, презентации и конспекты
Классный час «3 декабря-День Неизвестного солдата» ( 3-4 класс)
Во всем мире памятники погибшим на войне устанавливают для того, чтобы люди помнили, за что воины отдали свою жизнь. Могилы солдат часто бывают безымянными, и раньше к ним не приходили почтить их памя.
Конспект урока на тему: «Задачи на нахождение неизвестного третьего слагаемого» 2 класс
Конспект урока на тему: «Задачи на нахождение неизвестного третьего слагаемого» 2 класс (конспект + презентация).
Конспект урока на тему: «Задачи на нахождение неизвестного третьего слагаемого» 2 класс
Конспект урока на тему: «Задачи на нахождение неизвестного третьего слагаемого» 2 класс.
Конспект урока математики «Задачи на нахождение неизвестного третьего слагаемого» (2 класс)
Цели деятельности учителя:формирование умения решать задачи на нахождение неизвестного третьего слагаемого;совершенствование вычислительного навыка и навыка устного счета;развитие внимания и логическо.
Технологическая карта урока математики «Задачи на нахождение неизвестного третьего слагаемого» 2 класса УМК «Школа России»
Цели деятельности учителя: научить решать задачи на нахождение третьего слагаемого, познакомить с алгоритмом решения задач на нахождение третьего слагаемого.Планируемые результатыПредметные: Зна.
Технологическая карта по математике на тему: «Задачи на нахождение неизвестного третьего слагаемого» 2 класс
Конспект урока (математика)Тема: «Задачи на нахождение неизвестного третьего слагаемого» Цели деятельности учителя: формирование умения решать задачи на нахождение неизвестного .
Технологическая карта урока по математике на тему «Задачи на нахождение неизвестного третьего слагаемого» 2 класс
Тема: «Задачи на нахождение неизвестного третьего слагаемого»Цели деятельности учителя: Продолжить работу над задачами на нахождение неизвестного третьего слагаемого.Планируемые результаты.
Видео:4 класс: как легко составить уравнение по задаче?Скачать

Решение уравнений с двумя неизвестными
В математике большая часть задач ориентирована на решение стандартных уравнений, в которых представлена одна переменная. Однако, некоторые из них, помимо числовых выражений, содержат одновременно две неизвестные. Перед тем как приступить к решению такого уравнения, стоит изучить его определение.
Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Определение
Итак, уравнением с двумя неизвестными называют любое равенство следующего типа:
a*x + b*y =с, где a, b, c — числа, x, y — неизвестные переменные.
Ниже приведены несколько примеров:
Уравнение с двумя неизвестными точно так же, как и с одной, имеет решение. Однако такие выражения, как правило, имеют бесконечное множество разных решений, поэтому в алгебре их принято называть неопределенными.
Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Решение задач
Чтобы решить подобные задачи, необходимо отыскать любую пару значений x и y, которая удовлетворяла бы его, другими словами, обращала бы уравнение с неизвестными x и y в правильное числовое равенство. Найти удовлетворяющую пару чисел можно при помощи метода подбора.
Для наглядности объяснений подберем корни для выражения: y-x = 6.
При y=5 и x=-1 равенство становится верным тождеством 5- (-1) = 6. Поэтому пару чисел (-1; 5) можно считать корнями выражения y-x = 6. Ответ: (-1; 5).
Необходимо отметить, что записывать полученный ответ по правилам необходимо в скобках через точку с запятой. Первым указывается значение х, вторым — значение y.
У равенств такого вида может и не быть корней. Рассмотрим такой случай на следующем примере: x+y = x+y+9
Приведем исходное равенство к следующему виду:
В результате мы видим ошибочное равенство, следовательно, это выражение не имеет корней.
При решении уравнений можно пользоваться его свойствами. Первое их них: каждое слагаемое можно вынести в другую часть выражения. Вместе с этим обязательно нужно поменять знак на обратный. Получившееся равенство будет равнозначно исходному.
Например, из выражения 20y — 3x = 16 перенесем неизвестное y в другую его часть.
Оба равенства равносильны.
Второе свойство: допустимо умножать или делить части выражения на одинаковое число, не равное нолю. В итоге получившиеся равенства будут равнозначны.
Оба уравнения также равносильны.
Видео:ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

Система уравнений с двумя неизвестными
Система уравнений представляет собой некоторое количество равенств, выполняющихся одновременно. В большинстве задач приходится находить решение системы, состоящей из двух равенств с двумя переменными.
Для решения системы уравнений необходимо найти пару чисел, обращающих оба уравнения системы в правильное равенство. Решением может служить одна пара чисел, несколько пар чисел или вовсе их отсутствие.
Решить подобные системы уравнений можно, применяя следующие методы.
Метод подстановки
- Выражаем неизвестное из любого равенства через вторую переменную.
- Подставляем получившееся выражение неизвестного во второе равенство и решаем его.
- Делаем подстановку полученного значения неизвестного и вычисляем значение второго неизвестного.
Метод сложения
- Приводим к равенству модули чисел при каком-либо неизвестном.
- Производим вычисление одной из переменных, произведя сложение или вычитание полученных выражений.
- Подставляем найденное значение в какое-либо уравнение в первоначальной системе и вычисляем вторую переменную.
Графический метод
- Выражаем в каждом равенстве одну переменную через другую.
- Строим графики двух имеющихся уравнений в одной координатной плоскости.
- Определяем точку их пересечения и ее координаты. На этом шаге у вас может получиться три варианта: графики пересекаются — у системы единственно верный вариант решения; прямые параллельны друг другу — система решений не имеет; графики совпадают — у системы бесконечно много решений.
- Делаем проверку, подставив полученные значения в исходную систему равенств.
При нахождении корней у одной системы всеми этими способами у вас обязательно должен получиться одинаковый результат, если вы, конечно, все сделали правильно.
В настоящее время есть возможность решения подобных задач с помощью встроенных средств офисной программы Excel, а также на специализированных онлайн-ресурсах и калькуляторах. С помощью них вы легко можете проверить правильность своих вычислений и результатов.
Надеемся, что наша статья помогла вам в освоении этой базовой темы школьной математики. Если же вы пока не можете справиться с решением уравнений такого вида, не расстраивайтесь. Для понимания и закрепления изученной темы рекомендуется как можно больше практиковаться, и тогда у вас без труда получится решать задачи любой сложности. Желаем вам удачи в покорении математических вершин!
Видео:Линейное уравнение с двумя переменными.Скачать
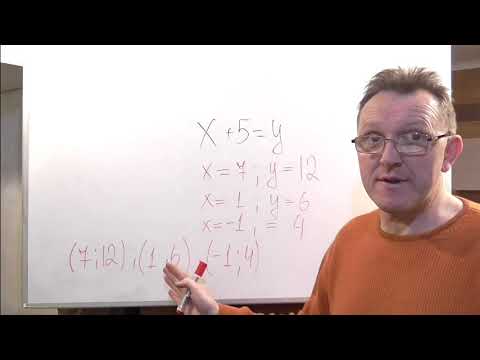
Видео
Из этого видео вы узнаете, как решать уравнения с двумя неизвестными.
Видео:Математика 4 класс.Решение сложных уравнений. Пример 3.Скачать

Уравнения с двумя переменными (неопределенные уравнения)
Разделы: Математика
Обращение автора к данной теме не является случайным. Уравнения с двумя переменными впервые встречаются в курсе 7-го класса. Одно уравнение с двумя переменными имеет бесконечное множество решений. Это наглядно демонстрирует график линейной функции, заданный в виде ax + by=c. В школьном курсе учащиеся изучают системы двух уравнений с двумя переменными. В результате из поля зрения учителя и, поэтому ученика, выпадает целый ряд задач, с ограниченными условиями на коэффициент уравнения, а также методы их решения.
Речь идет о решении уравнения с двумя неизвестными в целых или натуральных числах.
В школе натуральные и целые числа изучаются в 4-6-х классах. К моменту окончания школы не все ученики помнят различия между множествами этих чисел.
Однако задача типа “решить уравнение вида ax + by=c в целых числах” все чаще встречается на вступительных экзаменах в ВУЗы и в материалах ЕГЭ.
Решение неопределенных уравнений развивает логическое мышление, сообразительность, внимание анализировать.
Я предлагаю разработку нескольких уроков по данной теме. У меня нет однозначных рекомендаций по срокам проведения этих уроков. Отдельные элементы можно использовать и в 7-м классе (для сильного класса). Данные уроки можно взять за основу и разработать небольшой элективный курс по предпрофильной подготовке в 9-м классе. И, конечно, этот материал можно использовать в 10-11 классах для подготовки к экзаменам.
Цель урока:
- повторение и обобщение знаний по теме “Уравнения первого и второго порядка”
- воспитание познавательного интереса к учебному предмету
- формирование умений анализировать, проводить обобщения, переносить знания в новую ситуацию
Урок 1.
Ход урока.
1) Орг. момент.
2) Актуализация опорных знаний.
Определение. Линейным уравнением с двумя переменными называется уравнение вида
mx + ny = k, где m, n, k – числа, x, y – переменные.
Определение. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Уравнения с двумя переменными, имеющими одни и те же решения, называются равносильными.
1. 5x+2y=12 
Данное уравнение может иметь сколько угодно решений. Для этого достаточно взять любое значение x и найти соответствующее ему значение y.
Пусть x = 2, y = -2.5•2+6 = 1
x = 4, y = -2.5•4+6 =- 4
Пары чисел (2;1); (4;-4) – решения уравнения (1).
Данное уравнение имеет бесконечно много решений.
3) Историческая справка
Неопределенные (диофантовы) уравнения – это уравнения, содержащие более одной переменной.
В III в. н.э. – Диофант Александрийский написал “Арифметику”, в которой расширил множество чисел до рациональных, ввел алгебраическую символику.
Так же Диофант рассмотрел проблемы решения неопределенных уравнений и им даны методы решения неопределенных уравнений второй и третьей степени.
4) Изучение нового материала.
Определение: Неоднородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = k, где m, n, k, x, y 

Если свободный член k в уравнении (1) не делится на наибольший общий делитель (НОД) чисел m и n, то уравнение (1) не имеет целых решений.
Пример: 34x – 17y = 3.
НОД (34; 17) = 17, 3 не делится нацело на 17, в целых числах решения нет.
Пусть k делится на НОД (m, n). Делением всех коэффициентов можно добиться, что m и n станут взаимно простыми.
Если m и n уравнения (1) взаимно простые числа, то это уравнение имеет по крайней мере одно решение.
Если коэффициенты m и n уравнения (1) являются взаимно простыми числами, то это уравнение имеет бесконечно много решений:




Определение. Однородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = 0, где (2)
m, n, x, y 
Если m и n – взаимно простые числа, то всякое решение уравнения (2) имеет вид
5) Домашнее задание. Решить уравнение в целых числах:
Замечание. На данном уроке не представлены примеры решения уравнений в целых числах. Поэтому домашнее задание дети решают исходя из утверждения 1 и подбором.
Урок 2.
1) Организационный момент
2) Проверка домашнего задания
5 не делится нацело на 9, в целых числах решений нет.
Методом подбора можно найти решение
3) Составим уравнение:
Пусть мальчиков x, x 

Многие учащиеся, составив уравнение, не смогут его решить.
Ответ: мальчиков 4, девочек 6.
3) Изучение нового материала
Столкнувшись с трудностями при выполнении домашнего задания, учащиеся убедились в необходимости изучения их методов решений неопределенных уравнений. Рассмотрим некоторые из них.
I. Метод рассмотрения остатков от деления.
Пример. Решить уравнение в целых числах 3x – 4y = 1.
Левая часть уравнения делится на 3, следовательно, должна делиться и правая часть. Рассмотрим три случая.
- Если y = 3m, m
Z, то 4y + 1= 4•3m + 1 = 12m + 1 не делится на 3.
- Если y = 3 m + 1, то 4y +1 = 4• (3m + 1)+1 = 12m + 5 не делится на 3.
- Если y = 3 m + 2, то 4y +1 = 4• (3m + 2)+1 = 12m + 9 делится на 3, поэтому 3x = 12m + 9, следовательно, x = 4m + 3, а y = 3m + 2.
Ответ: 

Описанный метод удобно применять в случае, если числа m и n не малы, но зато разлагаются на простые сомножители.
Пример: Решить уравнения в целых числах.
Пусть y = 4n, тогда 16 — 7y = 16 – 7•4n = 16 – 28n = 4*(4-7n) делится на 4.
y = 4n+1, тогда 16 – 7y = 16 – 7• (4n + 1) = 16 – 28n – 7 = 9 – 28n не делится на 4.
y = 4n+2, тогда 16 – 7y = 16 – 7• (4n + 2) = 16 – 28n – 14 = 2 – 28n не делится на 4.
y = 4n+3, тогда 16 – 7y = 16 – 7• (4n + 3) = 16 – 28n – 21 = -5 – 28n не делится на 4.
Следовательно, y = 4n, тогда
4x = 16 – 7•4n = 16 – 28n, x = 4 – 7n
Ответ: 

II. Неопределенные уравнения 2-ой степени
Сегодня на уроке мы лишь коснемся решения диофантовых уравнений второго порядка.
И из всех типов уравнений рассмотрим случай, когда можно применить формулу разности квадратов или другой способ разложения на множители.
Пример: Решить уравнение в целых числах.
13 – простое число, поэтому оно может быть разложено на множители лишь четырьмя способами: 13 = 13•1 = 1•13 = (-1)(-13) = (-13)(-1)
Рассмотрим эти случаи
а) 
б) 
в) 
г) 
4) Домашнее задание.
Примеры. Решить уравнение в целых числах:
а)
 |  |  |
| 2x = 4 | 2x = 5 | 2x = 5 |
| x = 2 | x = 5/2 | x = 5/2 |
| y = 0 | не подходит | не подходит |
 |  |  |
| 2x = -4 | не подходит | не подходит |
| x = -2 | ||
| y = 0 |
б)
в)
Итоги. Что значит решить уравнение в целых числах?
Какие методы решения неопределенных уравнений вы знаете?
Упражнения для тренировки.
1) Решите в целых числах.
| а) 8x + 12y = 32 | x = 1 + 3n, y = 2 — 2n, n  Z Z |
| б) 7x + 5y = 29 | x = 2 + 5n, y = 3 – 7n, n  Z Z |
| в) 4x + 7y = 75 | x = 3 + 7n, y = 9 – 4n, n  Z Z |
| г) 9x – 2y = 1 | x = 1 – 2m, y = 4 + 9m, m  Z Z |
| д) 9x – 11y = 36 | x = 4 + 11n, y = 9n, n  Z Z |
| е) 7x – 4y = 29 | x = 3 + 4n, y = -2 + 7n, n  Z Z |
| ж) 19x – 5y = 119 | x = 1 + 5p, y = -20 + 19p, p  Z Z |
| з) 28x – 40y = 60 | x = 45 + 10t, y = 30 + 7t, t  Z Z |
2) Найти целые неотрицательные решения уравнения:
| а) 8x + 65y = 81 | x = 2, y = 1 |
| б) 17x + 23y = 183 | x = 4, y = 5 |
3) Найти все пары целых чисел (x; y), удовлетворяющие следующим условиям
| а) x + y = xy | (0;0), (2;2) |
б)  | (1;2), (5;2), (-1;-1), (-5;-2) |
Число 3 можно разложить на множители:
a)  | б)  | в)  | г)  |
в)  | (11;12), (-11;-12), (-11;12), (11;-12) |
г)  | (24;23), (24;-23), (-24;-23), (-24;23) |
д)  | (48;0), (24;1), (24;-1) |
е)  | x = 3m; y = 2m, m Z Z |
| ж) y = 2x – 1 | x = m: y = 2m – 1, m  Z Z |
з)  | x = 2m; y = m; x = 2m; y = -m, m  Z Z |
и) | решений нет |
4) Решить уравнения в целых числах
 | (-3;-2), (-1;1), (0;4), (2;-2), (3;1), (5;4) |
| (x — 3)(xy + 5) = 5 | (-2;3), (2;-5), (4;0) |
| (y + 1)(xy – 1)=3 | (0;-4), (1;-2), (1;2) |
 | (-4;-1), (-2;1), (2;-1), (4;1) |
 | (-11;-12), (-11;12), (11;-12), (11;12) |
 | (-24;23), (-24;23), (24;-23), (24;23) |
5) Решить уравнения в целых числах.
а)  | (-1;0) |
б) | (5;0) |
в)  | (2;-1) |
г)  | (2; -1) |
📹 Видео
Как решают уравнения в России и СШАСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Уравнение с двумя неизвестными. Решить в целых числах. ЗадачаСкачать

Как решить уравнение #россия #сша #америка #уравненияСкачать

Решение систем уравнений методом подстановкиСкачать

Математика 4 класс (Урок№21 - Решение уравнений.)Скачать

Решение задач с помощью уравнений.Скачать

РЕШАЕМ УРАВНЕНИЕ х + 216 = 345 + 89. Примеры | МАТЕМАТИКА 4 классСкачать

Решение сложных уравнений 4-5 класс.Скачать

РЕШАЕМ УРАВНЕНИЕ х – 173 = 600 – 270. Примеры | МАТЕМАТИКА 4 классСкачать

Математика 2 класс (Урок№26 - Уравнение. Решение уравнений подбором неизвестного числа.)Скачать
















