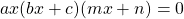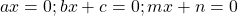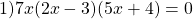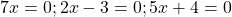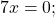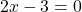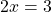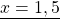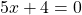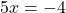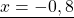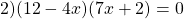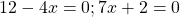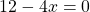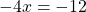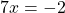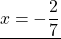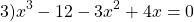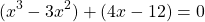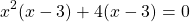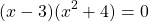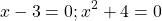Как решать уравнения правая часть которых равна нулю (2 видео)

Уравнения равные нулю

Что такое «уравнения равные нулю»?

Если в левой части уравнения стоит сумма или разность одночленов или многочленов, а в правой части — нуль, то это может быть обычное линейное уравнение.

Если левая часть уравнения представляет собой произведения двух или нескольких множителей, а правая часть — нуль, то это — уравнение типа «произведение равно нулю».

В общем виде простейшие равные нулю уравнения можно записать как

(множителей может быть больше).

Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому приравниваем к нулю каждый множитель:

и решаем каждое из полученных уравнений отдельно.

Это — уравнение типа «произведение равно нулю».

Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:

Если в уравнении, равном 0, левую часть можно разложить на множители, то такое уравнение также можно решить как уравнение типа «произведение равно 0».

Сгруппируем первое слагаемое с третьим, а четвёртое — со вторым:

Из первых скобок вынесем за скобки общий множитель x², из вторых — 4:

Общий множитель (x-3) вынесем за скобки:

Получили уравнение типа «произведение равно 0». Приравниваем к нулю каждый из множителей:

Корень первого уравнения —

Второе уравнение не имеет корней (сумма положительных чисел не может равняться нулю).

В алгебре многие уравнения сводятся к уравнениям типа «произведение равно нулю» с помощью разложения на множители.

Множители могут линейными, квадратными, логарифмическими, тригонометрическими и т.д. уравнениями.

Еще один важный частный случай уравнений, равных нулю, рассмотрим позже.

Содержание

13 комментариев
Рациональные уравнения с примерами решения
Рациональные уравнения. Равносильные уравнения
Применение условия равенства дроби нулю
Пример №202
Использование основного свойства пропорции
Пример №203
Метод умножения обеих частей уравнения на общий знаменатель дробей
Пример №204
Пример №205
Степень с целым показателем
Неполные квадратные уравнения
Основные понятия
Решение неполных квадратных уравнений
Как решить уравнение ax² = 0
Как решить уравнение ax² + с = 0
Как решить уравнение ax² + bx = 0
🎦 Видео

13 комментариев

Показательное уравнение:
3^((x+2)/(3x-4))-2*3^((5x-10)/(3x-4))-7=0
Корень известен: x=2.
Подскажите, пожалуйста, как найти решение. Преобразовать в квадратное уравнение что-то не получается.

Видео:Как решать уравнения с дробью? #shortsСкачать

Рациональные уравнения с примерами решения

Содержание:

Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Рациональные уравнения. Равносильные уравнения

два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.

Так, например, равносильными будут уравнения

Уравнения — не равносильны, так как корнем первого уравнения является число 10, а корнем второго — число 9.

Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.

1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;

2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;

3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.

Левая и правая части каждого из них являются рациональными выражениями.

Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.

В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения — дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.

Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.

Применение условия равенства дроби нулю

Напомним, что когда

Пример №202

Решите уравнение

Решение:

С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду где и — целые рациональные выражения. Имеем:

Окончательно получим уравнение:

Чтобы дробь равнялась нулю, нужно, чтобы числитель равнялся нулю, а знаменатель не равнялся нулю.

Тогда откуда При знаменатель Следовательно, — единственный корень уравнения.

Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:

Значит, решая дробное рациональное уравнение, можно:

1) с помощью тождественных преобразований привести уравнение к виду

2) приравнять числитель к нулю и решить полученное целое уравнение;

3) исключить из его корней те, при которых знаменатель равен нулю, и записать ответ.

Использование основного свойства пропорции

Если то где

Пример №203

Решите уравнение

Решение:

Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то Имеем: то есть ОДЗ переменной содержит все числа, кроме 1 и 2.

Сложив выражения в правой части уравнения, приведем его к виду: получив пропорцию:

По основному свойству пропорции имеем:

Решим это уравнение:

откуда

Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.

Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:

Таким образом, для решения дробного рационального уравнения можно:

1) найти область допустимых значений (ОДЗ) переменной в уравнении;

2) привести уравнение к виду

3) записать целое уравнение и решить его;

4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.

Метод умножения обеих частей уравнения на общий знаменатель дробей

Пример №204

Решите уравнение

Решение:

Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:

Областью допустимых значений переменной будут те значения при которых то есть все значения кроме чисел А простейшим общим знаменателем будет выражение

Умножим обе части уравнения на это выражение:

Получим: а после упрощения: то есть откуда или

Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.

Следовательно, число 12 — единственный корень уравнения. Ответ. 12.

Решая дробное рациональное уравнение, можно:

3) умножить обе части уравнения на этот общий знаменатель;

4) решить полученное целое уравнение;

5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.

Пример №205

Являются ли равносильными уравнения

Решение:

Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.

Первое уравнение имеет единственный корень а второе — два корня (решите уравнения самостоятельно). Следовательно, уравнения не являются равносильными.

Степень с целым показателем

Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:

где — натуральное число,

В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: кг. Как понимать смысл записи

Рассмотрим степени числа 3 с показателями — это соответственно

В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:

Число должно быть втрое меньше числа равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно, Равенство справедливо для любого основания при условии, что

Нулевая степень отличного от нуля числа а равна единице, то есть при

Вернемся к строке со степенями числа 3, где слева от числа записано число Это число втрое меньше, чем 1, то есть равно Следовательно, Рассуждая аналогично получаем: и т. д.

Приходим к следующему определению степени с целым отрицательным показателем:

если натуральное число, то

Видео:Уравнение в котором произведение множителей равно нулю. Алгебра 7 класс.Скачать

Неполные квадратные уравнения

О чем эта статья:

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Основные понятия

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

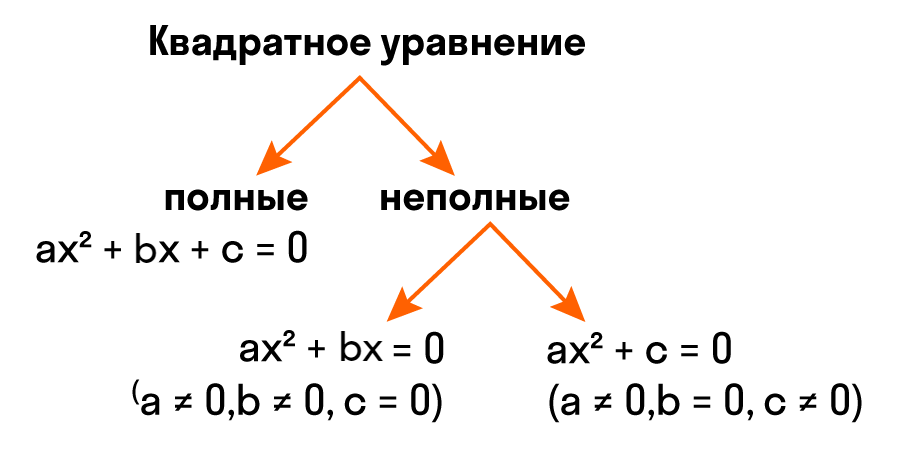
Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

если D 0, есть два различных корня.

Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.

Неполные квадратные уравнения бывают трех видов:

Если b = 0, то квадратное уравнение принимает вид ax² + 0x+c=0 и оно равносильно ax² + c = 0.
Если c = 0, то квадратное уравнение выглядит так ax² + bx + 0 = 0, иначе его можно написать как ax² + bx = 0.
Если b = 0 и c = 0, то квадратное уравнение выглядит так ax² = 0.

Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Видео:Уравнения, одна часть которого алгебраическая дробь, а другая - ноль.Скачать

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
ax² + c = 0, при b = 0;
ax² + bx = 0, при c = 0.

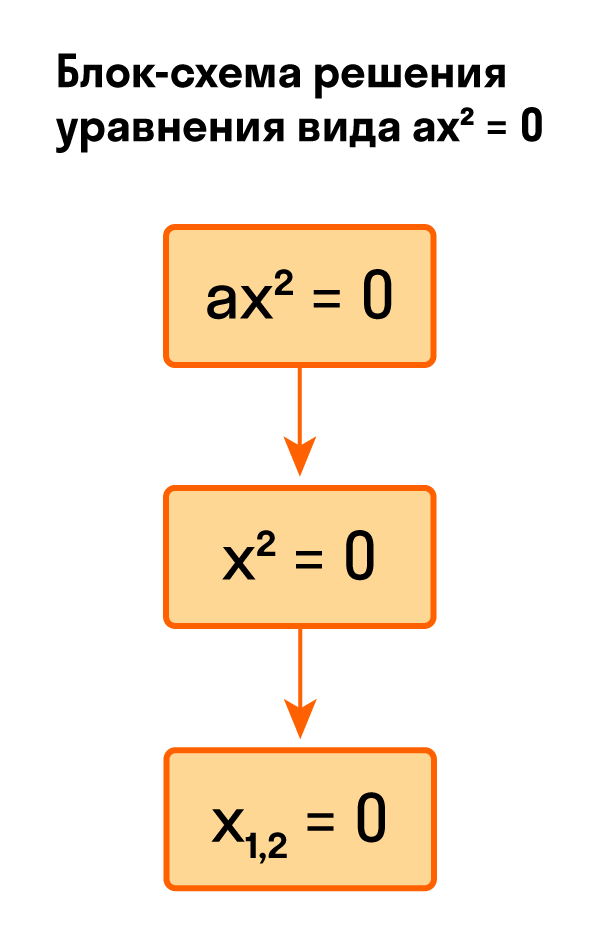
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Как решить уравнение ax² = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.

Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.

Пример 1. Решить −5x² = 0.

Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
По шагам решение выглядит так:

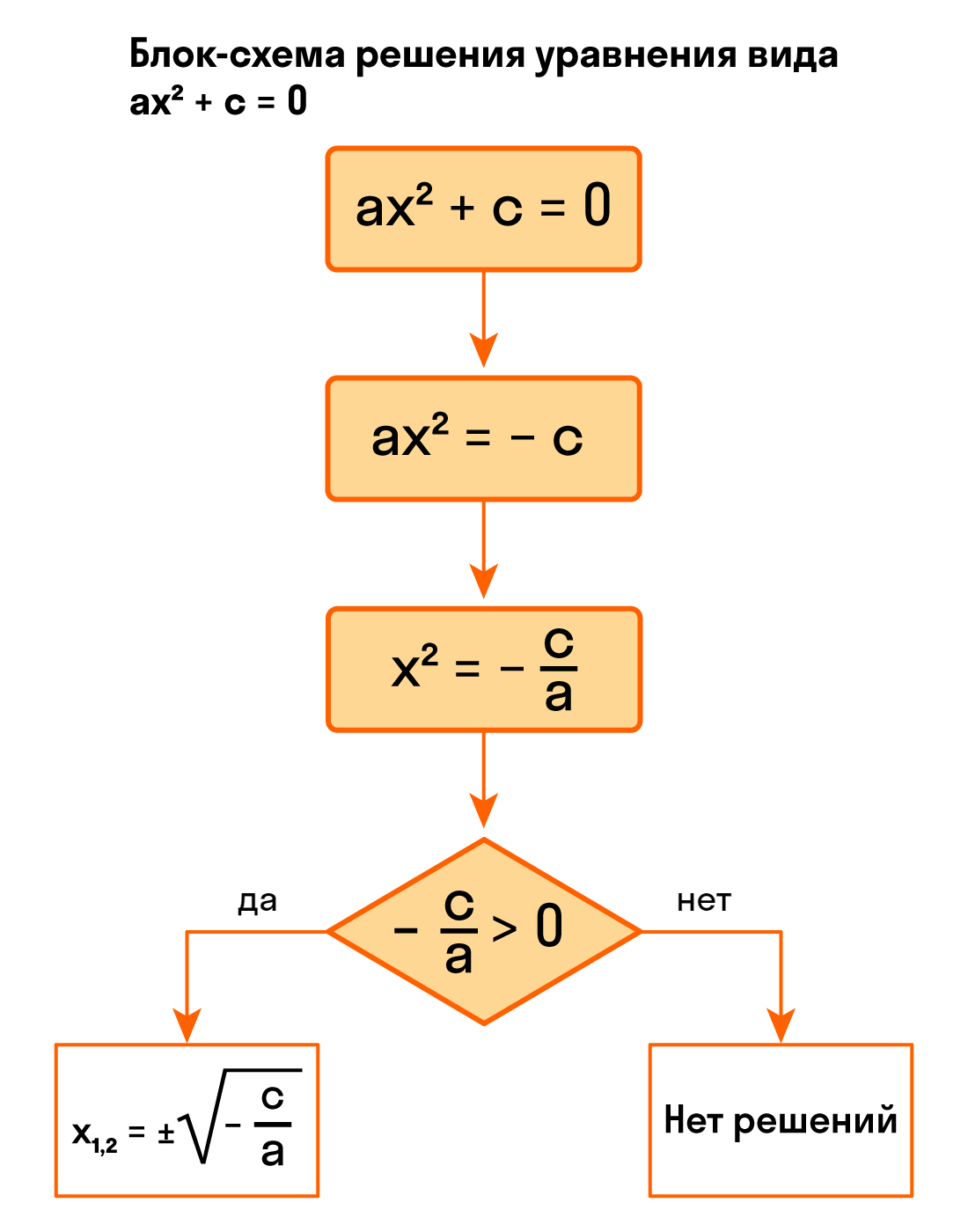
Записывайся на дополнительные уроки по математике онлайн, с нашими лучшими преподавателями! Для учеников с 1 по 11 класса!

Видео:Уравнение алгебраическая дробь равная нулю. Алгебра 8 класс.Скачать

Как решить уравнение ax² + с = 0

Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:

перенесем c в правую часть: ax² = — c,
разделим обе части на a: x² = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней.

В двух словах квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:

не имеет корней при — c/а 0.

Пример 1. Найти решение уравнения 9x² + 4 = 0.

Разделим обе части на 9:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 9x² + 4 = 0 не имеет корней.

Пример 2. Решить -x² + 9 = 0.

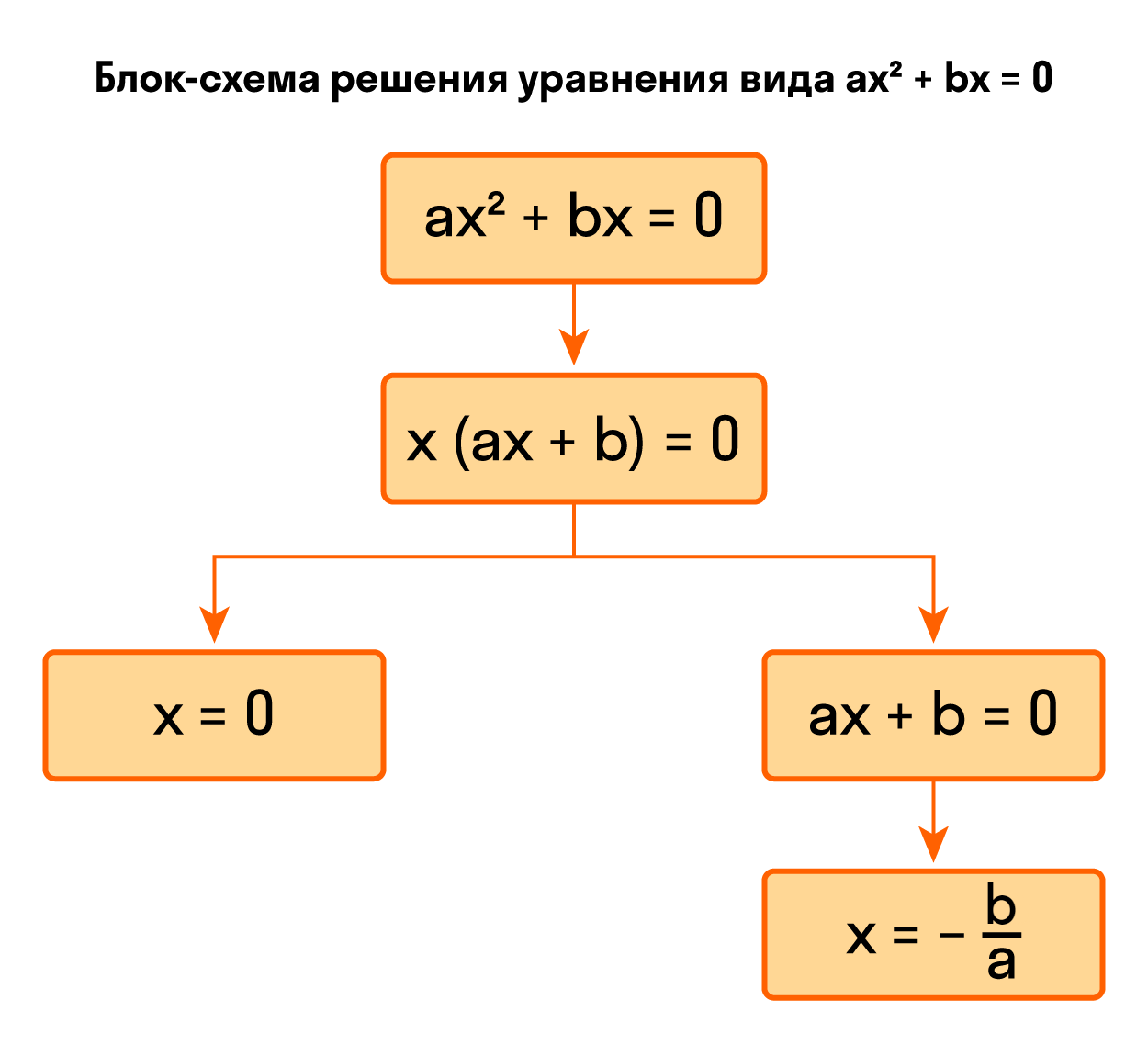
Разделим обе части на -1:

Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3.

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Как решить уравнение ax² + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника.

Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня: