Разделы: Математика
Класс: 10
«Уравнения будут существовать вечно».
Цели урока:
- Образовательные:
- углубление понимания методов решения тригонометрических уравнений;
- сформировать навыки различать, правильно отбирать способы решения тригонометрических уравнений.
- Воспитательные:
- воспитание познавательного интереса к учебному процессу;
- формирование умения анализировать поставленную задачу;
- способствовать улучшению психологического климата в классе.
- Развивающие:
- способствовать развитию навыка самостоятельного приобретения знаний;
- способствовать умению учащихся аргументировать свою точку зрения;
Оборудование: плакат с основными тригонометрическими формулами, компьютер, проектор, экран.
1 урок
I. Актуализация опорных знаний
Устно решить уравнения:
1) cosx = 1;
2) 2 cosx = 1;
3) cosx = –;
4) sin2x = 0;
5) sinx = –
6) sin
7) tgx =
8) cos 2 x – sin 2 x = 0
; 
; 
; 1) х = 2
2) х = ±
3) х =±
4) х =
5) х = (–1)
6) х = (–1)
7) х =
8) х =
+ 2
+ 2
II. Изучение нового материала
– Сегодня мы с вами рассмотрим более сложные тригонометрические уравнения. Рассмотрим 10 способов их решения. Далее будет два урока для закрепления, и на следующий урок будет проверочная работа. На стенде «К уроку» вывешены задания, аналогичные которым будут на проверочной работе, надо их прорешать до проверочной работы. (Накануне, перед проверочной работой, вывесить на стенде решения этих заданий).
Итак, переходим к рассмотрению способов решения тригонометрических уравнений. Одни из этих способов вам, наверное, покажутся трудными, а другие – лёгкими, т.к. некоторыми приёмами решения уравнений вы уже владеете.
Четверо учащихся класса получили индивидуальное задание: разобраться и показать вам 4 способа решения тригонометрических уравнений.
(Выступающие учащиеся заранее подготовили слайды. Остальные учащиеся класса записывают основные этапы решения уравнений в тетрадь.)
1 ученик: 1 способ. Решение уравнений разложением на множители
sin 4x = 3 cos 2x
Для решения уравнения воспользуемся формулой синуса двойного угла sin 2 
= 2 sin cos
2 sin 2x cos 2x – 3 cos 2x = 0,
cos 2x (2 sin 2x – 3) = 0. Произведение этих множителей равно нулю, если хотя бы один из множителей будет равен нулю.
2x = 
+ 
к, к 
Z или sin 2x = 1,5 – нет решений, т.к | sin| 
1
x = 
+ к; к Z.
Ответ: x = + к , к Z.
2 ученик. 2 способ. Решение уравнений преобразованием суммы или разности тригонометрических функций в произведение
cos 3x + sin 2x – sin 4x = 0.
Для решения уравнения воспользуемся формулой sin– sin 
= 2 sin 
сos
cos 3x + 2 sin 
сos 
= 0,
сos 3x – 2 sin x cos 3x = 0,
cos 3x (1 – 2 sinx) = 0. Полученное уравнение равносильно совокупности двух уравнений:
Множество решений второго уравнения полностью входит во множество решений первого уравнения. Значит 
Ответ:
3 ученик. 3 способ. Решение уравнений преобразованием произведения тригонометрических функций в сумму
sin 5x cos 3x = sin 6x cos2x.
Для решения уравнения воспользуемся формулой 
Ответ: 
4 ученик. 4 способ. Решение уравнений, сводящихся к квадратным уравнениям
3 sin x – 2 cos 2 x = 0,
3 sin x – 2 (1 – sin 2 x ) = 0,
2 sin 2 x + 3 sin x – 2 = 0,
Пусть sin x = t, где | t |
. Получим квадратное уравнение 2t 2 + 3t – 2 = 0,
. Таким образом 
. 
не удовлетворяет условию | t |.
Значит sin x = 
. Поэтому 
.
Ответ: 
III. Закрепление изученного по учебнику А. Н. Колмогорова
1. № 164 (а), 167 (а) (квадратное уравнение)
2. № 168 (а) (разложение на множители)
3. № 174 (а) (преобразование суммы в произведение)
4. 
(преобразование произведения в сумму)
(В конце урока показать решение этих уравнений на экране для проверки)
№ 164 (а)
2 sin 2 x + sin x – 1 = 0.
Пусть sin x = t, | t | 1. Тогда
2 t 2 + t – 1 = 0, t 
= – 1, t
= . Откуда 
Ответ: –
.
№ 167 (а)
3 tg 2 x + 2 tg x – 1 = 0.
Пусть tg x = 1, тогда получим уравнение 3 t 2 + 2 t – 1 = 0.
Ответ: 
№ 168 (а )
Ответ: 
№ 174 (а )
Ответ: 
Решить уравнение: 
Ответ: 
2 урок (урок-лекция)
IV. Изучение нового материала (продолжение)
– Итак, продолжим изучение способов решения тригонометрических уравнений.
5 способ. Решение однородных тригонометрических уравнений
Уравнения вида a sin x + b cos x = 0, где a и b – некоторые числа, называются однородными уравнениями первой степени относительно sin x или cos x.
sin x – cos x = 0. Разделим обе части уравнения на cos x. Так можно сделать, потери корня не произойдёт, т.к. , если cos x = 0, то sin x = 0. Но это противоречит основному тригонометрическому тождеству sin 2 x + cos 2 x = 1.
Получим tg x – 1 = 0.
Ответ: 
Уравнения вида a sin 2 x + bcos 2 x + c sin x cos x = 0 , где a, b, c –некоторые числа, называются однородными уравнениями второй степени относительно sin x или cos x.
sin 2 x – 3 sin x cos x + 2 cos 2 = 0. Разделим обе части уравнения на cos x, при этом потери корня не произойдёт, т.к. cos x = 0 не является корнем данного уравнения.
tg 2 x – 3tg x + 2 = 0.
Пусть tg x = t. D = 9 – 8 = 1.
тогда 
Отсюда tg x = 2 или tg x = 1.
В итоге x = arctg 2 + 
, x = 
Ответ: arctg 2 + ,
Рассмотрим ещё одно уравнение: 3 sin 2 x – 3 sin x cos x + 4 cos 2 x = 2.
Преобразуем правую часть уравнения в виде 2 = 2 · 1 = 2 · (sin 2 x + cos 2 x). Тогда получим:
3sin 2 x – 3sin x cos x + 4cos 2 x = 2 · (sin 2 x + cos 2 x),
3sin 2 x – 3sin x cos x + 4cos 2 x – 2sin 2 x – 2 cos 2 x = 0,
sin 2 x – 3sin x cos x + 2cos 2 x = 0. (Получили 2 уравнение, которое уже разобрали).
Ответ: arctg 2 + k,
6 способ. Решение линейных тригонометрических уравнений
Линейным тригонометрическим уравнением называется уравнение вида a sin x + b cos x = с, где a, b, c – некоторые числа.
Рассмотрим уравнение sin x + cos x = – 1.
Перепишем уравнение в виде: 
Учитывая, что 
и
, получим:
Ответ: 
7 способ. Введение дополнительного аргумента
Выражение a cos x + b sin x можно преобразовать:
.
(это преобразование мы уже ранее использовали при упрощении тригонометрических выражений)
Введём дополнительный аргумент – угол 
такой, что 
Тогда 
Рассмотрим уравнение: 3 sinx + 4 cosx = 1.
Учтём, что 
. Тогда получим 
0,6 sin x + 0,8 cosx = 1. Введём дополнительный аргумент – угол такой, что 
, т.е. = arcsin 0,6. Далее получим 
Ответ: – arcsin 0,8 + +
8 способ. Уравнения вида Р 
Такого рода уравнения удобно решать при помощи введения вспомогательной переменной t = sin x ± cosx. Тогда 1 ± 2 sinx cosx = t 2 .
Решить уравнение: sinx + cosx + 4 sinx cosx – 1 = 0.
Введём новую переменную t = sinx + cosx, тогда t 2 = sin 2 x + 2sin x cos x + cos 2 = 1 + 2 sin x cos x Откуда sin x cos x = 
. Следовательно получим:
t + 2 (t 2 – 1) – 1 = 0.
2 t 2 + t – 2 – 1 = 0,
2 t 2 + t – 3 = 0..Решив уравнение, получим 
= 1, 
=
.
sinx + cosx = 1 или sinx + cosx =
Ответ: 
9 способ. Решение уравнений, содержащих тригонометрические функции под знаком радикала.
Решить уравнение: 
В соответствии с общим правилом решения иррациональных уравнений вида
, запишем систему, равносильную исходному уравнению:
Решим уравнение 1 – cos x = 1 – cos 2 x.
1 – cos x = 1 – cos 2 x,
1 – cos x – (1 – cos x) (1 + cos x) = 0,
(1 – cos x) (1 – 1 – cos x) = 0,
– (1 – cos x) cos x = 0.
Условию 
удовлетворяют только решения
Ответ: 
10 способ. Решение уравнений с использованием ограниченности тригонометрических функций y = sin x и y = cos x.
Решить уравнение: sin x + sin 9x = 2.
Так как при любых значениях х sin x 1, то данное уравнение равносильно системе: 
Решение системы 
Ответ:
V. Итог урока
Таким образом мы сегодня рассмотрели 10 различных способов решения тригонометрических уравнений. Безусловно, многие из приведённых задач могут быть решены несколькими способами.
(Пятерым наиболее подготовленным учащимся , а также всем желающим дать индивидуальное творческое задание: найти различные способы решения тригонометрического уравнения sinx + cosx = 1 )
Домашнее задание: № 164 -170 (в, г).
Видео:10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать
Тригонометрические уравнения
Решение простейших тригонометрических уравнений
Градусы и радианы
Знакомство с тригонометрической окружностью
Повороты на тригонометрической окружности
Как много боли связано со словом тригонометрия. Эта тема появляется в 9 классе и уже никуда не исчезает. Тяжело приходится тем, кто чего-то не понял сразу. Попробуем это исправить, чтобы осветить ваше лицо улыбкой при слове тригонометрия или хотя бы добиться «poker face».
Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах .
1 радиан = 180/π ≈ 57,3 градусов
Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа π.
Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на π!
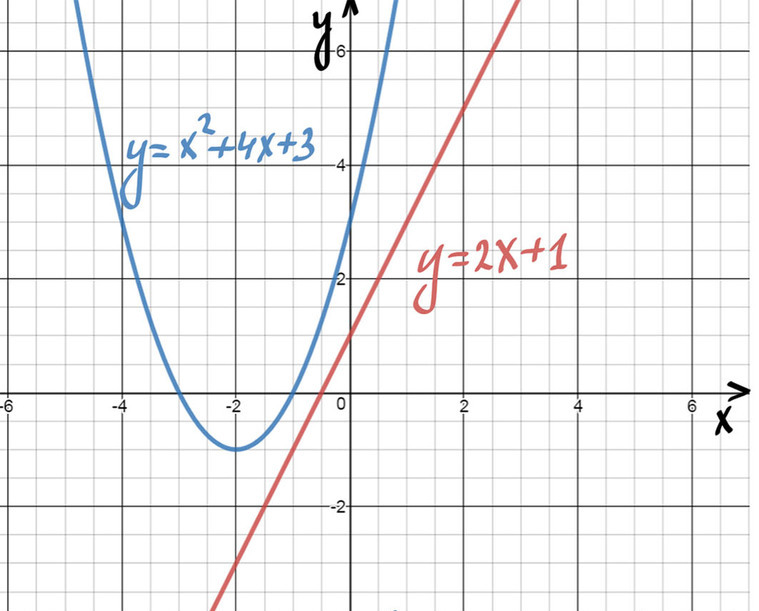
О графиках синуса, косинуса и тангеса поговорим в другой статье.
А сейчас начем с декартовой (прямоугольной) системы координат.
Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.
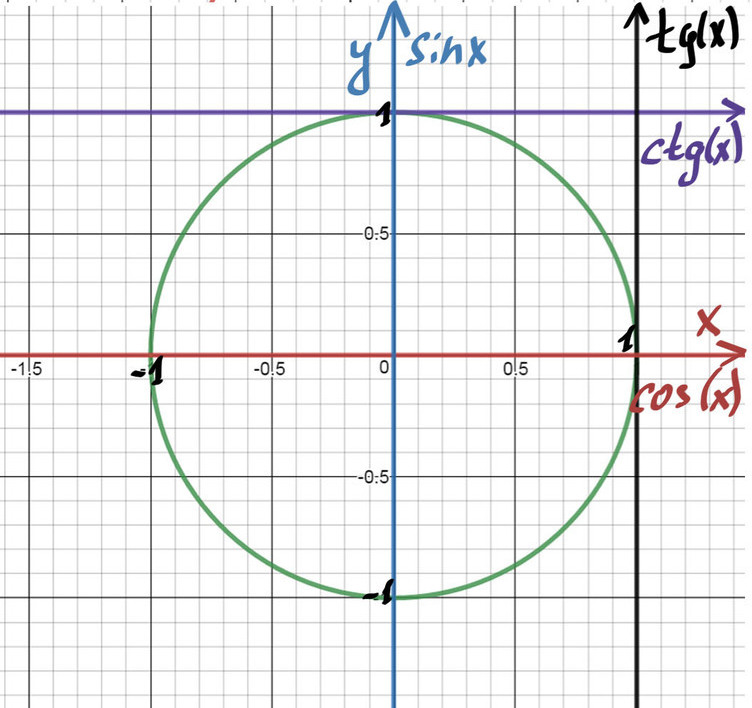
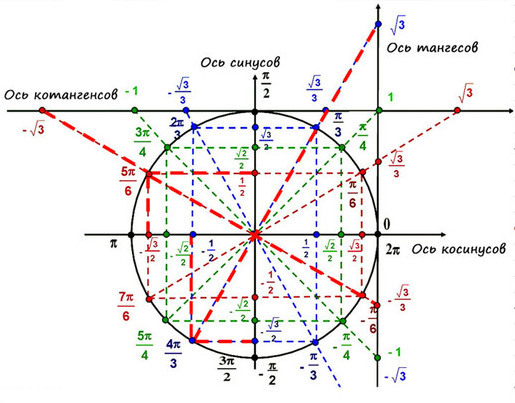
На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:
Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.
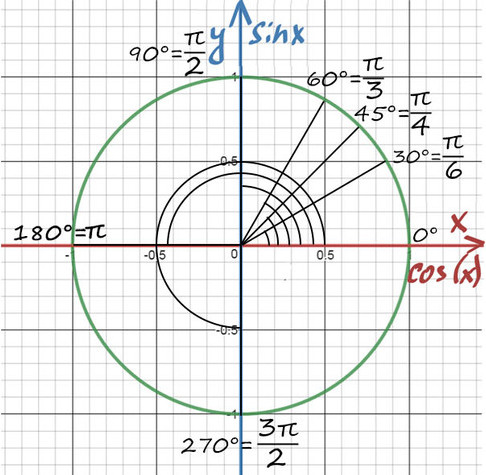
А теперь отметим основные значения градусов и радиан на окружности.
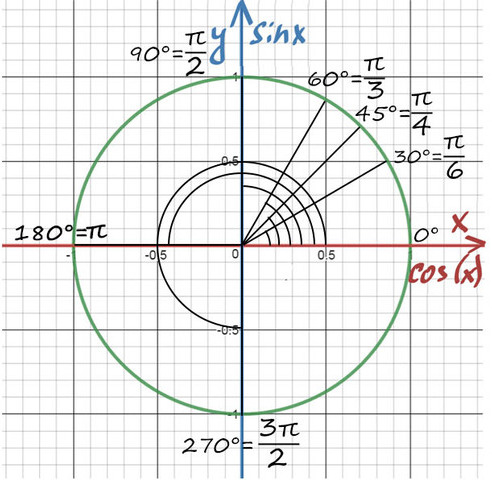
Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.
Достаточно запомнить, что π = 180° (тогда π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).
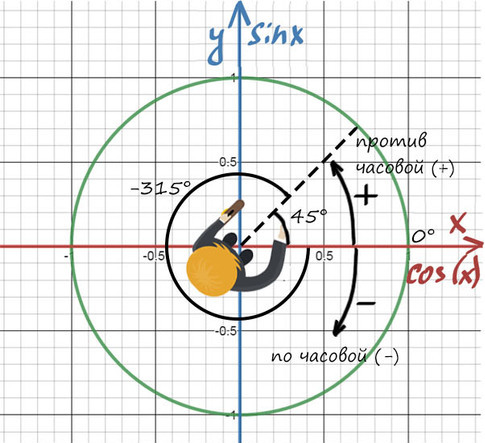
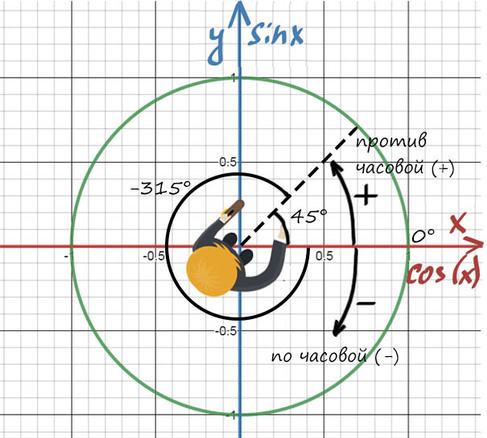
А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):
От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).
Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).
Главное — направление, куда мы будем смотреть, а не угол!
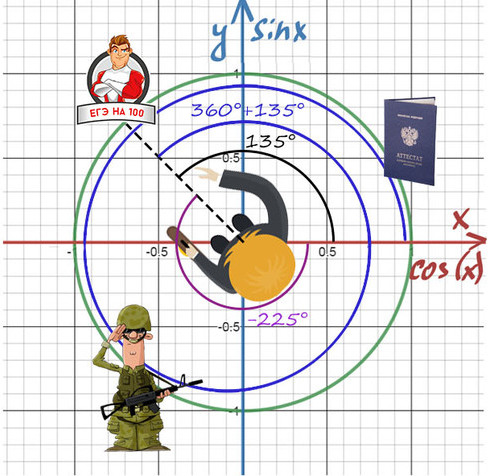
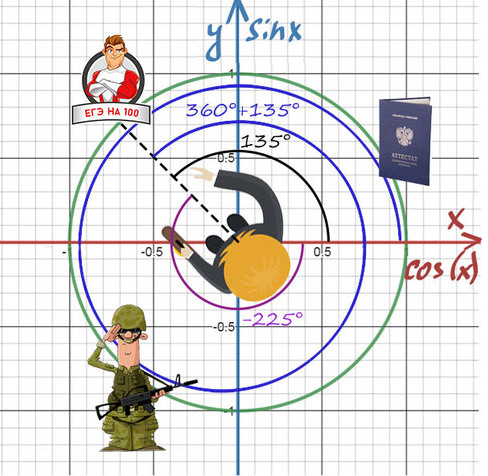
Нужно направить пунктир на 100 баллов, а сколько оборотов и в какую сторону вокруг себя мы сделаем — без разницы!
Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°.
А теперь у тебя есть два пути:
Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:
А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.
Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.
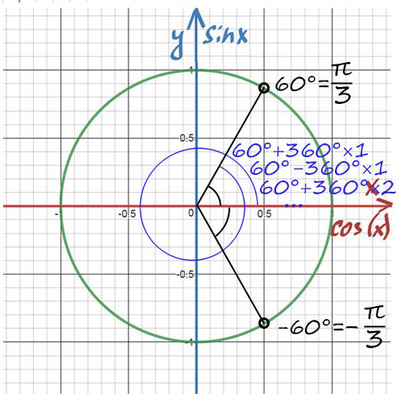
Сразу попробуем разобрать на примере:
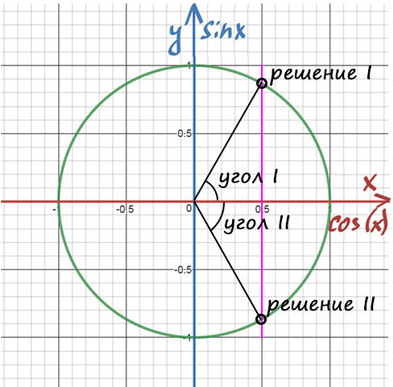
1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение ½ и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.
2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.
Дело за малым — найти эти углы.
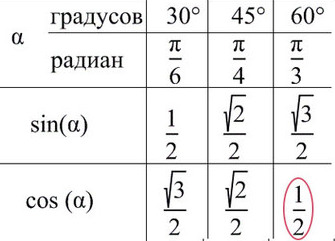
Лучше обойтись «малой кровью» и выучить значение синуса и косинуса для углов от 30° до 60°.
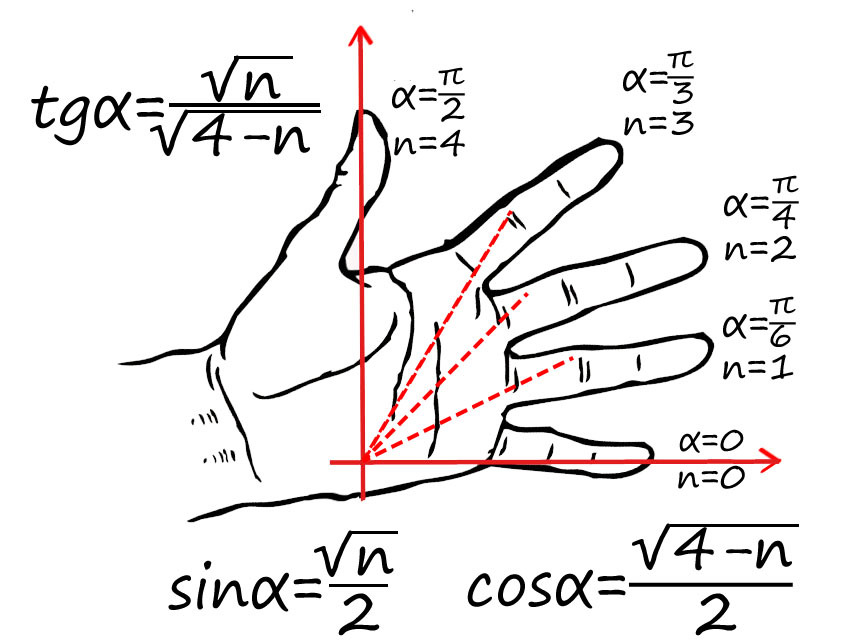
Или запомнить такой прием:
Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).
Например, требуется найти sin(π/2) : π/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.
cos(π/4) — ? π/4 соответсвует среднему пальцу (n = 2) => cos(π/4) = √2/2.
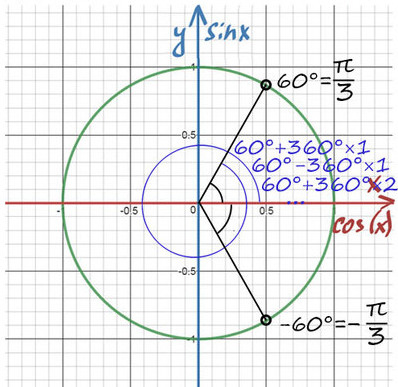
При значении cos(x) = ½ из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +π/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).
Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (−). x = −π/3 (угол показан нижней черной дугой).
И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:
Когда требуется попасть в «100 баллов», мы можем в них попасть с помощью поворота на . =-225°=135°=495°=.
То же самое и здесь! Разные углы могут отражать одно и то же направление.
Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2π (синим цветом) сколько угодно раз и в любом направлении.
Таким образом, попасть в первое направление 60° можно: . 60°-360°, 60°, 60°+360°.
И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть☻)
Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n∈Ζ) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = −60 + 360n.
Но мы же договорились, что на окружности все записывают через π, поэтому cos(x) = ½ при x = π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.
Ответ: x = π/3 + 2πn, x= − π/3 + 2πk, (n, k) ∈Ζ.
Пример №2. 2sinx = √2
Первое, что следует сделать, это перенести 2-ку вправо => sinx=√2/2
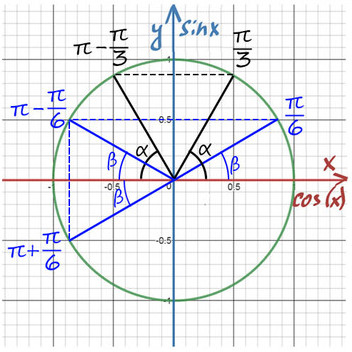
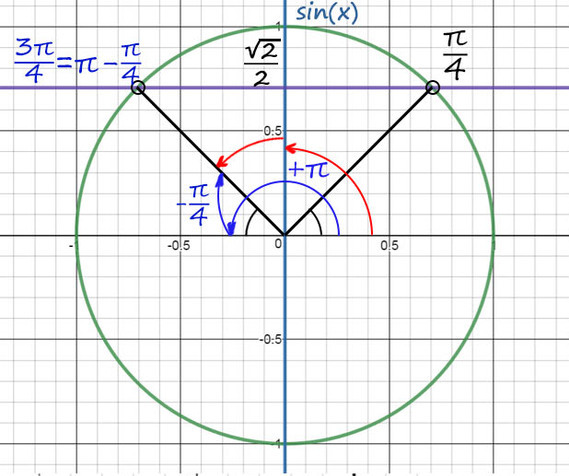
1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем √2/2 и проводим ⊥ фиолетовую прямую до пересечений с окружностью.
2) Из таблицы sinx = √2/2 при х = π/4, а вторую точку будем искать с помощью поворота до π, а затем нужно вернуться обратно на π/4.
Поэтому вторая точка будет x = π − π/4 = 3π/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.
И еще не забудем добавить +2πn, n∈Ζ.
Ответ: 3π/4 + 2πn и π/4 + 2πk, k и n − любые целые числа.
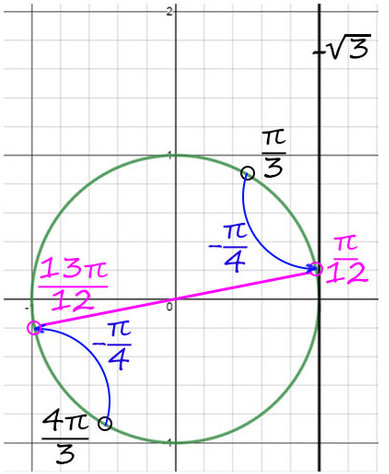
Пример №3. tg(x + π/4) = √3
Вроде все верно, тангенс равняется числу, но смущает π/4 в тангенсе. Тогда сделаем замену: y = x + π/4.
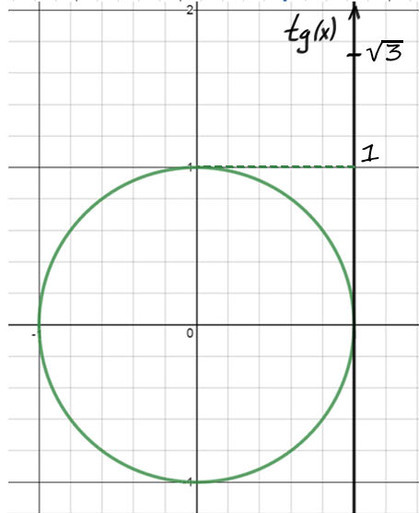
tg(y) = √3 выглядит уже не так страшно. Вспомним, где ось тангенсов.
1) А теперь на оси тангенсов отметим значение √3, это выше чем 1.
2) Проведем фиолетовую прямую через значение √3 и начало координат. Опять на пересечении с окружностью получается 2 точки.
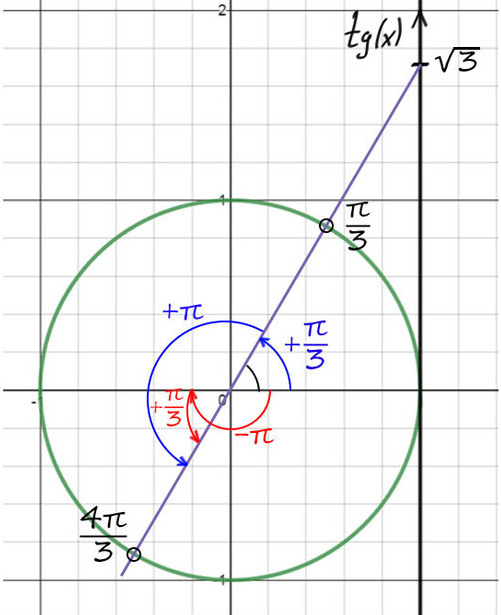
По мнемоническому правилу при тангенсе √3 первое значение — это π/3.
3) Чтобы попасть во вторую точку, можно к первой точке (π/3) прибавить π => y = π/3 + π = 4π/3.
4) Но мы нашли только y , вернемся к х. y = π/3 + 2πn и y = x + π/4, тогда x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Ζ.
Второй корень: y = 4π/3 + 2πk и y = x + π/4, тогда x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.
Теперь корни на окружности будут здесь:
Ответ: π/12 + 2πn и 13π/12 + 2πk, k и n — любые целые числа.
Конечно, эти два ответа можно объединить в один. От 0 поворот на π/12, а дальше каждый корень будет повторяться через каждый π (180°).
Ответ можно записать и так: π/12 + πn, n∈Ζ.
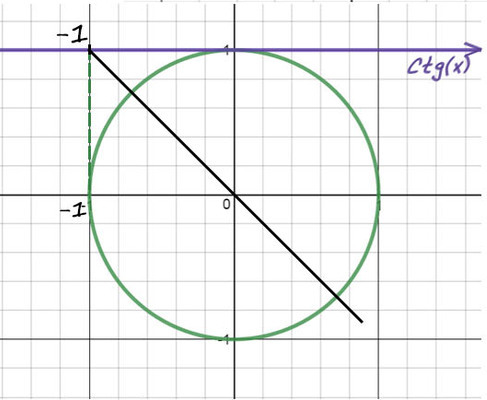
Пример №4: −10ctg(x) = 10
Перенесем (−10) в другую часть: ctg(x) = −1. Отметим значение -1 на оси котангенсов.
1) Проведем прямую через эту точку и начало координат.
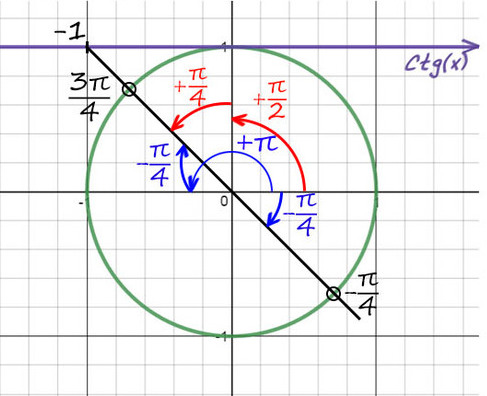
2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при π/4). Но здесь −1, поэтому одна точка будет −π/4. А вторую найдем поворотом до π, а потом назад на π/4 (π − π/4).
Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (π, 2π, 3π. ) так намного меньше шансов запутаться.
Не забываем добавить к каждой точке 2πk.
Ответ: 3π/4 + 2πn и −π/4 + 2πk, k и n — любые целые числа.
Алгоритм решения тригонометрических уравнений (на примере cos(x) = − √ 3/2) :
- Отмечаем значение (−√3/2) на оси тригонометрической функции (косинусов, это ось Х).
- Проводим перпендикулярную прямую оси (косинусов) до пересечений с окружностью.
- Точки пересечения с окружностью и будут являться корнями уравнения.
- Значение одной точки (без разницы, как в нее попадете) +2πk.
Азов достаточно, прежде чем идти дальше закрепите полученные знания.
Видео:Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать
Тригонометрические уравнения. Как решать тригонометрические уравнения?
Тригонометрические уравнения – уравнения, содержащие переменную под знаком тригонометрических функций.
Если проще: это уравнения, в которых неизвестные (иксы) или выражения с ними находятся внутри синусов , косинусов , тангенсов и котангенсов .
Видео:Тригонометрическая окружность. Как выучить?Скачать
Как решать тригонометрические уравнения:
Любое тригонометрическое уравнение нужно стремиться свести к одному из видов:
где (t) – выражение с иксом, (a) – число. Такие тригонометрические уравнения называются простейшими. Их легко решать с помощью числовой окружности ( тригонометрического круга ) или специальных формул:
(sin x=a) (⇔) ( left[ beginx=arcsin a+2πn, n∈Z\ x=π-arcsin a+2πl, l∈Zendright.)
если (a∈[-1;1])
Инфографику о решении простейших тригонометрических уравнений смотри здесь: (sinx=a) , (cosx=a) , (tgx=a) и (ctgx=a) .
Пример. Решите тригонометрическое уравнение (sinx=-)(frac).
Решение:
Ответ: (x=) (frac) (+πk), (k∈Z).
Пример. Решите тригонометрическое уравнение (cos(3x+frac)=0).
Решение:
Ответ: (x=) (frac) (+) (frac) (x=-) (frac) (+) (frac) , (k∈Z).
Сводить тригонометрические уравнения к простейшим – задача творческая, тут нужно использовать и тригонометрические формулы , и особые методы решений уравнений:
— Метод введения новой переменной (самый популярный в ЕГЭ).
— Метод разложения на множители .
— Метод вспомогательных аргументов.
Рассмотрим пример решения квадратно-тригонометрического уравнения
Пример. Решите тригонометрическое уравнение (2cos^2x-5cosx+2=0)
Решение:
 |
Ответ: (x=±) (frac) (+2πk), (k∈Z).
Пример решения тригонометрического уравнения с исследованием ОДЗ:
Пример(ЕГЭ). Решите тригонометрическое уравнение (frac<2cos^2x-sin>) (=0)
